华东师大版七年级数学上册3.3.1单项式课件(20张ppt)
文档属性
| 名称 | 华东师大版七年级数学上册3.3.1单项式课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 344.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 13:48:57 | ||
图片预览








文档简介
(共20张PPT)
单
项
式
理解单项式及一个单项式的系数、次数的概念;
能够熟练地确定一个单项式的系数和次数;
会用单项式表示简单的数量关系。
学习目标
掌握单项式及系数、次数的概念。
重点
会用单项式表示简单的数量关系。
难点
重难点
回顾
(1)若正方形的边长为
a
,则正方形的面积是___________.
(2)若三角形的一边长为
a
,这边上的高为
h
,则这个三角形的面积为__________.
(3)若
m
表示一个有理数,则它的相反数是_________.
(4)小馨每月从零花钱中拿出
x
元钱捐给希望工程,一年下来小馨共捐款_________元.
列出的代数式都有什么共同特点?
上面列出的代数式都是由数与字母的乘积组成的,这样的式子叫做单项式。
单独的一个数或一个字母也是单项式。
例如:等都是单项式。
注意:像等不是单项式,它们不是数与字母的乘积组成的。
单项式
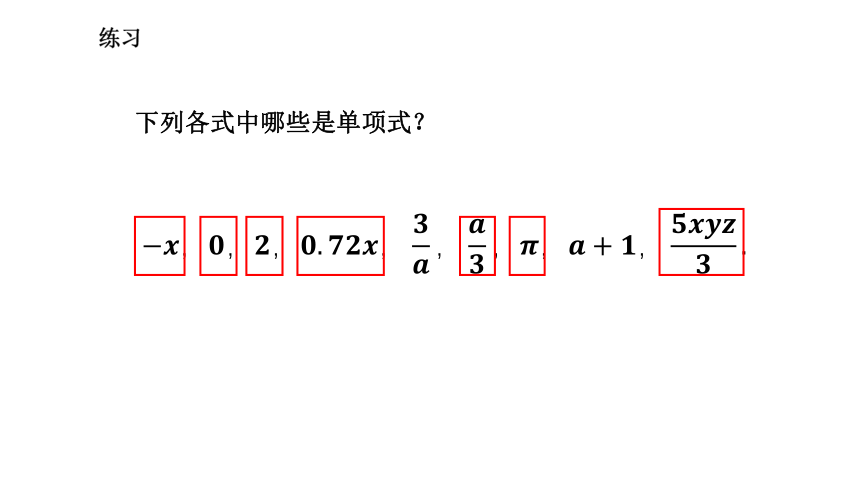
下列各式中哪些是单项式?
练习
1、单独一个数或一个字母也是单项式.
2、不含加减运算,单项式只含有乘积运算.
3、单项式数字因数与字母可能一个或多个.
判断单项式的方法
4、可以含有除以数的运算,但不能含有除以字母的运算.
小结
例如,单项式
、
a?、
的系数分别是、
1、.
单项式中的数字因数叫做这个单项式的系数.
需要注意的是,当字母前面没有数字因数时,单项式的系数是1或-1
系数
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如,在单项式的次数是2;的次数是4;的次数是1.
需要注意的是,单个字母的系数是
1
次数
单项式的次数是几,就称其为几次单项式。
如:我们称为二次单项式.
系数:
数字因数,
不要忽略负号;
π是具体的数。
指数
1
1
所有指数的和就是次数.
小结
判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它的系数与次数.
(1)不是单项式,因为代数式中出现了加法运算.
(2)是单项式,它的系数是,次数是3.
例1
单项式
5a2
mn
系数
次数
1.
填表:
随堂练习
判断下列说法是否正确,如果不正确,请说明理由.
(1)单项式
m
既没有系数,也没有次数;
(2)单项式
的系数是5.
不正确,单项式
m
的系数是1,次数也是1.
不正确,单项式
的数字因数是,所以它的系数是.
随堂练习
若是关于
x,y
的一个三次单项式,m,n应满足的条件?
解:单项式的系数是
,次数是
.
要使得是关于
x,y
的三次单项式,
且
即:且
若,此时整体就是0,就不是三次单项式了.
例
基础巩固
1.
下列式子中:中,单项式的个数是(
)
A.1个
B.2个
C.3个
D.4个
2.
单项式
的系数是__________,次数是__________.
3.
单项式的系数是__________,次数是__________.
C
6
6
基础巩固
4.
观察下面的单项式:
a,2a2,4a3,8a4,……,根据你发现的规律,第八个式子是________.
5.
按照一定规律排列的单项式:
x,-2x2,3a3,-4a4,
5a5,
-6a6,
……,第n个单项式是(
)
A.
B.
D.
C.
C
128a8
6.
判断下列说法是否正确:
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是.
(
)
基础巩固
7.若
ax2yb-1
是关于x、y的单项式,系数为6,次数是3,则a=_____,b=________.
8.若
|m-3|
x3yn+1
是关于x、y的单项式,系数为5,次数是4,则m=_________,n=________.
6
2
8或-2
0
基础巩固
单项式
单项式概念
单项式的系数和次数
知识
考点
求一个单项式的系数和次数
课堂总结
单
项
式
理解单项式及一个单项式的系数、次数的概念;
能够熟练地确定一个单项式的系数和次数;
会用单项式表示简单的数量关系。
学习目标
掌握单项式及系数、次数的概念。
重点
会用单项式表示简单的数量关系。
难点
重难点
回顾
(1)若正方形的边长为
a
,则正方形的面积是___________.
(2)若三角形的一边长为
a
,这边上的高为
h
,则这个三角形的面积为__________.
(3)若
m
表示一个有理数,则它的相反数是_________.
(4)小馨每月从零花钱中拿出
x
元钱捐给希望工程,一年下来小馨共捐款_________元.
列出的代数式都有什么共同特点?
上面列出的代数式都是由数与字母的乘积组成的,这样的式子叫做单项式。
单独的一个数或一个字母也是单项式。
例如:等都是单项式。
注意:像等不是单项式,它们不是数与字母的乘积组成的。
单项式
下列各式中哪些是单项式?
练习
1、单独一个数或一个字母也是单项式.
2、不含加减运算,单项式只含有乘积运算.
3、单项式数字因数与字母可能一个或多个.
判断单项式的方法
4、可以含有除以数的运算,但不能含有除以字母的运算.
小结
例如,单项式
、
a?、
的系数分别是、
1、.
单项式中的数字因数叫做这个单项式的系数.
需要注意的是,当字母前面没有数字因数时,单项式的系数是1或-1
系数
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如,在单项式的次数是2;的次数是4;的次数是1.
需要注意的是,单个字母的系数是
1
次数
单项式的次数是几,就称其为几次单项式。
如:我们称为二次单项式.
系数:
数字因数,
不要忽略负号;
π是具体的数。
指数
1
1
所有指数的和就是次数.
小结
判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它的系数与次数.
(1)不是单项式,因为代数式中出现了加法运算.
(2)是单项式,它的系数是,次数是3.
例1
单项式
5a2
mn
系数
次数
1.
填表:
随堂练习
判断下列说法是否正确,如果不正确,请说明理由.
(1)单项式
m
既没有系数,也没有次数;
(2)单项式
的系数是5.
不正确,单项式
m
的系数是1,次数也是1.
不正确,单项式
的数字因数是,所以它的系数是.
随堂练习
若是关于
x,y
的一个三次单项式,m,n应满足的条件?
解:单项式的系数是
,次数是
.
要使得是关于
x,y
的三次单项式,
且
即:且
若,此时整体就是0,就不是三次单项式了.
例
基础巩固
1.
下列式子中:中,单项式的个数是(
)
A.1个
B.2个
C.3个
D.4个
2.
单项式
的系数是__________,次数是__________.
3.
单项式的系数是__________,次数是__________.
C
6
6
基础巩固
4.
观察下面的单项式:
a,2a2,4a3,8a4,……,根据你发现的规律,第八个式子是________.
5.
按照一定规律排列的单项式:
x,-2x2,3a3,-4a4,
5a5,
-6a6,
……,第n个单项式是(
)
A.
B.
D.
C.
C
128a8
6.
判断下列说法是否正确:
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是.
(
)
基础巩固
7.若
ax2yb-1
是关于x、y的单项式,系数为6,次数是3,则a=_____,b=________.
8.若
|m-3|
x3yn+1
是关于x、y的单项式,系数为5,次数是4,则m=_________,n=________.
6
2
8或-2
0
基础巩固
单项式
单项式概念
单项式的系数和次数
知识
考点
求一个单项式的系数和次数
课堂总结
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
