人教版七年级数学上册-1.3.2.1《有理数的减法》导学案(无答案)
文档属性
| 名称 | 人教版七年级数学上册-1.3.2.1《有理数的减法》导学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 39.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 14:42:05 | ||
图片预览

文档简介
1.3.2.1
有理数的减法
导学案
【学习目标】
1、理解有理数减法法则,能熟练进行减法运算.
2、有理数减法法则的理解和运用.
3、会将减法转化为加法,进行加减混合运算,体会化归思想.
【知识回顾】
有理数的加法法则:
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
加法交换律:
加法结合律:
(1)
14
+
16
=
(2)(–13)+(–27)
=
(3)(–19)+
20
=
(4)
43
+(–50)
=
(5)(–56)+
56
=
(6)
106
+
0
=
(7)
0
+(–2017)
=
【教学过程】
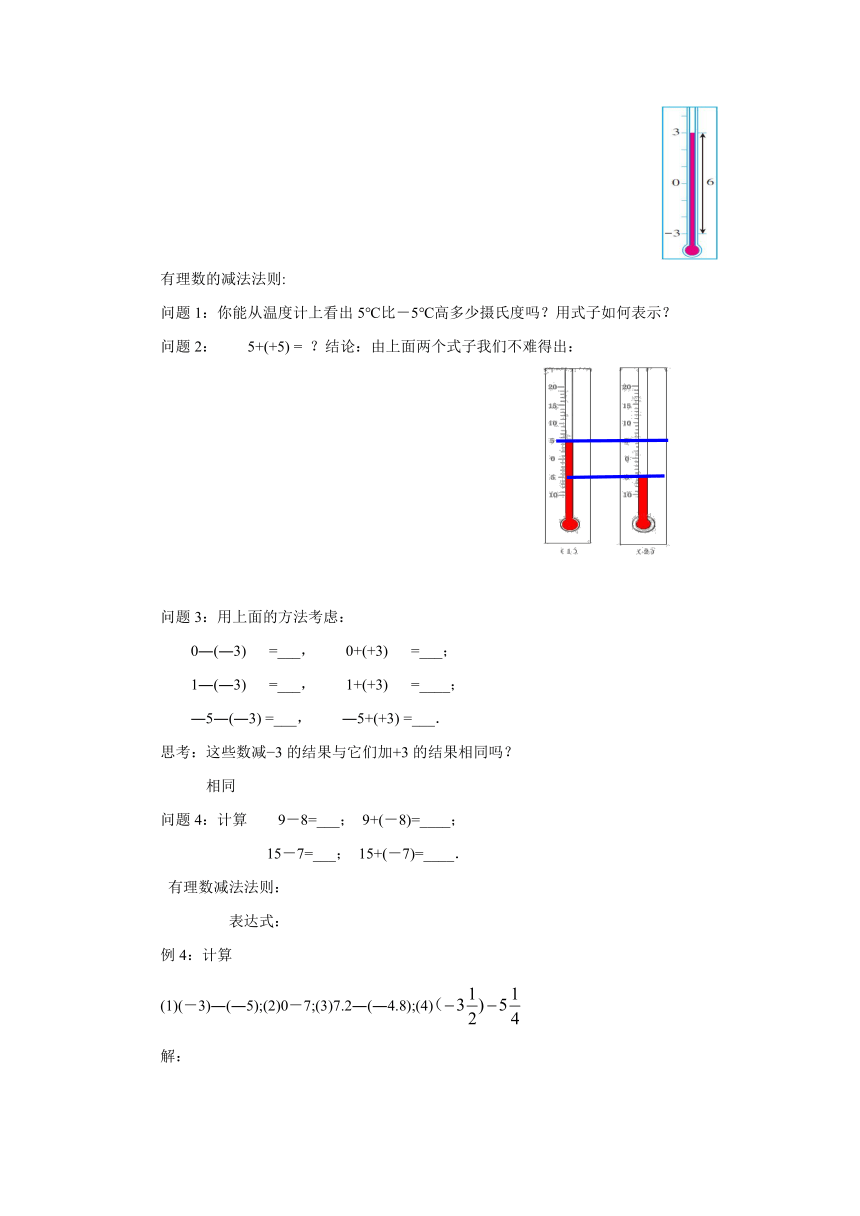
实际问题中有时还要涉及有理数的减法.
例如,本章引言中,北京某天的气温是-
3
℃?3
℃,这天的温差(最高气温减最低气温,单位:℃)就是3
–(-3).这里遇到正数与负数的减法.
如图,你能看出3℃比-
3
℃高多少摄氏度吗?
有理数的减法法则:
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2:
5+(+5)
=
?结论:由上面两个式子我们不难得出:
问题3:用上面的方法考虑:
0―(―3)
=___,
0+(+3)
=___;
1―(―3)
=___,
1+(+3)
=____;
―5―(―3)
=___,
―5+(+3)
=___.
思考:这些数减?3的结果与它们加+3的结果相同吗?
相同
问题4:计算
9-8=___;
9+(-8)=____;
15-7=___;
15+(-7)=____.
有理数减法法则:
表达式:
例4:计算
(1)(-3)―(―5);(2)0-7;(3)7.2―(―4.8);(4)
解:
【当堂练习】
填空:(1)-4-(-3.2)=
-4+
=
;
(2)(-35)-(+12)=
.
2.计算(口答):
(1)6-9;
(2)(+4)-(-7);
(3)(-5)-(-8)
;
(4)(-4)-9;
(5)0-(-5);
?
(6)0-5.
有理数减法与小学里学过的减法的不同点:
(1)被减数可以小于减数.
如:
1-5 ;
(2)差可以大于被减数,
如:(+3)-(-2)=5;
(3)大数减小数,差为正数;小数减大数,差为负数.
3、判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大(
)
(2)两个数相减,被减数一定比减数大(
)
(3)两数之差一定小于被减数(
)
(4)0减去任何数,差都为负数(
)
(5)较大的数减去较小的数,差一定是正数(
)
4、计算:
(1)比2?C
低
8?C
的温度;
(2)比-3?C
低
6?C
的温度.
解:
5、
计算:
(1)
3-(-2)
;
(2)
(-1)-(+2)
;
(3)
1-5
;
(4)
(-1.3)-2.6
;
(5)
0-9
;
解:
6、世界上最高的山峰是珠穆朗玛峰,其海拔高度是
8844
米,吐鲁番盆地的海拔高度是–155
米,两处高度相差多少米?
7、
世界上最大的咸水湖是位于亚洲西部的死海,湖面海拔高度为-392米.我国最大的咸水湖是位于西部的青海湖,湖面海拔高度为3195米,这两个咸水湖的湖面高度相差多少?
【学习疑问】
1.哪个环节没弄清楚?
2.有什么困惑?
有理数的减法
导学案
【学习目标】
1、理解有理数减法法则,能熟练进行减法运算.
2、有理数减法法则的理解和运用.
3、会将减法转化为加法,进行加减混合运算,体会化归思想.
【知识回顾】
有理数的加法法则:
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
加法交换律:
加法结合律:
(1)
14
+
16
=
(2)(–13)+(–27)
=
(3)(–19)+
20
=
(4)
43
+(–50)
=
(5)(–56)+
56
=
(6)
106
+
0
=
(7)
0
+(–2017)
=
【教学过程】
实际问题中有时还要涉及有理数的减法.
例如,本章引言中,北京某天的气温是-
3
℃?3
℃,这天的温差(最高气温减最低气温,单位:℃)就是3
–(-3).这里遇到正数与负数的减法.
如图,你能看出3℃比-
3
℃高多少摄氏度吗?
有理数的减法法则:
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2:
5+(+5)
=
?结论:由上面两个式子我们不难得出:
问题3:用上面的方法考虑:
0―(―3)
=___,
0+(+3)
=___;
1―(―3)
=___,
1+(+3)
=____;
―5―(―3)
=___,
―5+(+3)
=___.
思考:这些数减?3的结果与它们加+3的结果相同吗?
相同
问题4:计算
9-8=___;
9+(-8)=____;
15-7=___;
15+(-7)=____.
有理数减法法则:
表达式:
例4:计算
(1)(-3)―(―5);(2)0-7;(3)7.2―(―4.8);(4)
解:
【当堂练习】
填空:(1)-4-(-3.2)=
-4+
=
;
(2)(-35)-(+12)=
.
2.计算(口答):
(1)6-9;
(2)(+4)-(-7);
(3)(-5)-(-8)
;
(4)(-4)-9;
(5)0-(-5);
?
(6)0-5.
有理数减法与小学里学过的减法的不同点:
(1)被减数可以小于减数.
如:
1-5 ;
(2)差可以大于被减数,
如:(+3)-(-2)=5;
(3)大数减小数,差为正数;小数减大数,差为负数.
3、判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大(
)
(2)两个数相减,被减数一定比减数大(
)
(3)两数之差一定小于被减数(
)
(4)0减去任何数,差都为负数(
)
(5)较大的数减去较小的数,差一定是正数(
)
4、计算:
(1)比2?C
低
8?C
的温度;
(2)比-3?C
低
6?C
的温度.
解:
5、
计算:
(1)
3-(-2)
;
(2)
(-1)-(+2)
;
(3)
1-5
;
(4)
(-1.3)-2.6
;
(5)
0-9
;
解:
6、世界上最高的山峰是珠穆朗玛峰,其海拔高度是
8844
米,吐鲁番盆地的海拔高度是–155
米,两处高度相差多少米?
7、
世界上最大的咸水湖是位于亚洲西部的死海,湖面海拔高度为-392米.我国最大的咸水湖是位于西部的青海湖,湖面海拔高度为3195米,这两个咸水湖的湖面高度相差多少?
【学习疑问】
1.哪个环节没弄清楚?
2.有什么困惑?
