12.1全等三角形同步能力提升训练 2021-2022学年八年级数学人教版上册(word版含解析)
文档属性
| 名称 | 12.1全等三角形同步能力提升训练 2021-2022学年八年级数学人教版上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 20:22:14 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学上册《12.1全等三角形》同步能力提升训练(附答案)
一、选择题
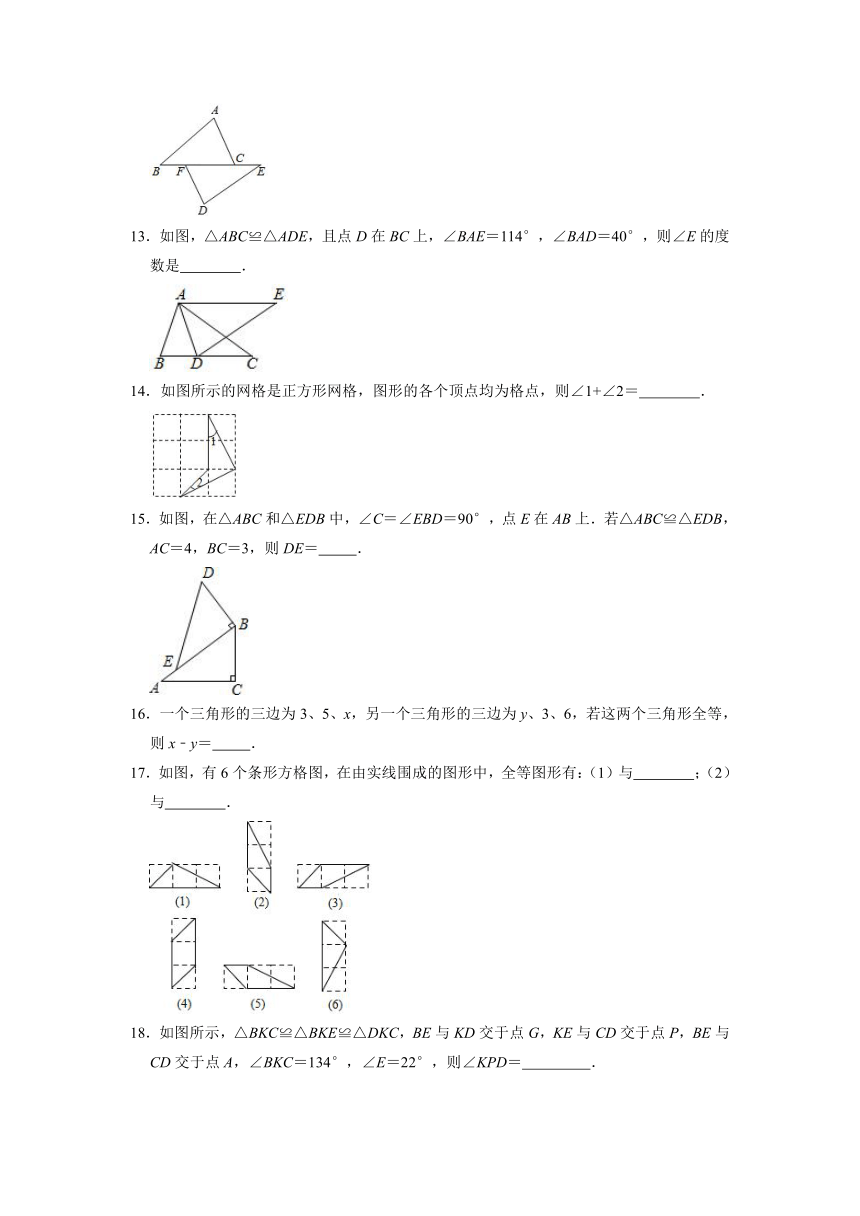
1.下列四个选项中的图形与下面的图形全等的是( )
A.B.C.D.
2.在下列每组图形中,是全等形的是( )
A.
B.
C.
D.
3.已知△ABC≌△A′B′C′,∠A=80°,∠B=40°,那么∠C′的度数为( )
A.80°
B.40°
C.60°
D.120°
4.如图△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30°
B.35°
C.40°
D.50°
5.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
6.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
7.如图所示,点B、E、C、F在一条直线上,△ABC≌△DEF,则下列结论正确的是( )
A.AB∥DE,但AC不平行于DF
B.BE=EC=CF
C.AC∥DF,但AB不平行于DE
D.AB∥DE,AC∥DF
8.图中的两个三角形全等,则∠1等于( )
A.45°
B.62°
C.73°
D.135°
9.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
10.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30
B.27
C.35
D.40
二、填空题
11.如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是
°.
12.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
13.如图,△ABC≌△ADE,且点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是
.
14.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
15.如图,在△ABC和△EDB中,∠C=∠EBD=90°,点E在AB上.若△ABC≌△EDB,AC=4,BC=3,则DE=
.
16.一个三角形的三边为3、5、x,另一个三角形的三边为y、3、6,若这两个三角形全等,则x﹣y=
.
17.如图,有6个条形方格图,在由实线围成的图形中,全等图形有:(1)与
;(2)与
.
18.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
三、解答题
19.如图,请沿图中的虚线,用三种方法将下列图形划分为两个全等图形.
20.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
21.如图,△ABC≌△ADE,点E在边BC上,求证:∠BED=∠BAD.
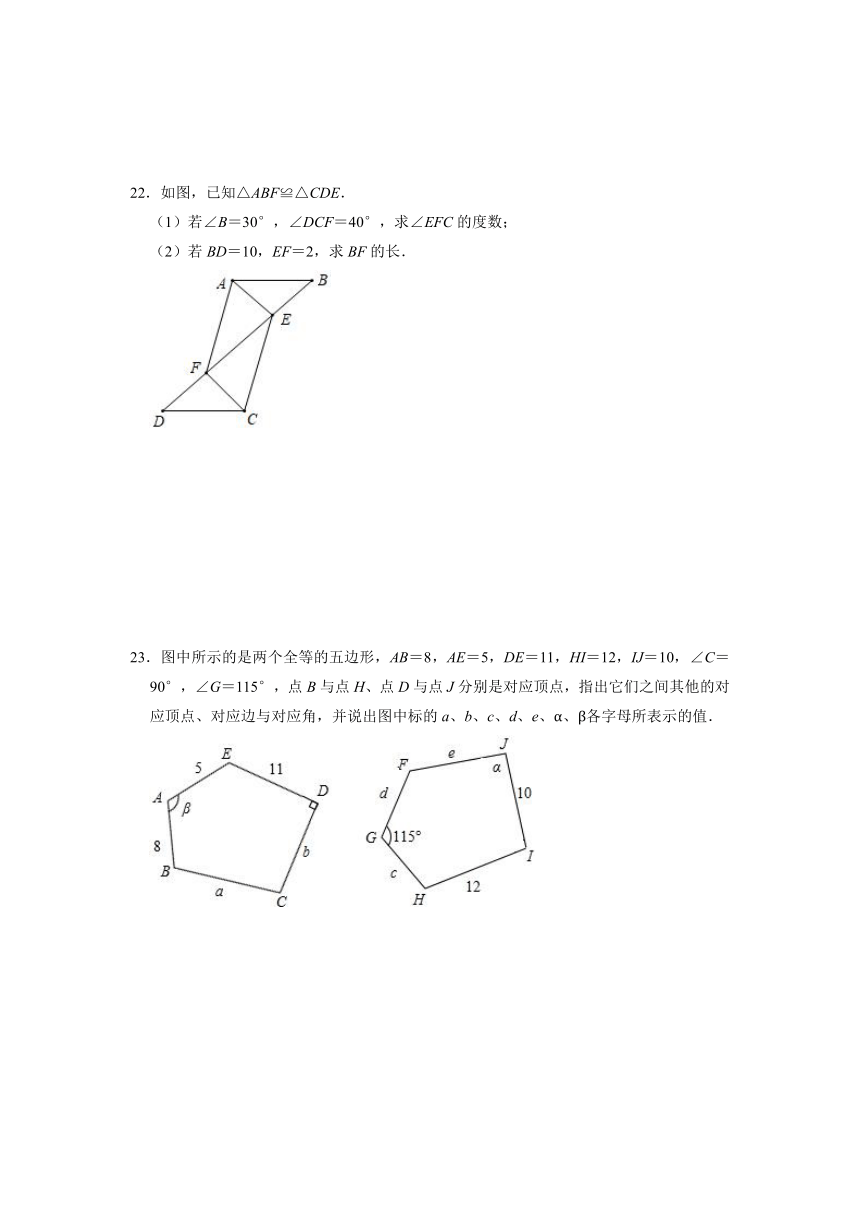
22.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
23.图中所示的是两个全等的五边形,AB=8,AE=5,DE=11,HI=12,IJ=10,∠C=90°,∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的a、b、c、d、e、α、β各字母所表示的值.
24.如图,△ABC≌△ADE,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
参考答案
1.解:观察发现:只有B选项的图形与已知图形全等,
故选:B.
2.解:A、不是全等形,故此选项错误;
B、不是全等形,故此选项错误;
C、是全等形,故此选项正确;
D、不是全等形,故此选项错误;
故选:C.
3.解:
在△ABC中,∠A=80°,∠B=40°,
∴∠C=180°﹣80°﹣40°=60°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=60°,
故选:C.
4.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB=70°,
∵∠ACB′=100°,
∴∠BCB′=∠ACB′﹣∠ACB=30°,
∴∠BCA′=∠A′CB′﹣∠BCB′=40°,
故选:C.
5.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
6.解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠EAC=∠BAD=70°﹣35°=35°,
故选:B.
7.解:∵△ABC≌△DEF,
∴∠B=∠DEF,∠F=∠ACB,
∴AB∥DE,AC∥DF,
无法得出BE=EC=CF
故选项D正确.
故选:D.
8.解:∵两个三角形全等,
∴边长为a的对角是对应角,
∴∠1=73°,
故选:C.
9.解:全等的两个图形的面积、周长均相等,但是周长、面积相等的两个图形不一定全等.
故选:C.
10.解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
11.解:∵△ABC≌△ADE,且点B与点D对应,点C与点E对应,
∴∠B=∠D,AC=AE,∠BAC=∠BAD,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠BAC=180°,∠BAC=28°,
∴∠ACE=∠AEC=(180°﹣∠BAC)=76°,∠BAD=28°,
∵∠D+∠CAD+∠ACE=180°,
∴∠D=180°﹣∠CAD﹣∠ACE=48°,
故答案为48.
12.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
13.解:∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∵∠BAD=40°,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36°.
14.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=45°.
故答案为:45°.
15.解:在△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5,
∵△ABC≌△EDB,
∴DE=AB=5.
故答案为:5.
16.解:∵两个三角形全等,
∴x=6,y=5,
∴x﹣y=6﹣5=1,
故答案为:1.
17.解:(1)与(6)是全等图形,
(2)与(5)(3)是全等图形,
故答案为:(6),(5)(3).
18.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
19.解:如图所示:
.
20.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
21.证明:∵△ABC≌△ADE,
∴∠C=∠AED,∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠CAE=∠BAD,
∵∠AEB=∠AED+∠DEB=∠CAE+∠C,
∴∠CAE=∠BED,
∴∠BED=∠BAD.
22.解:(1)∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°;
(2)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,即BE=DF,
∵BD=10,EF=2,
∴BE=(10﹣2)÷2=4,
∴BF=BE+EF=6.
23.解:对应顶点:A和G,E和F,C和I,
对应边:AB和GH,AE和GF,ED和FJ,CD和JI,BC和HI;
对应角:∠A和∠G,∠B和∠H,∠C和∠I,∠D和∠J,∠E和∠F;
∵两个五边形全等,
∴a=12,c=8,b=10,d=5,e=11,α=90°,β=115°.
24.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,
∴∠BAC=(120°﹣10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∴∠DFB=∠BAF+∠B=65°+25°=90°;
∵∠DFB=∠D+∠DGB,
∴∠DGB=90°﹣25°=65°
一、选择题
1.下列四个选项中的图形与下面的图形全等的是( )
A.B.C.D.
2.在下列每组图形中,是全等形的是( )
A.
B.
C.
D.
3.已知△ABC≌△A′B′C′,∠A=80°,∠B=40°,那么∠C′的度数为( )
A.80°
B.40°
C.60°
D.120°
4.如图△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30°
B.35°
C.40°
D.50°
5.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
6.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
7.如图所示,点B、E、C、F在一条直线上,△ABC≌△DEF,则下列结论正确的是( )
A.AB∥DE,但AC不平行于DF
B.BE=EC=CF
C.AC∥DF,但AB不平行于DE
D.AB∥DE,AC∥DF
8.图中的两个三角形全等,则∠1等于( )
A.45°
B.62°
C.73°
D.135°
9.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等
D.若两个图形周长相等,则它们一定是全等图形
10.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30
B.27
C.35
D.40
二、填空题
11.如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是
°.
12.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
13.如图,△ABC≌△ADE,且点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是
.
14.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
15.如图,在△ABC和△EDB中,∠C=∠EBD=90°,点E在AB上.若△ABC≌△EDB,AC=4,BC=3,则DE=
.
16.一个三角形的三边为3、5、x,另一个三角形的三边为y、3、6,若这两个三角形全等,则x﹣y=
.
17.如图,有6个条形方格图,在由实线围成的图形中,全等图形有:(1)与
;(2)与
.
18.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
三、解答题
19.如图,请沿图中的虚线,用三种方法将下列图形划分为两个全等图形.
20.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
21.如图,△ABC≌△ADE,点E在边BC上,求证:∠BED=∠BAD.
22.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
23.图中所示的是两个全等的五边形,AB=8,AE=5,DE=11,HI=12,IJ=10,∠C=90°,∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的a、b、c、d、e、α、β各字母所表示的值.
24.如图,△ABC≌△ADE,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
参考答案
1.解:观察发现:只有B选项的图形与已知图形全等,
故选:B.
2.解:A、不是全等形,故此选项错误;
B、不是全等形,故此选项错误;
C、是全等形,故此选项正确;
D、不是全等形,故此选项错误;
故选:C.
3.解:
在△ABC中,∠A=80°,∠B=40°,
∴∠C=180°﹣80°﹣40°=60°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=60°,
故选:C.
4.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB=70°,
∵∠ACB′=100°,
∴∠BCB′=∠ACB′﹣∠ACB=30°,
∴∠BCA′=∠A′CB′﹣∠BCB′=40°,
故选:C.
5.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
6.解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠EAC=∠BAD=70°﹣35°=35°,
故选:B.
7.解:∵△ABC≌△DEF,
∴∠B=∠DEF,∠F=∠ACB,
∴AB∥DE,AC∥DF,
无法得出BE=EC=CF
故选项D正确.
故选:D.
8.解:∵两个三角形全等,
∴边长为a的对角是对应角,
∴∠1=73°,
故选:C.
9.解:全等的两个图形的面积、周长均相等,但是周长、面积相等的两个图形不一定全等.
故选:C.
10.解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
11.解:∵△ABC≌△ADE,且点B与点D对应,点C与点E对应,
∴∠B=∠D,AC=AE,∠BAC=∠BAD,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠BAC=180°,∠BAC=28°,
∴∠ACE=∠AEC=(180°﹣∠BAC)=76°,∠BAD=28°,
∵∠D+∠CAD+∠ACE=180°,
∴∠D=180°﹣∠CAD﹣∠ACE=48°,
故答案为48.
12.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
13.解:∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∵∠BAD=40°,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36°.
14.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=45°.
故答案为:45°.
15.解:在△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5,
∵△ABC≌△EDB,
∴DE=AB=5.
故答案为:5.
16.解:∵两个三角形全等,
∴x=6,y=5,
∴x﹣y=6﹣5=1,
故答案为:1.
17.解:(1)与(6)是全等图形,
(2)与(5)(3)是全等图形,
故答案为:(6),(5)(3).
18.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
19.解:如图所示:
.
20.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
21.证明:∵△ABC≌△ADE,
∴∠C=∠AED,∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠CAE=∠BAD,
∵∠AEB=∠AED+∠DEB=∠CAE+∠C,
∴∠CAE=∠BED,
∴∠BED=∠BAD.
22.解:(1)∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°;
(2)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,即BE=DF,
∵BD=10,EF=2,
∴BE=(10﹣2)÷2=4,
∴BF=BE+EF=6.
23.解:对应顶点:A和G,E和F,C和I,
对应边:AB和GH,AE和GF,ED和FJ,CD和JI,BC和HI;
对应角:∠A和∠G,∠B和∠H,∠C和∠I,∠D和∠J,∠E和∠F;
∵两个五边形全等,
∴a=12,c=8,b=10,d=5,e=11,α=90°,β=115°.
24.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,
∴∠BAC=(120°﹣10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∴∠DFB=∠BAF+∠B=65°+25°=90°;
∵∠DFB=∠D+∠DGB,
∴∠DGB=90°﹣25°=65°
