22.3实际问题与二次函数(图形问题)课后练习 2021-2022学年人教版数学九年级上册(word版含解析)
文档属性
| 名称 | 22.3实际问题与二次函数(图形问题)课后练习 2021-2022学年人教版数学九年级上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 584.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 20:26:51 | ||
图片预览


文档简介
实际问题与二次函数(图形问题)
一、单选题
1.用一段长为20m的篱笆围成一个矩形菜园,设菜园的对角线长为xm,面积为ym2,则y与x的函数图象大致是( )
A.
B.
C.
D.
2.如果一个矩形的周长与面积的差是定值,我们称这个矩形为“定差值矩形”.如图,在矩形中,
,,,那么这个“定差值矩形”的对角线
的长的最小值为(
)
A.
B.
C.
D.
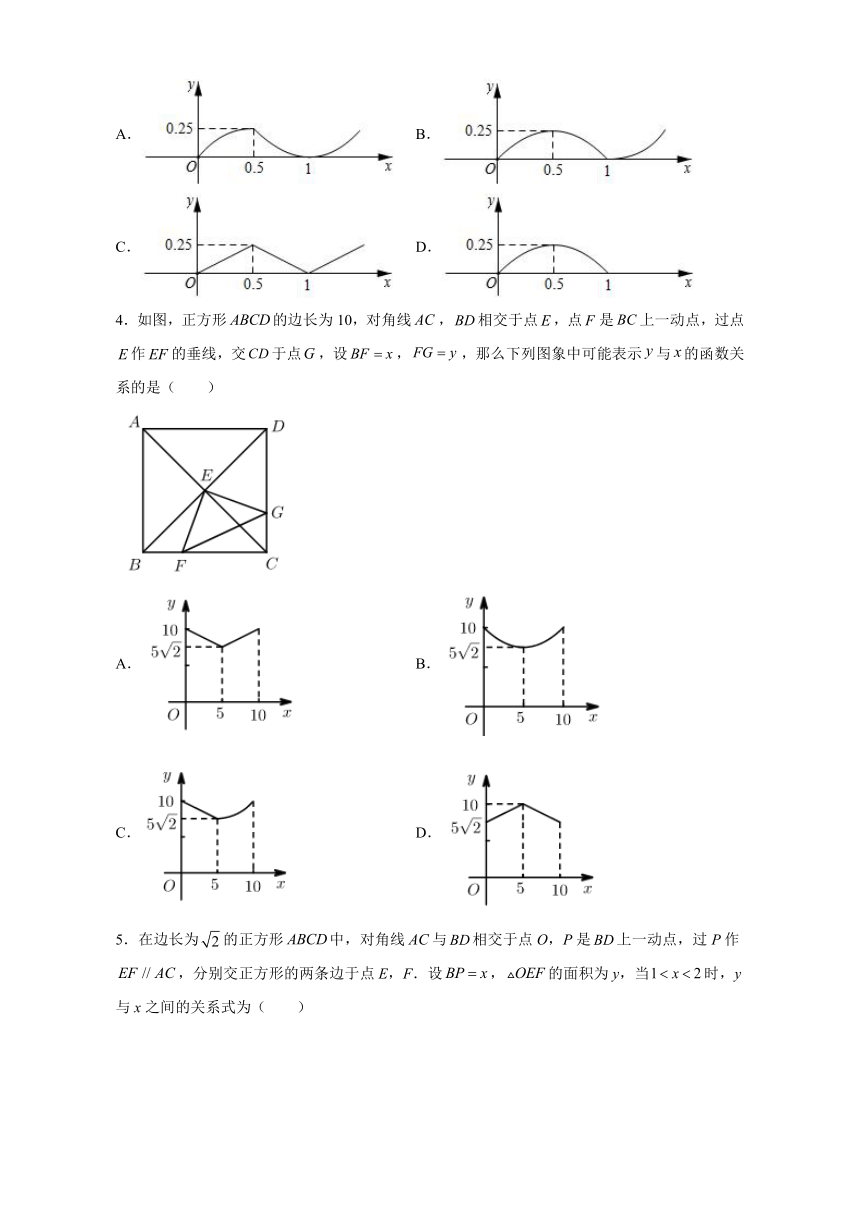
3.如图,四边形是边长为1的正方形,点E是射线上的动点(点E不与点A,点B重合),点F在线段的延长线上,且,连接,将绕点E顺时针旋转得到,连接.设,四边形的面积为y,下列图象能正确反映出y与x的函数关系的是(
)
A.
B.
C.
D.
4.如图,正方形的边长为10,对角线,相交于点,点是上一动点,过点作的垂线,交于点,设,,那么下列图象中可能表示与的函数关系的是(
)
A.
B.
C.
D.
5.在边长为的正方形中,对角线与相交于点O,P是上一动点,过P作,分别交正方形的两条边于点E,F.设,的面积为y,当时,y与x之间的关系式为(
)
A.
B.
C.
D.
6.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为(
)
A.9
B.10.5
C.12
D.15
7.已知二次函数的图象与轴交于A、B两点(点A在点B的左侧),顶点C,点C关于轴的对称点为D点,若四边形为正方形,则的值为(
)
A.
B.
C.
D.
8.如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1,将C1向右平移得到C2,C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为(
)
A.4
B.3
C.6
D.π
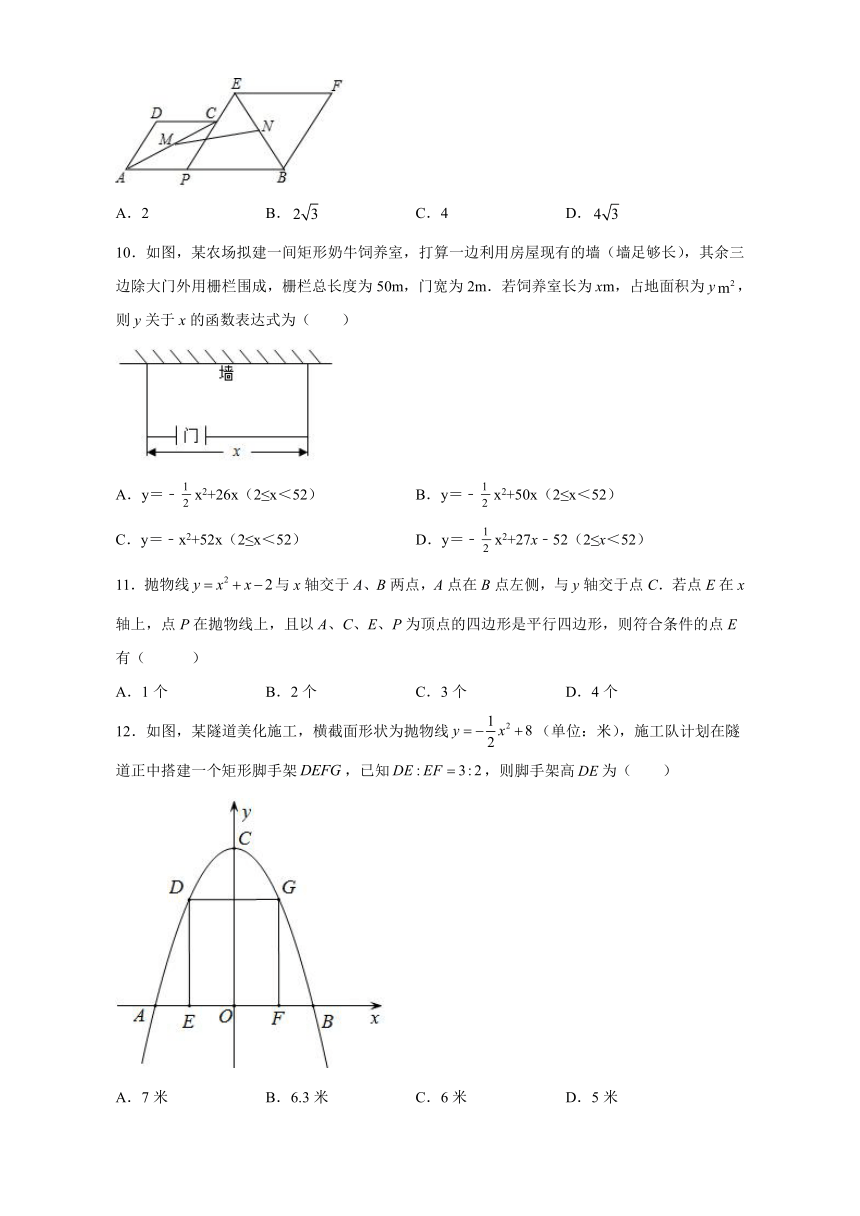
9.如图,已知,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,,M,N分别是对角线AC,BE的中点.当点Р在线段AB上移动时,点MN之间的距离最短为(
)
A.2
B.
C.4
D.
10.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y,则y关于x的函数表达式为( )
A.y=﹣x2+26x(2≤x<52)
B.y=﹣x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52)
D.y=﹣x2+27x﹣52(2≤x<52)
11.抛物线与x轴交于A、B两点,A点在B点左侧,与y轴交于点C.若点E在x轴上,点P在抛物线上,且以A、C、E、P为顶点的四边形是平行四边形,则符合条件的点E有( )
A.1个
B.2个
C.3个
D.4个
12.如图,某隧道美化施工,横截面形状为抛物线(单位:米),施工队计划在隧道正中搭建一个矩形脚手架,已知,则脚手架高为(
)
A.7米
B.6.3米
C.6米
D.5米
二、填空题
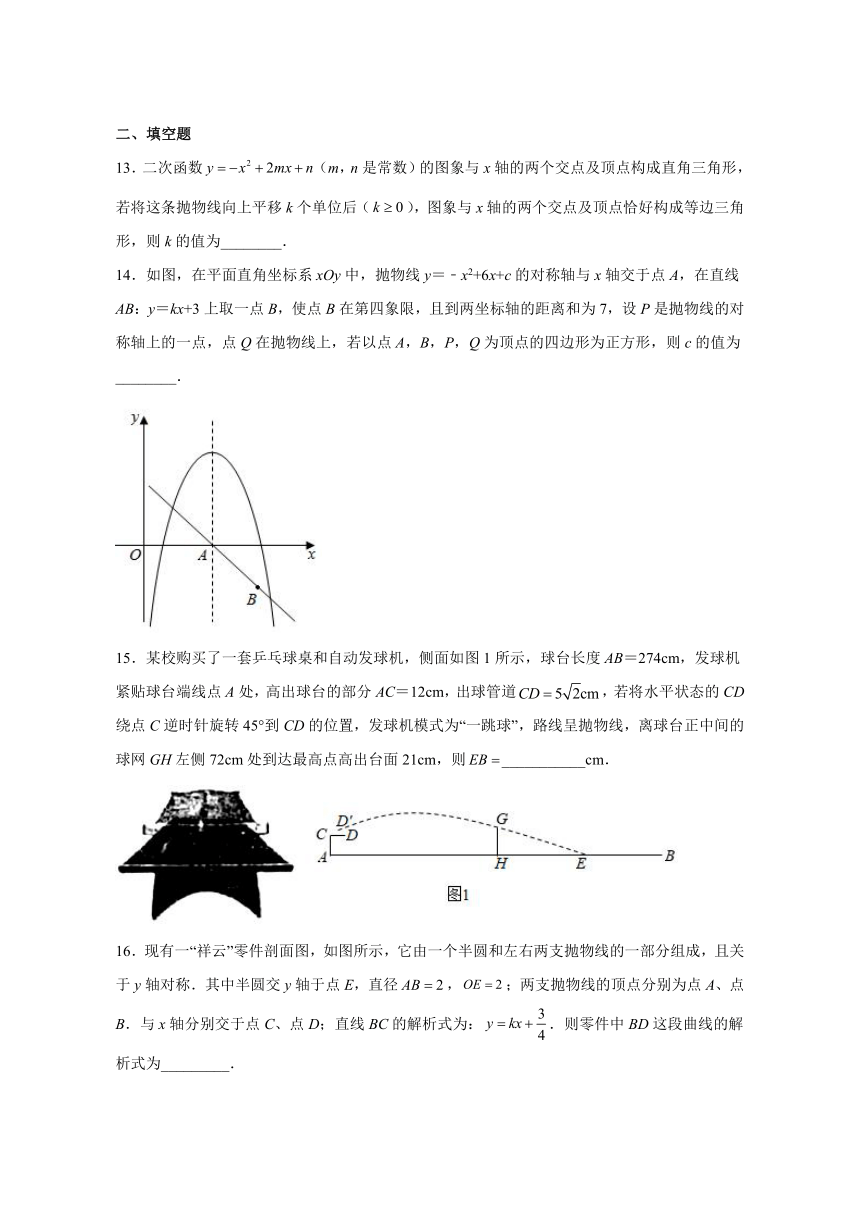
13.二次函数(m,n是常数)的图象与x轴的两个交点及顶点构成直角三角形,若将这条抛物线向上平移k个单位后(),图象与x轴的两个交点及顶点恰好构成等边三角形,则k的值为________.
14.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,在直线AB:y=kx+3上取一点B,使点B在第四象限,且到两坐标轴的距离和为7,设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A,B,P,Q为顶点的四边形为正方形,则c的值为________.
15.某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则___________cm.
16.现有一“祥云”零件剖面图,如图所示,它由一个半圆和左右两支抛物线的一部分组成,且关于y轴对称.其中半圆交y轴于点E,直径,;两支抛物线的顶点分别为点A、点B.与x轴分别交于点C、点D;直线BC的解析式为:.则零件中BD这段曲线的解析式为_________.
17.如图,中,,,等边三角形的顶点D,E,F分别在直角三角形的三边上,则长的最小值是____.
三、解答题
18.一个圆形喷水池的中央竖直安装了一个高为9米的柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,如果抛物线的最高点M离柱形喷水装置1米,离地面12米,若不计其他因素,水池的半径OB至少为多少米时,才能使喷出的水流不落在池外?
19.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
20.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长为.设垂直于墙的一边长为.
(1)当为何值时,菜园的面积为;
(2)当为何值时,菜园的面积最大?最大面积是多少?
21.用规格长为6m,宽为0.1m的铝合金型材,恰好制作成一个“日”字型窗子的边框(如图1,不计耗损),中间装长xm,宽ym完全一样的两张玻璃.这个窗子要装入最大边长为1.5m的正方形墙洞(如图2)中.
(1)求y与x之间的函数关系式,并求出x的取值范围.
(2)这个窗子的采光面积(两张玻璃面积之和)存在最大值吗?如果有,请求出来;如果没有,请说明理由.
22.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体处,另一端固定在离地面高2米的墙体处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度(米)与其离墙体的水平距离(米)之间的关系满足,现测得,两墙体之间的水平距离为6米.
图2
(1)直接写出,的值;
(2)求大棚的最高处到地面的距离;
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
参考答案
1.B
解:设矩形的长为am,宽为bm,
根据题意,得a+b=20÷2=10(m),
∵菜园的对角线长为xm,
∴a2+b2=x2,
∵x,,
∴x2=a2+b2≥,仅当取等号,
∴x2≥2×5×5,
∴x≥,
,
∵(a+b)2=a2+2ab+b2,
∴102=x2+2ab,
∴,
∴0≤y<25,且x=时,y=25,
∴y与x函数图象是二次函数的图象,即开口方向向下的抛物线.
故选:B.
2.C
解:∵在矩形中,,,,
∴,
∴,
∵,
∴,
∴,
∴当时,,
∴有最小值为(取正值),
故选:C.
3.B
解:∵四边形ABCD是边长为1的正方形,
∴∠DAB=90°,AD=AB,
在△ADE和△ABF中,
∴△ADE≌△ABF(SAS),
∴∠ADE=∠ABF,DE=BF,
∵∠DEG=90°,
∴∠ADE+∠AED=∠AED+∠BEG,
∴∠BEG=∠ADE,
∴∠BEG=∠ABF,
∴EGBF,
∵DE=BF,DE=GE,
∴EG=BF,
∴四边形BFEG是平行四边形,
∴四边形EFBG的面积=2△BEF的面积=2BE?AF,
设AE=x,四边形EFBG的面积为y,
当0≤x≤1时,y=(1-x)?x=-x2+x;
当x>1时,y=(x-1)?x=x2-x;
综上可知,当0≤x≤1时,函数图象是开口向下的抛物线;当x>1时,函数图象是开口向上的抛物线,
符合上述特征的只有B,
故选:B.
4.B
解:∵四边形ABCD是正方形,
∴∠EBF=∠ECG=45°,AC⊥BD,EB=EC,
∵EF⊥EG,
∴∠BEC=∠FEG=90°,
∴∠BEF=∠CEG,
∴△BEF≌△CEG(ASA),
∴BF=CG,
在Rt△CFG中,∵FG2=CF2+CG2,
即y2=x2+(10-x)2=2(x-5)2+50,
∴可以表示y与x的函数关系的是选项B.
故选:B.
5.C
解:∵四边形ABCD是正方形,
∴AC=BD=2,OB=OD=BD=1,
∵当1<x<2时,即P在OD上,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2=(2-x):1,
∴EF=4-2x,
∴y=EF?OP=×(4?2x)?(x?1)=-x2+3x-2.
故选:C.
6.A
解:设AE=CF=x,
∵四边形AEMH和四边形CFNG是正方形,
∴BE=DG=5-x,BF=DH=7-x,NP=MQ=2x-5,NQ=2x-7,
则阴影部分的面积S=
=
∵0<x≤5,
∴当x=4时,S最小,且为9.
7.C
解:二次函数的图象与轴交于A、B两点,
,,
抛物线的对称轴为直线,
设顶点C的坐标为,
四边形为正方形,
,
或,
把C点的坐标代入得:或,
解得:,
故选:C.
8.A
解:令y=0,则:x=±1,令x=0,则y=2,则:OB=1,BD=2,OE=2,
S阴影部分图形=S四边形BDFE=BD×OE=2×2=4.
故选:A.
9.B
解:连接PM、PN.
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠CPM=∠APC=60°,∠EPN=∠EPB=30°,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),
∴MN=,
∴a=3时,MN有最小值,最小值为2,
故选:B.
10.A
解:y关于x的函数表达式为:y(50+2﹣x)x
x2+26x(2≤x<52).
故选:A.
11.D
解:由图象可知,满足条件的A、C、E、P为顶点的四边形是平行四边形有四个,
故选:D.
12.C
解:∵,矩形脚手架在隧道正中,
∴设,,则,
∴D点坐标为,
将代入
得,
解得或(舍)
∴
故选:C.
13.2
解:∵,
∴抛物线的顶点坐标为,
抛物线与x轴的两交点的连线段的长度.
当抛物线与轴的两个交点及顶点构成直角三角形时,由抛物线的对称性可知该直角三角形为等腰直角三角形,
∴,
则,
若将这条抛物线向上平移k个单位后,图象与轴的两个交点及顶点恰好构成等边三角形,
此时顶点的纵坐标为.
所以,
则,
所以.
故k的值为2.
14.﹣5或﹣7
解:∵抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,
且对称轴为直线x=﹣=3,
∴A(3,0),
∵点A在直线AB:y=kx+3上,
∴0=3k+3,
解得k=﹣1,
∴直线AB为y=﹣x+3,
∴设点B的坐标为(x,﹣x+3)
∵点B在第四象限,且到两坐标轴的距离和为7,
∴x﹣3+x=7,
解得x=5,
∴B(5,﹣2),
∴B到对称轴的距离为5﹣3=2,B到x轴的距离为2,
当AB是正方形对角线时,P(3,﹣2),则Q(5,0),
当AB是正方形的边时,P(3,﹣4),则Q(1,﹣2)
∵点Q在抛物线上,
∴把Q(5,0)代入y=﹣x2+6x+c得:
0=﹣25+30+c,
解得c=﹣5;
把Q(1,﹣2)代入y=﹣x2+6x+c得:
﹣2=﹣1+6+c,
解得c=﹣7,
∴,c的值为﹣5或﹣7,
故答案为:﹣5或﹣7.
15.
解:以AC为y轴,以AB为x轴,A为原点建立平面直角坐标系,如图,
设抛物线最高点为N,对称轴MN与x轴交于M,则MN=21,
∴AB=274,
∵GH是AB正中间,
∴AH=AB=137,
∴AM=AH-MH=13772=65,
设抛物线为:y=a(x-65)2+21(a<0),
过D′作D′P⊥x轴交CD于点Q,交x轴于点P,
则∠CQD′=∠APQ=90°,
∵旋转45°,
∴CD′=,
CQ=D′Q=CD′cos∠D′CD=5,
∴D′P=D′Q+PQ=5+12=17,
∴D′(5,17)代入抛物线得:
a×(5-65)2+21=17,
∴,
∴y=(x65)2+21,
令y=0,则(x65)2+21=0,
解得:x1=65+30,x2=65-30(舍去),
∴E(65+30,0),
∴EB=AB-AE=274-(65+30)=(209-30)(cm),
故答案为:20930.
16.
解:记AB与y轴的交点为F,
∵AB=2,且半圆关于y轴对称,
∴FA=FB=FE=1,
∵OE=2,
∴,
则右侧抛物线的顶点B坐标为,
将点代入得,
解得,
∴,
当时,,
解得,
∴,
则,
设右侧抛物线解析式为,
将点代入解析式得,
解得,
∴.
故答案为:.
17.
解:过点D作于点G,
∵,是等边三角形
∴,
∴,
∵DE=DF,
∴,
∴.
设,
则,
在中,,
∴.
∴当时,最小,.
故答案是:.
18.3米
解:由题意可得:抛物线顶点坐标为(1,12),A点坐标为(0,9),
故设抛物线解析式为:,
则,
解得:a=﹣3,
故抛物线解析式为:,
当y=0时,
解得:x1=﹣1,x2=3,
则水池的半径OB至少为3米时,才能使喷出的水流不落在池外.
19.(1)y=2x2﹣42x+160;(2)竖甬道的宽度为1米.
解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
20.(1)10;
(2)当
时,菜园的面积最大,最大面积是
.
解:(1)设垂直于墙的一边长为,则平行于墙的边长为
,
根据题意得:
,
解得:
,
,
∵
,即
,
∴,不符合题意,舍去,
∴当时,菜园的面积为;
(2)设菜园的面积为
,根据题意得:
,
∵
,
∴当
时,
的值最大,即菜园的面积最大,最大面积是
.
21.(1)y=﹣0.75x+1.35,1≤x≤1.3;(2)这个窗子的采光面积有最大值,最大值为1.2m2,见解析.
解:(1)由题意,得3x+2(2y+0.1×3)=6,
整理,得3x+4y=5.4,
∴y=﹣0.75x+1.35,
∴y与x之间的函数关系式为y=﹣0.75x+1.35,
由题意,得,
解得1≤x≤1.3,
即x的取值范围是1≤x≤1.3;
(2)设这个窗子的采光面积为Sm2,
由题意,得S=2xy=2x(﹣0.75x+1.35)=﹣1.5x2+2.7x,
配方,得S=﹣1.5(x﹣0.9)2+1.215,
∵a=﹣1.5<0,对称轴为x=0.9,
∴当x>0.9时,y随x的增大而减小,
∵1≤x≤1.3,
∴当x=1时,S有最大值,
S最大=1.2,
答:这个窗子的采光面积有最大值,最大值为1.2m2.
22.(1),;(2)米;(3)352
解:(1)由题意知点A坐标为,点B坐标为,
将A、B坐标代入得:
解得:,
故,;
(2)由,
可得当时,有最大值,
即大棚最高处到地面的距离为米;
(3)由,解得,,
又因为,
可知大棚内可以搭建支架的土地的宽为(米),
又大棚的长为16米,故需要搭建支架部分的土地面积为(平方米)
共需要(根)竹竿.
一、单选题
1.用一段长为20m的篱笆围成一个矩形菜园,设菜园的对角线长为xm,面积为ym2,则y与x的函数图象大致是( )
A.
B.
C.
D.
2.如果一个矩形的周长与面积的差是定值,我们称这个矩形为“定差值矩形”.如图,在矩形中,
,,,那么这个“定差值矩形”的对角线
的长的最小值为(
)
A.
B.
C.
D.
3.如图,四边形是边长为1的正方形,点E是射线上的动点(点E不与点A,点B重合),点F在线段的延长线上,且,连接,将绕点E顺时针旋转得到,连接.设,四边形的面积为y,下列图象能正确反映出y与x的函数关系的是(
)
A.
B.
C.
D.
4.如图,正方形的边长为10,对角线,相交于点,点是上一动点,过点作的垂线,交于点,设,,那么下列图象中可能表示与的函数关系的是(
)
A.
B.
C.
D.
5.在边长为的正方形中,对角线与相交于点O,P是上一动点,过P作,分别交正方形的两条边于点E,F.设,的面积为y,当时,y与x之间的关系式为(
)
A.
B.
C.
D.
6.如图,在矩形中,,点E,F分别是,上的点,且满足.分别以,为边向矩形内部构造正方形和正方形,记阴影部分的面积为S,则S的最小值为(
)
A.9
B.10.5
C.12
D.15
7.已知二次函数的图象与轴交于A、B两点(点A在点B的左侧),顶点C,点C关于轴的对称点为D点,若四边形为正方形,则的值为(
)
A.
B.
C.
D.
8.如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1,将C1向右平移得到C2,C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为(
)
A.4
B.3
C.6
D.π
9.如图,已知,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,,M,N分别是对角线AC,BE的中点.当点Р在线段AB上移动时,点MN之间的距离最短为(
)
A.2
B.
C.4
D.
10.如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y,则y关于x的函数表达式为( )
A.y=﹣x2+26x(2≤x<52)
B.y=﹣x2+50x(2≤x<52)
C.y=﹣x2+52x(2≤x<52)
D.y=﹣x2+27x﹣52(2≤x<52)
11.抛物线与x轴交于A、B两点,A点在B点左侧,与y轴交于点C.若点E在x轴上,点P在抛物线上,且以A、C、E、P为顶点的四边形是平行四边形,则符合条件的点E有( )
A.1个
B.2个
C.3个
D.4个
12.如图,某隧道美化施工,横截面形状为抛物线(单位:米),施工队计划在隧道正中搭建一个矩形脚手架,已知,则脚手架高为(
)
A.7米
B.6.3米
C.6米
D.5米
二、填空题
13.二次函数(m,n是常数)的图象与x轴的两个交点及顶点构成直角三角形,若将这条抛物线向上平移k个单位后(),图象与x轴的两个交点及顶点恰好构成等边三角形,则k的值为________.
14.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,在直线AB:y=kx+3上取一点B,使点B在第四象限,且到两坐标轴的距离和为7,设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A,B,P,Q为顶点的四边形为正方形,则c的值为________.
15.某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球”,路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则___________cm.
16.现有一“祥云”零件剖面图,如图所示,它由一个半圆和左右两支抛物线的一部分组成,且关于y轴对称.其中半圆交y轴于点E,直径,;两支抛物线的顶点分别为点A、点B.与x轴分别交于点C、点D;直线BC的解析式为:.则零件中BD这段曲线的解析式为_________.
17.如图,中,,,等边三角形的顶点D,E,F分别在直角三角形的三边上,则长的最小值是____.
三、解答题
18.一个圆形喷水池的中央竖直安装了一个高为9米的柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,如果抛物线的最高点M离柱形喷水装置1米,离地面12米,若不计其他因素,水池的半径OB至少为多少米时,才能使喷出的水流不落在池外?
19.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
20.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长为.设垂直于墙的一边长为.
(1)当为何值时,菜园的面积为;
(2)当为何值时,菜园的面积最大?最大面积是多少?
21.用规格长为6m,宽为0.1m的铝合金型材,恰好制作成一个“日”字型窗子的边框(如图1,不计耗损),中间装长xm,宽ym完全一样的两张玻璃.这个窗子要装入最大边长为1.5m的正方形墙洞(如图2)中.
(1)求y与x之间的函数关系式,并求出x的取值范围.
(2)这个窗子的采光面积(两张玻璃面积之和)存在最大值吗?如果有,请求出来;如果没有,请说明理由.
22.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体处,另一端固定在离地面高2米的墙体处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度(米)与其离墙体的水平距离(米)之间的关系满足,现测得,两墙体之间的水平距离为6米.
图2
(1)直接写出,的值;
(2)求大棚的最高处到地面的距离;
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
参考答案
1.B
解:设矩形的长为am,宽为bm,
根据题意,得a+b=20÷2=10(m),
∵菜园的对角线长为xm,
∴a2+b2=x2,
∵x,,
∴x2=a2+b2≥,仅当取等号,
∴x2≥2×5×5,
∴x≥,
,
∵(a+b)2=a2+2ab+b2,
∴102=x2+2ab,
∴,
∴0≤y<25,且x=时,y=25,
∴y与x函数图象是二次函数的图象,即开口方向向下的抛物线.
故选:B.
2.C
解:∵在矩形中,,,,
∴,
∴,
∵,
∴,
∴,
∴当时,,
∴有最小值为(取正值),
故选:C.
3.B
解:∵四边形ABCD是边长为1的正方形,
∴∠DAB=90°,AD=AB,
在△ADE和△ABF中,
∴△ADE≌△ABF(SAS),
∴∠ADE=∠ABF,DE=BF,
∵∠DEG=90°,
∴∠ADE+∠AED=∠AED+∠BEG,
∴∠BEG=∠ADE,
∴∠BEG=∠ABF,
∴EGBF,
∵DE=BF,DE=GE,
∴EG=BF,
∴四边形BFEG是平行四边形,
∴四边形EFBG的面积=2△BEF的面积=2BE?AF,
设AE=x,四边形EFBG的面积为y,
当0≤x≤1时,y=(1-x)?x=-x2+x;
当x>1时,y=(x-1)?x=x2-x;
综上可知,当0≤x≤1时,函数图象是开口向下的抛物线;当x>1时,函数图象是开口向上的抛物线,
符合上述特征的只有B,
故选:B.
4.B
解:∵四边形ABCD是正方形,
∴∠EBF=∠ECG=45°,AC⊥BD,EB=EC,
∵EF⊥EG,
∴∠BEC=∠FEG=90°,
∴∠BEF=∠CEG,
∴△BEF≌△CEG(ASA),
∴BF=CG,
在Rt△CFG中,∵FG2=CF2+CG2,
即y2=x2+(10-x)2=2(x-5)2+50,
∴可以表示y与x的函数关系的是选项B.
故选:B.
5.C
解:∵四边形ABCD是正方形,
∴AC=BD=2,OB=OD=BD=1,
∵当1<x<2时,即P在OD上,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2=(2-x):1,
∴EF=4-2x,
∴y=EF?OP=×(4?2x)?(x?1)=-x2+3x-2.
故选:C.
6.A
解:设AE=CF=x,
∵四边形AEMH和四边形CFNG是正方形,
∴BE=DG=5-x,BF=DH=7-x,NP=MQ=2x-5,NQ=2x-7,
则阴影部分的面积S=
=
∵0<x≤5,
∴当x=4时,S最小,且为9.
7.C
解:二次函数的图象与轴交于A、B两点,
,,
抛物线的对称轴为直线,
设顶点C的坐标为,
四边形为正方形,
,
或,
把C点的坐标代入得:或,
解得:,
故选:C.
8.A
解:令y=0,则:x=±1,令x=0,则y=2,则:OB=1,BD=2,OE=2,
S阴影部分图形=S四边形BDFE=BD×OE=2×2=4.
故选:A.
9.B
解:连接PM、PN.
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠CPM=∠APC=60°,∠EPN=∠EPB=30°,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),
∴MN=,
∴a=3时,MN有最小值,最小值为2,
故选:B.
10.A
解:y关于x的函数表达式为:y(50+2﹣x)x
x2+26x(2≤x<52).
故选:A.
11.D
解:由图象可知,满足条件的A、C、E、P为顶点的四边形是平行四边形有四个,
故选:D.
12.C
解:∵,矩形脚手架在隧道正中,
∴设,,则,
∴D点坐标为,
将代入
得,
解得或(舍)
∴
故选:C.
13.2
解:∵,
∴抛物线的顶点坐标为,
抛物线与x轴的两交点的连线段的长度.
当抛物线与轴的两个交点及顶点构成直角三角形时,由抛物线的对称性可知该直角三角形为等腰直角三角形,
∴,
则,
若将这条抛物线向上平移k个单位后,图象与轴的两个交点及顶点恰好构成等边三角形,
此时顶点的纵坐标为.
所以,
则,
所以.
故k的值为2.
14.﹣5或﹣7
解:∵抛物线y=﹣x2+6x+c的对称轴与x轴交于点A,
且对称轴为直线x=﹣=3,
∴A(3,0),
∵点A在直线AB:y=kx+3上,
∴0=3k+3,
解得k=﹣1,
∴直线AB为y=﹣x+3,
∴设点B的坐标为(x,﹣x+3)
∵点B在第四象限,且到两坐标轴的距离和为7,
∴x﹣3+x=7,
解得x=5,
∴B(5,﹣2),
∴B到对称轴的距离为5﹣3=2,B到x轴的距离为2,
当AB是正方形对角线时,P(3,﹣2),则Q(5,0),
当AB是正方形的边时,P(3,﹣4),则Q(1,﹣2)
∵点Q在抛物线上,
∴把Q(5,0)代入y=﹣x2+6x+c得:
0=﹣25+30+c,
解得c=﹣5;
把Q(1,﹣2)代入y=﹣x2+6x+c得:
﹣2=﹣1+6+c,
解得c=﹣7,
∴,c的值为﹣5或﹣7,
故答案为:﹣5或﹣7.
15.
解:以AC为y轴,以AB为x轴,A为原点建立平面直角坐标系,如图,
设抛物线最高点为N,对称轴MN与x轴交于M,则MN=21,
∴AB=274,
∵GH是AB正中间,
∴AH=AB=137,
∴AM=AH-MH=13772=65,
设抛物线为:y=a(x-65)2+21(a<0),
过D′作D′P⊥x轴交CD于点Q,交x轴于点P,
则∠CQD′=∠APQ=90°,
∵旋转45°,
∴CD′=,
CQ=D′Q=CD′cos∠D′CD=5,
∴D′P=D′Q+PQ=5+12=17,
∴D′(5,17)代入抛物线得:
a×(5-65)2+21=17,
∴,
∴y=(x65)2+21,
令y=0,则(x65)2+21=0,
解得:x1=65+30,x2=65-30(舍去),
∴E(65+30,0),
∴EB=AB-AE=274-(65+30)=(209-30)(cm),
故答案为:20930.
16.
解:记AB与y轴的交点为F,
∵AB=2,且半圆关于y轴对称,
∴FA=FB=FE=1,
∵OE=2,
∴,
则右侧抛物线的顶点B坐标为,
将点代入得,
解得,
∴,
当时,,
解得,
∴,
则,
设右侧抛物线解析式为,
将点代入解析式得,
解得,
∴.
故答案为:.
17.
解:过点D作于点G,
∵,是等边三角形
∴,
∴,
∵DE=DF,
∴,
∴.
设,
则,
在中,,
∴.
∴当时,最小,.
故答案是:.
18.3米
解:由题意可得:抛物线顶点坐标为(1,12),A点坐标为(0,9),
故设抛物线解析式为:,
则,
解得:a=﹣3,
故抛物线解析式为:,
当y=0时,
解得:x1=﹣1,x2=3,
则水池的半径OB至少为3米时,才能使喷出的水流不落在池外.
19.(1)y=2x2﹣42x+160;(2)竖甬道的宽度为1米.
解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
20.(1)10;
(2)当
时,菜园的面积最大,最大面积是
.
解:(1)设垂直于墙的一边长为,则平行于墙的边长为
,
根据题意得:
,
解得:
,
,
∵
,即
,
∴,不符合题意,舍去,
∴当时,菜园的面积为;
(2)设菜园的面积为
,根据题意得:
,
∵
,
∴当
时,
的值最大,即菜园的面积最大,最大面积是
.
21.(1)y=﹣0.75x+1.35,1≤x≤1.3;(2)这个窗子的采光面积有最大值,最大值为1.2m2,见解析.
解:(1)由题意,得3x+2(2y+0.1×3)=6,
整理,得3x+4y=5.4,
∴y=﹣0.75x+1.35,
∴y与x之间的函数关系式为y=﹣0.75x+1.35,
由题意,得,
解得1≤x≤1.3,
即x的取值范围是1≤x≤1.3;
(2)设这个窗子的采光面积为Sm2,
由题意,得S=2xy=2x(﹣0.75x+1.35)=﹣1.5x2+2.7x,
配方,得S=﹣1.5(x﹣0.9)2+1.215,
∵a=﹣1.5<0,对称轴为x=0.9,
∴当x>0.9时,y随x的增大而减小,
∵1≤x≤1.3,
∴当x=1时,S有最大值,
S最大=1.2,
答:这个窗子的采光面积有最大值,最大值为1.2m2.
22.(1),;(2)米;(3)352
解:(1)由题意知点A坐标为,点B坐标为,
将A、B坐标代入得:
解得:,
故,;
(2)由,
可得当时,有最大值,
即大棚最高处到地面的距离为米;
(3)由,解得,,
又因为,
可知大棚内可以搭建支架的土地的宽为(米),
又大棚的长为16米,故需要搭建支架部分的土地面积为(平方米)
共需要(根)竹竿.
同课章节目录
