12.2三角形全等的判定能力提升训练2021-2022学年八年级数学人教版上册(word版含解析)
文档属性
| 名称 | 12.2三角形全等的判定能力提升训练2021-2022学年八年级数学人教版上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 20:34:39 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学上册《12.2三角形全等的判定》能力提升训练(附答案)
一、选择题
1.如图,在△ABC中,∠C=90°,点D为BC上一点,DE⊥AB于E,并且DE=DC,F为AC上一点,则下列结论中正确的是( )
A.DE=DF
B.BD=FD
C.∠1=∠2
D.AB=AC
2.一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
3.如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是( )
A.ASA
B.SSS
C.AAS
D.SAS
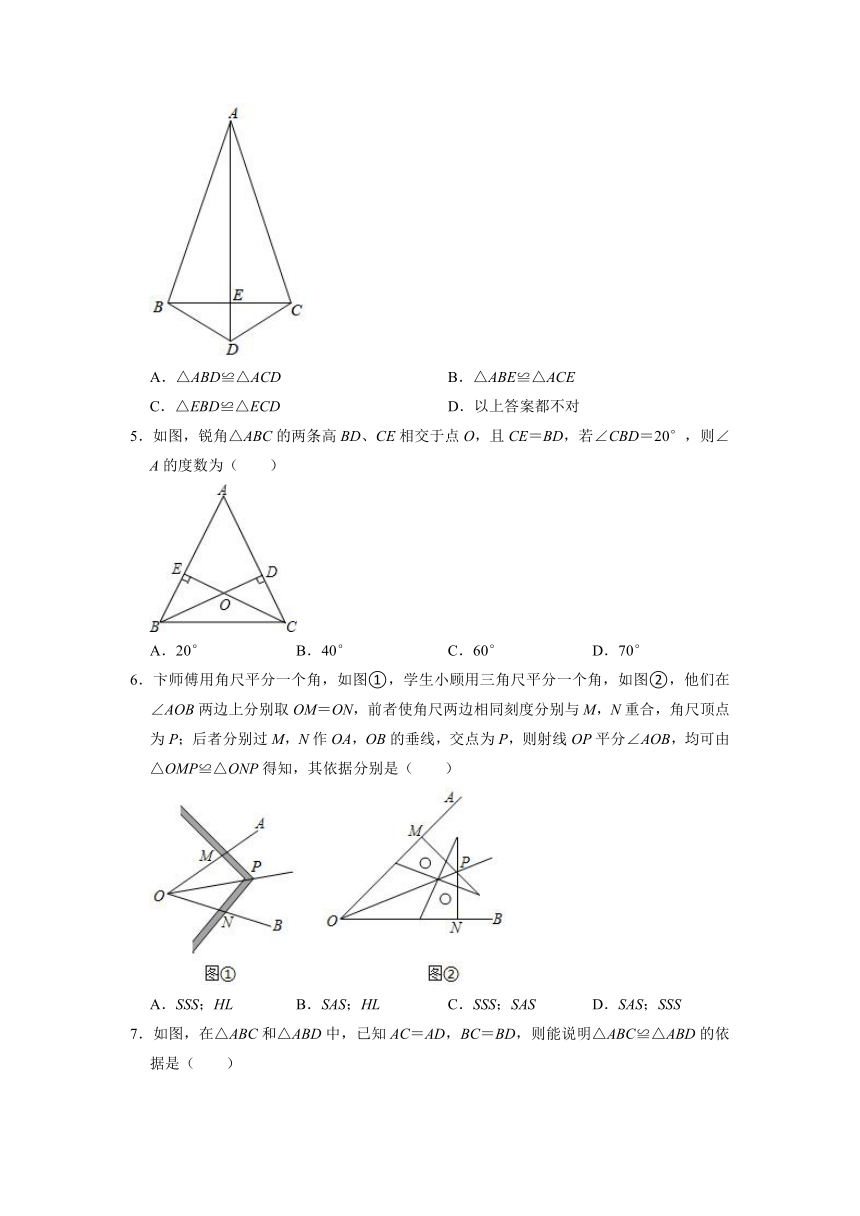
4.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△EBD≌△ECD
D.以上答案都不对
5.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20°
B.40°
C.60°
D.70°
6.卞师傅用角尺平分一个角,如图①,学生小顾用三角尺平分一个角,如图②,他们在∠AOB两边上分别取OM=ON,前者使角尺两边相同刻度分别与M,N重合,角尺顶点为P;后者分别过M,N作OA,OB的垂线,交点为P,则射线OP平分∠AOB,均可由△OMP≌△ONP得知,其依据分别是( )
A.SSS;HL
B.SAS;HL
C.SSS;SAS
D.SAS;SSS
7.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是( )
A.SAS
B.ASA
C.SSS
D.HL
8.使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.斜边及一条直角边对应相等
9.如图,点A,D,C,F在同一条直线上,AD=CF,∠F=∠ACB,再补充下列一个条件,不能证明△ABC≌△DEF的是( )
A.BC=EF
B.AB∥DE
C.∠B=∠E
D.AB=DE
10.如图,若∠1=∠2,则( )
A.AD∥BC
B.AD=BC
C.CD∥AB
D.AB=CD
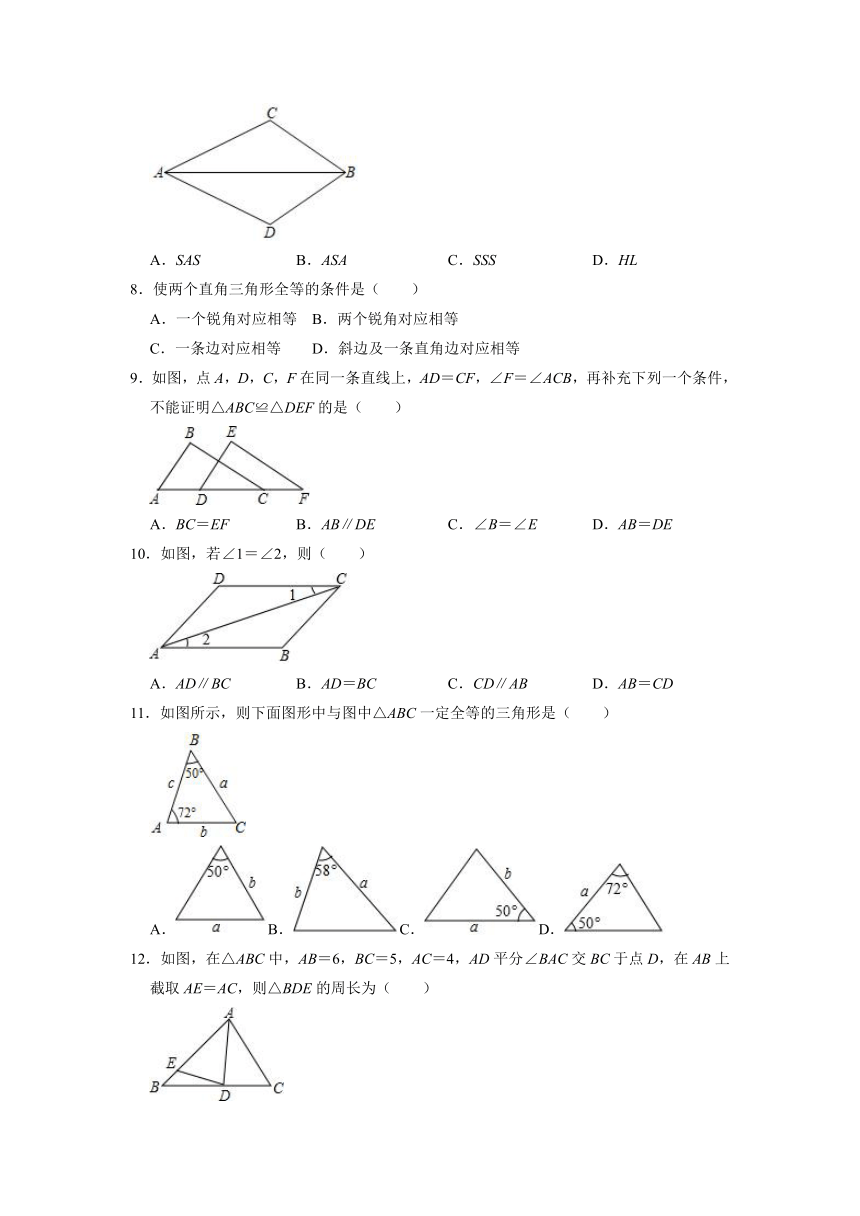
11.如图所示,则下面图形中与图中△ABC一定全等的三角形是( )
A.B.C.D.
12.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8
B.7
C.6
D.5
13.如图,已知∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于点D,AD=2.5cm,DE=1.7cm,则BE=( )
A.1cm
B.0.8cm
C.4.2cm
D.1.5cm
二、填空题
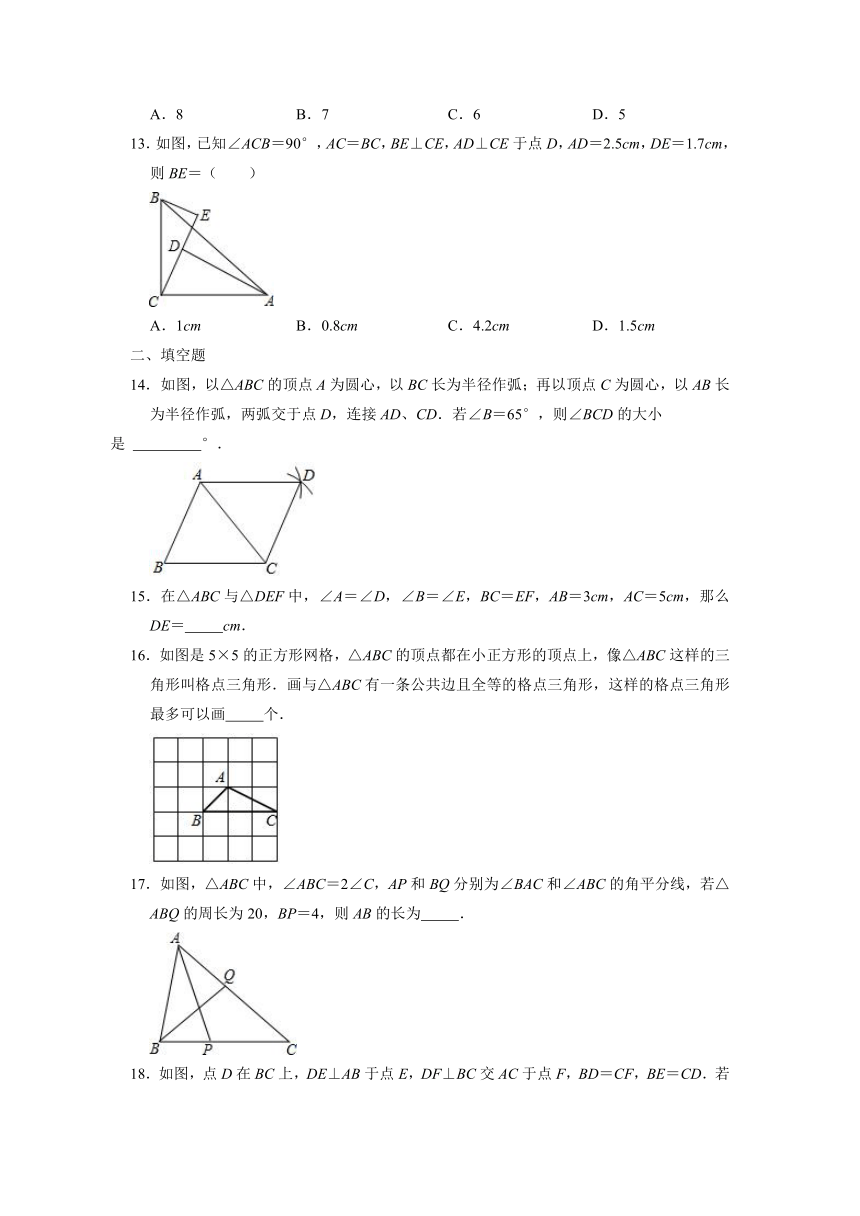
如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD、CD.若∠B=65°,则∠BCD的大小
是
°.
15.在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE=
cm.
16.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画
个.
17.如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为
.
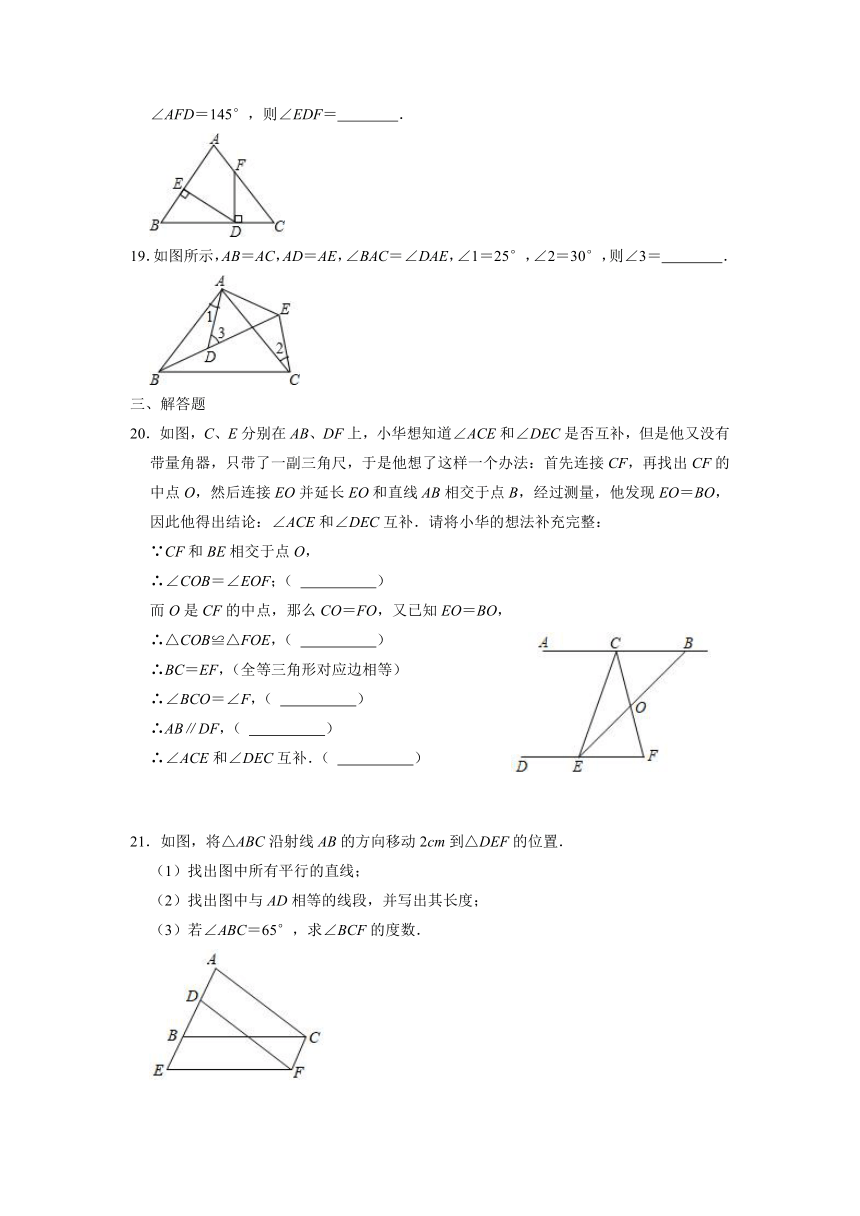
18.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=
.
19.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
三、解答题
20.如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他又没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补.请将小华的想法补充完整:
∵CF和BE相交于点O,
∴∠COB=∠EOF;(
)
而O是CF的中点,那么CO=FO,又已知EO=BO,
∴△COB≌△FOE,(
)
∴BC=EF,(全等三角形对应边相等)
∴∠BCO=∠F,(
)
∴AB∥DF,(
)
∴∠ACE和∠DEC互补.(
)
21.如图,将△ABC沿射线AB的方向移动2cm到△DEF的位置.
(1)找出图中所有平行的直线;
(2)找出图中与AD相等的线段,并写出其长度;
(3)若∠ABC=65°,求∠BCF的度数.
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BO平分∠DBC,交CD于点O,E为AB上一点,连接OE,且OE∥AC.
(1)∠A与∠BCD相等吗?请说明理由;
(2)△BOE与△BOC是否全等?为什么?
(3)若BC=5,AC=12,BD=,求出△ACE的面积.
23.已知,在△ABC中,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,且AD=CE.
(1)求证:∠ACB=90°;
(2)点O为AB的中点,连接OD,OE.请判断△ODE的形状?并说明理由.
参考答案
1.解:(1)在直角三角形DCF中,利用斜边长度大于直角边长度,可以得到DF>DC,又DC=DE,所以DF>DE,
故A选项错误;
(2)△BDE与△DCF,只满足∠DEB=∠DCF=90°,DC=DE的条件,不能判定两个三角形全等,故不能得到BD=FD,
另一方面,假设BD=FD,
在Rt△DBE与△DFC中,
,
∴Rt△DBE≌Rt△DFC(HL),
∴∠B=∠DFC,
而图中∠B大小是固定的,∠DFC的大小随着F的变化而变化,故上述假设是不成立的,
故B选项错误;
(3)∵DC⊥AC,DE⊥AB,DC=DE,
利用角平分线的判定,
DC是∠BAC的平分线,
∴∠1=∠2,
故C选项正确;
(4)在直角三角形ABC中,利用斜边长度大于直角边长度,可以得到AB>AC,
故D选项错误,
故选:C.
2.解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:C.
3.解:根据题意得AB⊥BC,DE⊥CD,
∴∠ABC=∠EDC=90°,
∵CD=BC,∠ACB=∠ECD,
∴根据“ASA”可判断△EDC≌△ABC.
故选:A.
4.解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
故选:A.
5.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
6.解:如图①:
在△MCO和△NCO中,
,
∴△MCO≌△CNO(SSS),
∴∠AOC=∠BOC;
如图②,在Rt△MOP和Rt△NOP中,
,
∴Rt△MOP≌Rt△NOP(HL),
∴∠MOP=∠NOP,
即射线OP为∠AOB的角平分线.
故选:A.
7.解:在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS).
故选:C.
8.解:A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故本选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故本选项错误;
C、一条边对应相等,再加一组直角相等才能得出两三角形全等,故本选项错误;
D、当两个直角三角形的两直角边对应相等时,由ASA可以判定它们全等;当一直角边与一斜边对应相等时,由HL判定它们全等,故本选项正确;
故选:D.
9.解:∵AD=CF,
∴AC=DF,
∵∠F=∠ACB,
∴当添加BC=EF时,可根据”SAS“判断△ABC≌△DEF;
当添加∠A=∠EDF(或AB∥DE)时,可根据”ASA“判断△ABC≌△DEF;
当添加∠B=∠E时,可根据”AAS“判断△ABC≌△DEF.
故选:D.
10.解:如图,若∠1=∠2,则CD∥AB;
故选:C.
11.解:A图有两边相等,而夹角不一定相等,二者不一定全等;
B图与三角形ABC有两边及其夹角相等,二者全等;
C图有两边相等,而夹角不一定相等,二者不一定全等;
D图与三角形ABC有两角相等,二者不一定全等;
故选:B.
12.解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故选:B.
13.解:∵∠ACB=90°,
∴∠BCE+∠ACE=90°,
∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∠CAD+∠ACE=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE=2.5cm,BE=CD,
∵CD=CE﹣DE=2.5﹣1.7=0.8cm,
∴BE=0.8cm.
故选:B.
14.解:由题意可知:AB=CD.BC=AD,
∴四边形ABCD为平行四边形,
∴∠B+∠BCD=180°,
∴∠BCD=115°.
15.解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
16.解:如图,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
17.解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,如图所示:
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ADP=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
在△ABP与△ADP中,,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
∵△ABQ的周长为20,BP=4,
∴AB+BQ+AQ=AB+BP+AB=20,
∴AB=8;
故答案为:8.
18.解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
19.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
20.解:∵CF和BE相交于点O,
∴∠COB=∠EOF;(对顶角相等),
而O是CF的中点,那么CO=FO,又已知EO=BO,
∴△COB≌△FOE(SAS),
∴BC=EF,(全等三角形对应边相等),
∴∠BCO=∠F,(全等三角形的对应角相等),
∴AB∥DF,(内错角相等,两直线平行),
∴∠ACE和∠DEC互补.(两直线平行,同旁内角互补),
故答案为:对顶角相等,SAS,全等三角形的对应角相等,内错角相等,两直线平行,两直线平行,同旁内角互补.
21.解:(1)AE∥CF,AC∥DF,BC∥EF;
(2)AD=CF=BE=2cm;
(3)∵AE∥CF,∠ABC=65°,
∴∠BCF=∠ABC=65°.
22.解:(1)∠A=∠BCD,理由如下:
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB于点D,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD;
(2)△BOE≌△BOC,理由如下:
由(1)知,∠A=∠BCD,
∵OE∥AC,
∴∠A=∠OEB,
∴∠OEB=∠BCD=∠BCO,
∵BO平分∠DBC,
∴∠EBO=∠CBO,
在△BOE与△BOC中,
,
∴△BOE≌△BOC(AAS);
(3)由(2)知,△BOE≌△BOC,
∴BE=BC,
∵BC=5,
∴BE=5,
∵BC=5,AC=12,∠ACB=90°,
∴AB=13,
∴AE=AB﹣BE=8,
根据三角形的面积公式得到,?AB?CD=?AC?BC,
即×13?CD=×12×5,
∴CD=,
∴△ACE的面积为:?AE?CD=×8×=.
23.(1)证明:∵AD⊥CE,BE⊥CE,
∴∠D=∠E=90°,
在Rt△ACD和Rt△CBE中,
,
∴Rt△ACD≌Rt△CBE(HL),
∴∠DCA=∠EBC,
∵∠E=90°,
∴∠EBC+∠ECB=90°,
∴∠DCA+∠ECB=90°,
∴∠ACB=180°﹣90°=90°;
(2)解:△ODE等腰直角三角形,
理由如下:如图2,连接OC,
∵AC=BC,∠ACB=90°,点O是AB中点,
∴AO=BO=CO,∠CAB=∠CBA=45°,CO⊥AB,
∴∠AOC=∠BOC=∠ADC=∠BEC=90°,
∵∠BOC+∠BEC+∠ECO+∠EBO=360°,
∴∠EBO+∠ECO=180°,且∠DCO+∠ECO=180°,
∴∠DCO=∠EBO,
由(1)知,Rt△ACD≌Rt△CBE,
∴DC=BE,
在△DCO和△EBO中,
,
∴△DCO≌△EBO(SAS),
∴EO=DO,∠EOB=∠DOC,
∵∠COE+∠EOB=90°,
∴∠DOC+∠COE=90°,
∴∠DOE=90°,且DO=EO,
∴△ODE是等腰直角三角形.
一、选择题
1.如图,在△ABC中,∠C=90°,点D为BC上一点,DE⊥AB于E,并且DE=DC,F为AC上一点,则下列结论中正确的是( )
A.DE=DF
B.BD=FD
C.∠1=∠2
D.AB=AC
2.一块三角形玻璃样板不慎被张字同学碰破,成了四片完整碎片(如图所示),聪明的他经过仔细地考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为下列四个答案中考虑最全面的是( )
A.带1,2或2,3去就可以了
B.带1,4或3,4去就可以了
C.带1,4或2,4或3,4去均可
D.带其中的任意两块去都可以
3.如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是( )
A.ASA
B.SSS
C.AAS
D.SAS
4.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△EBD≌△ECD
D.以上答案都不对
5.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20°
B.40°
C.60°
D.70°
6.卞师傅用角尺平分一个角,如图①,学生小顾用三角尺平分一个角,如图②,他们在∠AOB两边上分别取OM=ON,前者使角尺两边相同刻度分别与M,N重合,角尺顶点为P;后者分别过M,N作OA,OB的垂线,交点为P,则射线OP平分∠AOB,均可由△OMP≌△ONP得知,其依据分别是( )
A.SSS;HL
B.SAS;HL
C.SSS;SAS
D.SAS;SSS
7.如图,在△ABC和△ABD中,已知AC=AD,BC=BD,则能说明△ABC≌△ABD的依据是( )
A.SAS
B.ASA
C.SSS
D.HL
8.使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.斜边及一条直角边对应相等
9.如图,点A,D,C,F在同一条直线上,AD=CF,∠F=∠ACB,再补充下列一个条件,不能证明△ABC≌△DEF的是( )
A.BC=EF
B.AB∥DE
C.∠B=∠E
D.AB=DE
10.如图,若∠1=∠2,则( )
A.AD∥BC
B.AD=BC
C.CD∥AB
D.AB=CD
11.如图所示,则下面图形中与图中△ABC一定全等的三角形是( )
A.B.C.D.
12.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8
B.7
C.6
D.5
13.如图,已知∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于点D,AD=2.5cm,DE=1.7cm,则BE=( )
A.1cm
B.0.8cm
C.4.2cm
D.1.5cm
二、填空题
如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD、CD.若∠B=65°,则∠BCD的大小
是
°.
15.在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE=
cm.
16.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画
个.
17.如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为
.
18.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=
.
19.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
三、解答题
20.如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他又没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补.请将小华的想法补充完整:
∵CF和BE相交于点O,
∴∠COB=∠EOF;(
)
而O是CF的中点,那么CO=FO,又已知EO=BO,
∴△COB≌△FOE,(
)
∴BC=EF,(全等三角形对应边相等)
∴∠BCO=∠F,(
)
∴AB∥DF,(
)
∴∠ACE和∠DEC互补.(
)
21.如图,将△ABC沿射线AB的方向移动2cm到△DEF的位置.
(1)找出图中所有平行的直线;
(2)找出图中与AD相等的线段,并写出其长度;
(3)若∠ABC=65°,求∠BCF的度数.
22.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BO平分∠DBC,交CD于点O,E为AB上一点,连接OE,且OE∥AC.
(1)∠A与∠BCD相等吗?请说明理由;
(2)△BOE与△BOC是否全等?为什么?
(3)若BC=5,AC=12,BD=,求出△ACE的面积.
23.已知,在△ABC中,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,且AD=CE.
(1)求证:∠ACB=90°;
(2)点O为AB的中点,连接OD,OE.请判断△ODE的形状?并说明理由.
参考答案
1.解:(1)在直角三角形DCF中,利用斜边长度大于直角边长度,可以得到DF>DC,又DC=DE,所以DF>DE,
故A选项错误;
(2)△BDE与△DCF,只满足∠DEB=∠DCF=90°,DC=DE的条件,不能判定两个三角形全等,故不能得到BD=FD,
另一方面,假设BD=FD,
在Rt△DBE与△DFC中,
,
∴Rt△DBE≌Rt△DFC(HL),
∴∠B=∠DFC,
而图中∠B大小是固定的,∠DFC的大小随着F的变化而变化,故上述假设是不成立的,
故B选项错误;
(3)∵DC⊥AC,DE⊥AB,DC=DE,
利用角平分线的判定,
DC是∠BAC的平分线,
∴∠1=∠2,
故C选项正确;
(4)在直角三角形ABC中,利用斜边长度大于直角边长度,可以得到AB>AC,
故D选项错误,
故选:C.
2.解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
带2、4可以延长还原出原三角形,
故选:C.
3.解:根据题意得AB⊥BC,DE⊥CD,
∴∠ABC=∠EDC=90°,
∵CD=BC,∠ACB=∠ECD,
∴根据“ASA”可判断△EDC≌△ABC.
故选:A.
4.解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
故选:A.
5.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
6.解:如图①:
在△MCO和△NCO中,
,
∴△MCO≌△CNO(SSS),
∴∠AOC=∠BOC;
如图②,在Rt△MOP和Rt△NOP中,
,
∴Rt△MOP≌Rt△NOP(HL),
∴∠MOP=∠NOP,
即射线OP为∠AOB的角平分线.
故选:A.
7.解:在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS).
故选:C.
8.解:A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故本选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故本选项错误;
C、一条边对应相等,再加一组直角相等才能得出两三角形全等,故本选项错误;
D、当两个直角三角形的两直角边对应相等时,由ASA可以判定它们全等;当一直角边与一斜边对应相等时,由HL判定它们全等,故本选项正确;
故选:D.
9.解:∵AD=CF,
∴AC=DF,
∵∠F=∠ACB,
∴当添加BC=EF时,可根据”SAS“判断△ABC≌△DEF;
当添加∠A=∠EDF(或AB∥DE)时,可根据”ASA“判断△ABC≌△DEF;
当添加∠B=∠E时,可根据”AAS“判断△ABC≌△DEF.
故选:D.
10.解:如图,若∠1=∠2,则CD∥AB;
故选:C.
11.解:A图有两边相等,而夹角不一定相等,二者不一定全等;
B图与三角形ABC有两边及其夹角相等,二者全等;
C图有两边相等,而夹角不一定相等,二者不一定全等;
D图与三角形ABC有两角相等,二者不一定全等;
故选:B.
12.解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故选:B.
13.解:∵∠ACB=90°,
∴∠BCE+∠ACE=90°,
∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∠CAD+∠ACE=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE=2.5cm,BE=CD,
∵CD=CE﹣DE=2.5﹣1.7=0.8cm,
∴BE=0.8cm.
故选:B.
14.解:由题意可知:AB=CD.BC=AD,
∴四边形ABCD为平行四边形,
∴∠B+∠BCD=180°,
∴∠BCD=115°.
15.解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
16.解:如图,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
17.解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,如图所示:
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ADP=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
在△ABP与△ADP中,,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
∵△ABQ的周长为20,BP=4,
∴AB+BQ+AQ=AB+BP+AB=20,
∴AB=8;
故答案为:8.
18.解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
19.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
20.解:∵CF和BE相交于点O,
∴∠COB=∠EOF;(对顶角相等),
而O是CF的中点,那么CO=FO,又已知EO=BO,
∴△COB≌△FOE(SAS),
∴BC=EF,(全等三角形对应边相等),
∴∠BCO=∠F,(全等三角形的对应角相等),
∴AB∥DF,(内错角相等,两直线平行),
∴∠ACE和∠DEC互补.(两直线平行,同旁内角互补),
故答案为:对顶角相等,SAS,全等三角形的对应角相等,内错角相等,两直线平行,两直线平行,同旁内角互补.
21.解:(1)AE∥CF,AC∥DF,BC∥EF;
(2)AD=CF=BE=2cm;
(3)∵AE∥CF,∠ABC=65°,
∴∠BCF=∠ABC=65°.
22.解:(1)∠A=∠BCD,理由如下:
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB于点D,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD;
(2)△BOE≌△BOC,理由如下:
由(1)知,∠A=∠BCD,
∵OE∥AC,
∴∠A=∠OEB,
∴∠OEB=∠BCD=∠BCO,
∵BO平分∠DBC,
∴∠EBO=∠CBO,
在△BOE与△BOC中,
,
∴△BOE≌△BOC(AAS);
(3)由(2)知,△BOE≌△BOC,
∴BE=BC,
∵BC=5,
∴BE=5,
∵BC=5,AC=12,∠ACB=90°,
∴AB=13,
∴AE=AB﹣BE=8,
根据三角形的面积公式得到,?AB?CD=?AC?BC,
即×13?CD=×12×5,
∴CD=,
∴△ACE的面积为:?AE?CD=×8×=.
23.(1)证明:∵AD⊥CE,BE⊥CE,
∴∠D=∠E=90°,
在Rt△ACD和Rt△CBE中,
,
∴Rt△ACD≌Rt△CBE(HL),
∴∠DCA=∠EBC,
∵∠E=90°,
∴∠EBC+∠ECB=90°,
∴∠DCA+∠ECB=90°,
∴∠ACB=180°﹣90°=90°;
(2)解:△ODE等腰直角三角形,
理由如下:如图2,连接OC,
∵AC=BC,∠ACB=90°,点O是AB中点,
∴AO=BO=CO,∠CAB=∠CBA=45°,CO⊥AB,
∴∠AOC=∠BOC=∠ADC=∠BEC=90°,
∵∠BOC+∠BEC+∠ECO+∠EBO=360°,
∴∠EBO+∠ECO=180°,且∠DCO+∠ECO=180°,
∴∠DCO=∠EBO,
由(1)知,Rt△ACD≌Rt△CBE,
∴DC=BE,
在△DCO和△EBO中,
,
∴△DCO≌△EBO(SAS),
∴EO=DO,∠EOB=∠DOC,
∵∠COE+∠EOB=90°,
∴∠DOC+∠COE=90°,
∴∠DOE=90°,且DO=EO,
∴△ODE是等腰直角三角形.
