《22.1.1二次函数》第一课时课件 2021-2022学年人教版九年级数学上册(27张PPT)
文档属性
| 名称 | 《22.1.1二次函数》第一课时课件 2021-2022学年人教版九年级数学上册(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 21:18:06 | ||
图片预览






文档简介
(共27张PPT)
二次函数的基本概念
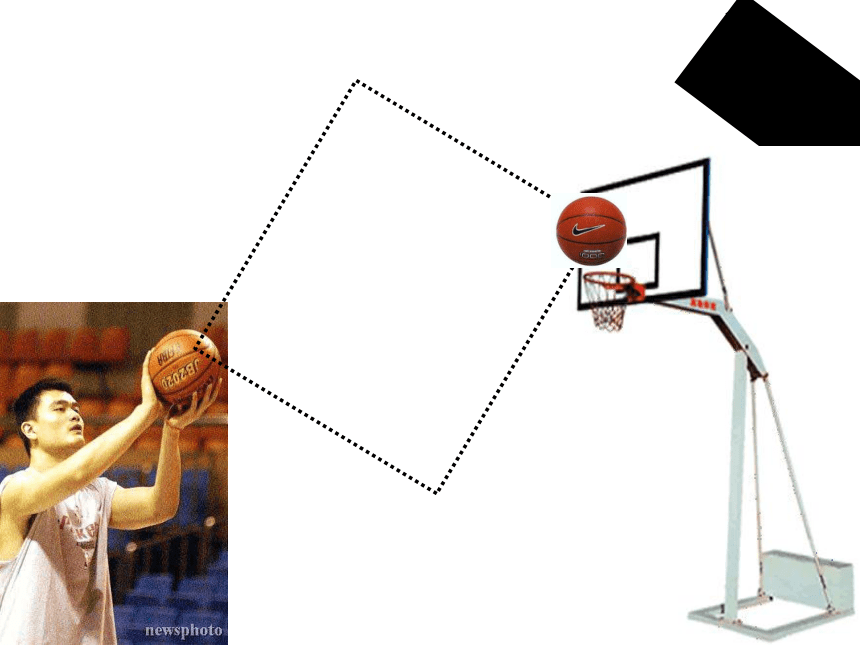
创设情境,导入新课
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
二次函数
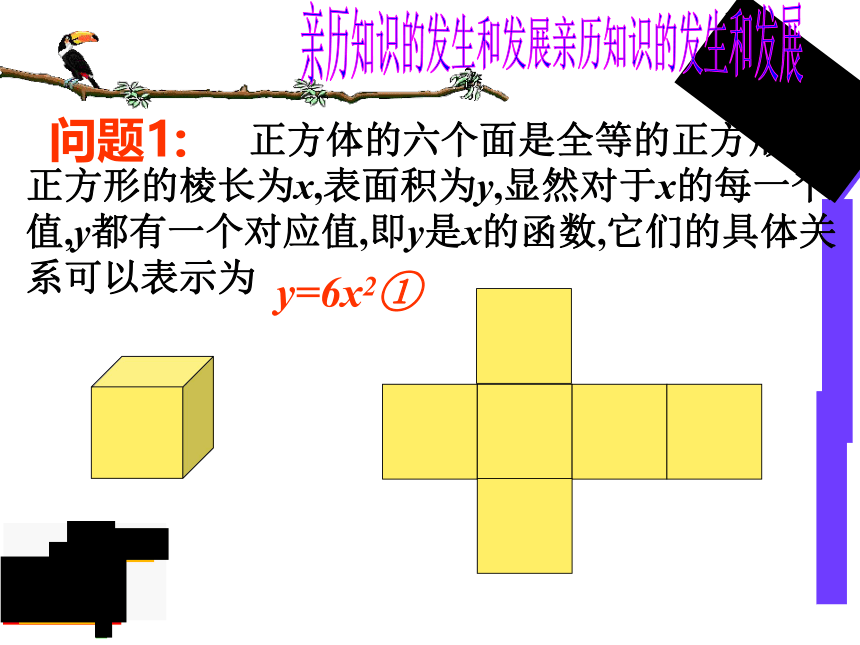
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题1:
y=6x2①
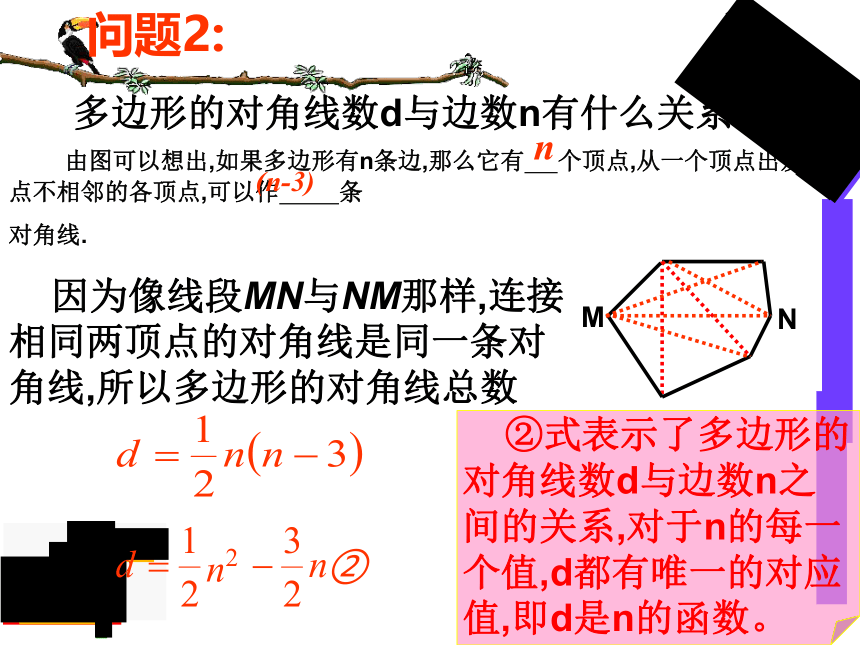
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作
条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有唯一的对应值,即d是n的函数。
问题3:某工厂一种产品现在的产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
这种产品的原产量是20件,一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量为
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数。
即
y=20(x+1)?
y=20x?+40x+20
③
20(1+x)
20(1+x)(1+x)
函数①②③有什么共同点?
观察:
y=6x2①
在上面的问题中,函数都是用自变量的二次式表示的。
2.
经化简后都具有y=ax?+bx+c
的形式.
(a,b,c是常数,
)
a≠0
合作学习,探索新知
:
(1)关系式都是整式,(2)自变量的最高次数是二次,(3)二次项系数不等于零
1.y=6x①
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
称:ax2叫做二次项,a为二次项系数
bx叫做一次项,
b为一次项系数
c为常数项,
二次函数的一般形式:
y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
1.下列函数中,哪些是二次函数?
展示自我,你行的
是
不是
是
不是
2、下列函数中,哪些是二次函数?
(
)
(
)
(
)
否
是
否
否
(
)
是
(
)
3.判断:下列函数是否为二次函数,如果是,指出其中常数a.b.c的值.
(1)
y=1—
(2)y=x(x-5)
(3)y=
x2-
x+1
(4)
y=3x(2-x)+
3x2
(5)y=
(6)
y=
(7)y=
x4+2x2-1
(8)y=ax2+bx+c
练一练:
1.一个圆柱的高等于底面半径,写出它的表面积
s
与半径
r
之间的关系式,是函数关系吗?是哪种函数?
2.
n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数
m与球队数
n
之间的关系式.
3.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
(A)
m,n是常数,且m≠0
(B)
m,n是常数,且n≠0
(C)
m,n是常数,且m≠n
(D)
m,n为任何实数
例1.若函数
为二次函数,求m的值。
解:因为
解(1)得:m=2或-1
解(2)得:
所以m=2
学海无涯:
牛刀小试
例2..已知二次函数
当x=1时,函数y有最小值为4
x取任意实数
(1)你能说出此函数的最小值吗?
(2)你能说出这里自变量能取哪些值呢?
牛刀小试:
关于x的函数
是二次函数,
求m的值.
解:
因为
注意:二次函数的二次项系数不能为零
想一想:例3
要用长20m的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为x,矩形的面积为y,试
(1)写出y关与x的函数关系式.
(2)当x=3时,距形的面积为多少?
(o如果函数y=
+kx+1是二次函数,
则k的值一定是______
如果函数y=(k-3)
+kx+1是二次函数,
则k的值一定是______
0
0或3
如果函数y=(k-3)
+kx+1
(x≠0)是一次
函数,则k的值一定是______
3或1或2
拓展与提高
一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。
xm
y
m2
xm
(40-2x
)m
解:
由题意得:
Y=x(40-2x)
即:Y=-2x2+40x
(0当x=12m时,菜园的面积为:
Y=-2x2+40x=-2×122+40×12
=192(m2)
思考:
二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
驶向胜利的彼岸
联系(1)等式一边都是ax2+bx+c且
a
≠0
(2)方程ax2+bx+c=0可以看成是函数y=
ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
这节课你有什么收获和体会?
回味无穷
小结
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)
y=ax?+bx(a≠0,b≠0,c=0).
(3)y=ax?+c(a≠0,b=0,c≠0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
二次函数的基本概念
创设情境,导入新课
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
二次函数
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题1:
y=6x2①
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作
条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有唯一的对应值,即d是n的函数。
问题3:某工厂一种产品现在的产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
这种产品的原产量是20件,一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量为
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数。
即
y=20(x+1)?
y=20x?+40x+20
③
20(1+x)
20(1+x)(1+x)
函数①②③有什么共同点?
观察:
y=6x2①
在上面的问题中,函数都是用自变量的二次式表示的。
2.
经化简后都具有y=ax?+bx+c
的形式.
(a,b,c是常数,
)
a≠0
合作学习,探索新知
:
(1)关系式都是整式,(2)自变量的最高次数是二次,(3)二次项系数不等于零
1.y=6x①
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
称:ax2叫做二次项,a为二次项系数
bx叫做一次项,
b为一次项系数
c为常数项,
二次函数的一般形式:
y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
1.下列函数中,哪些是二次函数?
展示自我,你行的
是
不是
是
不是
2、下列函数中,哪些是二次函数?
(
)
(
)
(
)
否
是
否
否
(
)
是
(
)
3.判断:下列函数是否为二次函数,如果是,指出其中常数a.b.c的值.
(1)
y=1—
(2)y=x(x-5)
(3)y=
x2-
x+1
(4)
y=3x(2-x)+
3x2
(5)y=
(6)
y=
(7)y=
x4+2x2-1
(8)y=ax2+bx+c
练一练:
1.一个圆柱的高等于底面半径,写出它的表面积
s
与半径
r
之间的关系式,是函数关系吗?是哪种函数?
2.
n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数
m与球队数
n
之间的关系式.
3.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
(A)
m,n是常数,且m≠0
(B)
m,n是常数,且n≠0
(C)
m,n是常数,且m≠n
(D)
m,n为任何实数
例1.若函数
为二次函数,求m的值。
解:因为
解(1)得:m=2或-1
解(2)得:
所以m=2
学海无涯:
牛刀小试
例2..已知二次函数
当x=1时,函数y有最小值为4
x取任意实数
(1)你能说出此函数的最小值吗?
(2)你能说出这里自变量能取哪些值呢?
牛刀小试:
关于x的函数
是二次函数,
求m的值.
解:
因为
注意:二次函数的二次项系数不能为零
想一想:例3
要用长20m的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为x,矩形的面积为y,试
(1)写出y关与x的函数关系式.
(2)当x=3时,距形的面积为多少?
(o
+kx+1是二次函数,
则k的值一定是______
如果函数y=(k-3)
+kx+1是二次函数,
则k的值一定是______
0
0或3
如果函数y=(k-3)
+kx+1
(x≠0)是一次
函数,则k的值一定是______
3或1或2
拓展与提高
一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。
xm
y
m2
xm
(40-2x
)m
解:
由题意得:
Y=x(40-2x)
即:Y=-2x2+40x
(0
Y=-2x2+40x=-2×122+40×12
=192(m2)
思考:
二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
驶向胜利的彼岸
联系(1)等式一边都是ax2+bx+c且
a
≠0
(2)方程ax2+bx+c=0可以看成是函数y=
ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
这节课你有什么收获和体会?
回味无穷
小结
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)
y=ax?+bx(a≠0,b≠0,c=0).
(3)y=ax?+c(a≠0,b=0,c≠0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
同课章节目录
