1.1.1空间向量及其线性运算(第一课时)课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修一第一册(共18张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算(第一课时)课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修一第一册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 17:32:44 | ||
图片预览





文档简介
(共18张PPT)
(第一课时)
1.1.1空间向量及其线性运算
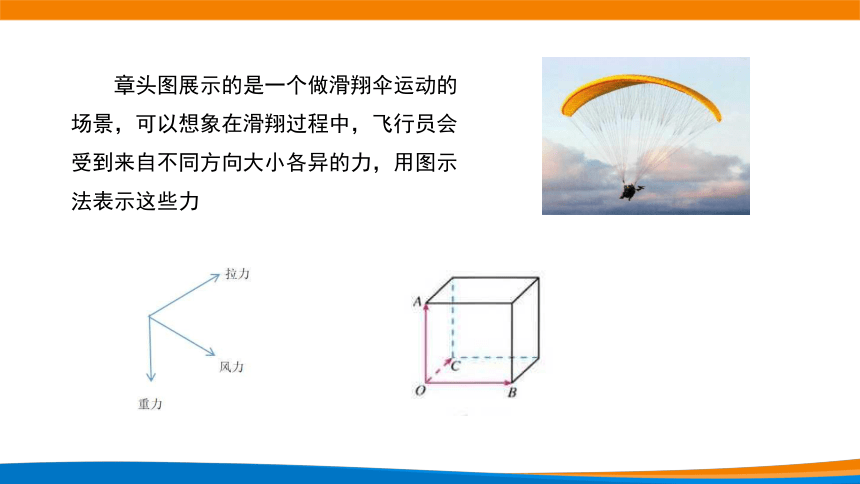
章头图展示的是一个做滑翔伞运动的场景,可以想象在滑翔过程中,飞行员会受到来自不同方向大小各异的力,用图示法表示这些力
1.
空间向量的概念:
具有大小和方向的量叫做空间向量.
2.
空间向量的表示:
一、新知探究:
A
B
3.
长度或模:
空间向量的大小,记为
4.
零向量:
长度为0的向量,记为
5.
单位向量:
一、新知探究:
6.
相反向量:
长度为1的向量.
与向量
长度相等,方向相反的向量,记为
一、新知探究:
方向相同且模相等的向量。
7、相等向量:
8.
共线向量:
如果表示若干空间向量的有向线段所在的直线互相平行或重合,这些向量叫共线向量或平行向量
规定:零向量与任意向量平行
√
×
×
×
练习
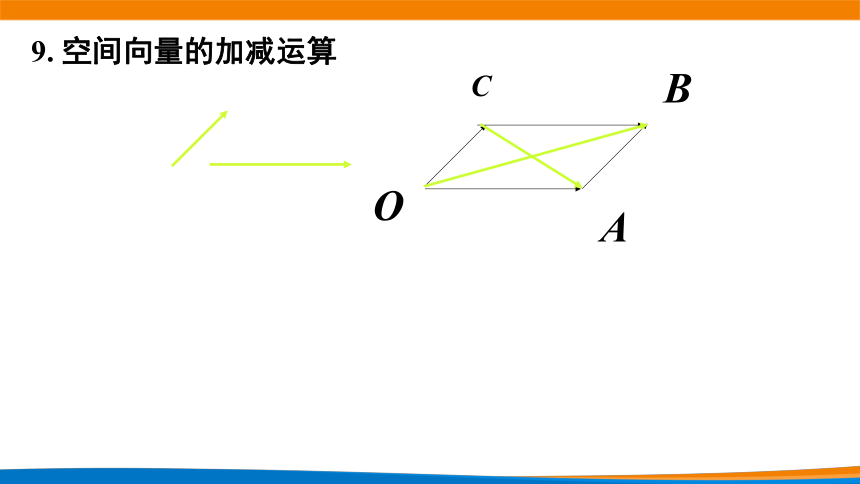
9.
空间向量的加减运算
A
B
C
O
10.
向量的数乘运算:
O
Q
A
P
O
M
A
N
11.
空间向量的加法与数乘向量运算律:
(1)
加法交换律:
(2)
加法结合律:
(3)
数乘分配律:
B
A
C
O
O●
A
B
C
推广:
O●
A
B
C
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。
A
B
C
D
A1
B1
C1
D1
G
M
探究:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量.(如图)
12.
向量共线定理
12.
方向向量
P
O
l
13.
共面向量
O
l
A
14.
向量共面定理
A、B、P三点共线
P与A,B,C共面
小结
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
5、共线向量与共面向量
再会!
(第一课时)
1.1.1空间向量及其线性运算
章头图展示的是一个做滑翔伞运动的场景,可以想象在滑翔过程中,飞行员会受到来自不同方向大小各异的力,用图示法表示这些力
1.
空间向量的概念:
具有大小和方向的量叫做空间向量.
2.
空间向量的表示:
一、新知探究:
A
B
3.
长度或模:
空间向量的大小,记为
4.
零向量:
长度为0的向量,记为
5.
单位向量:
一、新知探究:
6.
相反向量:
长度为1的向量.
与向量
长度相等,方向相反的向量,记为
一、新知探究:
方向相同且模相等的向量。
7、相等向量:
8.
共线向量:
如果表示若干空间向量的有向线段所在的直线互相平行或重合,这些向量叫共线向量或平行向量
规定:零向量与任意向量平行
√
×
×
×
练习
9.
空间向量的加减运算
A
B
C
O
10.
向量的数乘运算:
O
Q
A
P
O
M
A
N
11.
空间向量的加法与数乘向量运算律:
(1)
加法交换律:
(2)
加法结合律:
(3)
数乘分配律:
B
A
C
O
O●
A
B
C
推广:
O●
A
B
C
(1)首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量。
A
B
C
D
A1
B1
C1
D1
G
M
探究:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量.(如图)
12.
向量共线定理
12.
方向向量
P
O
l
13.
共面向量
O
l
A
14.
向量共面定理
A、B、P三点共线
P与A,B,C共面
小结
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
5、共线向量与共面向量
再会!
