3.2.1双曲线及其标准方程(第二课时)课件-2021-2022学年高二上学期人教A版(2019)数学选择性必修一第一册(共15张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程(第二课时)课件-2021-2022学年高二上学期人教A版(2019)数学选择性必修一第一册(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 633.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
(第二课时)
3.2.1双曲线及其标准方程
双曲线的定义是什么?
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
问题1
问题2
平面内与两个定点F1,F2的距离的差的绝对值等于常数(记为2a)的点的轨迹是双曲线吗?
(4)
若2a=0,则轨迹是什么?
(3)
若2a>2c,则轨迹是什么?
(2)
若2a=2c,则轨迹是什么?
两条射线
不存在
线段F1F2的垂直平分线
(1)
若2a<2c,则轨迹是什么?
双曲线
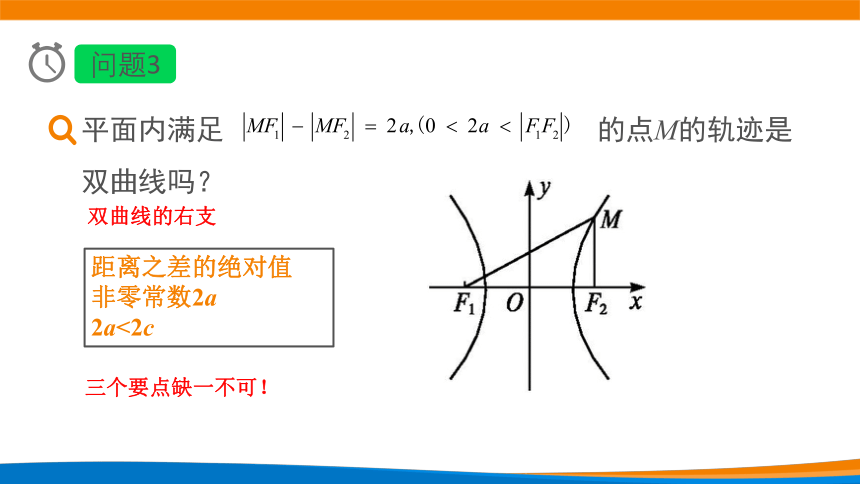
问题3
平面内满足
的点M的轨迹是双曲线吗?
双曲线的右支
距离之差的绝对值
非零常数2a
2a<2c
三个要点缺一不可!
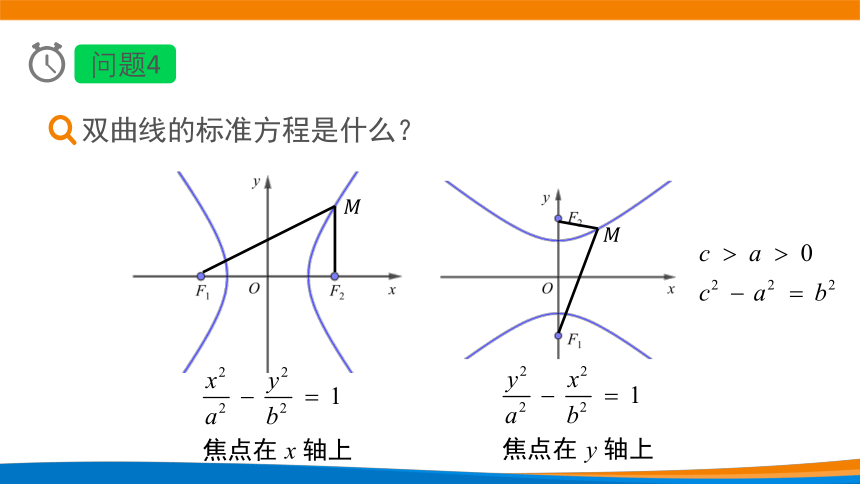
问题4
双曲线的标准方程是什么?
例题1
例题2
求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,
,经过点A(-5,2);
例题2
求适合下列条件的双曲线的标准方程.
(2)过点(1,1),且
例题2
求适合下列条件的双曲线的标准方程.
(3)经过两点.
求双曲线的标准方程与求椭圆的标准方程的方法相似,可以先根据其焦点位置设出标准方程,然后用待定系数法求出a,b的值.若焦点位置不确定,可按焦点在x轴和y轴上两种情况讨论求解,此方法思路清晰,但过程复杂.若双曲线过两定点,可设其方程为mx2+ny2=1(mn<0),通过解方程组即可确定m,n,避免了讨论,从而简化求解过程.
问题5
例题3
A.(-1,+∞)
B.(2,+∞)
C.(-∞,-1)∪(2,+∞)
D.(-1,2)
解得-1答案:D
问题6
“神舟”九号飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方位角.
解:因为|PC|=|PB|,所以P在线段BC的垂直平分线上.
又因为|PB|-|PA|=4<6=|AB|,
所以P在以A,B为焦点的双曲线的右支上.
问题6
以线段AB的中点为坐标原点,AB的垂直平分线所在直线为y轴,正东方向为x轴正方向建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,
).
|PB|-|PA|=4
本节小结
再会!
(第二课时)
3.2.1双曲线及其标准方程
双曲线的定义是什么?
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
问题1
问题2
平面内与两个定点F1,F2的距离的差的绝对值等于常数(记为2a)的点的轨迹是双曲线吗?
(4)
若2a=0,则轨迹是什么?
(3)
若2a>2c,则轨迹是什么?
(2)
若2a=2c,则轨迹是什么?
两条射线
不存在
线段F1F2的垂直平分线
(1)
若2a<2c,则轨迹是什么?
双曲线
问题3
平面内满足
的点M的轨迹是双曲线吗?
双曲线的右支
距离之差的绝对值
非零常数2a
2a<2c
三个要点缺一不可!
问题4
双曲线的标准方程是什么?
例题1
例题2
求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,
,经过点A(-5,2);
例题2
求适合下列条件的双曲线的标准方程.
(2)过点(1,1),且
例题2
求适合下列条件的双曲线的标准方程.
(3)经过两点.
求双曲线的标准方程与求椭圆的标准方程的方法相似,可以先根据其焦点位置设出标准方程,然后用待定系数法求出a,b的值.若焦点位置不确定,可按焦点在x轴和y轴上两种情况讨论求解,此方法思路清晰,但过程复杂.若双曲线过两定点,可设其方程为mx2+ny2=1(mn<0),通过解方程组即可确定m,n,避免了讨论,从而简化求解过程.
问题5
例题3
A.(-1,+∞)
B.(2,+∞)
C.(-∞,-1)∪(2,+∞)
D.(-1,2)
解得-1
问题6
“神舟”九号飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方位角.
解:因为|PC|=|PB|,所以P在线段BC的垂直平分线上.
又因为|PB|-|PA|=4<6=|AB|,
所以P在以A,B为焦点的双曲线的右支上.
问题6
以线段AB的中点为坐标原点,AB的垂直平分线所在直线为y轴,正东方向为x轴正方向建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,
).
|PB|-|PA|=4
本节小结
再会!
