2.3变量间的相关关系
图片预览










文档简介
(共66张PPT)
变量间的相关关系
2.3
2.3.1 变量之间的相关关系
2.3.2(1) 两个变量的线性相关
2.3.2(2) 两个变量的线性相关-回归直线
2.3 变量间的相关关系
2.3.1 变量之间的相关关系
2.3.2(1) 两个变量的线性相关
(A)
(B)
(C)
(D)
A
B
D
C
1、下列各情景分别可以用哪一幅图来近似的刻画
(1)汽车紧急刹车(速度与时间的关系)
(2)人的身高变化(身高与年龄的关系)
(3)跳高运动员跳跃横杆(高度与时间的关系)
(4)一面冉冉上升的红旗(高度与时间的关系)
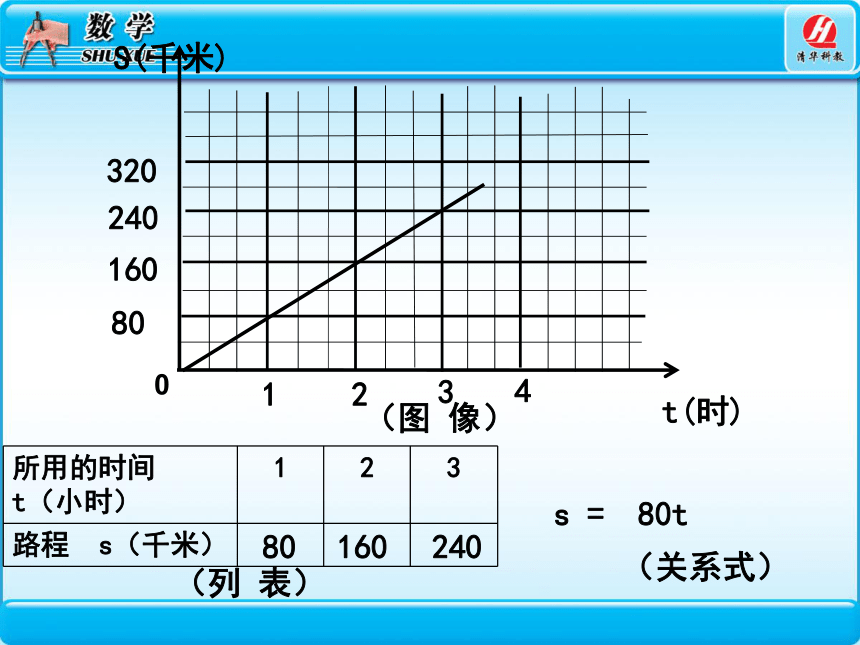
2、在一条高速公路上,一辆轿车以80千米/时的速度匀速行驶.随着时间t 的变化汽车行驶的路程s也相应发生着变化.
t(时)
1
3
2
4
80
240
160
320
S(千米)
(列 表)
所用的时间
t(小时) 1 2 3
路程 s(千米)
s = 80t
(图 像)
(关系式)
80
240
160
0
函数是研究两个变量之间的依存关系的一种数量形式.对于两个变量,如果当一个变量的取值一定时,另一个变量的取值被惟一确定,则这两个变量之间的关系就是一个函数关系.
思考:在中学校园里,有这样一种说法:“如果你的数学成绩好,那么你的物理学习就不会有什么大问题.”按照这种说法,似乎学生的物理成绩与数学成绩之间存在着某种相关关系,这种说法有没有根据呢?
请同学们如实填写下表(在空格中打“√” )
讨论数学成绩与物理成绩的关系.
好 中 差
数学成绩
物理成绩
我们可以发现自己的数学成绩和物理成绩存在某种关系.(似乎就是数学好的,物理也好;数学差的,物理也差,但又不全对.)物理成绩和数学成绩是两个变量,从经验看,由于物理学习要用到比较多的数学知识和数学方法.数学成绩的高低对物理成绩的高低是有一定影响的.但决非唯一因素,还有其它因素,如是否喜欢物理,用在物理学习上的时间等等.
总结:不能通过一个人的数学成绩是多少就准确地断定他的物理成绩能达到多少.但这两个变量是有一定关系的,它们之间是一种不确定性的关系.如何通过数学成绩的结果对物理成绩进行合理估计有非常重要的现实意义.
不是函数关系,但这两个变量是有一定关系的,当我们主要考察数学成绩对物理成绩的影响时,就是要考察这两者之间的相关关系.
这两个变量是函数关系吗?
练习1:考察下列问题中两个变量之间的关系:
(1)商品销售收入与广告支出经费;
(2)粮食产量与施肥量;
(3)人体内的脂肪含量与年龄.
这些问题中两个变量之间的关系是函数关系吗?
(1)商品销售收入与广告支出经费之间的关系.商品销售收入与广告支出经费有着密切的联系,但商品销售收入不仅与广告支出多少有关,还与商品质量, 居民收入,生活环境等因素有关.
(2)粮食产量与施肥量之间的关系.在一定范围内,施肥量越大,粮食产量就越高.但是,施肥量并不是决定粮食产量的唯一因素,因为粮食产量还要受到土壤质量,降雨量,田间管理水平等因素的影响.
(3)人体内的脂肪含量与年龄之间的关系.在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯,体育锻炼等有关,可能还与个人的先天体质有关.
练习2:“名师出高徒”可以解释为教师的水平越高,学生的水平就越高,那么学生的学业成绩与教师的教学水平之间的关系是函数关系吗?你能举出类似的描述生活中两个变量之间的这种关系的成语吗?
两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系.上述两个变量之间的关系是一种非确定性关系,称之为相关关系.
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系.相关关系是一种非确定性关系.
两个变量→
自变量取值一定→
因变量带有随机性→
相关关系
相关关系的概念:
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
不同点:函数关系是一种确定的关系;而相关关系是一种非确定关系.
对于一个变量,可以控制其数量大小的变量称为可控变量,否则称为随机变量,那么相关关系中的两个变量有哪几种类型?
(1)一个为可控变量,另一个为随机变量;
(2)两个都是随机变量.
练习3:有关法律规定,香烟盒上必须印上“吸烟有害健康”的警示语.吸烟是否一定会引起健康问题?你认为“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法对吗?
答:从已经掌握的知识来看 ,吸烟会损害身体的健康.但是除了吸烟之外,还有许多其它的随机因素影响身体健康,人体健康是有很多因素共同作用的结果.我们可以找到长寿的吸烟者,也更容易发现由于吸烟而引发的患病者,所以吸烟不一定引起健康问题.但吸烟引起健康问题的可能性大,因此“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法是不对的.
练习4:某地区的环境条件适合天鹅栖息繁衍,有人统计发现了一个非常有趣的现象,如果村庄附近栖息的天鹅多,那么这个村庄的婴儿出生率也高,天鹅少的地方婴儿的出生率低.于是,他就得出一个结论:天鹅能够带来孩子,你认为这样得到的结论可靠吗?如何证明这个结论的可靠性?
答:从现在我们掌握的知识来看,没有发现根据说明“天鹅能够带来孩子”,完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素(例如独特的环境因素),即天鹅与婴儿出生率之间没有直接的关系,因此“天鹅能够带来孩子”的结论不可靠.
而要证实此结论是否可靠,可以通过实验来进行.相同的环境下将居民随机地分为两组,一组居民和天鹅一起生活(比如家中都饲养天鹅),而另一组居民的附近不让天鹅活动,对比两组居民的出生率是否相同.
探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
对某一个人来说,他的体内脂肪含量不一定随年龄增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.
观察上表中的数据,大体上看,随着年龄的增加,人体脂肪含量怎样变化?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析.
与以前一样,我们可以通过作统计图、表,使我们对两个变量之间的关系有一个直观的印象和判断.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析.
通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
下图叫做散点图,你能描述一下散点图的含义吗?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
计算机可以帮助我们作散点图.下图就是用计算机作出来的.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
观察散点图的大致趋势,人的年龄与人体脂肪含量具有什么相关关系?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
从散点图可以看出,年龄越大,体内脂肪含量越高.
这个图支持了我们从数据表中得出的结论.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
在上面的散点图中,这些点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
一般地,如果两个变量成正相关,那么这两个变量的变化趋势如何?
思考1:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?
一个变量随另一个变量的变大而变小.
思考3:你能列举一些生活中的变量成正相关或负相关的实例吗
思考2:其散点图有什么特点?
散点图中的点散布在从左上角到右下角的区域.
练习1:在下列两个变量的关系中,哪些是相关关系?
⑴汽车行驶路程与速度之间的关系;
⑵作文水平与课外阅读量之间的关系;
⑶人的身高与年龄之间的关系;
⑷吸烟与癌症的发生率之间的关系.
练习2: 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了7次试验,收集数据如下:
零件数x(个) 10 20 30 40 50 60 70
加工时间y(min) 62 68 75 81 95 102 108
画出数据对应的散点图,并指出销售价格与房屋面积这两个变量是正相关还是负相关.
1、对于两个变量之间的关系,有函数关系和相关关系两种,其中函数关系是一种确定性关系,相关关系是一种非确定性关系.
3、散点图能直观反映两个相关变量之间的大致变化趋势,可用来判断两个变量之间的相关关系成正相关或负相关.
2、散点图的作法及正、负相关的概念.
小结
布置作业:
P94练习:2(1)、3(1)、4(1) .
2.3.2(2) 两个变量的线性相关
-回归直线
当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系.相关关系是一种非确定性关系.
2、相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
不同点:函数关系是一种确定的关系;而相关关系是一种非确定关系.
1、相关关系的概念:
3、在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
正相关的散点图中的点散布在从左下角到右上角的区域,负相关的散点图中的点散布在从左上角到右下角的区域
4、成正相关和负相关的两个相关变量的散点图分别有什么特点?
探究:观察人体的脂肪含量百分比和年龄的样本数据的散点图,这两个相关变量成正相关.我们需要进一步考虑的问题是,当人的年龄增加时,体内脂肪含量到底是以什么方式增加呢?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
讨论:有些散点图中的点是杂乱分布的,有些散点图中的点的分布有一定的规律性,年龄和人体脂肪含量的样本数据的散点图中的点的分布有什么特点?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
这些点大致分布在一条直线附近.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
如果散点图中的点的分布,从整体上看大致在一条直线附近,则称这两个变量之间具有线性相关关系,这条直线叫做回归直线.并根据回归方程对总体进行估计.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
讨论:1、每个同学画的直线相同吗?
2、你认为回归直线有很多条吗?
3、你可以求出直线方程吗?
大家的建议都有一定的道理,但总让人感到可靠性不强.
回归直线与散点图中各点的位置用数学的方法来刻画应具有怎样的关系?
从整体上看,各点与此直线最接近,距离最小.
你能解释这句话的含义吗?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
讨论:对一组具有线性相关关系的样本数据:
(x1,y1),(x2,y2),…,(xn,yn),
设其回归方程为 ,可以用哪些数量关
系来刻画各样本点与回归直线的接近程度?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
我们可以用点(xi,yi)与这条直线上横坐标为xi的点之间的距离来刻画点(xi,yi)到直线的远近.
为了从整体上反映n个样本数据与回归直线的接近程度,你认为选用哪个数量关系来刻画比较合适?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
用这n个距离之和来刻画各点到直线的“整体距离”是比较合适的,即可以用
表示各点到直线 的“整体距离”.
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
用这n个距离之和来刻画各点到直线的“整体距离”是比较合适的,即可以用
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
由于绝对值使得计算不方便,在实际应用中人们更喜欢用
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
这样,问题就归结为:当a,b取什么值时Q最小?即点到直线 的“整体距离”最小.
这样,问题就归结为:当a,b取什么值时Q最小?即点到直线 的“整体距离”最小.
这样通过求此式的最小值而得到回归直线的方法,即使得一半数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
根据有关数学原理推导,a,b的值由下列公式给出
根据最小二乘法的思想和此公式,利用计算器或计算机可以方便的求得年龄和人体脂肪含量的样本数据的回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
⑴在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
⑵单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
⑶双击回归直线,弹出“趋势线格式”对话框“.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程.
试一试:将表中的年龄作为x代入上述方程,看看得出的数值与真实数值之间的关系,从中你体会到什么?
利用回归直线,我们可以进行预测.
例:为了研究三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)的关系,某地区观察了1996年至2001年的情况,得到下面的数据 :
年份 1996 1997 1998 1999 2000 2001
X(oC) 24.4 29.6 32.9 28.7 30.3 28.9
Y(天) 19 6 1 10 1 8
(1)画出散点图;
(2)从散点图中发现三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)之 间关系的一般规律;
(3)求回归方程;
(4)该地区在2002年三月下旬平均气温为27℃,试估计2002年四月化蛹高峰日为几天.
年份 1996 1997 1998 1999 2000 2001
X(oC) 24.4 29.6 32.9 28.7 30.3 28.9
Y(天) 19 6 1 10 1 8
小结
1、求样本数据的线性回归方程,可按下列步骤进行:
第一步,计算平均数 ,
第二步,求和 ,
第三步,计算
第四步,写出回归方程
2、回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性.
3、对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.如果一组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.
布置作业:
P94习题2.3 A组:2,3.
B组:1.
变量间的相关关系
2.3
2.3.1 变量之间的相关关系
2.3.2(1) 两个变量的线性相关
2.3.2(2) 两个变量的线性相关-回归直线
2.3 变量间的相关关系
2.3.1 变量之间的相关关系
2.3.2(1) 两个变量的线性相关
(A)
(B)
(C)
(D)
A
B
D
C
1、下列各情景分别可以用哪一幅图来近似的刻画
(1)汽车紧急刹车(速度与时间的关系)
(2)人的身高变化(身高与年龄的关系)
(3)跳高运动员跳跃横杆(高度与时间的关系)
(4)一面冉冉上升的红旗(高度与时间的关系)
2、在一条高速公路上,一辆轿车以80千米/时的速度匀速行驶.随着时间t 的变化汽车行驶的路程s也相应发生着变化.
t(时)
1
3
2
4
80
240
160
320
S(千米)
(列 表)
所用的时间
t(小时) 1 2 3
路程 s(千米)
s = 80t
(图 像)
(关系式)
80
240
160
0
函数是研究两个变量之间的依存关系的一种数量形式.对于两个变量,如果当一个变量的取值一定时,另一个变量的取值被惟一确定,则这两个变量之间的关系就是一个函数关系.
思考:在中学校园里,有这样一种说法:“如果你的数学成绩好,那么你的物理学习就不会有什么大问题.”按照这种说法,似乎学生的物理成绩与数学成绩之间存在着某种相关关系,这种说法有没有根据呢?
请同学们如实填写下表(在空格中打“√” )
讨论数学成绩与物理成绩的关系.
好 中 差
数学成绩
物理成绩
我们可以发现自己的数学成绩和物理成绩存在某种关系.(似乎就是数学好的,物理也好;数学差的,物理也差,但又不全对.)物理成绩和数学成绩是两个变量,从经验看,由于物理学习要用到比较多的数学知识和数学方法.数学成绩的高低对物理成绩的高低是有一定影响的.但决非唯一因素,还有其它因素,如是否喜欢物理,用在物理学习上的时间等等.
总结:不能通过一个人的数学成绩是多少就准确地断定他的物理成绩能达到多少.但这两个变量是有一定关系的,它们之间是一种不确定性的关系.如何通过数学成绩的结果对物理成绩进行合理估计有非常重要的现实意义.
不是函数关系,但这两个变量是有一定关系的,当我们主要考察数学成绩对物理成绩的影响时,就是要考察这两者之间的相关关系.
这两个变量是函数关系吗?
练习1:考察下列问题中两个变量之间的关系:
(1)商品销售收入与广告支出经费;
(2)粮食产量与施肥量;
(3)人体内的脂肪含量与年龄.
这些问题中两个变量之间的关系是函数关系吗?
(1)商品销售收入与广告支出经费之间的关系.商品销售收入与广告支出经费有着密切的联系,但商品销售收入不仅与广告支出多少有关,还与商品质量, 居民收入,生活环境等因素有关.
(2)粮食产量与施肥量之间的关系.在一定范围内,施肥量越大,粮食产量就越高.但是,施肥量并不是决定粮食产量的唯一因素,因为粮食产量还要受到土壤质量,降雨量,田间管理水平等因素的影响.
(3)人体内的脂肪含量与年龄之间的关系.在一定年龄段内,随着年龄的增长,人体内的脂肪含量会增加,但人体内的脂肪含量还与饮食习惯,体育锻炼等有关,可能还与个人的先天体质有关.
练习2:“名师出高徒”可以解释为教师的水平越高,学生的水平就越高,那么学生的学业成绩与教师的教学水平之间的关系是函数关系吗?你能举出类似的描述生活中两个变量之间的这种关系的成语吗?
两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系.上述两个变量之间的关系是一种非确定性关系,称之为相关关系.
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系.相关关系是一种非确定性关系.
两个变量→
自变量取值一定→
因变量带有随机性→
相关关系
相关关系的概念:
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
不同点:函数关系是一种确定的关系;而相关关系是一种非确定关系.
对于一个变量,可以控制其数量大小的变量称为可控变量,否则称为随机变量,那么相关关系中的两个变量有哪几种类型?
(1)一个为可控变量,另一个为随机变量;
(2)两个都是随机变量.
练习3:有关法律规定,香烟盒上必须印上“吸烟有害健康”的警示语.吸烟是否一定会引起健康问题?你认为“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法对吗?
答:从已经掌握的知识来看 ,吸烟会损害身体的健康.但是除了吸烟之外,还有许多其它的随机因素影响身体健康,人体健康是有很多因素共同作用的结果.我们可以找到长寿的吸烟者,也更容易发现由于吸烟而引发的患病者,所以吸烟不一定引起健康问题.但吸烟引起健康问题的可能性大,因此“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法是不对的.
练习4:某地区的环境条件适合天鹅栖息繁衍,有人统计发现了一个非常有趣的现象,如果村庄附近栖息的天鹅多,那么这个村庄的婴儿出生率也高,天鹅少的地方婴儿的出生率低.于是,他就得出一个结论:天鹅能够带来孩子,你认为这样得到的结论可靠吗?如何证明这个结论的可靠性?
答:从现在我们掌握的知识来看,没有发现根据说明“天鹅能够带来孩子”,完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素(例如独特的环境因素),即天鹅与婴儿出生率之间没有直接的关系,因此“天鹅能够带来孩子”的结论不可靠.
而要证实此结论是否可靠,可以通过实验来进行.相同的环境下将居民随机地分为两组,一组居民和天鹅一起生活(比如家中都饲养天鹅),而另一组居民的附近不让天鹅活动,对比两组居民的出生率是否相同.
探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
探究:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
对某一个人来说,他的体内脂肪含量不一定随年龄增长而增加或减少,但是如果把很多个体放在一起,就可能表现出一定的规律性.
观察上表中的数据,大体上看,随着年龄的增加,人体脂肪含量怎样变化?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析.
与以前一样,我们可以通过作统计图、表,使我们对两个变量之间的关系有一个直观的印象和判断.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析.
通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
下图叫做散点图,你能描述一下散点图的含义吗?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
计算机可以帮助我们作散点图.下图就是用计算机作出来的.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
观察散点图的大致趋势,人的年龄与人体脂肪含量具有什么相关关系?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
从散点图可以看出,年龄越大,体内脂肪含量越高.
这个图支持了我们从数据表中得出的结论.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
在上面的散点图中,这些点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
一般地,如果两个变量成正相关,那么这两个变量的变化趋势如何?
思考1:如果两个变量成负相关,从整体上看这两个变量的变化趋势如何?
一个变量随另一个变量的变大而变小.
思考3:你能列举一些生活中的变量成正相关或负相关的实例吗
思考2:其散点图有什么特点?
散点图中的点散布在从左上角到右下角的区域.
练习1:在下列两个变量的关系中,哪些是相关关系?
⑴汽车行驶路程与速度之间的关系;
⑵作文水平与课外阅读量之间的关系;
⑶人的身高与年龄之间的关系;
⑷吸烟与癌症的发生率之间的关系.
练习2: 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了7次试验,收集数据如下:
零件数x(个) 10 20 30 40 50 60 70
加工时间y(min) 62 68 75 81 95 102 108
画出数据对应的散点图,并指出销售价格与房屋面积这两个变量是正相关还是负相关.
1、对于两个变量之间的关系,有函数关系和相关关系两种,其中函数关系是一种确定性关系,相关关系是一种非确定性关系.
3、散点图能直观反映两个相关变量之间的大致变化趋势,可用来判断两个变量之间的相关关系成正相关或负相关.
2、散点图的作法及正、负相关的概念.
小结
布置作业:
P94练习:2(1)、3(1)、4(1) .
2.3.2(2) 两个变量的线性相关
-回归直线
当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系.相关关系是一种非确定性关系.
2、相关关系与函数关系的异同点:
相同点:均是指两个变量的关系.
不同点:函数关系是一种确定的关系;而相关关系是一种非确定关系.
1、相关关系的概念:
3、在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
正相关的散点图中的点散布在从左下角到右上角的区域,负相关的散点图中的点散布在从左上角到右下角的区域
4、成正相关和负相关的两个相关变量的散点图分别有什么特点?
探究:观察人体的脂肪含量百分比和年龄的样本数据的散点图,这两个相关变量成正相关.我们需要进一步考虑的问题是,当人的年龄增加时,体内脂肪含量到底是以什么方式增加呢?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
讨论:有些散点图中的点是杂乱分布的,有些散点图中的点的分布有一定的规律性,年龄和人体脂肪含量的样本数据的散点图中的点的分布有什么特点?
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
这些点大致分布在一条直线附近.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
如果散点图中的点的分布,从整体上看大致在一条直线附近,则称这两个变量之间具有线性相关关系,这条直线叫做回归直线.并根据回归方程对总体进行估计.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
如果能够求出这条回归直线的方程(简称回归方程),那么我们就可以比较清楚地了解年龄与体内脂肪含量的相关性.
20
40
30
50
10
30
20
40
脂肪含量)
60
0
10
年龄
讨论:1、每个同学画的直线相同吗?
2、你认为回归直线有很多条吗?
3、你可以求出直线方程吗?
大家的建议都有一定的道理,但总让人感到可靠性不强.
回归直线与散点图中各点的位置用数学的方法来刻画应具有怎样的关系?
从整体上看,各点与此直线最接近,距离最小.
你能解释这句话的含义吗?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
讨论:对一组具有线性相关关系的样本数据:
(x1,y1),(x2,y2),…,(xn,yn),
设其回归方程为 ,可以用哪些数量关
系来刻画各样本点与回归直线的接近程度?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
我们可以用点(xi,yi)与这条直线上横坐标为xi的点之间的距离来刻画点(xi,yi)到直线的远近.
为了从整体上反映n个样本数据与回归直线的接近程度,你认为选用哪个数量关系来刻画比较合适?
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
用这n个距离之和来刻画各点到直线的“整体距离”是比较合适的,即可以用
表示各点到直线 的“整体距离”.
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
用这n个距离之和来刻画各点到直线的“整体距离”是比较合适的,即可以用
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
由于绝对值使得计算不方便,在实际应用中人们更喜欢用
(x1,y1)
(x2,y2)
(xi,yi)
(xn,yn)
这样,问题就归结为:当a,b取什么值时Q最小?即点到直线 的“整体距离”最小.
这样,问题就归结为:当a,b取什么值时Q最小?即点到直线 的“整体距离”最小.
这样通过求此式的最小值而得到回归直线的方法,即使得一半数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
根据有关数学原理推导,a,b的值由下列公式给出
根据最小二乘法的思想和此公式,利用计算器或计算机可以方便的求得年龄和人体脂肪含量的样本数据的回归方程.
以Excel软件为例,用散点图来建立表示人体的脂肪含量与年龄的相关关系的线性回归方程,具体步骤如下:
⑴在Excel中选定表示人体的脂肪含量与年龄的相关关系的散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框.
⑵单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
⑶双击回归直线,弹出“趋势线格式”对话框“.单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程.
试一试:将表中的年龄作为x代入上述方程,看看得出的数值与真实数值之间的关系,从中你体会到什么?
利用回归直线,我们可以进行预测.
例:为了研究三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)的关系,某地区观察了1996年至2001年的情况,得到下面的数据 :
年份 1996 1997 1998 1999 2000 2001
X(oC) 24.4 29.6 32.9 28.7 30.3 28.9
Y(天) 19 6 1 10 1 8
(1)画出散点图;
(2)从散点图中发现三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)之 间关系的一般规律;
(3)求回归方程;
(4)该地区在2002年三月下旬平均气温为27℃,试估计2002年四月化蛹高峰日为几天.
年份 1996 1997 1998 1999 2000 2001
X(oC) 24.4 29.6 32.9 28.7 30.3 28.9
Y(天) 19 6 1 10 1 8
小结
1、求样本数据的线性回归方程,可按下列步骤进行:
第一步,计算平均数 ,
第二步,求和 ,
第三步,计算
第四步,写出回归方程
2、回归方程被样本数据惟一确定,各样本点大致分布在回归直线附近.对同一个总体,不同的样本数据对应不同的回归直线,所以回归直线也具有随机性.
3、对一组样本数据,应先作散点图,在具有线性相关关系的前提下再求回归方程.如果一组数据不具有线性相关关系,即不存在回归直线,那么所得的“回归方程”是没有实际意义的.
布置作业:
P94习题2.3 A组:2,3.
B组:1.
