3.3几何概型
图片预览









文档简介
(共46张PPT)
3.3 几何概型
3.3.1 几何概型
3.3.2 均匀随机数的产生
3.3 几何概型
3.3.1 几何概型
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件出现的可能性相等(等可能性).
1、古典概型有哪两个基本特点?
复习
2、计算随机事件发生的概率,我们已经学习了哪些方法
(2)通过做试验或计算机模拟试验,用频率来近似估计概率;
(1)利用古典概型的概率公式计算.
3、在现实生活中,常常会遇到试验的所有可能结果是无穷多的情况,这时就不能用古典概型来计算事件发生的概率.
例如:一个人到单位的时间可能是8:00~9:00之间的任何一个时刻;往一个方格中投一个石子,石子可能落在方格中的任何一点上……这两个试验可能出现的结果是有限个,还是无限个?若没有人为因素,每个试验结果出现的可能性是否相等?
特定情形下,我们可以用几何概型来计算事件发生的概率.
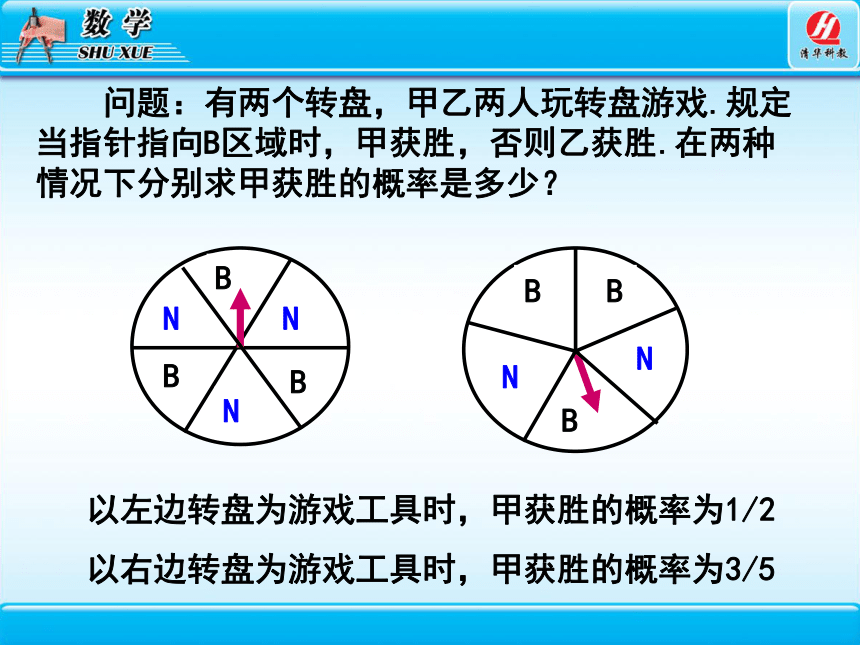
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
以左边转盘为游戏工具时,甲获胜的概率为1/2
以右边转盘为游戏工具时,甲获胜的概率为3/5
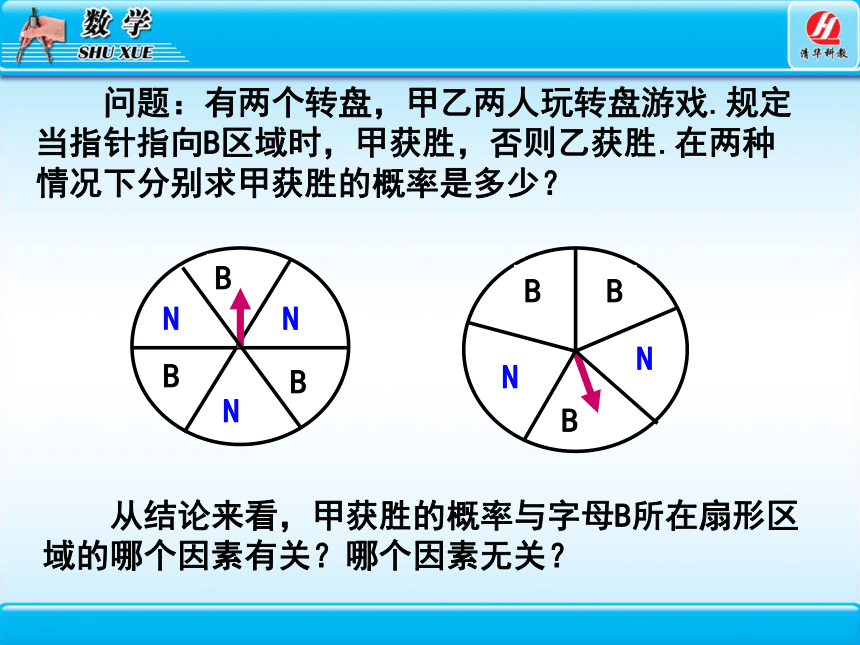
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
从结论来看,甲获胜的概率与字母B所在扇形区域的哪个因素有关?哪个因素无关?
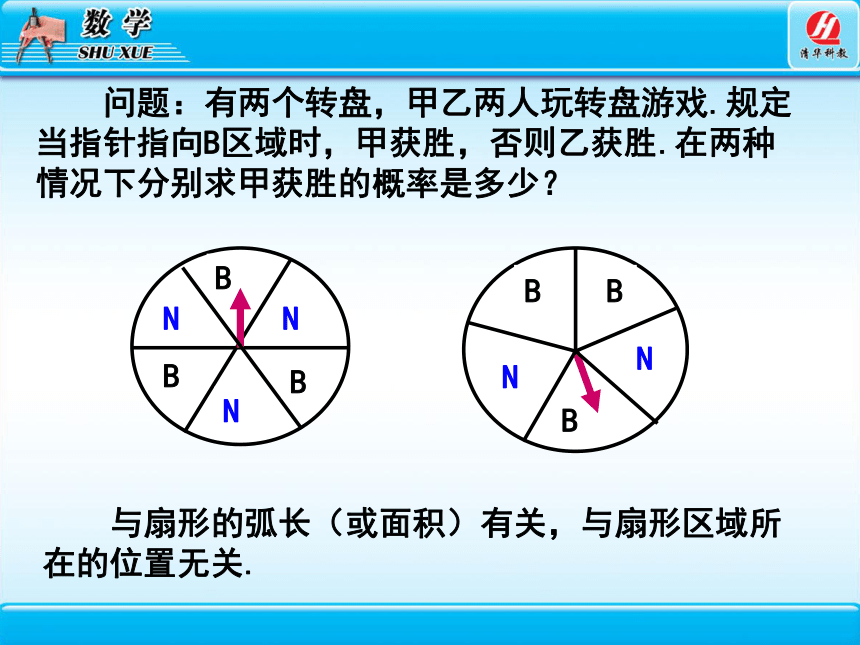
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
与扇形的弧长(或面积)有关,与扇形区域所在的位置无关.
几何概率模型的定义
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
几何概型的特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个.
(2)每个基本事件出现的可能性相等.
练习1:某班公交车到终点站的时间等可能是11:30~12:00之间的任何一个时刻,那么“公交车在11:40~11:50到终点站”这个随机事件是几何概型吗?若是,怎样理解其几何意义?
练习2:一个游戏转盘如图,让转盘自由转动,当转盘停止转动后,指针落在哪个区域.这个随机事件是几何概型吗?为什么?落在哪个区域的可能性最大 落在哪个区域的可能性最小 有可能性相等的情况吗 为什么
60
90
90
120
解:是几何概型,因为事件发生的概率只与构成该事件区域的面积成比例,
练习2:一个游戏转盘如图,让转盘自由转动,当转盘停止转动后,指针落在哪个区域这个随机事件是几何概型吗?为什么?落在哪个区域的可能性最大 落在哪个区域的可能性最小 有可能性相等的情况吗 为什么
60
90
90
120
解:落在红色区域可能性最大,落在蓝色区域可能性最小,黄色和绿色可能性相同,
这是几何概型,可以通过图形的面积判断.
对于具有几何意义的随机事件,或可以化归为几何问题的随机事件,一般都有几何概型的特性,我们希望建立一个求几何概型的概率公式.
60
90
90
120
在刚才的转盘游戏中,落在各颜色区域的概率各是多少?
在几何概型中,事件A的概率的计算公式如下:
解:设A={等待的时间不多于10分钟}.我们所
关心的事件A恰好是打开收音机的时刻位于
[50,60]时间段内,因此由几何概型的求概率
的公式得
例1:某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
即“等待的时间不超过10分钟”的概率为
练习:某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大 遇到哪一种灯的可能性最小 根据什么
遇到红灯,绿灯,黄灯的概率各是多少?为什么?
例2:甲乙两人相约上午8点到9点在某地会面,先到者等候另一人20分钟,过时离去,求甲乙两人能会面的概率.
O
x
y
20
20
60
60
练习:甲乙两人相约下午1时至2时在某公共汽车站乘车,已知该站在下午1时30分和2时准点各发一班车,假设因堵车的影响,甲乙两人在1时至2时之间任一时刻到达车站的可能性相同,如果两人到车站后见车就上,那么两人乘一辆车的概率是多少?
例3:如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成了2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏,规定小夏转甲盘一次,小秋转乙盘一次为一次游戏(当指针指在边界线上视为无效,重转) 小夏说:“如果两个指针所指的区域内的数之和是6或7,则我胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
甲盘
乙盘
小结
1、几何概率模型的定义
2、几何概型的特点
3、在几何概型中,事件A的概率的计算公式:
4、如果一个随机试验可能出现的结果有无限多个,并且每个结果发生的可能性相等,那么该试验可以看作是几何概型.通过适当设置,将随机事件转化为几何问题,即可利用几何概型的概率公式求事件发生的概率.
布置作业:
P140 练习: 1,2.
P142 习题3.3A组:1.
3.3.2 均匀随机数的产生
复习
1、几何概型的含义是什么?它有哪两个基本特点?
含义:每个事件发生的概率只与构成该事件区域的的长度(面积或体积)成比例的概率模型.
特点:(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
2、在几何概型中,事件A的概率的计算公式:
我们常用的是[0,1]上的均匀随机数,可以利用计算器来产生.如何利用计算器产生0~1之间的均匀随机数(实数)?
PRB
ENTER
ENTER
RAND RANDI
STAT DEG
RANDI
0.052745889
STAT DEG
注意:每次结果会有不同.
(2)选定Al格,点击复制,然后选定要产生随机数的格,比如A2~A100,点击粘贴,则在A1~A100的数都是[0,1]上的均匀随机数.这样我们就很快就得到了100个0~1之间的均匀随机数,相当于做了100次随机试验.
(1)选定Al格,键人“=RAND()”,按Enter键,则在此格中的数是随机产生的[0,1]上的均匀随机数;
用Excel演示.
试验的结果是区间[0,1]上的任何一个实数,而且出现任何一个实数是等可能的,因此,就可以用上面的方法产生的0~1之间的均匀随机数进行随机模拟.
我们可以利用计算器或计算机产生整数值随机数,还可以通过随机模拟方法求古典概型的概率近似值,对于几何概型,我们也可以进行上述工作.
思考:计算机只能产生[0,1]上的均匀随机数,如果试验的结果是区间[a,b]上等可能出现的任何一个值,如何产生[a,b]上的均匀随机数?
首先利用计算器或计算机产生[0,1]上的均匀随机数X=RAND, 然后利用伸缩和平移变换:
计算Y的值,则Y为[a,b]上的均匀随机数.
练习:怎样利用计算机产生100个[2,5]上的均匀随机数?
(1)在A1~A100产生100个0~1之间的均匀随机数;
(2)选定Bl格,键人“=A1*3+2”,按Enter键,则在此格中的数是随机产生的[2,5]上的均匀随机数;
(3)选定Bl格,拖动至B100,则在B1~B100的数都是[2,5]上的均匀随机数.
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
随机事件
1、如果把“父亲在离开家之前能得到报纸”称为事件A,那么事件A是哪种类型的事件?
分析:
2、我们有两种方法计算该事件的概率:
⑴利用几何概型的公式;
⑵用随机模拟的方法.
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
⑴利用几何概型的公式;
设送报人到达你家的时间为x,父亲离开家的时间为y,若事件A发生,则x、y应满足什么关系?
6.5≤x≤7.5,7≤y≤8,y≥x.
你能画出上述不等式组表示的平面区域吗?
根据几何概型的概率计算公式,事件A发生的概率为多少?
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
试验的全部结果所构成的区域为
={(x,y)| 6.5≤x≤7.5,7≤y≤8 },这是一个正方形区域,面积为1.
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
事件A表示父亲在离开家前能得到报纸,所构成的区域A={(x,y)| 6.5≤x≤7.5,7≤y≤8, y≥x },
即图中的阴影部分,面积为
这是一个几何概型,所以
思考:你能设计一种随机模拟的方法,近似计算上面事件A发生的概率吗?
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
⑵用随机模拟的方法.
设X、Y为[0,1]上的均匀随机数,6.5+X表示送报人到达你家的时间,7+Y表示父亲离开家的时间,若父亲在离开家之前能得到报纸,则X、Y应满足:
7+Y >6.5+X,即Y>X-0.5.
(2)选定D1格,键入“=A1-B1”,按Enter键. 再选定Dl格,拖动至D50,则在D1~D50的数为Y-X的值;
(3)选定E1格,键入
“=FREQUENCY(D1:D50,-0.5)”,
统计D列中小于-0.5的数的频数;
利用计算机做50次模拟试验,计算事件A发生的频率,从而估计事件A发生的概率.
(1)在A1~A50,B1~B50产生两组[0,1]上的均匀随机数;
例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.
(1)圆面积︰正方形面积
≈落在圆中的豆子数︰落在正方形中的豆子数.
(2)设正方形的边长为2,则
圆面积︰正方形面积= /(2×2)= /4.
(3)由于落在每个区域的豆子数是可以数出来的,所以 ≈落在圆中的豆子数︰落在正方形中的豆子数×4.
这样就得到了 的近似值.
例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.
另外,我们可以用计算器或计算机模拟上述过程,步骤如下:
⑴产生两组0-1之间的均匀随机数,a1=RAND,b1=RAND;
⑵经平移和伸缩变换,a=2(a1﹣0.5),
b=2(b1﹣0.5);
⑶数出落在圆内x2+y2<1的点(a,b)的个数N1,计算 =4N1/N(N代表落在正方形中的点(a,b)的个数).
可以发现,随着试验次数的增加,得到的 的近似值的精度会越来越高.
本例启发我们,利用几何概型,并通过随机模拟方法可以近似计算不规则图形的面积.
例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.
x
y
0
1
-1
1
以直线x=1,x=-1,y=0,y=1为边界作矩形,
用随机模拟方法可以得到它的面积的近似值.
例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.
x
y
0
1
-1
1
解:⑴产生两组0-1区间的均匀随机数,a1=RAND,b=RAND;
⑵进行平移和伸缩变换,a=2(a1﹣0.5);
⑶数出落在阴影内的样本点数N1,用几何概型公式计算阴影部分的面积.
小结
1、利用计算机和线性变换Y=X× (b-a)+a,可以产生任意区间[a,b]上的均匀随机数.
2、利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值.
3、均匀随机数在日常生活中,有着广泛的应用,我们可以利用计算器或计算机来产生均匀随机数,从而来模拟随机试验,其具体方法是:建立一个概率模型,它与某些我们感兴趣的量(如概率值、常数)有关,然后设计适当的试验,并通过这个试验的结果来确定这些量 .
布置作业:
P142 习题3.3A组:2,3.
B组:1,2
3.3 几何概型
3.3.1 几何概型
3.3.2 均匀随机数的产生
3.3 几何概型
3.3.1 几何概型
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件出现的可能性相等(等可能性).
1、古典概型有哪两个基本特点?
复习
2、计算随机事件发生的概率,我们已经学习了哪些方法
(2)通过做试验或计算机模拟试验,用频率来近似估计概率;
(1)利用古典概型的概率公式计算.
3、在现实生活中,常常会遇到试验的所有可能结果是无穷多的情况,这时就不能用古典概型来计算事件发生的概率.
例如:一个人到单位的时间可能是8:00~9:00之间的任何一个时刻;往一个方格中投一个石子,石子可能落在方格中的任何一点上……这两个试验可能出现的结果是有限个,还是无限个?若没有人为因素,每个试验结果出现的可能性是否相等?
特定情形下,我们可以用几何概型来计算事件发生的概率.
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
以左边转盘为游戏工具时,甲获胜的概率为1/2
以右边转盘为游戏工具时,甲获胜的概率为3/5
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
从结论来看,甲获胜的概率与字母B所在扇形区域的哪个因素有关?哪个因素无关?
问题:有两个转盘,甲乙两人玩转盘游戏.规定当指针指向B区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?
B
N
B
B
N
N
B
B
B
N
N
与扇形的弧长(或面积)有关,与扇形区域所在的位置无关.
几何概率模型的定义
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
几何概型的特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个.
(2)每个基本事件出现的可能性相等.
练习1:某班公交车到终点站的时间等可能是11:30~12:00之间的任何一个时刻,那么“公交车在11:40~11:50到终点站”这个随机事件是几何概型吗?若是,怎样理解其几何意义?
练习2:一个游戏转盘如图,让转盘自由转动,当转盘停止转动后,指针落在哪个区域.这个随机事件是几何概型吗?为什么?落在哪个区域的可能性最大 落在哪个区域的可能性最小 有可能性相等的情况吗 为什么
60
90
90
120
解:是几何概型,因为事件发生的概率只与构成该事件区域的面积成比例,
练习2:一个游戏转盘如图,让转盘自由转动,当转盘停止转动后,指针落在哪个区域这个随机事件是几何概型吗?为什么?落在哪个区域的可能性最大 落在哪个区域的可能性最小 有可能性相等的情况吗 为什么
60
90
90
120
解:落在红色区域可能性最大,落在蓝色区域可能性最小,黄色和绿色可能性相同,
这是几何概型,可以通过图形的面积判断.
对于具有几何意义的随机事件,或可以化归为几何问题的随机事件,一般都有几何概型的特性,我们希望建立一个求几何概型的概率公式.
60
90
90
120
在刚才的转盘游戏中,落在各颜色区域的概率各是多少?
在几何概型中,事件A的概率的计算公式如下:
解:设A={等待的时间不多于10分钟}.我们所
关心的事件A恰好是打开收音机的时刻位于
[50,60]时间段内,因此由几何概型的求概率
的公式得
例1:某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
即“等待的时间不超过10分钟”的概率为
练习:某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大 遇到哪一种灯的可能性最小 根据什么
遇到红灯,绿灯,黄灯的概率各是多少?为什么?
例2:甲乙两人相约上午8点到9点在某地会面,先到者等候另一人20分钟,过时离去,求甲乙两人能会面的概率.
O
x
y
20
20
60
60
练习:甲乙两人相约下午1时至2时在某公共汽车站乘车,已知该站在下午1时30分和2时准点各发一班车,假设因堵车的影响,甲乙两人在1时至2时之间任一时刻到达车站的可能性相同,如果两人到车站后见车就上,那么两人乘一辆车的概率是多少?
例3:如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成了2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏,规定小夏转甲盘一次,小秋转乙盘一次为一次游戏(当指针指在边界线上视为无效,重转) 小夏说:“如果两个指针所指的区域内的数之和是6或7,则我胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
甲盘
乙盘
小结
1、几何概率模型的定义
2、几何概型的特点
3、在几何概型中,事件A的概率的计算公式:
4、如果一个随机试验可能出现的结果有无限多个,并且每个结果发生的可能性相等,那么该试验可以看作是几何概型.通过适当设置,将随机事件转化为几何问题,即可利用几何概型的概率公式求事件发生的概率.
布置作业:
P140 练习: 1,2.
P142 习题3.3A组:1.
3.3.2 均匀随机数的产生
复习
1、几何概型的含义是什么?它有哪两个基本特点?
含义:每个事件发生的概率只与构成该事件区域的的长度(面积或体积)成比例的概率模型.
特点:(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
2、在几何概型中,事件A的概率的计算公式:
我们常用的是[0,1]上的均匀随机数,可以利用计算器来产生.如何利用计算器产生0~1之间的均匀随机数(实数)?
PRB
ENTER
ENTER
RAND RANDI
STAT DEG
RANDI
0.052745889
STAT DEG
注意:每次结果会有不同.
(2)选定Al格,点击复制,然后选定要产生随机数的格,比如A2~A100,点击粘贴,则在A1~A100的数都是[0,1]上的均匀随机数.这样我们就很快就得到了100个0~1之间的均匀随机数,相当于做了100次随机试验.
(1)选定Al格,键人“=RAND()”,按Enter键,则在此格中的数是随机产生的[0,1]上的均匀随机数;
用Excel演示.
试验的结果是区间[0,1]上的任何一个实数,而且出现任何一个实数是等可能的,因此,就可以用上面的方法产生的0~1之间的均匀随机数进行随机模拟.
我们可以利用计算器或计算机产生整数值随机数,还可以通过随机模拟方法求古典概型的概率近似值,对于几何概型,我们也可以进行上述工作.
思考:计算机只能产生[0,1]上的均匀随机数,如果试验的结果是区间[a,b]上等可能出现的任何一个值,如何产生[a,b]上的均匀随机数?
首先利用计算器或计算机产生[0,1]上的均匀随机数X=RAND, 然后利用伸缩和平移变换:
计算Y的值,则Y为[a,b]上的均匀随机数.
练习:怎样利用计算机产生100个[2,5]上的均匀随机数?
(1)在A1~A100产生100个0~1之间的均匀随机数;
(2)选定Bl格,键人“=A1*3+2”,按Enter键,则在此格中的数是随机产生的[2,5]上的均匀随机数;
(3)选定Bl格,拖动至B100,则在B1~B100的数都是[2,5]上的均匀随机数.
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
随机事件
1、如果把“父亲在离开家之前能得到报纸”称为事件A,那么事件A是哪种类型的事件?
分析:
2、我们有两种方法计算该事件的概率:
⑴利用几何概型的公式;
⑵用随机模拟的方法.
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
⑴利用几何概型的公式;
设送报人到达你家的时间为x,父亲离开家的时间为y,若事件A发生,则x、y应满足什么关系?
6.5≤x≤7.5,7≤y≤8,y≥x.
你能画出上述不等式组表示的平面区域吗?
根据几何概型的概率计算公式,事件A发生的概率为多少?
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
试验的全部结果所构成的区域为
={(x,y)| 6.5≤x≤7.5,7≤y≤8 },这是一个正方形区域,面积为1.
y
6.5
7.5
x
O
7
8
6.5≤x≤7.5,7≤y≤8,y≥x.
事件A表示父亲在离开家前能得到报纸,所构成的区域A={(x,y)| 6.5≤x≤7.5,7≤y≤8, y≥x },
即图中的阴影部分,面积为
这是一个几何概型,所以
思考:你能设计一种随机模拟的方法,近似计算上面事件A发生的概率吗?
例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?
⑵用随机模拟的方法.
设X、Y为[0,1]上的均匀随机数,6.5+X表示送报人到达你家的时间,7+Y表示父亲离开家的时间,若父亲在离开家之前能得到报纸,则X、Y应满足:
7+Y >6.5+X,即Y>X-0.5.
(2)选定D1格,键入“=A1-B1”,按Enter键. 再选定Dl格,拖动至D50,则在D1~D50的数为Y-X的值;
(3)选定E1格,键入
“=FREQUENCY(D1:D50,-0.5)”,
统计D列中小于-0.5的数的频数;
利用计算机做50次模拟试验,计算事件A发生的频率,从而估计事件A发生的概率.
(1)在A1~A50,B1~B50产生两组[0,1]上的均匀随机数;
例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.
(1)圆面积︰正方形面积
≈落在圆中的豆子数︰落在正方形中的豆子数.
(2)设正方形的边长为2,则
圆面积︰正方形面积= /(2×2)= /4.
(3)由于落在每个区域的豆子数是可以数出来的,所以 ≈落在圆中的豆子数︰落在正方形中的豆子数×4.
这样就得到了 的近似值.
例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.
另外,我们可以用计算器或计算机模拟上述过程,步骤如下:
⑴产生两组0-1之间的均匀随机数,a1=RAND,b1=RAND;
⑵经平移和伸缩变换,a=2(a1﹣0.5),
b=2(b1﹣0.5);
⑶数出落在圆内x2+y2<1的点(a,b)的个数N1,计算 =4N1/N(N代表落在正方形中的点(a,b)的个数).
可以发现,随着试验次数的增加,得到的 的近似值的精度会越来越高.
本例启发我们,利用几何概型,并通过随机模拟方法可以近似计算不规则图形的面积.
例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.
x
y
0
1
-1
1
以直线x=1,x=-1,y=0,y=1为边界作矩形,
用随机模拟方法可以得到它的面积的近似值.
例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.
x
y
0
1
-1
1
解:⑴产生两组0-1区间的均匀随机数,a1=RAND,b=RAND;
⑵进行平移和伸缩变换,a=2(a1﹣0.5);
⑶数出落在阴影内的样本点数N1,用几何概型公式计算阴影部分的面积.
小结
1、利用计算机和线性变换Y=X× (b-a)+a,可以产生任意区间[a,b]上的均匀随机数.
2、利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值.
3、均匀随机数在日常生活中,有着广泛的应用,我们可以利用计算器或计算机来产生均匀随机数,从而来模拟随机试验,其具体方法是:建立一个概率模型,它与某些我们感兴趣的量(如概率值、常数)有关,然后设计适当的试验,并通过这个试验的结果来确定这些量 .
布置作业:
P142 习题3.3A组:2,3.
B组:1,2
