2021-2022学年人教版八年级数学上册 13.1.1轴对称图形 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册 13.1.1轴对称图形 课件(共21张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
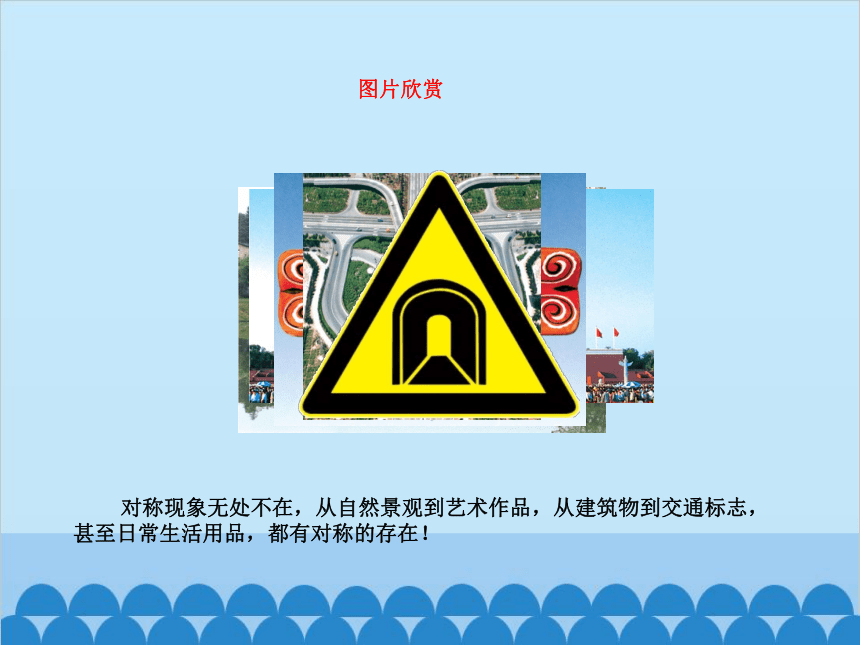
图片欣赏
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标志,甚至日常生活用品,都有对称的存在!
13.1.1
轴对称
复习巩固
我们研究几何图形的三个步骤是什么?
定义、性质、判定
学习目标:理解轴对称图形和两个图形关于某直线对称、线段垂直平分线的相关概念,理解和掌握轴对称的性质.
学习目标
自学
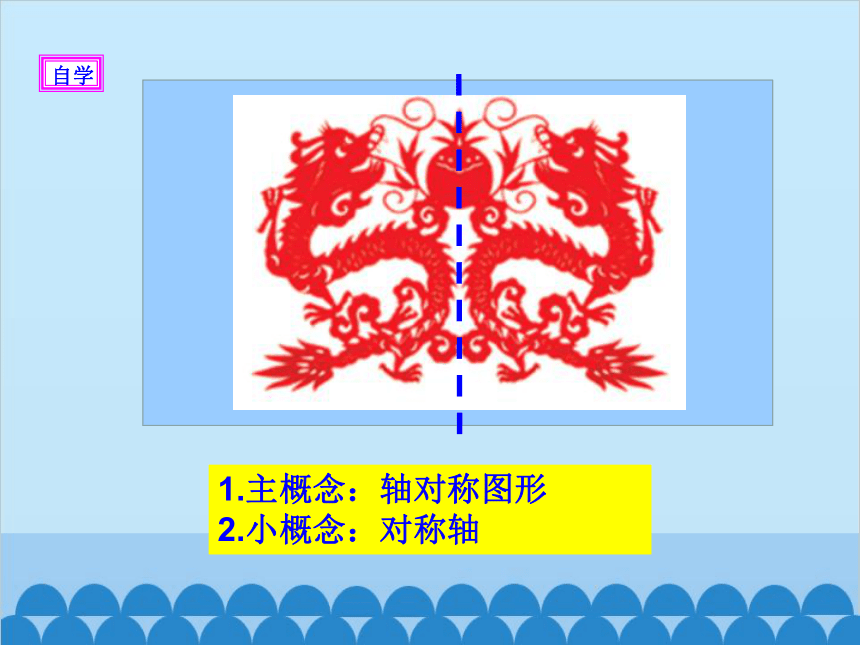
1.主概念:轴对称图形
2.小概念:对称轴
自学
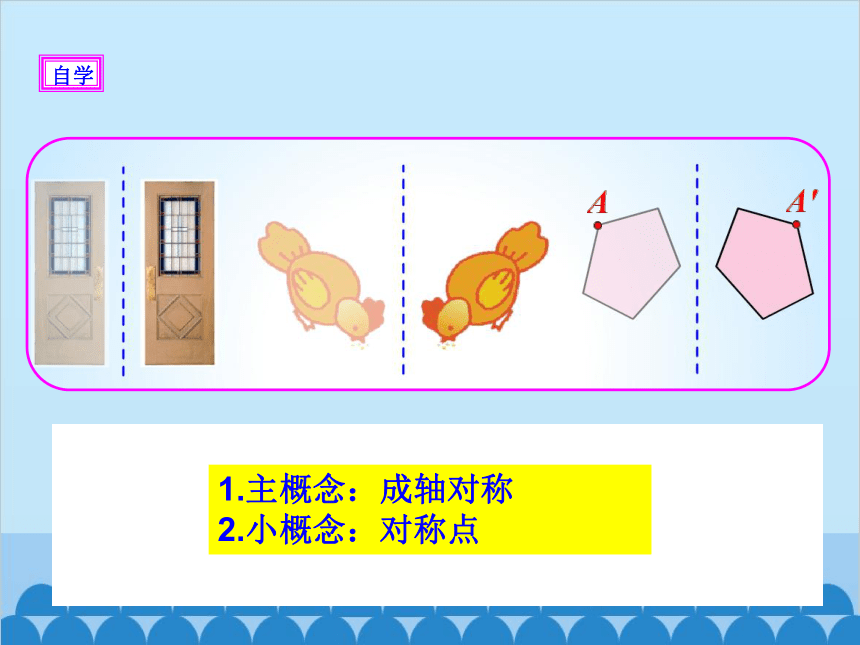
每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
1.主概念:成轴对称
2.小概念:对称点
轴对称图形
两个图形成轴对称
区别
_____个图形
____个图形
联系
1.沿一条直线折叠,直线两旁的部分能够
_________.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个
图形,那么这两个图形关于这条直线___;
如果把两个成轴对称的图形看成一个图形,那
么这个图形就是______________.
一
两
互相重合
对称轴
成轴对称
轴对称图形
总结
思考
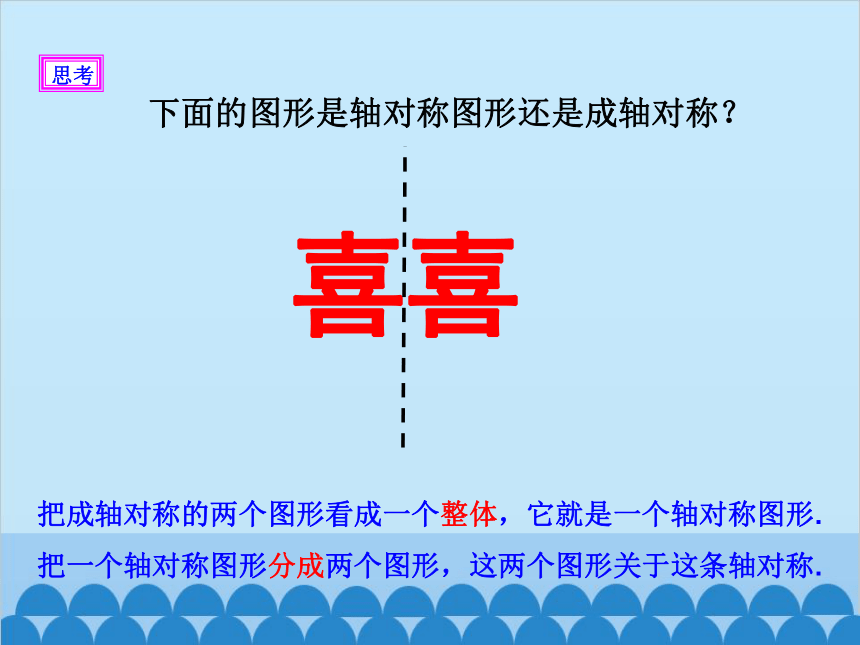
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形分成两个图形,这两个图形关于这条轴对称.
喜喜
下面的图形是轴对称图形还是成轴对称?
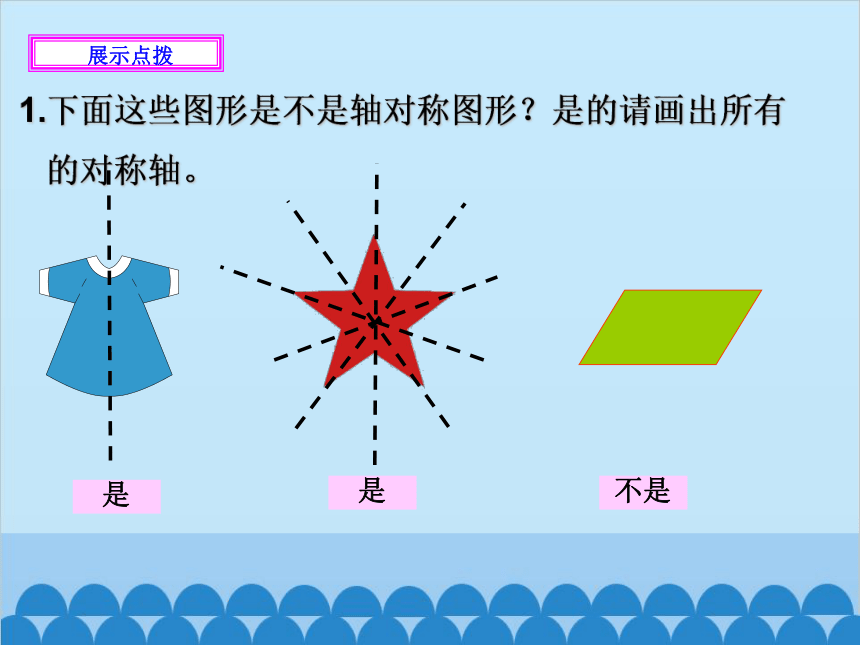
1.下面这些图形是不是轴对称图形?是的请画出所有
的对称轴。
是
是
不是
展示点拨
2.圆是不是轴对称图形?它的对称轴是直径吗?
圆有多少条对称轴?
展示点拨
展示点拨
3.如图,△ABC与△A′B′C′关于直线l对称,则∠B的度数为(
)
A.30°
B.50°
C.90°
D.100°
D
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
P
总结
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
成轴对称的两个图形的性质:
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
轴对称图形的性质:
展示点拨
4.
如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出图中相等的线段;
(3)图中还有对称的三角形吗?
(4)画出并写出图中被直线MN所垂直平分的线段。
解:(1)B和D,C和E,A和A,F和F
(2)AC=AE,AB=AD,BC=DE,
BF=DF,CF=EF
(3)有,△AFB和△AFD,△AEF和△ACF
(4)线段EC、线段BD
今天我们学习了哪些知识?
谈收获
当堂达标
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是(
)
A
当堂达标
2.下列轴对称图形中,对称轴只有两条的是(
)
C
3.一辆汽车的牌照在路面旁水面的倒影为
则该车的牌照号码为
.
M12569
当堂达标
当堂达标
4.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知
AC=5
cm,△ADC的周长为17
cm,则BC的长为( )
A.7
cm
B.10
cm
C.12
cm
D.22
cm
C
拓展提高
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
证明:(1)∵∠GCF+∠FCE=90°,
∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
在△FGC与△EBC中,
∴△FGC≌△EBC(AAS)
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:
(2)由折叠知
S四边形ECGF=S四边形EADF
∵△FGC≌△EBC
∴S△FGC=S△EBC
∴S△FGC+S△EFC=S△EFC+S△EBC
∴S四边形ECGF=S四边形EBCF
∴S四边形EADF=S四边形EBCF=
S长方形=
×8×4=16
∴S四边形ECGF=16
拓展提高
图片欣赏
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标志,甚至日常生活用品,都有对称的存在!
13.1.1
轴对称
复习巩固
我们研究几何图形的三个步骤是什么?
定义、性质、判定
学习目标:理解轴对称图形和两个图形关于某直线对称、线段垂直平分线的相关概念,理解和掌握轴对称的性质.
学习目标
自学
1.主概念:轴对称图形
2.小概念:对称轴
自学
每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
1.主概念:成轴对称
2.小概念:对称点
轴对称图形
两个图形成轴对称
区别
_____个图形
____个图形
联系
1.沿一条直线折叠,直线两旁的部分能够
_________.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个
图形,那么这两个图形关于这条直线___;
如果把两个成轴对称的图形看成一个图形,那
么这个图形就是______________.
一
两
互相重合
对称轴
成轴对称
轴对称图形
总结
思考
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形分成两个图形,这两个图形关于这条轴对称.
喜喜
下面的图形是轴对称图形还是成轴对称?
1.下面这些图形是不是轴对称图形?是的请画出所有
的对称轴。
是
是
不是
展示点拨
2.圆是不是轴对称图形?它的对称轴是直径吗?
圆有多少条对称轴?
展示点拨
展示点拨
3.如图,△ABC与△A′B′C′关于直线l对称,则∠B的度数为(
)
A.30°
B.50°
C.90°
D.100°
D
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
P
总结
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
成轴对称的两个图形的性质:
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
轴对称图形的性质:
展示点拨
4.
如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出图中相等的线段;
(3)图中还有对称的三角形吗?
(4)画出并写出图中被直线MN所垂直平分的线段。
解:(1)B和D,C和E,A和A,F和F
(2)AC=AE,AB=AD,BC=DE,
BF=DF,CF=EF
(3)有,△AFB和△AFD,△AEF和△ACF
(4)线段EC、线段BD
今天我们学习了哪些知识?
谈收获
当堂达标
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是(
)
A
当堂达标
2.下列轴对称图形中,对称轴只有两条的是(
)
C
3.一辆汽车的牌照在路面旁水面的倒影为
则该车的牌照号码为
.
M12569
当堂达标
当堂达标
4.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知
AC=5
cm,△ADC的周长为17
cm,则BC的长为( )
A.7
cm
B.10
cm
C.12
cm
D.22
cm
C
拓展提高
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
证明:(1)∵∠GCF+∠FCE=90°,
∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
在△FGC与△EBC中,
∴△FGC≌△EBC(AAS)
如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:
(2)由折叠知
S四边形ECGF=S四边形EADF
∵△FGC≌△EBC
∴S△FGC=S△EBC
∴S△FGC+S△EFC=S△EFC+S△EBC
∴S四边形ECGF=S四边形EBCF
∴S四边形EADF=S四边形EBCF=
S长方形=
×8×4=16
∴S四边形ECGF=16
拓展提高
