2020-2021学年冀教新版九年级上册数学《第23章 数据分析》单元测试卷(word版有答案)
文档属性
| 名称 | 2020-2021学年冀教新版九年级上册数学《第23章 数据分析》单元测试卷(word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 11:17:55 | ||
图片预览




文档简介
2020-2021学年冀教新版九年级上册数学《第23章
数据分析》单元测试卷
一.选择题
1.某学校初、高六个年级共有2000名学生,为了了解其视力情况,现采用抽样调查,如果按10%的比例抽样,则样本容量是( )
A.2000
B.10
C.200
D.10%
2.某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=3:2的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是( )
A.43分
B.85分
C.86分
D.170分
3.某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5
B.6
C.0.5
D.﹣6
4.下列问题中,应采用抽样调查的是( )
A.企业招聘,对应聘人员进行面试
B.了解某班学生的身高情况
C.调查春节联欢晚会的收视率
D.了解某校七年级第二学期期末考试各班的数学科平均成绩
5.小明在计算一组数据的方差时,列出的公式如下:s2=,根据公式信息,下列说法中,错误的是( )
A.数据个数是5
B.数据平均数是8
C.数据众数是8
D.数据方差是0
6.为全力抗战疫情,响应政府“停课不停学”号召,东营市教育局发布关于疫情防控期间开展在线课程教学的通知:从2月10日开始,全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2月10日在线答疑问题总个数如下表所示,则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
学科
语文
数学
英语
物理
化学
道法
历史
数量/个
26
28
28
26
24
21
22
A.22
B.24
C.25
D.26
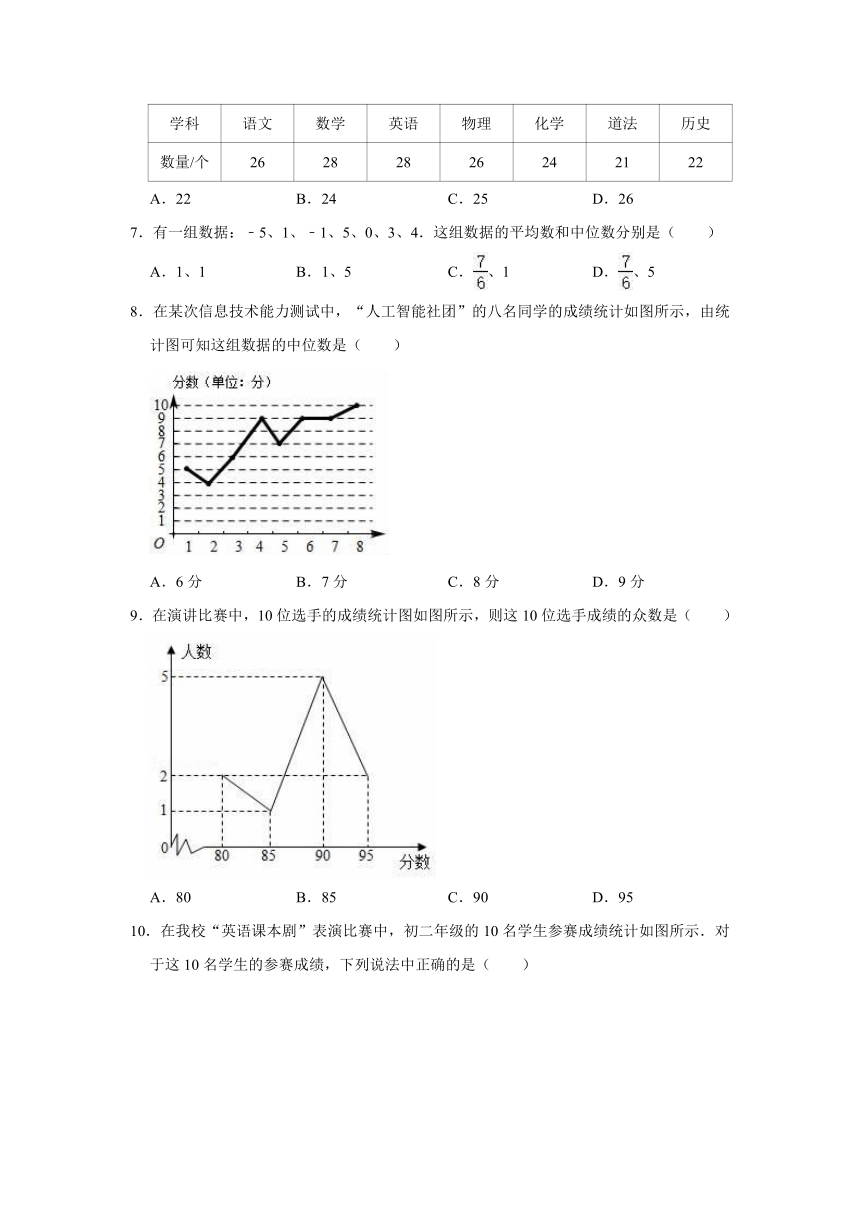
7.有一组数据:﹣5、1、﹣1、5、0、3、4.这组数据的平均数和中位数分别是( )
A.1、1
B.1、5
C.、1
D.、5
8.在某次信息技术能力测试中,“人工智能社团”的八名同学的成绩统计如图所示,由统计图可知这组数据的中位数是( )
A.6分
B.7分
C.8分
D.9分
9.在演讲比赛中,10位选手的成绩统计图如图所示,则这10位选手成绩的众数是( )
A.80
B.85
C.90
D.95
10.在我校“英语课本剧”表演比赛中,初二年级的10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中正确的是( )
A.众数是90
B.平均数是88
C.中位数是85
D.方差是6
二.填空题
11.从一批洗衣机中抽取10台,调查这批洗衣机的使用寿命,在这一抽样调查中,样本容量是
.
12.一组数据2,1,3,1,2,4的中位数是
.
13.已知一组数据1,4,a,3,5,若它的平均数是3,则这组数据的中位数是
.
14.学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如表,请你根据表中的数据选一人参加比赛,最适合的人选是
.(填甲、乙中的一个)
选手
甲
乙
平均数(环)
9.5
9.5
方差
0.035
0.015
15.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是S甲2=36,S乙2=30,则两组成绩的比较稳定的是
.
16.已知一组数据2、a、6、9、12的平均数为7,则a=
.
17.已知一组数据x1、x2、x3、x4的平均数是3,则数据x1﹣1、x2﹣1、x3﹣1、x4﹣1的平均数是
.
18.某次射击训练中,一小组的成绩如下表所示:
环数
7
8
9
人数
3
4
已知该小组的平均成绩为8环,那么成绩为9环的人数是
.
19.数据2,7,5,7,9的众数、中位数、平均数分别是
、
、
.
20.小颖使用计算器求30个数据的平均数时,错将其中一个数据15输入为105,那么由此求出的平均数与实际平均数的差是
.
三.解答题
21.某校八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,指出下列说法中哪些是正确的.
(1)这种调查方式是抽样调查.
(2)800名学生是总体.
(3)每名学生的立定跳远成绩是个体.
(4)这100名学生的立定跳远成绩是总体的一个样本.
(5)100名学生是样本容量.
22.为宣传6月8日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
表1:知识竞赛成绩分组统计表
组别
分数/分
频数
A
60≤x<70
a
B
70≤x<80
20
C
80≤x<90
28
D
90≤x<100
36
(1)本次调查一共随机抽取了
个参赛学生的成绩;
(2)表1中a=
;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是
;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有
人.
23.某养猪场要出售200只生猪,现在市场上生猪的价格为11元/kg,为了估计这200只生猪能卖多少钱,该养猪场从中随机抽取5只,每只猪的重量(单位:kg)如下:76,71,72,86,87.
(1)计算这5只生猪的平均重量;
(2)估计这200只生猪能卖多少钱?
24.某公司有500名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:
①将过去的自主选餐改为提供统一的套餐;
②调查了全体职员复工后的午餐意向,结果如图所示;
③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳160人用餐;
④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;
⑤随机邀请了100名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这100名职员取餐共用时10min,用餐时间(含用餐与回收餐具)如表所示.
为节约时间,食堂决定将第一排用餐职员160人的套餐先摆放在相应餐桌上,并在12:00开始用餐,其他职员则需自行取餐.
用餐时间x/min
人数
15<x≤17
20
17<x≤19
40
19<x≤21
18
21<x≤23
14
23<x≤25
8
(1)食堂每天需要准备多少份午餐?
(2)食堂打算以参加演练的100名职员用餐时间的平均数min为依据进行规划:前一批职员用餐min后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过13:00就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
25.某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图.请根据相关信息,解答下列问题:
(1)求统计的这组数据的平均数、中位数;
(2)根据样本数据,估计这2500只鸡中,质量为2.0kg的约有多少只?
26.下列各数是10名学生在某一次数学考试中的成绩:92,93,88,76,100,90,71,97,92,91
(1)他们的最高分与最低分的差是
;
(2)请先用一个整十的数估计他们的平均成绩是
,把每一名学生的成绩都减去平均成绩的估计值,得到一组新数据,计算出新数据的平均成绩,然后在此基础上计算原成绩的平均成绩,由此检验你的估算能力.
参考答案与试题解析
一.选择题
1.解:2000×10%=200,
故样本容量是200.
故选:C.
2.解:∵(90×3+80×2)÷(3+2)
=430÷5
=86(分)
∴该竞聘教师的最后成绩是86分.
故选:C.
3.解:求15个数据的平均数时,错将其中一个数据15输入为105,即使总和增加了90;那么由此求出的这组数据的平均数与实际平均数的差是90÷15=6.
故选:B.
4.解:A、企业招聘,对应聘人员进行面试应采用全面调查;
B、了解某班学生的身高情况应采用全面调查;
C、调查春节联欢晚会的收视率应采用抽样调查;
D、了解某校七年级第二学期期末考试各班的数学科平均成绩应采用全面调查;
故选:C.
5.解:∵s2=,
∴样本容量是5,故选项A正确,
样本平均数是:=8,故选项B正确,
样本众数是8,故选项C正确,
样本方差是:s2=
[(7﹣8)2+(8﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]=,故选项D错误,
故选:D.
6.解:(26+28+28+26+24+21+22)÷7
=175÷7
=25.
故选:C.
7.解:平均数=(﹣5+1﹣1+5+0+3+4)÷7=1;
把这组数据按从大到小的顺序排列是:﹣5,﹣1,0,1,3,4,5,
故这组数据的中位数是1.
故选:A.
8.解:把这组数据由小到大排列,得4,5,6,7,9,9,9,10,
最中间的两个数是7,9,
所以这组数据的中位数是(7+9)÷2=8(分).
故选:C.
9.解:由题意得:90分出现的次数最多,
∴这10位选手成绩的众数是90(分),
故选:C.
10.解:∵90出现了5次,出现的次数最多,
∴众数是90;
故A正确;
∵平均数是(80×1+85×2+90×5+95×2)÷10=89;
故B错误;
共有10个数,
∴中位数是第5、6个数的平均数,
∴中位数是(90+90)÷2=90;
故C错误;
方差为×[(89﹣80)2+2×(89﹣85)2+2×(89﹣95)2+(89﹣90)2×5]=19,
故D错误.
故选:A.
二.填空题
11.解:从一批洗衣机中抽取10台,调查这批洗衣机的使用寿命,在这一抽样调查中,样本容量是10.
故答案为:10.
12.解:将这组数据从小到大的顺序排列:1,1,2,2,3,4,处于中间位置的两个数是2,2,那么由中位数的定义可知,这组数据的中位数是(2+2)÷2=2.
故答案为:2.
13.解:由题意得(1+4+a+3+5)=3,
解得:a=2,
这组数据按照从小到大的顺序排列为:1,2,3,4,5,
则中位数为3.
故答案为:3.
14.解:因为S甲2=0.035>S乙2=0.015,方差小的为乙,
所以本题中成绩比较稳定的是乙.
所以最适合的人选是乙.
故答案为乙.
15.解:∵S甲2>S乙2,
∴乙的成绩比较稳定,
故答案为:乙.
16.解:由题意知,平均数=(2+a+6+9+12)÷5=7,
所以a=5×7﹣(2+6+9+12)=6.
故答案为:6.
17.解:∵x1,x2,x3,x4的平均数是3,
∴x1+x2+x3+x4=4×3=12,
∴x1﹣1、x2﹣1、x3﹣1、x4﹣1的平均数是:
(x1﹣1+x2﹣1+x3﹣1+x4﹣1)÷4
=(12﹣4)÷4
=2.
故答案为:2.
18.解:设成绩为9环的人数是x,根据题意得:
(7×3+8×4+9x)÷(3+4+x)=8,
解得:x=3,
则成绩为9环的人数是3.
故答案为:3.
19.解:因为7出现了2次,其它数字都只出现一次,所以众数是7;
把数据按从小到大的顺序排列得到2、5、7、7、9,最中间的一个数是7,所以中位数是7;
平均数为(2+5+7+7+9)÷5=6.
故答案为:7,7,6.
20.解:由题意知,错将其中一个数据15输入为105,则多加了105﹣15=90,所以平均数多了90÷30=3.
故填3.
三.解答题
21.解:八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,是抽样调查,故(1)正确;
800名学生的立定跳远成绩是总体,故(2)错误;
每名学生的立定跳远成绩是个体,故(3)正确;
这100名学生的立定跳远成绩是总体的一个样本,故(4)正确;
100是样本容量,故(5)错误.
故说法正确的是(1)(3)(4).
22.解:(1)36÷36%=100(个).
(2)a=100×16%=16(个).
(3)将竞赛成绩从小到大排列后处在第50、51位的数都落在C组,因此中位数落在C组;
(4)500×36%=180(人).
答:该校九年级竞赛成绩达到90分以上(含90分)的学生约有180人.
故答案为:100;16;C组;180.
23.解:(1)这5只生猪的平均重量为=78.4(千克);
(2)根据用样本估计总体的思想可估计这200只生猪每只生猪的平均重量为78.4千克;
根据题意,生猪的价格为11元/kg,
故这200只生猪能卖78.4×11×200=172480(元).
24.解:(1)解法一:500×64%+500×28%=460(份).
答:食堂每天需要准备460份午餐.
解法二:500﹣500×8%=460(份).
答:食堂每天需要准备460份午餐.
(2)①可以估计参加演练的100名职员用餐时间的平均数为:
==19(min),
参加演练的100名职员取餐的人均时间:(min);
可以估计:该公司用餐职员的用餐时间平均为19min,取餐职员取餐时间平均为0.1
min.
根据表格,可以估计第一批职员用餐19min后,空出的座位有:160×60%=96(个).
而第二批职员此时开始排队取餐,取完餐坐满这96个空位所用的时间约为:96×0.1=9.6(min).
根据表格,可以估计:第一批职员用餐19min后,剩下的职员在6min后即可全部结束用餐,因为9.6>6,所以第二批取餐进入用餐区的职员都能保证有座位.
②可以估计140名只取餐的职员,需要14min可取完餐.
可设计时间安排表如下:
时间
取餐、用餐安排
12:00﹣12:19
第一批160名在食堂用餐的职员用餐;仅在食堂取餐的140名职员取餐
12:19﹣13:00
第二批160名在食堂用餐的职员取餐、用餐
13:00﹣
食堂进行消杀工作
25.解:(1)观察条形统计图,
==1.52,
所以这组数据的平均数是1.52,
将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.5,
这组数据的中位数是1.5.
(2)在所抽取的样本中,质量为2.0kg的数量有4只,
=0.08,
所以由样本数据,估计这2500只鸡中,质量为2.0kg的数量约占8%.
2500×8%=200(只).
故质量为2.0kg的约有200只.
26.解:(1)100﹣71=29.
(2)估计这10名同学的平均成绩为90分.把他们成绩超过90的部分记作正数,不足90的部分记作负数.
这10位学生的分数分别记为:+2,+3,﹣2,﹣14,+10,0,﹣19,+7,+2,+1.
90+(2+3﹣2﹣14+10+0﹣19+7+2+1)÷10
=90﹣1
=89.
答:这10名学生的平均成绩是89,我估计的分值与此很接近.
故答案为:29;90.
数据分析》单元测试卷
一.选择题
1.某学校初、高六个年级共有2000名学生,为了了解其视力情况,现采用抽样调查,如果按10%的比例抽样,则样本容量是( )
A.2000
B.10
C.200
D.10%
2.某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=3:2的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是( )
A.43分
B.85分
C.86分
D.170分
3.某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5
B.6
C.0.5
D.﹣6
4.下列问题中,应采用抽样调查的是( )
A.企业招聘,对应聘人员进行面试
B.了解某班学生的身高情况
C.调查春节联欢晚会的收视率
D.了解某校七年级第二学期期末考试各班的数学科平均成绩
5.小明在计算一组数据的方差时,列出的公式如下:s2=,根据公式信息,下列说法中,错误的是( )
A.数据个数是5
B.数据平均数是8
C.数据众数是8
D.数据方差是0
6.为全力抗战疫情,响应政府“停课不停学”号召,东营市教育局发布关于疫情防控期间开展在线课程教学的通知:从2月10日开始,全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2月10日在线答疑问题总个数如下表所示,则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
学科
语文
数学
英语
物理
化学
道法
历史
数量/个
26
28
28
26
24
21
22
A.22
B.24
C.25
D.26
7.有一组数据:﹣5、1、﹣1、5、0、3、4.这组数据的平均数和中位数分别是( )
A.1、1
B.1、5
C.、1
D.、5
8.在某次信息技术能力测试中,“人工智能社团”的八名同学的成绩统计如图所示,由统计图可知这组数据的中位数是( )
A.6分
B.7分
C.8分
D.9分
9.在演讲比赛中,10位选手的成绩统计图如图所示,则这10位选手成绩的众数是( )
A.80
B.85
C.90
D.95
10.在我校“英语课本剧”表演比赛中,初二年级的10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中正确的是( )
A.众数是90
B.平均数是88
C.中位数是85
D.方差是6
二.填空题
11.从一批洗衣机中抽取10台,调查这批洗衣机的使用寿命,在这一抽样调查中,样本容量是
.
12.一组数据2,1,3,1,2,4的中位数是
.
13.已知一组数据1,4,a,3,5,若它的平均数是3,则这组数据的中位数是
.
14.学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如表,请你根据表中的数据选一人参加比赛,最适合的人选是
.(填甲、乙中的一个)
选手
甲
乙
平均数(环)
9.5
9.5
方差
0.035
0.015
15.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是S甲2=36,S乙2=30,则两组成绩的比较稳定的是
.
16.已知一组数据2、a、6、9、12的平均数为7,则a=
.
17.已知一组数据x1、x2、x3、x4的平均数是3,则数据x1﹣1、x2﹣1、x3﹣1、x4﹣1的平均数是
.
18.某次射击训练中,一小组的成绩如下表所示:
环数
7
8
9
人数
3
4
已知该小组的平均成绩为8环,那么成绩为9环的人数是
.
19.数据2,7,5,7,9的众数、中位数、平均数分别是
、
、
.
20.小颖使用计算器求30个数据的平均数时,错将其中一个数据15输入为105,那么由此求出的平均数与实际平均数的差是
.
三.解答题
21.某校八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,指出下列说法中哪些是正确的.
(1)这种调查方式是抽样调查.
(2)800名学生是总体.
(3)每名学生的立定跳远成绩是个体.
(4)这100名学生的立定跳远成绩是总体的一个样本.
(5)100名学生是样本容量.
22.为宣传6月8日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
表1:知识竞赛成绩分组统计表
组别
分数/分
频数
A
60≤x<70
a
B
70≤x<80
20
C
80≤x<90
28
D
90≤x<100
36
(1)本次调查一共随机抽取了
个参赛学生的成绩;
(2)表1中a=
;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是
;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有
人.
23.某养猪场要出售200只生猪,现在市场上生猪的价格为11元/kg,为了估计这200只生猪能卖多少钱,该养猪场从中随机抽取5只,每只猪的重量(单位:kg)如下:76,71,72,86,87.
(1)计算这5只生猪的平均重量;
(2)估计这200只生猪能卖多少钱?
24.某公司有500名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:
①将过去的自主选餐改为提供统一的套餐;
②调查了全体职员复工后的午餐意向,结果如图所示;
③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳160人用餐;
④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;
⑤随机邀请了100名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这100名职员取餐共用时10min,用餐时间(含用餐与回收餐具)如表所示.
为节约时间,食堂决定将第一排用餐职员160人的套餐先摆放在相应餐桌上,并在12:00开始用餐,其他职员则需自行取餐.
用餐时间x/min
人数
15<x≤17
20
17<x≤19
40
19<x≤21
18
21<x≤23
14
23<x≤25
8
(1)食堂每天需要准备多少份午餐?
(2)食堂打算以参加演练的100名职员用餐时间的平均数min为依据进行规划:前一批职员用餐min后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过13:00就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
25.某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图.请根据相关信息,解答下列问题:
(1)求统计的这组数据的平均数、中位数;
(2)根据样本数据,估计这2500只鸡中,质量为2.0kg的约有多少只?
26.下列各数是10名学生在某一次数学考试中的成绩:92,93,88,76,100,90,71,97,92,91
(1)他们的最高分与最低分的差是
;
(2)请先用一个整十的数估计他们的平均成绩是
,把每一名学生的成绩都减去平均成绩的估计值,得到一组新数据,计算出新数据的平均成绩,然后在此基础上计算原成绩的平均成绩,由此检验你的估算能力.
参考答案与试题解析
一.选择题
1.解:2000×10%=200,
故样本容量是200.
故选:C.
2.解:∵(90×3+80×2)÷(3+2)
=430÷5
=86(分)
∴该竞聘教师的最后成绩是86分.
故选:C.
3.解:求15个数据的平均数时,错将其中一个数据15输入为105,即使总和增加了90;那么由此求出的这组数据的平均数与实际平均数的差是90÷15=6.
故选:B.
4.解:A、企业招聘,对应聘人员进行面试应采用全面调查;
B、了解某班学生的身高情况应采用全面调查;
C、调查春节联欢晚会的收视率应采用抽样调查;
D、了解某校七年级第二学期期末考试各班的数学科平均成绩应采用全面调查;
故选:C.
5.解:∵s2=,
∴样本容量是5,故选项A正确,
样本平均数是:=8,故选项B正确,
样本众数是8,故选项C正确,
样本方差是:s2=
[(7﹣8)2+(8﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]=,故选项D错误,
故选:D.
6.解:(26+28+28+26+24+21+22)÷7
=175÷7
=25.
故选:C.
7.解:平均数=(﹣5+1﹣1+5+0+3+4)÷7=1;
把这组数据按从大到小的顺序排列是:﹣5,﹣1,0,1,3,4,5,
故这组数据的中位数是1.
故选:A.
8.解:把这组数据由小到大排列,得4,5,6,7,9,9,9,10,
最中间的两个数是7,9,
所以这组数据的中位数是(7+9)÷2=8(分).
故选:C.
9.解:由题意得:90分出现的次数最多,
∴这10位选手成绩的众数是90(分),
故选:C.
10.解:∵90出现了5次,出现的次数最多,
∴众数是90;
故A正确;
∵平均数是(80×1+85×2+90×5+95×2)÷10=89;
故B错误;
共有10个数,
∴中位数是第5、6个数的平均数,
∴中位数是(90+90)÷2=90;
故C错误;
方差为×[(89﹣80)2+2×(89﹣85)2+2×(89﹣95)2+(89﹣90)2×5]=19,
故D错误.
故选:A.
二.填空题
11.解:从一批洗衣机中抽取10台,调查这批洗衣机的使用寿命,在这一抽样调查中,样本容量是10.
故答案为:10.
12.解:将这组数据从小到大的顺序排列:1,1,2,2,3,4,处于中间位置的两个数是2,2,那么由中位数的定义可知,这组数据的中位数是(2+2)÷2=2.
故答案为:2.
13.解:由题意得(1+4+a+3+5)=3,
解得:a=2,
这组数据按照从小到大的顺序排列为:1,2,3,4,5,
则中位数为3.
故答案为:3.
14.解:因为S甲2=0.035>S乙2=0.015,方差小的为乙,
所以本题中成绩比较稳定的是乙.
所以最适合的人选是乙.
故答案为乙.
15.解:∵S甲2>S乙2,
∴乙的成绩比较稳定,
故答案为:乙.
16.解:由题意知,平均数=(2+a+6+9+12)÷5=7,
所以a=5×7﹣(2+6+9+12)=6.
故答案为:6.
17.解:∵x1,x2,x3,x4的平均数是3,
∴x1+x2+x3+x4=4×3=12,
∴x1﹣1、x2﹣1、x3﹣1、x4﹣1的平均数是:
(x1﹣1+x2﹣1+x3﹣1+x4﹣1)÷4
=(12﹣4)÷4
=2.
故答案为:2.
18.解:设成绩为9环的人数是x,根据题意得:
(7×3+8×4+9x)÷(3+4+x)=8,
解得:x=3,
则成绩为9环的人数是3.
故答案为:3.
19.解:因为7出现了2次,其它数字都只出现一次,所以众数是7;
把数据按从小到大的顺序排列得到2、5、7、7、9,最中间的一个数是7,所以中位数是7;
平均数为(2+5+7+7+9)÷5=6.
故答案为:7,7,6.
20.解:由题意知,错将其中一个数据15输入为105,则多加了105﹣15=90,所以平均数多了90÷30=3.
故填3.
三.解答题
21.解:八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,是抽样调查,故(1)正确;
800名学生的立定跳远成绩是总体,故(2)错误;
每名学生的立定跳远成绩是个体,故(3)正确;
这100名学生的立定跳远成绩是总体的一个样本,故(4)正确;
100是样本容量,故(5)错误.
故说法正确的是(1)(3)(4).
22.解:(1)36÷36%=100(个).
(2)a=100×16%=16(个).
(3)将竞赛成绩从小到大排列后处在第50、51位的数都落在C组,因此中位数落在C组;
(4)500×36%=180(人).
答:该校九年级竞赛成绩达到90分以上(含90分)的学生约有180人.
故答案为:100;16;C组;180.
23.解:(1)这5只生猪的平均重量为=78.4(千克);
(2)根据用样本估计总体的思想可估计这200只生猪每只生猪的平均重量为78.4千克;
根据题意,生猪的价格为11元/kg,
故这200只生猪能卖78.4×11×200=172480(元).
24.解:(1)解法一:500×64%+500×28%=460(份).
答:食堂每天需要准备460份午餐.
解法二:500﹣500×8%=460(份).
答:食堂每天需要准备460份午餐.
(2)①可以估计参加演练的100名职员用餐时间的平均数为:
==19(min),
参加演练的100名职员取餐的人均时间:(min);
可以估计:该公司用餐职员的用餐时间平均为19min,取餐职员取餐时间平均为0.1
min.
根据表格,可以估计第一批职员用餐19min后,空出的座位有:160×60%=96(个).
而第二批职员此时开始排队取餐,取完餐坐满这96个空位所用的时间约为:96×0.1=9.6(min).
根据表格,可以估计:第一批职员用餐19min后,剩下的职员在6min后即可全部结束用餐,因为9.6>6,所以第二批取餐进入用餐区的职员都能保证有座位.
②可以估计140名只取餐的职员,需要14min可取完餐.
可设计时间安排表如下:
时间
取餐、用餐安排
12:00﹣12:19
第一批160名在食堂用餐的职员用餐;仅在食堂取餐的140名职员取餐
12:19﹣13:00
第二批160名在食堂用餐的职员取餐、用餐
13:00﹣
食堂进行消杀工作
25.解:(1)观察条形统计图,
==1.52,
所以这组数据的平均数是1.52,
将这组数据按从小到大的顺序排列,其中处于中间的两个数都是1.5,
这组数据的中位数是1.5.
(2)在所抽取的样本中,质量为2.0kg的数量有4只,
=0.08,
所以由样本数据,估计这2500只鸡中,质量为2.0kg的数量约占8%.
2500×8%=200(只).
故质量为2.0kg的约有200只.
26.解:(1)100﹣71=29.
(2)估计这10名同学的平均成绩为90分.把他们成绩超过90的部分记作正数,不足90的部分记作负数.
这10位学生的分数分别记为:+2,+3,﹣2,﹣14,+10,0,﹣19,+7,+2,+1.
90+(2+3﹣2﹣14+10+0﹣19+7+2+1)÷10
=90﹣1
=89.
答:这10名学生的平均成绩是89,我估计的分值与此很接近.
故答案为:29;90.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
