2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步能力提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步能力提升训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 365.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册《1.3正方形的性质与判定》
同步能力提升训练(附答案)
1.如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
A.
B.
C.
D.
2.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75°
B.60°
C.55°
D.45°
3.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )
A.2
B.3
C.4
D.5
4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
5.下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形
B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形
D.对角线相等的菱形是正方形
6.如图,点E在正方形ABCD的对角线AC上,若AE=AB,则∠EBC的度数为( )
A.22.5°
B.30°
C.45°
D.67.5°
7.如图正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45°
B.55°
C.60°
D.75°
8.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.1
B.
C.4﹣2
D.3﹣4
9.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30
B.34
C.36
D.40
10.如图,在正方形ABCD中,AB=2.E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A.
B.1
C.
D.2
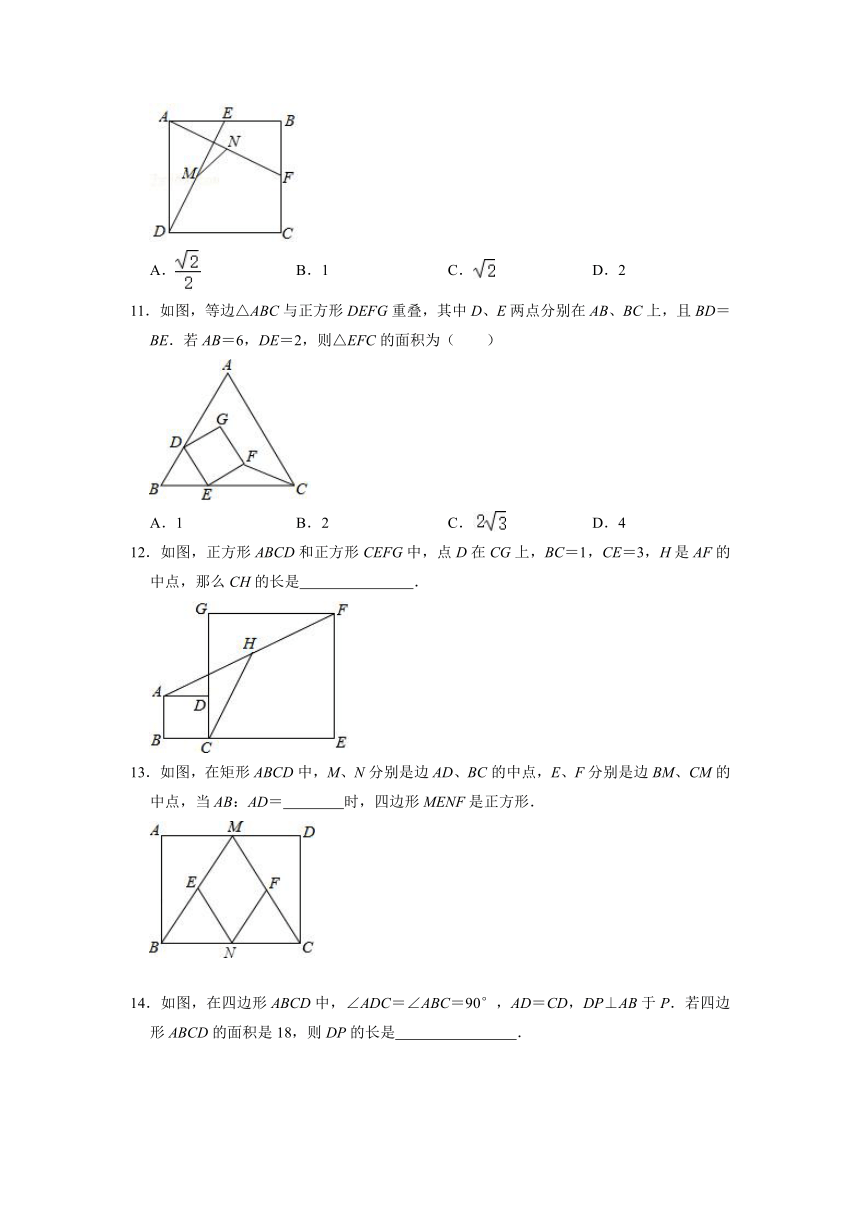
11.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1
B.2
C.
D.4
12.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
.
13.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=
时,四边形MENF是正方形.
14.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是
.
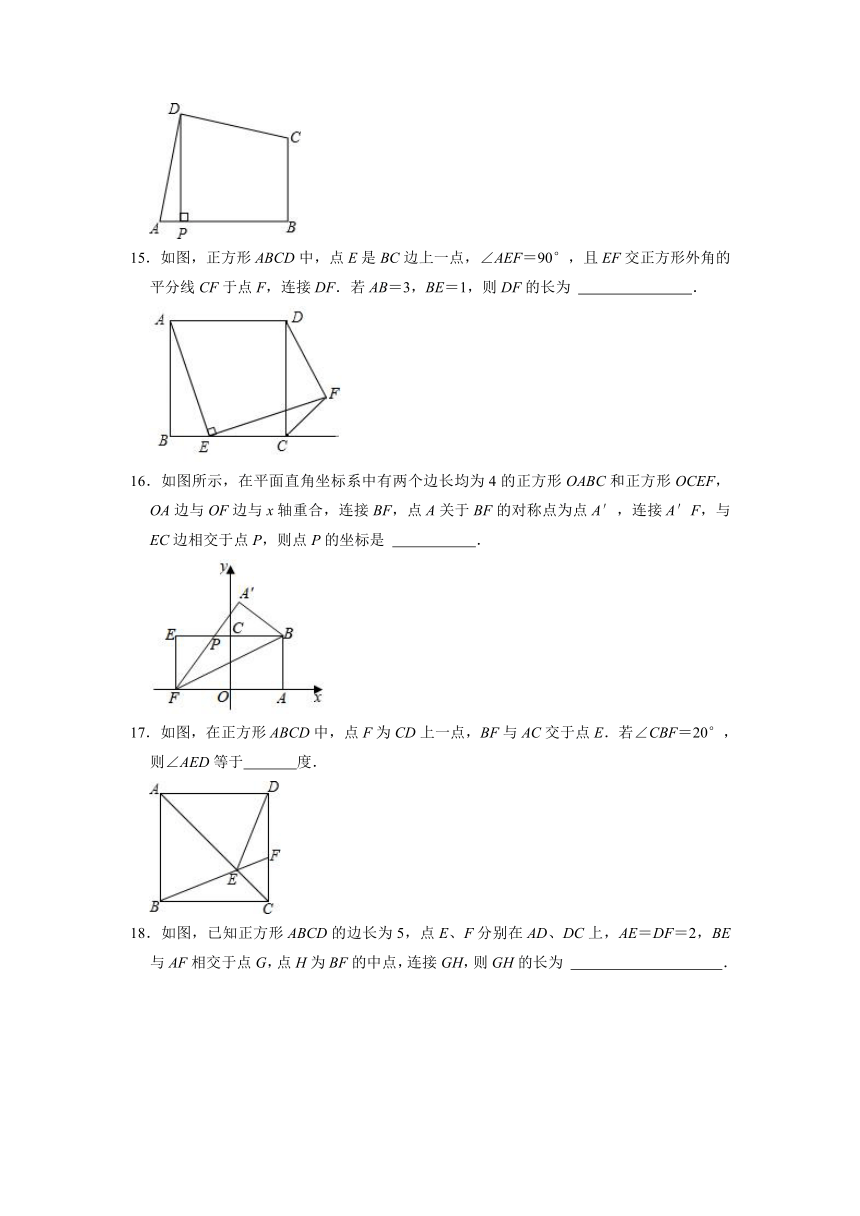
15.如图,正方形ABCD中,点E是BC边上一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,连接DF.若AB=3,BE=1,则DF的长为
.
16.如图所示,在平面直角坐标系中有两个边长均为4的正方形OABC和正方形OCEF,OA边与OF边与x轴重合,连接BF,点A关于BF的对称点为点A′,连接A′F,与EC边相交于点P,则点P的坐标是
.
17.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于
度.
18.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为
.
19.如图,在四边形ABCD中,AD∥BC(BC>AD),∠D=90°,∠ABE=45°,BC=CD,若AE=5,CE=2,则BC的长度为
.
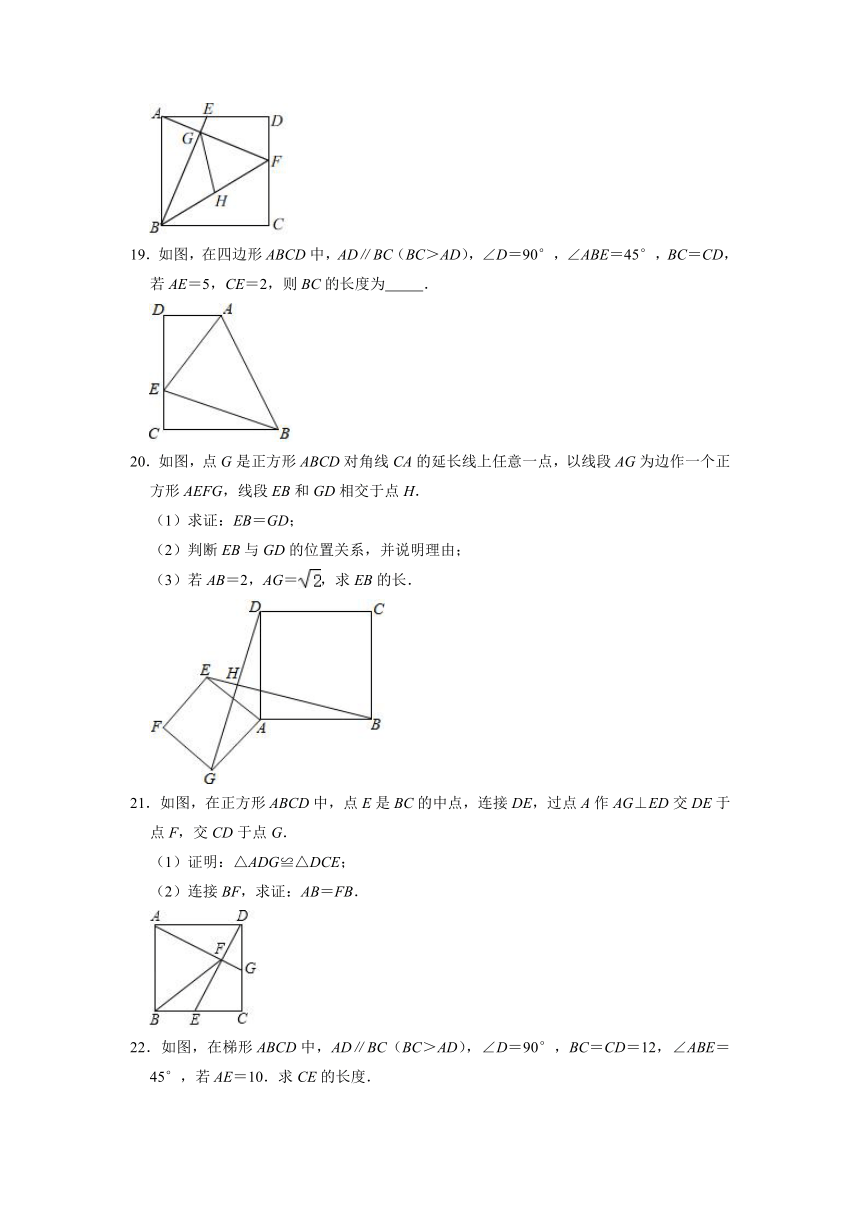
20.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=,求EB的长.
21.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,求证:AB=FB.
22.如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
23.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
24.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
参考答案
1.解:连接BP,过C作CM⊥BD,
∵S△BCE=S△BPE+S△BPC
=BC×PQ×+BE×PR×
=BC×(PQ+PR)×
=BE×CM×,
BC=BE,
∴PQ+PR=CM,
∵BE=BC=1,且正方形对角线BD=BC=,
又∵BC=CD,CM⊥BD,
∴M为BD中点,又△BDC为直角三角形,
∴CM=BD=,
即PQ+PR值是.
故选:D.
2.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
3.解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,
∴DF=BF′,∠DAF=∠BAF′,
∴∠EAF′=45°,
在△FAE和△EAF′中,
,
∴△FAE≌△EAF′(SAS),
∴EF=EF′,
∵△ECF的周长为4,
∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,
∴2BC=4,
∴BC=2.
故选:A.
4.解:A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
故选:B.
5.解:A、一组同旁内角相等的平行四边形是矩形,正确;
B、一组邻边相等的菱形是正方形,错误;
C、有三个角是直角的四边形是矩形,正确;
D、对角线相等的菱形是正方形,正确.
故选:B.
6.解:∵四边形ABCD是正方形,
∴∠BAC=∠BCA=45°,∠ABC=90°,
∵AB=AE,
∴∠ABE=∠AEB=67.5°,
∴∠EBC=22.5°,
故选:A.
7.解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故选:C.
8.解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4,
∴BE=BD﹣DE=4﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF=BE=×(4﹣4)=4﹣2.
故选:C.
9.解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
10.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故选:B.
11.解:过F作FQ⊥BC于Q,则∠FQE=90°,
∵△ABC是等边三角形,AB=6,
∴BC=AB=6,∠B=60°,
∵BD=BE,DE=2,
∴△BED是等边三角形,且边长为2,
∴BE=DE=2,∠BED=60°,
∴CE=BC﹣BE=4,
∵四边形DEFG是正方形,DE=2,
∴EF=DE=2,∠DEF=90°,
∴∠FEC=180°﹣60°﹣90°=30°,
∴QF=EF=1,
∴△EFC的面积为==2,
故选:B.
12.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
13.解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.
14.解:如图,过点D作DE⊥DP交BC的延长线于E,
∵∠ADC=∠ABC=90°,
∴四边形DPBE是矩形,
∵∠CDE+∠CDP=90°,∠ADC=90°,
∴∠ADP+∠CDP=90°,
∴∠ADP=∠CDE,
∵DP⊥AB,
∴∠APD=90°,
∴∠APD=∠E=90°,
在△ADP和△CDE中,
,
∴△ADP≌△CDE(AAS),
∴DE=DP,四边形ABCD的面积=四边形DPBE的面积=18,
∴矩形DPBE是正方形,
∴DP==3.
故答案为:3.
15.解:过点F作FG⊥CD于点G,FH⊥BC延长线于点H,如图,
∵四边形ABCD是正方形,
∴∠AB=BC=CD=3,∠DCH=90°,
∵FC是∠DCH平分线,
∴FG=FH,
∴矩形CGFH为正方形,
∴HC=FH,
∵∠BAE+∠AEB=∠AEB+∠FEH=90°,
∴∠BAE=∠FEH,
∵∠ABE=∠EHF,
∴m=1,
∴FG=CH=CG=1,DG=3﹣1=2,
在Rt△DGF中,DF==,
故答案为.
16.解:∵正方形OABC和正方形OCEF的边长均为4,
∴EF=AB,
∵△FAB与△FA'B关于直线BF对称,
∴AB=A'B,∠A'=∠A=90°
∵∠EPF=∠A'PB,
∴△EPF≌△A'PB(AAS),
∴PB=PF,
设PE=a,则PF﹣PB=8﹣a,
在Rt△EPF中,EF2+PE2=PF2,
即42+a2=(8﹣a)2,
解得a=3,
∴CP=4﹣3=1,
∴点P坐标为(﹣1,4),
故答案为(﹣1,4).
17.解:∵正方形ABCD,
∴AB=AD,∠BAE=∠DAE,
在△ABE与△ADE中,
,
∴△ABE≌△ADE(SAS),
∴∠AEB=∠AED,∠ABE=∠ADE,
∵∠CBF=20°,
∴∠ABE=70°,
∴∠AED=∠AEB=180°﹣45°﹣70°=65°,
故答案为:65
18.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=5、CF=CD﹣DF=5﹣2=3,
∴BF==,
∴GH=BF=,
故答案为:.
19.解:过点B作BF⊥AD于点F,延长DF使FG=EC,连接BG,
∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,BF⊥AD
∴四边形CDFB是矩形
∵BC=CD
∴四边形CDFB是正方形
∴CD=BC=DF=BF,∠CBF=90°=∠C=∠BFG,
∵BC=BF,∠BFG=∠C=90°,CE=FG
∴△BCE≌△BFG(SAS)
∴BE=BG,∠CBE=∠FBG
∵∠ABE=45°,
∴∠CBE+∠ABF=45°,
∴∠ABF+∠FBG=45°=∠ABG
∴∠ABG=∠ABE,且AB=AB,BE=BG
∴△ABE≌△ABG(SAS)
∴AE=AG=5,
∴AF=AG﹣FG=5﹣2=3
在Rt△ADE中,AE2=AD2+DE2,
∴25=(DF﹣3)2+(DF﹣2)2,
∴DF=6,DF=﹣1(不合题意)
∴BC=6
故答案为:6
20.解:(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=90°,
在△GAD和△EAB中
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:如图1,AD,BE的交点记作点M,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:如图2,连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,OA=OB,
∴BD⊥CG,
∵AB=AD=2,
在Rt△ABD中,DB=,
OD=DB=
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA=,
即OG=OA+AG=+=2,
∴EB=GD=.
21.证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,
∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
22.解:过B作DA的垂线交DA的延长线于M,M为垂足,
延长DM到G,使MG=CE,连接BG,
易知四边形BCDM是正方形,
则△BEC与△BGM中,
,
∴△BEC≌△BMG(SAS),
∴∠MBG=∠CBE,BE=BG,
∵∠ABE=45°,
∴∠CBE+∠ABM=∠MBG+∠ABM=45°,
即∠ABE=∠ABG=45°,
在△ABE与△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AG=AE=10,
设CE=x,则AM=10﹣x,
AD=12﹣(10﹣x)=2+x,DE=12﹣x,
在Rt△ADE中,AE2=AD2+DE2,
∴100=(x+2)2+(12﹣x)2,
即x2﹣10x+24=0;
解得:x1=4,x2=6.
故CE的长为4或6.
23.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,(3分)
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,(5分)
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
24.(1)证明:∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)证明:延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,
∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
同步能力提升训练(附答案)
1.如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
A.
B.
C.
D.
2.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75°
B.60°
C.55°
D.45°
3.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )
A.2
B.3
C.4
D.5
4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
5.下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形
B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形
D.对角线相等的菱形是正方形
6.如图,点E在正方形ABCD的对角线AC上,若AE=AB,则∠EBC的度数为( )
A.22.5°
B.30°
C.45°
D.67.5°
7.如图正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45°
B.55°
C.60°
D.75°
8.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.1
B.
C.4﹣2
D.3﹣4
9.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30
B.34
C.36
D.40
10.如图,在正方形ABCD中,AB=2.E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A.
B.1
C.
D.2
11.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )
A.1
B.2
C.
D.4
12.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
.
13.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=
时,四边形MENF是正方形.
14.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是
.
15.如图,正方形ABCD中,点E是BC边上一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,连接DF.若AB=3,BE=1,则DF的长为
.
16.如图所示,在平面直角坐标系中有两个边长均为4的正方形OABC和正方形OCEF,OA边与OF边与x轴重合,连接BF,点A关于BF的对称点为点A′,连接A′F,与EC边相交于点P,则点P的坐标是
.
17.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于
度.
18.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为
.
19.如图,在四边形ABCD中,AD∥BC(BC>AD),∠D=90°,∠ABE=45°,BC=CD,若AE=5,CE=2,则BC的长度为
.
20.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=,求EB的长.
21.如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,求证:AB=FB.
22.如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
23.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
24.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
参考答案
1.解:连接BP,过C作CM⊥BD,
∵S△BCE=S△BPE+S△BPC
=BC×PQ×+BE×PR×
=BC×(PQ+PR)×
=BE×CM×,
BC=BE,
∴PQ+PR=CM,
∵BE=BC=1,且正方形对角线BD=BC=,
又∵BC=CD,CM⊥BD,
∴M为BD中点,又△BDC为直角三角形,
∴CM=BD=,
即PQ+PR值是.
故选:D.
2.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
3.解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,
∴DF=BF′,∠DAF=∠BAF′,
∴∠EAF′=45°,
在△FAE和△EAF′中,
,
∴△FAE≌△EAF′(SAS),
∴EF=EF′,
∵△ECF的周长为4,
∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,
∴2BC=4,
∴BC=2.
故选:A.
4.解:A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
故选:B.
5.解:A、一组同旁内角相等的平行四边形是矩形,正确;
B、一组邻边相等的菱形是正方形,错误;
C、有三个角是直角的四边形是矩形,正确;
D、对角线相等的菱形是正方形,正确.
故选:B.
6.解:∵四边形ABCD是正方形,
∴∠BAC=∠BCA=45°,∠ABC=90°,
∵AB=AE,
∴∠ABE=∠AEB=67.5°,
∴∠EBC=22.5°,
故选:A.
7.解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故选:C.
8.解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4,
∴BE=BD﹣DE=4﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF=BE=×(4﹣4)=4﹣2.
故选:C.
9.解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH==,
∴四边形EFGH的面积是:×=34,
故选:B.
10.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故选:B.
11.解:过F作FQ⊥BC于Q,则∠FQE=90°,
∵△ABC是等边三角形,AB=6,
∴BC=AB=6,∠B=60°,
∵BD=BE,DE=2,
∴△BED是等边三角形,且边长为2,
∴BE=DE=2,∠BED=60°,
∴CE=BC﹣BE=4,
∵四边形DEFG是正方形,DE=2,
∴EF=DE=2,∠DEF=90°,
∴∠FEC=180°﹣60°﹣90°=30°,
∴QF=EF=1,
∴△EFC的面积为==2,
故选:B.
12.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
13.解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.
14.解:如图,过点D作DE⊥DP交BC的延长线于E,
∵∠ADC=∠ABC=90°,
∴四边形DPBE是矩形,
∵∠CDE+∠CDP=90°,∠ADC=90°,
∴∠ADP+∠CDP=90°,
∴∠ADP=∠CDE,
∵DP⊥AB,
∴∠APD=90°,
∴∠APD=∠E=90°,
在△ADP和△CDE中,
,
∴△ADP≌△CDE(AAS),
∴DE=DP,四边形ABCD的面积=四边形DPBE的面积=18,
∴矩形DPBE是正方形,
∴DP==3.
故答案为:3.
15.解:过点F作FG⊥CD于点G,FH⊥BC延长线于点H,如图,
∵四边形ABCD是正方形,
∴∠AB=BC=CD=3,∠DCH=90°,
∵FC是∠DCH平分线,
∴FG=FH,
∴矩形CGFH为正方形,
∴HC=FH,
∵∠BAE+∠AEB=∠AEB+∠FEH=90°,
∴∠BAE=∠FEH,
∵∠ABE=∠EHF,
∴m=1,
∴FG=CH=CG=1,DG=3﹣1=2,
在Rt△DGF中,DF==,
故答案为.
16.解:∵正方形OABC和正方形OCEF的边长均为4,
∴EF=AB,
∵△FAB与△FA'B关于直线BF对称,
∴AB=A'B,∠A'=∠A=90°
∵∠EPF=∠A'PB,
∴△EPF≌△A'PB(AAS),
∴PB=PF,
设PE=a,则PF﹣PB=8﹣a,
在Rt△EPF中,EF2+PE2=PF2,
即42+a2=(8﹣a)2,
解得a=3,
∴CP=4﹣3=1,
∴点P坐标为(﹣1,4),
故答案为(﹣1,4).
17.解:∵正方形ABCD,
∴AB=AD,∠BAE=∠DAE,
在△ABE与△ADE中,
,
∴△ABE≌△ADE(SAS),
∴∠AEB=∠AED,∠ABE=∠ADE,
∵∠CBF=20°,
∴∠ABE=70°,
∴∠AED=∠AEB=180°﹣45°﹣70°=65°,
故答案为:65
18.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=5、CF=CD﹣DF=5﹣2=3,
∴BF==,
∴GH=BF=,
故答案为:.
19.解:过点B作BF⊥AD于点F,延长DF使FG=EC,连接BG,
∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,BF⊥AD
∴四边形CDFB是矩形
∵BC=CD
∴四边形CDFB是正方形
∴CD=BC=DF=BF,∠CBF=90°=∠C=∠BFG,
∵BC=BF,∠BFG=∠C=90°,CE=FG
∴△BCE≌△BFG(SAS)
∴BE=BG,∠CBE=∠FBG
∵∠ABE=45°,
∴∠CBE+∠ABF=45°,
∴∠ABF+∠FBG=45°=∠ABG
∴∠ABG=∠ABE,且AB=AB,BE=BG
∴△ABE≌△ABG(SAS)
∴AE=AG=5,
∴AF=AG﹣FG=5﹣2=3
在Rt△ADE中,AE2=AD2+DE2,
∴25=(DF﹣3)2+(DF﹣2)2,
∴DF=6,DF=﹣1(不合题意)
∴BC=6
故答案为:6
20.解:(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,∠DAB=90°,
在△GAD和△EAB中
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:如图1,AD,BE的交点记作点M,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:如图2,连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,OA=OB,
∴BD⊥CG,
∵AB=AD=2,
在Rt△ABD中,DB=,
OD=DB=
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA=,
即OG=OA+AG=+=2,
∴EB=GD=.
21.证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,
∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
22.解:过B作DA的垂线交DA的延长线于M,M为垂足,
延长DM到G,使MG=CE,连接BG,
易知四边形BCDM是正方形,
则△BEC与△BGM中,
,
∴△BEC≌△BMG(SAS),
∴∠MBG=∠CBE,BE=BG,
∵∠ABE=45°,
∴∠CBE+∠ABM=∠MBG+∠ABM=45°,
即∠ABE=∠ABG=45°,
在△ABE与△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AG=AE=10,
设CE=x,则AM=10﹣x,
AD=12﹣(10﹣x)=2+x,DE=12﹣x,
在Rt△ADE中,AE2=AD2+DE2,
∴100=(x+2)2+(12﹣x)2,
即x2﹣10x+24=0;
解得:x1=4,x2=6.
故CE的长为4或6.
23.证明:(1)∵四边形ABCD是正方形,
∴∠DAB=90°,AC平分∠DAB,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形MANP是矩形,
∵AC平分∠DAB,PM⊥AD,PN⊥AB,
∴PM=PN,(3分)
∴四边形MANP是正方形;
(2)∵四边形ABCD是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE+∠EPN=∠NPB+∠EPN=90°,
∴∠MPE=∠NPB,(5分)
在△EPM和△BPN中,
∵,
∴△EPM≌△BPN(ASA),
∴EM=BN.
24.(1)证明:∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)证明:延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,
∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
