2020-2021学年山东省济宁市太白湖新区北湖区六年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省济宁市太白湖新区北湖区六年级(下)期末数学试卷(五四学制)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 839.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览





文档简介
2020-2021学年山东省济宁市太白湖新区北湖区六年级(下)期末数学试卷(五四学制)
一、选择题(共10小题).
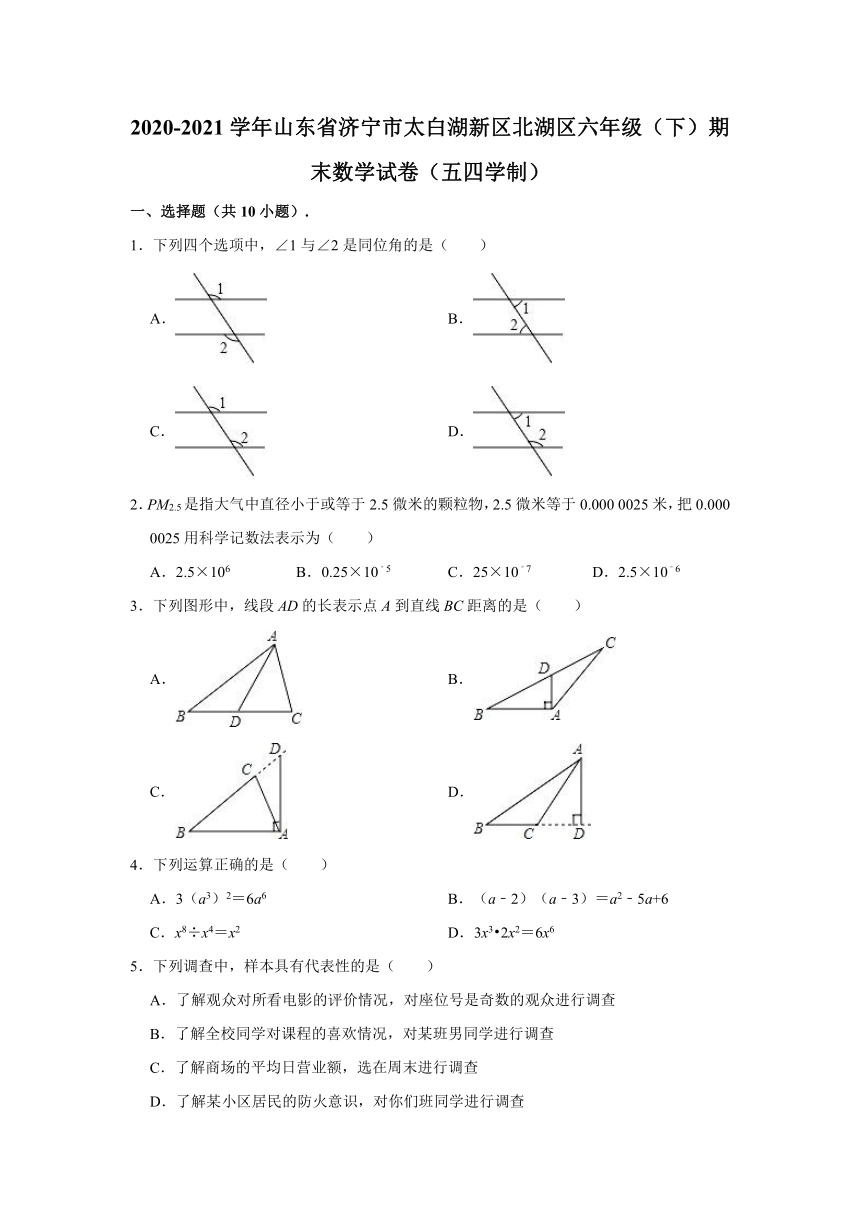
1.下列四个选项中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000
0025米,把0.000
0025用科学记数法表示为( )
A.2.5×106
B.0.25×10﹣5
C.25×10﹣7
D.2.5×10﹣6
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
4.下列运算正确的是( )
A.3(a3)2=6a6
B.(a﹣2)(a﹣3)=a2﹣5a+6
C.x8÷x4=x2
D.3x3?2x2=6x6
5.下列调查中,样本具有代表性的是( )
A.了解观众对所看电影的评价情况,对座位号是奇数的观众进行调查
B.了解全校同学对课程的喜欢情况,对某班男同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解某小区居民的防火意识,对你们班同学进行调查
6.如图,点C在线段AB上,AB=10cm,AC=4cm,点D是BC的中点,则BD=( )
A.2cm
B.3cm
C.5cm
D.6cm
7.某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计,下面判断中正确的有( )
①这种调查的方式是抽样调查;
②800名学生的数学成绩是总体;
③每名学生的期中数学成绩是个体;
④100名学生的数学成绩是总体的一个样本.
A.1个
B.2个
C.3个
D.4个
8.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有( )
A.10人
B.12人
C.8人
D.9人
9.已知
a+b=3,ab=1,则a2+b2的值为( )
A.7
B.9
C.5
D.8
10.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,如图是公司为居民绘制的水费y(元)随当月用水量x(吨)变化而变化的图象,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家7月份缴水费30元,则该用户当月用水18.5吨
D.若小明家3月份用水14吨,则应缴水费23元
二、填空题(本大题满分15分,每小题3分,请你将答案填写在答题卡中)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是
.
12.如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2=
.
13.如图,小明从A地前往B地,到达后立刻返回,他与A地的距离y(千米)和所用时间x(小时)之间的关系如图所示,则小明出发5小时后距A地
千米.
14.计算:()2020×1.52021×(﹣1)2020=
.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第n个图形黑色棋子个数y与n的关系式为
.
三、解答题(本大题满分55分,解答要写出必要的文字说明或推演步骤)
16.计算:
(1)(π﹣3.14)0﹣+(﹣2)3;
(2)(3x+2)(2x﹣1).
17.先化简,再求值:
(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x),其中x=,y=2.
18.如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求:
(1)∠COD的度数;
(2)求∠MON的度数.
19.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表:
节目
人数(名)
百分比
最强大脑
a
10%
朗读者
15
b%
中国诗词大会
c
40%
出彩中国
10
20%
根据以上提供的信息,解答下列问题:
(1)x=
,a=
,b=
;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
20.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵
,
∴∠CDA=90°,∠DAB=90°(
).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴
(
),
∴DF∥AE(
).
21.某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,求A级所占百分比;
(2)在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数.
22.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
23.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
24.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
参考答案
一、选择题(本大题满分30分,每小题3分.每小题只有一个符合题意的选项,请你将正确选项的代号填在答题卡内)
1.下列四个选项中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
【分析】根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角可得答案.
解:根据同位角定义可得C中∠1,∠2是同位角,
故选:C.
2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000
0025米,把0.000
0025用科学记数法表示为( )
A.2.5×106
B.0.25×10﹣5
C.25×10﹣7
D.2.5×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000
0025=2.5×10﹣6,
故选:D.
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
【分析】点到直线的距离是指垂线段的长度.
解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
4.下列运算正确的是( )
A.3(a3)2=6a6
B.(a﹣2)(a﹣3)=a2﹣5a+6
C.x8÷x4=x2
D.3x3?2x2=6x6
【分析】根据整式的运算法则即可求出答案.
解:A、原式=3a6,故A错误.
C、原式=x4,故C错误,
D、原式=6x5,故D错误.
故选:B.
5.下列调查中,样本具有代表性的是( )
A.了解观众对所看电影的评价情况,对座位号是奇数的观众进行调查
B.了解全校同学对课程的喜欢情况,对某班男同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解某小区居民的防火意识,对你们班同学进行调查
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
解:A、了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查,调查具有代表性、广泛性,故符合题意;
B、了解全校同学对课程的喜欢情况,对某班男同学进行调查,不具代表性、广泛性,故不符合题意;
C、了解商场的平均日营业额,选在周末进行调查,调查不具有代表性、广泛性,故不符合题意;
D、了解某小区居民的防火意识,对你们班同学进行调查,调查不具代表性、广泛性,故不符合题意;
故选:A.
6.如图,点C在线段AB上,AB=10cm,AC=4cm,点D是BC的中点,则BD=( )
A.2cm
B.3cm
C.5cm
D.6cm
【分析】根据已知条件先求出BC,再根据中点的性质求出BD即可.
解:∵AB=10cm,AC=4cm,
∴BC=AB﹣AC=6cm,
∵点D是BC的中点,
∴BD=BC=3cm.
故选:B.
7.某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计,下面判断中正确的有( )
①这种调查的方式是抽样调查;
②800名学生的数学成绩是总体;
③每名学生的期中数学成绩是个体;
④100名学生的数学成绩是总体的一个样本.
A.1个
B.2个
C.3个
D.4个
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体.本题考察的对象是我校八年级学生期中数学考试成绩,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
解:①很明显,这种调查方式是抽样调查.故正确;
②总体是七年级800名学生期中数学考试成绩.故错误;
③个体是七年级每个学生的期中数学考试成绩,这个说法正确.正确;
④100名学生的期中数学考试成绩才是总体的一个样本.故错误;
故正确的说法有①③共2个.
故选:B.
8.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有( )
A.10人
B.12人
C.8人
D.9人
【分析】根据A型血的有20人,所占的百分比是40%即可求得班级总人数,根据AB型所对应的扇形圆心角的度数求得对应的百分比,则用总人数乘以O型血所对应的百分比即可求解.
解:全班的人数是:20÷40%=50(人),
则O型血的人数是:50(1﹣40%﹣30%﹣10%)=10(人).
故选:A.
9.已知
a+b=3,ab=1,则a2+b2的值为( )
A.7
B.9
C.5
D.8
【分析】根据a2+b2=(a+b)2﹣2ab代入即可求解.
解:∵a+b=3,ab=1
∴a2+b2=(a+b)2﹣2ab
=32﹣2×1=7;
故选:A.
10.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,如图是公司为居民绘制的水费y(元)随当月用水量x(吨)变化而变化的图象,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家7月份缴水费30元,则该用户当月用水18.5吨
D.若小明家3月份用水14吨,则应缴水费23元
【分析】利用(10,15),(20,35)两点求出a,b的值即可.
解:由图象可知,a=15÷10=1.5;
b==2;
缴水费30元,则该用户当月用水为:10+(30﹣15)÷2=17.5(吨);
用水14吨,则应缴水费:1.5×10+2×(14﹣10)=15+8=23(元).
故结论错误的是选项C.
故选:C.
二、填空题(本大题满分15分,每小题3分,请你将答案填写在答题卡中)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 t .
【分析】根据函数的定义:设x和y是两个变量,对于x的每一个值,y都有唯一确定的值和它对应,我们就说y是x的函数,其中x是自变量.据此解答即可.
解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
12.如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2= 55° .
【分析】根据平角的定义求出∠3,再根据两直线平行,同位角相等可得∠2=∠3.
解:如图,∵∠1=35°,
∴∠3=180°﹣35°﹣90°=55°,
∵a∥b,
∴∠2=∠3=55°.
故答案为:55°.
13.如图,小明从A地前往B地,到达后立刻返回,他与A地的距离y(千米)和所用时间x(小时)之间的关系如图所示,则小明出发5小时后距A地
200 千米.
【分析】根据函数图象中的数据可以求得当4≤x≤10时,y与x的函数关系式,然后将x=5代入求得函数解析式,即可解答本题.
解:设当4≤x≤10时,y与x的函数关系式为y=kx+b,
则,
解得:
∴当4≤x≤10时,y与x的函数关系式为y=﹣40x+400,
∴当x=5时,y=﹣40×5+400=200,
即小明出发5小时后距A地200千米,
故答案为:200.
14.计算:()2020×1.52021×(﹣1)2020= .
【分析】逆向运用积的乘方运算法则以及有理数的乘方的定义计算即可.
解:()2020×1.52021×(﹣1)2020
=
=
=
=.
故答案为:.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第n个图形黑色棋子个数y与n的关系式为
y=3n+3 .
【分析】根据图中所给的黑色棋子的颗数,找出其中的规律,用含n的代数式表示即可求出答案.
解:第1个图形有6颗黑色棋子,
第2个图形有9颗黑色棋子,
第3个图形有12颗黑色棋子,
第4个图形有15颗黑色棋子,
第5个图形有18颗黑色棋子,
?
第n个图形有棋子个数y=6+3(n﹣1)=3n+3,
故答案为:y=3n+3.
三、解答题(本大题满分55分,解答要写出必要的文字说明或推演步骤)
16.计算:
(1)(π﹣3.14)0﹣+(﹣2)3;
(2)(3x+2)(2x﹣1).
【分析】(1)根据零指数幂的性质,负整数指数幂的性质,乘方的定义分别求解各项的值,再合并即可求解;
(2)根据多项式乘多项式的运算法则计算可求解.
解:(1)原式=1﹣9﹣8
=﹣16;
(2)原式=6x2﹣3x+4x﹣2
=6x2+x﹣2.
17.先化简,再求值:
(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x),其中x=,y=2.
【分析】先根据整式的乘法法则和乘法公式算乘法,再合并同类项,最后代入求出即可.
解:(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x)
=x2﹣4y2+x2+4xy+4y2﹣2xy+x2
=3x2+2xy,
当x=,y=2时,原式3×()2+2××2=2.
18.如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求:
(1)∠COD的度数;
(2)求∠MON的度数.
【分析】(1)根据∠COD=∠AOB﹣∠AOC﹣∠BOD,代入即可求解;
(2)先根据角平分线的意义求出∠COM和∠DON,再根据∠MON=∠COM+∠DON+∠COD,即可求解.
解:(1)因为∠AOC=30°,∠BOD=60°,
所以∠COD═∠AOB﹣∠AOC﹣∠BOD=180°﹣30°﹣60°=90°
(3)因所OM,ON分别平分∠AOC,∠BOD
所以∠COM=15°,
∠DON=30°,
所以∠NOM=∠COM+∠DON+∠COD=15°+30°+90°=135°.
19.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表:
节目
人数(名)
百分比
最强大脑
a
10%
朗读者
15
b%
中国诗词大会
c
40%
出彩中国
10
20%
根据以上提供的信息,解答下列问题:
(1)x= 50 ,a= 5 ,b= 30 ;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
【分析】(1)根据喜爱出彩中国的人数和所占的百分比可以求得x的值,然后根据统计表中的数据,即可得到a和b的值;
(2)根据(1)中的结果可以得到c的值,从而可以将条形统计图补充完整;
(3)根据统计表中的数据,可以计算出该校最喜爱《中国诗词大会》节目的学生有多少名.
解:(1)x=10÷20%=50,
a=50×10%=5,
b%=15÷50×100%=30%,
故答案为:50,5,30;
(2)c=50×40%=20,
补全的条形统计图如右图所示;
(3)5000×40%=2000(名),
答:该校最喜爱《中国诗词大会》节目的学生有2000名.
20.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ CD⊥DA,DA⊥AB, ,
∴∠CDA=90°,∠DAB=90°(
垂直定义 ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ∠3=∠4 (
等角的余角相等 ),
∴DF∥AE(
内错角相等,两直线平行 ).
【分析】先根据垂直的定义,得到∠1+∠3=90°,∠2+∠4=90°,再根据等角的余角相等,得出∠3=∠4,最后根据内错角相等,两直线平行进行判定即可.
【解答】证明:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°,(垂直定义)
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴∠3=∠4,(等角的余角相等)
∴DF∥AE.(内错角相等,两直线平行)
故答案为:CD⊥DA,DA⊥AB,垂直定义,∠3=∠4,等角的余角相等,内错角相等,两直线平行.
21.某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,求A级所占百分比;
(2)在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数.
【分析】(1)根据A级对应的圆心角的度数可以求得A级所占百分比;
(2)根据A级对应的圆心角的度数和对应的频数,可以求得本次调查的总人数,然后即可求得D级的人数,从而可以将频数分布直方图补充完整;
(3)根据频数分布直方图中的数据,可以计算出D级对应的圆心角的度数,
解:(1)∵A级所在扇形的圆心角的度数为90°,
∴A级所占百分比为;
(2)∵A级有25人,占25%,
∴抽查的总人数为25÷25%=100(人),
∴D级有100﹣20﹣40﹣25=15(人),
补全的频数分布图如右图所示;
(3)D级的圆心角为:,
即D级对应的圆心角的度数为54°.
22.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
【分析】根据平行线的性质和角平分线的定义解答即可.
解:∵AB∥CD,∠FGB=154°,
∴∠GFD=180°﹣∠FGB=180°﹣154°=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=2×26°=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
23.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
【分析】(1)由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少6L,据此可得t与Q的关系式;
(2)求汽车行驶5h后,油箱中的剩余油量即是求当t=5时,Q的值;
(3)贮满50L汽油的汽车,理论上最多能行驶几小时即是求当Q=50时,t的值.
解:(1)Q=100﹣6t;
(2)当t=5时,Q=100﹣6×5=70.
答:汽车行驶5h后,油箱中的剩余油量是70L;
(3)当Q=50时,50=100﹣6t,
6t=50,
解得:t=,
100×=km.
答:该车最多能行驶km.
24.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 兔子 (填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是 1500 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
【分析】(1)利用乌龟始终运动,中间没有停留,而兔子中间有休息的时刻,即可得出折线OABC的意义和全程的距离;
(2)根据图象中点A、D实际意义可得速度;
(3)根据乌龟的速度及兔子睡觉时的路程即可得;
(4)利用兔子的速度,求出兔子走完全程的时间,再求解即可.
解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
由图象可知:赛跑的全过程为1500米;
故答案为:兔子,1500;
(2)结合图象得出:
兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
(3)700÷30=(分钟),
所以乌龟用了分钟追上了正在睡觉的兔子.
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).
所以兔子中间停下睡觉用了46.5分钟.
一、选择题(共10小题).
1.下列四个选项中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000
0025米,把0.000
0025用科学记数法表示为( )
A.2.5×106
B.0.25×10﹣5
C.25×10﹣7
D.2.5×10﹣6
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
4.下列运算正确的是( )
A.3(a3)2=6a6
B.(a﹣2)(a﹣3)=a2﹣5a+6
C.x8÷x4=x2
D.3x3?2x2=6x6
5.下列调查中,样本具有代表性的是( )
A.了解观众对所看电影的评价情况,对座位号是奇数的观众进行调查
B.了解全校同学对课程的喜欢情况,对某班男同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解某小区居民的防火意识,对你们班同学进行调查
6.如图,点C在线段AB上,AB=10cm,AC=4cm,点D是BC的中点,则BD=( )
A.2cm
B.3cm
C.5cm
D.6cm
7.某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计,下面判断中正确的有( )
①这种调查的方式是抽样调查;
②800名学生的数学成绩是总体;
③每名学生的期中数学成绩是个体;
④100名学生的数学成绩是总体的一个样本.
A.1个
B.2个
C.3个
D.4个
8.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有( )
A.10人
B.12人
C.8人
D.9人
9.已知
a+b=3,ab=1,则a2+b2的值为( )
A.7
B.9
C.5
D.8
10.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,如图是公司为居民绘制的水费y(元)随当月用水量x(吨)变化而变化的图象,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家7月份缴水费30元,则该用户当月用水18.5吨
D.若小明家3月份用水14吨,则应缴水费23元
二、填空题(本大题满分15分,每小题3分,请你将答案填写在答题卡中)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是
.
12.如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2=
.
13.如图,小明从A地前往B地,到达后立刻返回,他与A地的距离y(千米)和所用时间x(小时)之间的关系如图所示,则小明出发5小时后距A地
千米.
14.计算:()2020×1.52021×(﹣1)2020=
.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第n个图形黑色棋子个数y与n的关系式为
.
三、解答题(本大题满分55分,解答要写出必要的文字说明或推演步骤)
16.计算:
(1)(π﹣3.14)0﹣+(﹣2)3;
(2)(3x+2)(2x﹣1).
17.先化简,再求值:
(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x),其中x=,y=2.
18.如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求:
(1)∠COD的度数;
(2)求∠MON的度数.
19.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表:
节目
人数(名)
百分比
最强大脑
a
10%
朗读者
15
b%
中国诗词大会
c
40%
出彩中国
10
20%
根据以上提供的信息,解答下列问题:
(1)x=
,a=
,b=
;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
20.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵
,
∴∠CDA=90°,∠DAB=90°(
).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴
(
),
∴DF∥AE(
).
21.某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,求A级所占百分比;
(2)在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数.
22.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
23.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
24.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
参考答案
一、选择题(本大题满分30分,每小题3分.每小题只有一个符合题意的选项,请你将正确选项的代号填在答题卡内)
1.下列四个选项中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
【分析】根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角可得答案.
解:根据同位角定义可得C中∠1,∠2是同位角,
故选:C.
2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000
0025米,把0.000
0025用科学记数法表示为( )
A.2.5×106
B.0.25×10﹣5
C.25×10﹣7
D.2.5×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000
0025=2.5×10﹣6,
故选:D.
3.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
【分析】点到直线的距离是指垂线段的长度.
解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
4.下列运算正确的是( )
A.3(a3)2=6a6
B.(a﹣2)(a﹣3)=a2﹣5a+6
C.x8÷x4=x2
D.3x3?2x2=6x6
【分析】根据整式的运算法则即可求出答案.
解:A、原式=3a6,故A错误.
C、原式=x4,故C错误,
D、原式=6x5,故D错误.
故选:B.
5.下列调查中,样本具有代表性的是( )
A.了解观众对所看电影的评价情况,对座位号是奇数的观众进行调查
B.了解全校同学对课程的喜欢情况,对某班男同学进行调查
C.了解商场的平均日营业额,选在周末进行调查
D.了解某小区居民的防火意识,对你们班同学进行调查
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
解:A、了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查,调查具有代表性、广泛性,故符合题意;
B、了解全校同学对课程的喜欢情况,对某班男同学进行调查,不具代表性、广泛性,故不符合题意;
C、了解商场的平均日营业额,选在周末进行调查,调查不具有代表性、广泛性,故不符合题意;
D、了解某小区居民的防火意识,对你们班同学进行调查,调查不具代表性、广泛性,故不符合题意;
故选:A.
6.如图,点C在线段AB上,AB=10cm,AC=4cm,点D是BC的中点,则BD=( )
A.2cm
B.3cm
C.5cm
D.6cm
【分析】根据已知条件先求出BC,再根据中点的性质求出BD即可.
解:∵AB=10cm,AC=4cm,
∴BC=AB﹣AC=6cm,
∵点D是BC的中点,
∴BD=BC=3cm.
故选:B.
7.某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计,下面判断中正确的有( )
①这种调查的方式是抽样调查;
②800名学生的数学成绩是总体;
③每名学生的期中数学成绩是个体;
④100名学生的数学成绩是总体的一个样本.
A.1个
B.2个
C.3个
D.4个
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体.本题考察的对象是我校八年级学生期中数学考试成绩,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
解:①很明显,这种调查方式是抽样调查.故正确;
②总体是七年级800名学生期中数学考试成绩.故错误;
③个体是七年级每个学生的期中数学考试成绩,这个说法正确.正确;
④100名学生的期中数学考试成绩才是总体的一个样本.故错误;
故正确的说法有①③共2个.
故选:B.
8.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有( )
A.10人
B.12人
C.8人
D.9人
【分析】根据A型血的有20人,所占的百分比是40%即可求得班级总人数,根据AB型所对应的扇形圆心角的度数求得对应的百分比,则用总人数乘以O型血所对应的百分比即可求解.
解:全班的人数是:20÷40%=50(人),
则O型血的人数是:50(1﹣40%﹣30%﹣10%)=10(人).
故选:A.
9.已知
a+b=3,ab=1,则a2+b2的值为( )
A.7
B.9
C.5
D.8
【分析】根据a2+b2=(a+b)2﹣2ab代入即可求解.
解:∵a+b=3,ab=1
∴a2+b2=(a+b)2﹣2ab
=32﹣2×1=7;
故选:A.
10.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,如图是公司为居民绘制的水费y(元)随当月用水量x(吨)变化而变化的图象,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家7月份缴水费30元,则该用户当月用水18.5吨
D.若小明家3月份用水14吨,则应缴水费23元
【分析】利用(10,15),(20,35)两点求出a,b的值即可.
解:由图象可知,a=15÷10=1.5;
b==2;
缴水费30元,则该用户当月用水为:10+(30﹣15)÷2=17.5(吨);
用水14吨,则应缴水费:1.5×10+2×(14﹣10)=15+8=23(元).
故结论错误的是选项C.
故选:C.
二、填空题(本大题满分15分,每小题3分,请你将答案填写在答题卡中)
11.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 t .
【分析】根据函数的定义:设x和y是两个变量,对于x的每一个值,y都有唯一确定的值和它对应,我们就说y是x的函数,其中x是自变量.据此解答即可.
解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
12.如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=35°,则∠2= 55° .
【分析】根据平角的定义求出∠3,再根据两直线平行,同位角相等可得∠2=∠3.
解:如图,∵∠1=35°,
∴∠3=180°﹣35°﹣90°=55°,
∵a∥b,
∴∠2=∠3=55°.
故答案为:55°.
13.如图,小明从A地前往B地,到达后立刻返回,他与A地的距离y(千米)和所用时间x(小时)之间的关系如图所示,则小明出发5小时后距A地
200 千米.
【分析】根据函数图象中的数据可以求得当4≤x≤10时,y与x的函数关系式,然后将x=5代入求得函数解析式,即可解答本题.
解:设当4≤x≤10时,y与x的函数关系式为y=kx+b,
则,
解得:
∴当4≤x≤10时,y与x的函数关系式为y=﹣40x+400,
∴当x=5时,y=﹣40×5+400=200,
即小明出发5小时后距A地200千米,
故答案为:200.
14.计算:()2020×1.52021×(﹣1)2020= .
【分析】逆向运用积的乘方运算法则以及有理数的乘方的定义计算即可.
解:()2020×1.52021×(﹣1)2020
=
=
=
=.
故答案为:.
15.用同样大小的黑色棋子按如图所示的规律摆放,则第n个图形黑色棋子个数y与n的关系式为
y=3n+3 .
【分析】根据图中所给的黑色棋子的颗数,找出其中的规律,用含n的代数式表示即可求出答案.
解:第1个图形有6颗黑色棋子,
第2个图形有9颗黑色棋子,
第3个图形有12颗黑色棋子,
第4个图形有15颗黑色棋子,
第5个图形有18颗黑色棋子,
?
第n个图形有棋子个数y=6+3(n﹣1)=3n+3,
故答案为:y=3n+3.
三、解答题(本大题满分55分,解答要写出必要的文字说明或推演步骤)
16.计算:
(1)(π﹣3.14)0﹣+(﹣2)3;
(2)(3x+2)(2x﹣1).
【分析】(1)根据零指数幂的性质,负整数指数幂的性质,乘方的定义分别求解各项的值,再合并即可求解;
(2)根据多项式乘多项式的运算法则计算可求解.
解:(1)原式=1﹣9﹣8
=﹣16;
(2)原式=6x2﹣3x+4x﹣2
=6x2+x﹣2.
17.先化简,再求值:
(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x),其中x=,y=2.
【分析】先根据整式的乘法法则和乘法公式算乘法,再合并同类项,最后代入求出即可.
解:(x+2y)(x﹣2y)+(x+2y)2﹣x(2y﹣x)
=x2﹣4y2+x2+4xy+4y2﹣2xy+x2
=3x2+2xy,
当x=,y=2时,原式3×()2+2××2=2.
18.如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求:
(1)∠COD的度数;
(2)求∠MON的度数.
【分析】(1)根据∠COD=∠AOB﹣∠AOC﹣∠BOD,代入即可求解;
(2)先根据角平分线的意义求出∠COM和∠DON,再根据∠MON=∠COM+∠DON+∠COD,即可求解.
解:(1)因为∠AOC=30°,∠BOD=60°,
所以∠COD═∠AOB﹣∠AOC﹣∠BOD=180°﹣30°﹣60°=90°
(3)因所OM,ON分别平分∠AOC,∠BOD
所以∠COM=15°,
∠DON=30°,
所以∠NOM=∠COM+∠DON+∠COD=15°+30°+90°=135°.
19.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表:
节目
人数(名)
百分比
最强大脑
a
10%
朗读者
15
b%
中国诗词大会
c
40%
出彩中国
10
20%
根据以上提供的信息,解答下列问题:
(1)x= 50 ,a= 5 ,b= 30 ;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
【分析】(1)根据喜爱出彩中国的人数和所占的百分比可以求得x的值,然后根据统计表中的数据,即可得到a和b的值;
(2)根据(1)中的结果可以得到c的值,从而可以将条形统计图补充完整;
(3)根据统计表中的数据,可以计算出该校最喜爱《中国诗词大会》节目的学生有多少名.
解:(1)x=10÷20%=50,
a=50×10%=5,
b%=15÷50×100%=30%,
故答案为:50,5,30;
(2)c=50×40%=20,
补全的条形统计图如右图所示;
(3)5000×40%=2000(名),
答:该校最喜爱《中国诗词大会》节目的学生有2000名.
20.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ CD⊥DA,DA⊥AB, ,
∴∠CDA=90°,∠DAB=90°(
垂直定义 ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ∠3=∠4 (
等角的余角相等 ),
∴DF∥AE(
内错角相等,两直线平行 ).
【分析】先根据垂直的定义,得到∠1+∠3=90°,∠2+∠4=90°,再根据等角的余角相等,得出∠3=∠4,最后根据内错角相等,两直线平行进行判定即可.
【解答】证明:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°,(垂直定义)
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴∠3=∠4,(等角的余角相等)
∴DF∥AE.(内错角相等,两直线平行)
故答案为:CD⊥DA,DA⊥AB,垂直定义,∠3=∠4,等角的余角相等,内错角相等,两直线平行.
21.某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,求A级所占百分比;
(2)在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数.
【分析】(1)根据A级对应的圆心角的度数可以求得A级所占百分比;
(2)根据A级对应的圆心角的度数和对应的频数,可以求得本次调查的总人数,然后即可求得D级的人数,从而可以将频数分布直方图补充完整;
(3)根据频数分布直方图中的数据,可以计算出D级对应的圆心角的度数,
解:(1)∵A级所在扇形的圆心角的度数为90°,
∴A级所占百分比为;
(2)∵A级有25人,占25%,
∴抽查的总人数为25÷25%=100(人),
∴D级有100﹣20﹣40﹣25=15(人),
补全的频数分布图如右图所示;
(3)D级的圆心角为:,
即D级对应的圆心角的度数为54°.
22.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,求∠AEF的度数.
【分析】根据平行线的性质和角平分线的定义解答即可.
解:∵AB∥CD,∠FGB=154°,
∴∠GFD=180°﹣∠FGB=180°﹣154°=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=2×26°=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
23.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)根据上表的数据,请你写出Q与t的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)该品牌汽车的油箱加50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
【分析】(1)由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少6L,据此可得t与Q的关系式;
(2)求汽车行驶5h后,油箱中的剩余油量即是求当t=5时,Q的值;
(3)贮满50L汽油的汽车,理论上最多能行驶几小时即是求当Q=50时,t的值.
解:(1)Q=100﹣6t;
(2)当t=5时,Q=100﹣6×5=70.
答:汽车行驶5h后,油箱中的剩余油量是70L;
(3)当Q=50时,50=100﹣6t,
6t=50,
解得:t=,
100×=km.
答:该车最多能行驶km.
24.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 兔子 (填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是 1500 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
【分析】(1)利用乌龟始终运动,中间没有停留,而兔子中间有休息的时刻,即可得出折线OABC的意义和全程的距离;
(2)根据图象中点A、D实际意义可得速度;
(3)根据乌龟的速度及兔子睡觉时的路程即可得;
(4)利用兔子的速度,求出兔子走完全程的时间,再求解即可.
解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
由图象可知:赛跑的全过程为1500米;
故答案为:兔子,1500;
(2)结合图象得出:
兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
(3)700÷30=(分钟),
所以乌龟用了分钟追上了正在睡觉的兔子.
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).
所以兔子中间停下睡觉用了46.5分钟.
同课章节目录
