2021-2022学年度鲁教版七年级上册数学全册课时随堂训练试题汇编(60页 Word版含答案)
文档属性
| 名称 | 2021-2022学年度鲁教版七年级上册数学全册课时随堂训练试题汇编(60页 Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览




文档简介
2022七年级上鲁教版五四数学随堂训练试题汇编
第一章 三角形
1 认识三角形
第1课时 三角形及其内角和
1.如图所示,图中三角形的个数为( )
第1题图
A.3
B.4
C.5
D.6
2.如图所示中x的值为( )
第2题图
A.40°
B.20°
C.30°
D.140°
3.如图所示,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )
第3题图
A.20°
B.30°
C.40°
D.50°
4.在△ABC中,∠A=60°,∠B比∠A小15°,则∠C的度数为 .?
5.如图所示,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的度数为 .?
6.(2021东平江河国际实验学校月考)在△ABC中,∠B-∠A=50°,
∠C-∠B=35°,求△ABC的各角的度数.
第2课时 三角形的分类及直角三角形的性质
1.下列说法中正确的是( )
A.三角形的内角中至少有两个锐角
B.三角形的内角中至少有两个钝角
C.三角形的内角中至少有一个直角
D.三角形的内角中至少有一个钝角
2.(2021威海文登二中检测)已知△ABC的三边长分别为a,b,c,且满足(a-2)2+|b-2|+|c-2|=0,则此三角形一定是( )
A.等边三角形
B.直角三角形
C.等腰直角三角形
D.一般三角形
3.(2021威海文登二中检测)在△ABC中,∠A=∠B=∠C,则这个三角形是( )
A.锐角三角形
B.等腰三角形
C.钝角三角形
D.含30°角的直角三角形
4.在一个直角三角形中,有一个锐角等于35°,则另一个锐角的度数是 .?
5.如图所示,在Rt△ABC中,∠C=90°,∠B=55°,点E为AC上一点,ED⊥AB,垂足为点D.求∠AED的度数.
第3课时 三角形的三边关系
1.(2021泰安东平实验中学期中)下列能组成三角形的线段是( )
A.3
cm,2
cm,6
cm
B.4
cm,7
cm,5
cm
C.2
cm,4
cm,6
cm
D.3
cm,6
cm,9
cm
2.(2020威海乳山期末)若三角形的两边长分别为6
cm,9
cm,则其第三边的长可能为( )
A.2
cm
B.3
cm
C.7
cm
D.16
cm
3.现有两根木棒分别长40
cm和50
cm,要从长度①5
cm;②10
cm;③40
cm;④45
cm;⑤80
cm;⑥90
cm的木棒中选出一根,与前面两根木棒钉成一个三角架(木棒不能余),则可选出( )
A.3条
B.4条
C.5条
D.6条
4.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c的值为 .?
5.有3
cm,6
cm,8
cm,9
cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形 个.?
6.用一条长为20
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是5
cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
第4课时 三角形中的三条重要线段
1.(2021威海文登二中检测)下面四个图形中,线段BE是△ABC的高的图是( )
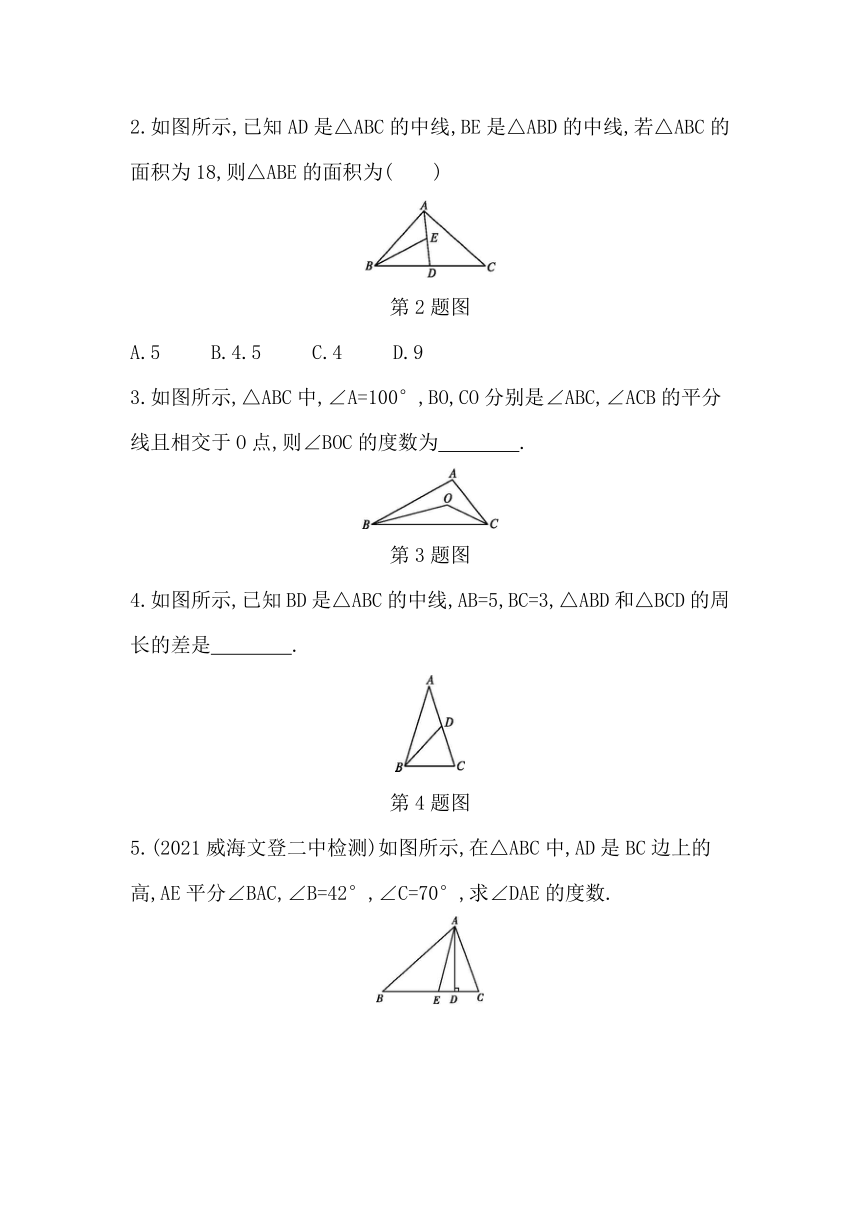
2.如图所示,已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )
第2题图
A.5
B.4.5
C.4
D.9
3.如图所示,△ABC中,∠A=100°,BO,CO分别是∠ABC,∠ACB的平分线且相交于O点,则∠BOC的度数为 .?
第3题图
4.如图所示,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .?
第4题图
5.(2021威海文登二中检测)如图所示,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=42°,∠C=70°,求∠DAE的度数.
2 图形的全等
1.下列图形中,两个图形全等的是( )
2.下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
3.(2021威海文登二中检测)如图所示,两个三角形是全等三角形,则x的值是 .?
第3题图
4.如图所示,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 .?
第4题图
5.如图所示,已知△ABC≌△DEF,∠B=∠E=90°,∠A=68°,AB=5,
BC=9,CF=6.
(1)求∠D,∠DFE的度数;
(2)求线段DE,CE的长.
3 探索三角形全等的条件
第1课时 边边边
1.如图所示,工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据为( )
第1题图
A.两点之间线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
2.如图所示,若AB=AC,DB=DC,∠B=85°,∠CDA=55°,则∠C的度数为( )
第2题图
A.40°
B.50°
C.85°
D.无法确定
3.如图所示,已知点A,D,B,F在一条直线上,AC=EF,BC=DE,要利用“SSS”判定△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)?
第3题图
4.如图所示,AB=DF,AC=DE,BE=FC,问:△ABC与△DEF全等吗?AB与DF平行吗?请说明你的理由.
第2课时 角边角或角角边
1.如图所示,小明不慎把一块三角形玻璃打碎成三块,现在他要去玻璃店配一块形状和原来完全一样的玻璃,要带以下玻璃去配,那么最简单的办法是带( )
第1题图
A.①
B.②
C.③
D.①②
2.(2020泰安泰山期末)如图所示,BC∥EF,AC∥DF,添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
第2题图
A.BC=EF
B.AC=DF
C.AD=BE
D.∠C=∠F
3.(2020威海乳山期末)如图所示,AB=AC,要使△ABE≌△ACD,应添加的条件是 .?
第3题图
4.如图所示,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是AE=1,CF=2,求EF长的值.
第3课时 边角边
1.如图所示,图中全等的三角形是( )
A.①和②
B.①和③
C.②和③
D.②和④
2.(2021泰安东平实验中学期中)在△ABC和△A′B′C′中有①AB=
A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥
∠C=∠C′,则下列各组条件中不能保证△ABC≌△A′B′C′的是( )
A.①②③
B.①②⑤
C.①②④
D.②⑤⑥
3.(2020泰安泰山期末)如图所示,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠AFC=∠AFE;②BF=DE;③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是 (填写所有正确结论的序号).?
4.如图所示,已知AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
4 三角形的尺规作图
1.如图所示,小敏做一道数学试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
2.已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m.下面作法:①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.合理顺序为 (填序号).?
3.(2021泰安东平实验中学期中)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α,直线l及l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
5 利用三角形全等测距离
1.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知小杨树高3
m,则塔松高( )
第1题图
A.大于3
m
B.等于3
m
C.小于3
m
D.和影子的长相同
2.(2021泰安东平实验中学期中)如图所示,把两根钢条A′B,AB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5
m,则槽宽为( )
第2题图
A.3
m
B.4
m
C.5
m
D.6
m
3.如图所示,高速公路上有A,B两点,在公路的同侧有C,D两村庄,已知DA=10
km,CB=15
km.DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,若C,D两村庄到服务站E的距离相等,且DE⊥EC,则AE的长是 km.?
第3题图
4.如图所示,在湖的两岸A,B间建一座观赏桥,由于条件限制,无法直接度量A,B两点间的距离.请你用学过的数学知识按以下要求设计一测量方案.
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示).
第二章 轴对称
1 轴对称现象
1.(2020泰安泰山期末)下列图形中,不是轴对称图形的是( )
2.如图所示,在下列四个图形,其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1
B.2
C.3
D.4
3.(2020泰安泰山期末)等边三角形的对称轴共有 条.?
4.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 .?
5.如图所示,在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连);
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
2 探索轴对称的性质
1.(2021东平江河国际实验学校月考)如图所示,若△ABC与
△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
第1题图
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
2.如图所示,△ABD和△ACD关于直线AD成轴对称,若BC=6,AD=5,则阴影部分的面积为 .?
第2题图
3.“又是一年三月三,风筝飞满天.”如图所示是一个燕子形风筝的图案,已知它是轴对称图形,对称轴为AF,则∠AFC的度数为 ,CF与CD的数量关系为 .?
第3题图
4.如图所示,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6
cm,BC=8
cm,试求△ACD的周长;
(2)如果∠CAD∶∠BAD=1∶2,求∠B的度数.
3 简单的轴对称图形
第1课时 线段垂直平分线的性质
1.已知点P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于( )
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.(2021泰安东平实验中学期中)如图所示,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点B)和图书馆(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A,点B和点C的距离相等,则装修物资应该放置在( )
A.AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在∠A,∠B两内角平分线的交点处
D.在AC,BC两边垂直平分线的交点处
3.(2021东营市垦利期中)如图所示,在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .?
4.如图所示,直线CP是AB的垂直平分线且交AB于点P,某人想在AB上取两点D,E,使得AD=DC,CE=EB,说明他应该如何做,并画出图形.
5.如图所示,A,B,C三点表示三个工厂,要建立一个供水站,使它到这三个工厂的距离相等,求作供水站的位置.(不写作法,尺规作图)
第2课时 角平分线的性质
1.(2021泰安东平实验中学期中)在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
第1题图
A.点M
B.点N
C.点P
D.点Q
2.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
第2题图
A.PA=PB
B.PO平分∠APB
C.AB垂直平分OP
D.OA=OB
3.如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=9
cm,则△DEB的周长是( )
第3题图
A.6
cm
B.7
cm
C.8
cm
D.9
cm
4.如图所示,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为点A,交CD于点D,若AD=8,则点P到BC的距离是 .?
第4题图
第3课时 等腰三角形的性质与判定
1.如图所示,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE的度数为( )
第1题图
A.15°
B.30°
C.45°
D.60°
2.(2021东平江河国际实验学校月考)等腰三角形的周长为18
cm,其中一条边为4
cm,那么等腰三角形的底边长为 .?
3.(2020泰安泰山期末)如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则∠ADB的度数是 .?
第3题图
4.(2020泰安泰山期末)如图所示,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q.试判断△APQ的形状,并证明你的结论.
4 利用轴对称进行设计
1.如图所示,将一张正方形纸片按如图所示方法折叠,再将图按虚线剪裁,将剪裁后的图展开后得到的图案是( )
2.如图所示,正方形硬纸片ABCD的边长是4,点E,F分别是AB,BC的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是 .?
3.如图所示,图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
1.直角三角形两直角边长分别为3和4,则它斜边上的高为( )
A.
B.7
C.5
D.
2.(2020高青期末)已知等腰三角形的一条腰长是15,底边长是18,则它底边上的高为( )
A.9
B.12
C.15
D.18
3.已知一个直角三角形的面积为84
cm2,其中一条直角边的长为7
cm,则该直角三角形的斜边的长为 cm.?
4.(2020烟台招远期中)如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10
cm,正方形A2的边长为6
cm,正方形B的边长为5
cm,正方形C的边长为5
cm,则正方形D的面积是 cm2.?
5.有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
第2课时 勾股定理的验证与应用
1.(2021泰安东平实验中学期中)如图所示,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4
000
m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3
000
m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
第1题图
A.2
000
m
B.3
000
m
C.4
000
m
D.5
000
m
2.(2020海淀校级期末)在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1
m,若将绳子拉直,绳端离旗杆底端的距离(BC)有5
m,则旗杆的高度为 m.?
第2题图
3.(2021河口实验期中)用四个全等的直角三角形拼成如图所示一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的世界数学家大会就用这个弦图作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .?
第3题图
2 一定是直角三角形吗
1.(2021泰安东平实验中学期中)在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,在下列条件中:①a=5,b=12,c=13;②∠A∶∠B∶∠C=3∶4∶5;③∠A-∠B=∠C;④a∶b∶c=1∶2∶3;⑤(b+c)(b-c)=a2,能判断
△ABC是直角三角形的有( )
A.1个
B.2个
C.3个
D.4个
2.(2021泰安东平实验中学期中)下列说法:
①若a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是3,4,那么斜边必是5;
③如果一个三角形的三边是12,25,21,那么此三角形必是直角三
角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2∶b2∶c2=2∶1∶1,其中正确的是( )
A.①②
B.①③
C.①④
D.②④
3.下列各组数:①1,2,3;②6,8,10;③0.3,0.4,0.5;④9,40,41;其中是勾股数的有 (填序号).?
4.若线段a,b,c满足b2=a2-c2,则以a,b,c为边的三角形是 三角形.?
5.观察下列各组勾股数,①4,3,5;②6,8,10;③8,15,17;④10,24,
26,…,寻找规律,请根据你发现的规律写出第⑦组勾股数是 .?
6.(2020高青期末)如图所示,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量AD=8
m,CD=6
m,∠ADC=90°,AB=
26
m,BC=24
m,若每平方草皮需要200元,则学校需要投入多少资金购买草皮?
3 勾股定理的应用举例
1.如图所示,有一个直角三角形纸片,直角边AC=6
cm,AB=10
cm,将
△ABC进行折叠使点B与点A重合,折痕为DE,那么CD长为
cm.?
第1题图
2.(2020莱州期末)如图所示是一个三级台阶,它的每一级的长、宽、高分别为100
cm,15
cm和10
cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为 .?
第2题图
3.(2020罗山期末)如图所示,在平静的湖面上,有一支红莲BA,高出水面的部分AC为1
m,一阵风吹来,红莲被吹到一边,花朵齐及水面(即AB=DB),已知红莲移动的水平距离CD为3
m,则湖水深CB为多少?
第四章 实数
1 无理数
1.(2020泰安泰山期末)下列四个实数中,是无理数的是( )
A.2.
B.3.14
C.
D.-π
2.(2020胜利一中期末)在实数0.23,4.,π,,0.303
003
000
3…(每两个3之间依次增加1个0)中,无理数有( )
A.1个
B.2个
C.3个
D.4个
3.下列语句正确的是( )
A.3.787
887
888
788
88是无理数
B.无理数分正无理数、零、负无理数
C.无限小数不能化成分数
D.无限不循环小数是无理数
4.-1到0之间的无理数有 个.?
5.把下列各数分别填入相应的集合里.
-5,-2.626
626
662…,0,π,-74,0.12,|-6|.
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
2 平方根
第1课时 算术平方根
1.下列各式中无意义的是( )
A.
B.
C.
D.
2.的值等于( )
A.
B.-
C.±
D.
3.(2020泰安泰山期末)的算术平方根的倒数是( )
A.4
B.
C.2
D.
4.有一个数值转换器,原理如图所示,当输入的数为16时,输出的数为 .?
5.(2020临淄期末)已知a,b满足(a-1)2+=0,则ab= .?
6.计算:
(1) (2) (3)
(4)
(5)
第2课时 平方根
1.(2020垦利期末)16的平方根是( )
A.±4
B.±2
C.4
D.-4
2.(2021泰安东平实验中学月考)下列语句正确的是( )
A.27的平方根是3
B.-9是-81的平方根
C.15是225的平方根
D.(-8)2的算术平方根是64
3.(2020莱州期末)的平方根是( )
A.±
B.
C.±
D.
4.(2020泰安泰山期末)若4x2-25=0,则x= .?
5.(2020东营胜利一中期末)的平方根是 .?
6.若2m-4与3m-1是同一个数两个不同的平方根,求m的值.
3 立方根
1.-27的立方根是( )
A.-3
B.3
C.-9
D.9
2.(2020胜利一中期末)下列说法正确的是( )
A.9的算术平方根是3
B.(-3)2的平方根是-3
C.1的立方根是±1
D.-4的平方根是±2
3.(2020威海乳山期末)的平方根为( )
A.2
B.±2
C.
D.±
4.(2021泰安东平实验中学月考)的立方根是 .?
5.(2021泰安东平实验中学月考)-8的立方根与的平方根之和是 . ?
6.(2020高青期末)已知4a+1的平方根是±3,b-1的算术平方根为2.
(1)求a与b的值;
(2)求2a+b-1的立方根.
4 估算
1.若k<A.8
B.9
C.10
D.11
2.比较三个数-3,-π,-的大小,下列结论正确的是( )
A.-π>-3>-
B.->-3>-π
C.->-π>-3
D.-3>-π>-
3.(2020莱州期末)写出-和之间的所有整数 .?
4.若a是的整数部分,则a(a+6)= .?
5.(2020河口期末)已知m是的整数部分,n是的小数部分,则m+n= .?
6.已知a为的整数部分,b-1是400的算术平方根,求a+b的平
方根.
5 用计算器开方
1.(2020临淄期末)在计算器上依次按键,得到的结果是( )
A.8
B.-8
C.4
D.-4
2.(2020莱州期末)在计算器上依次按键,显示的结果为( )
A.-5
B.5
C.-25
D.25
3.用计算器计算:≈ .(精确到0.01)?
4.用计算器计算:+-≈ .(精确到0.01)?
5.用计算器比较:5,4,3的大小(用“<”连接)
.?
6.在,,,…,中无理数的个数是 .?
6 实数
第1课时 实数及其性质
1.下列各数中,是无理数的是( )
A.3.141
5
B.
C.
D.
2.在实数:,π,,,2π,,0.36,0.373
773
777
3…(相邻两个3之间7的个数逐次加1),-,中,无理数的个数为( )
A.4
B.5
C.6
D.7
3.-3的相反数是 ,绝对值是 .?
4.已知与互为相反数,则x的值为 .?
5.(2020胜利一中期末)如图所示,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以点O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为 .?
第2课时 实数的运算与大小比较
1.(2019泰安)在实数|-3.14|,-3,-,π中,最小的数是( )
A.-
B.-3
C.|-3.14|
D.π
2.文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A.5
B.6
C.7
D.8
3.比较大小: 0.5.?
4.|-2|--= .?
5.(1)计算:-;
(2)计算:|-5|-(-1)0++;
(3)求x的值:(x-2)2=9.
第五章 位置与坐标
1 确定位置
1.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排
B.第3组第1排
C.第2组第3排
D.第2组第2排
2.(2021泰安东平实验中学月考)下列数据不能确定物体位置的是( )
A.电影票5排8号
B.北偏东30°
C.希望路25号
D.东经118°,北纬40°
3.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为( )
A.同一排
B.前后在同一条直线上
C.中间隔六个人
D.前后隔六排
4.如图所示是某地区简图的一部分,图中“故宫”所在的区域表示为E7,那么“鼓楼”所在的区域可以表示为 .?
第4题图
5.如图所示,O对应的有序数对为(1,3),有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来为 .?
第5题图
2 平面直角坐标系
第1课时 平面直角坐标系
1.(2020泰安泰山期末)点P(m+3,m+1)在直角坐标系的y轴上,则点P的坐标为( )
A.(-2,0)
B.(3,0)
C.(0,3)
D.(0,-2)
2.(2020高青期末)在平面直角坐标系内,点P(x,x+5)的位置一定不在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如图所示,在平面直角坐标系中,点A的坐标是 .?
4.点P(3,-2)到y轴的距离为 个单位.?
5.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2)四个点.
(1)线段AB,CD有什么关系?
(2)顺次连接A,B,C,D四点组成的图形,你认为它像什么?
第2课时 建立恰当的平面直角坐标系
1.如图所示,若点E的坐标为(-2,2),点F的坐标为(-1,0),则点G的坐标为( )
第1题图
A.(2,1)
B.(-2,1)
C.(2,-1)
D.(2,3)
2.(2020胜利一中期末)甲和乙下棋,甲执白子,乙执黑子.如图所示,一共下了7枚棋子,棋盘中心黑子的位置用(-1,0)表示,其右下角黑子的位置用(0,-1)表示.甲将第4枚白子放入棋盘后,所有棋子构成一个轴对称图形.他放的位置是( )
第2题图
A.(-1,1)
B.(-2,1)
C.(1,-2)
D.(-1,-2)
3.如图所示,在△OAB中,OA=AB=5,点B(6,0),则点A的坐标是
. ?
第3题图
4.如图所示,已知点A的坐标为(-2,2),点B的坐标为(-1,-2),则点C的坐标是 .?
第4题图
5.(2021泰安东平实验中学月考)如图所示,△ABC在正方形网格中,每个小正方形的边长为1个单位长度.若A(0,3),按要求回答下列
问题.
(1)在图中建立恰当的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.
3 轴对称与坐标变化
1.在平面直角坐标系中,点A的坐标为(-2,3),点B的坐标为(-2,-3),那么点A和点B的位置关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.关于坐标轴和原点都不对称
2.(2020高青期末)已知点A(a-2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1
B.3
C.-1
D.5
3.已知点P1,P2关于x轴对称,点P2,P3关于y轴对称,点P3的坐标为(-3,4),则点P1的坐标为 .?
4.(2020胜利一中期末)已知点A(a-1,5)与点B(2,b-1)关于x轴对称,则(a+b)2
020= .?
5.已知等腰直角△ABC的斜边AB在x轴上,点C在y轴上,若点A的坐标是(-3,0),则点B的坐标为 .?
6.(2020垦利期末)如图所示,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点坐标分别为A(-4,1),B(-3,3),C(-1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1,B1,C1,写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,并求出△CC1C2的面积.
第六章 一次函数
1 函数
1.下列两个变量之间,不存在函数关系的是( )
A.一天的气温与时间之间的关系
B.一个正数的平方根与这个正数之间的关系
C.圆的面积与圆的周长之间的关系
D.速度一定,汽车行驶的路程与行驶时间之间的关系
2.(2020河口期末)如图所示,在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGD,动点P从点A出发,沿A→E→F→G→C→B的路线,绕多边形的边匀速运动到点B时停止,则△ABP的面积S随着时间t变化的函数图象大致是( )
3.某市的夏天经常刮台风,给人们的出行带来很多不便,小欣了解到该市去年8月16日连续12个小时的风力变化情况,并画出了风力随时间变化的图象(如图所示),则下列说法正确的是( )
A.8时风力最小
B.在8时至12时,风力最大为5级
C.在12时至14时,风力最大为7级
D.8时至14时,风力不断增大
4.公式L=L0+KP表示当重力为P的物体作用在弹簧上时弹簧的长度,L0代表弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
A.L=10+0.5P
B.L=10+5P
C.L=80+0.5P
D.L=80+5P
5.(2020垦利期末)小明从家沿笔直的公路骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,如图所示是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 m;?
(2)小明在书店停留了 min;?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
2 一次函数
1.下列函数中,是一次函数的有( )
①y=;②y=4x;③y=x;④y=+1;⑤y=2x2-1.
A.1个
B.2个
C.3个
D.4个
2.下列y关于x的函数中,是正比例函数的为( )
A.y=x2
B.y=
C.y=x
D.y=x+1
3.已知A,B两地相距30
km,小明以6
km/h的速度从A地步行到B地,记小明步行的距离为y
km,步行的时间为x
h.则y与x之间的函数表达式是
,y是x的
函数,自变量的取值范围是 .?
4.某水库的水位在5小时内持续上涨,初始的水位高度为6
m,水位以0.3
m/h
的速度匀速上升,则水库的水位高度y
m与时间x
h(0≤x≤5)的函数关系为 .?
5.当m,n为何值时,y=(m-1)+n.(注:指数为m2)
(1)是一次函数;
(2)是正比例函数.
3 一次函数的图象
第1课时 正比例函数的图象与性质
1.正比例函数y=kx的图象如图所示,则k的取值范围是( )
第1题图
A.k>0
B.k<0
C.k>1
D.k<1
2.关于正比例函数y=-3x,下列结论正确的是( )
A.图象不经过原点
B.y随x的增大而增大
C.图象经过第二、四象限
D.当x=时,y=1
3.经过以下一组点坐标可以画出函数y=2x图象的是( )
A.(0,0)和(2,1)
B.(1,2)和(-1,-2)
C.(1,2)和(2,1)
D.(-1,2)和(1,2)
4.已知正比例函数y=(k-2)x,若y随x的增大而增大,则k的取值范围是 .?
5.如图所示,三个正比例函数的图象对应的表达式分别为①y=ax,②y=bx,③y=cx,则a,b,c的大小关系是 .?
第5题图
6.已知正比例函数y=kx.
(1)若函数图象经过第二、四象限,则k的范围是什么?
(2)若点(1,-2)在它的图象上,求它的表达式.
第2课时 一次函数的图象与性质
1.(2020莱州期末)如图所示,表示一次函数的是( )
2.(2020河口期末)关于函数y=-2x+1,下列结论正确的是( )
A.图象经过点(-2,1)
B.y随x的增大而增大
C.图象不经过第三象限
D.图象不经过第二象限
3.(2020高青期末)已知点(k,b)为第二象限内的点,则一次函数y=-kx+b的图象大致是( )
4.(2020莱州期末)在平面直角坐标系中,已知一次函数y=kx-b(k<0)的图象经过P1(-1,y1),P2(2,y2)两点,则y1 y2(填“>”“=”或“<”).?
5.一次函数y=-3x-9的图象与x轴的交点坐标是 ,与y轴的交点坐标是 .?
6.已知,一次函数y=2x-4.
(1)在给定的直角坐标系中画出这个函数的图象;
(2)根据图象,说出函数的三条性质(或图象特征).
4 确定一次函数的表达式
1.已知一次函数y=kx-2,当x=2时,y=1,则k的值为( )
A.-
B.
C.
D.
2.如图所示,某正比例函数的图象过点M(-2,1),则此正比例函数的表达式为( )
第2题图
A.y=-x
B.y=x
C.y=-2x
D.y=2x
3.(2020胜利一中期末)如图所示,直线l是一次函数y=kx+b(k≠0)的图象,则b= .?
第3题图
4.(2020垦利期末)将一次函数y=2x-3的图象沿y轴向上平移5个单位后,得到的图象对应的函数表达式为 .?
5.在平面直角坐标系中,如果点(x,4),(0,8),(-4,0)在同一条直线上,则x= .?
6.一次函数的图象经过点A(3,7)和B(0,-2)两点.
(1)求出该一次函数的表达式;
(2)判断是否在这个函数的图象上.
5 一次函数的应用
1.一根蜡烛长30
cm,点燃后每小时燃烧5
cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(h)之间的函数关系用图象可以表示为( )
2.若一次函数y=kx+3(k为常数且k≠0)的图象经过点(-2,0),则关于x的方程k(x-5)+3=0的解为( )
A.x=-5
B.x=-3
C.x=3
D.x=5
3.如图所示是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:①买2件时甲、乙两家售价一样;②买1件时选乙家的产品合算;③买3件时选甲家的产品合算;④买1件时,售价约为3元.其中正确的说法是 (填写序号).?
4.(2020泰安泰山期末)某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费
200元.若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为
x
km,通过铁路运输和公路运输需交总运费y1元和y2元.
(1)求y1和y2关于x的表达式;
(2)若A地到B地的路程为120
km,哪种运输可以节省总运费?
参考答案
第一章 三角形
1 认识三角形
第1课时 三角形及其内角和
1.C 2.B 3.C 4.75° 5.14°
6.解:由三角形内角和定理,得∠A+∠B+∠C=180°,
则
解得∠A=15°,∠B=65°,∠C=100°.
第2课时 三角形的分类及直角
三角形的性质
1.A 2.A 3.D 4.55°
5.解:因为ED⊥AB,所以∠ADE=90°.因为∠C=90°,∠B=55°,所以
∠A=35°.所以∠AED=55°.
第3课时 三角形的三边关系
1.B 2.C 3.A 4.7 5.3
6.解:(1)设底边长为x
cm,则腰长为2x
cm.由题意,得2x+2x+x=20,解得x=4.
所以2x=8.
所以三角形三边的长分别为8
cm,8
cm,4
cm.
(2)若腰长为5
cm,则底边长为20-5-5=10
cm.
而5+5=10,所以不能围成腰长为5
cm的等腰三角形.
若底边长为5
cm,则腰长为×(20-5)=cm.此时能围成等腰三角形,三边长分别为5
cm,cm,cm.
第4课时 三角形中的
三条重要线段
1.D 2.B 3.140° 4.2
5.解:因为∠B=42°,∠C=70°,
所以∠BAC=180°-∠B-∠C=68°.
因为AE平分∠BAC,
所以∠CAE=∠BAC=34°.
因为AD是BC边上的高,
所以∠ADC=90°.
因为∠C=70°,
所以∠CAD=180°-∠ADC-∠C=20°.
所以∠DAE=∠CAE-∠CAD=34°-20°=14°.
2 图形的全等
1.B 2.B 3.30 4.70°
5.解:(1)因为△ABC≌△DEF,
所以∠D=∠A=68°,∠DFE=∠ACB=90°-68°=22°.
(2)因为△ABC≌△DEF,
所以DE=AB=5,
EF=BC=9.
所以CE=EF-CF=9-6=3.
3 探索三角形全等的条件
第1课时 边边边
1.D 2.C
3.AB=DF(或AD=BF答案不唯一)
4.解:全等;平行.理由如下:
因为BE=FC,
所以BE+CE=CE+CF.
所以BC=EF.
在△ABC和△DFE中,
所以△ABC≌△DFE(SSS).
所以∠B=∠F.
所以AB∥DF.
第2课时 角边角或角角边
1.C 2.D
3.∠B=∠C(答案不唯一)
4.解:因为四边形ABCD为正方形,
所以AB=BC,∠ABC=90°.
因为AE⊥BE,CF⊥BF,
所以∠AEB=∠BFC=90°.
所以∠EAB+∠ABE=90°,
∠ABE+∠FBC=90°.
所以∠EAB=∠FBC.
在△ABE和△BCF中,
所以△ABE≌△BCF.
所以BE=CF=2,
AE=BF=1.
所以EF=BE+BF=3.
第3课时 边角边
1.B 2.C 3.①③④
4.证明:因为∠BAE=∠DAC,
所以∠BAE-∠CAE
=∠DAC-∠CAE,
即∠BAC=∠DAE.
在△ABC和△ADE中,
因为AB=AD,
∠BAC=∠DAE,AC=AE,
所以△ABC≌△ADE(SAS).
所以∠C=∠E.
4 三角形的尺规作图
1.C 2.③①②
3.解:如图所示,△ABC为所作.
5 利用三角形全等测距离
1.B 2.C 3.15
4.解:(1)测量图案,如图所示.
(2)在湖岸上选一点O,连接BO并延长到C使OC=BO,连接AO并延长到点D使OD=AO,连接CD,则CD=AB.测量DC的长度即为AB的长度.
(3)设DC=m,因为BO=CO,∠AOB=∠DOC,AO=DO,根据SAS,
所以△AOB≌△DOC.
所以AB=CD=m.
第二章 轴对称
1 轴对称现象
1.D 2.C 3.3 4.书
5.解:如图所示,答案不唯一.
2 探索轴对称的性质
1.B 2.7.5 3.90° CF=CD
4.解:(1)由折叠的性质可知,DE垂直平分线段AB,
且DA=DB,
所以△ACD的周长为DA+DC+AC=DB+DC+AC=BC+AC=14
cm.
(2)设∠CAD=x,则∠BAD=2x,
因为DA=DB,
所以∠B=∠BAD=2x.
在Rt△ABC中,∠B+∠BAC=90°,
即2x+2x+x=90°,x=18°.
所以∠B=2x=36°.
3 简单的轴对称图形
第1课时 线段垂直平分线的性质
1.A 2.D 3.15
4.
解:如图所示,作AC,BC的
垂直平分线,分别交AB于点D,E,则点D,E即为所求.
5.解:如图所示,点P即为所求.
第2课时 角平分线的性质
1.A 2.C 3.D 4.4
第3课时 等腰三角形的
性质与判定
1.A 2.4
cm 3.108°
4.解:△APQ是等腰三角形.
证明:因为∠QDB=∠DQC+∠C,∠PDC=∠B+∠P,
又因为AB=AC,
所以∠B=∠C.
所以∠P=∠DQC=∠AQP.
所以AP=AQ.
所以△APQ是等腰三角形.
4 利用轴对称进行设计
1.B 2.4
3.解:如图所示:
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
1.A 2.B 3.25 4.14
5.解:在Rt△ABE中,
由勾股定理,得AE2=AB2+BE2=402+92=1
681.所以AE=41.而AB+BE=40+9=49,因为49-41=8,
所以标牌上填的数是8.
第2课时 勾股定理的验证与应用
1.D 2.12 3.4
2 一定是直角三角形吗
1.C 2.C 3.②④ 4.直角
5.16,63,65
6.解:如图所示,连接AC,
因为∠ADC=90°,在Rt△ACD中,由勾股定理,得AC2=AD2+CD2=82+62=100,所以AC=10
m.在△ABC中,AC2+BC2=102+242=100+576=676,AB2=262=676,所以AC2+BC2=AB2.所以△ABC是直角三角形,其中∠ACB=90°.所以四边形ABCD的面积为S=S△ABC-S△ACD=AC·BC-AD·CD=×10×24-×8×6=120-24=96(m2).96×200=19
200(元),所以学校需要投入资金19
200元购买草皮.
3 勾股定理的应用举例
1. 2.125
cm
3.解:设BC为h
m,
在Rt△BCD中,BC=h,BD=AB=h+1,DC=3,
由勾股定理,得BD2=DC2+BC2,即(h+1)2=h2+32,解得h=4.因此湖深BC为4
m.
第四章 实数
1 无理数
1.D 2.B 3.D 4.无数
5.解:(1)正数集合:{π,0.12,|-6|,…};
(2)负数集合:{-5,
-2.626
626
662…,-74,…};
(3)有理数集合:{-5,0,-74,0.12,|-6|,…};
(4)无理数集合:
{-2.626
626
662…,π,…}.
2 平方根
第1课时 算术平方根
1.B 2.A 3.D 4. 5.1
6.解:(1)=8.
(2)==2.
(3)=0.9.
(4)=.
(5)=10-2.
第2课时 平方根
1.A 2.C 3.C 4.± 5.±2
6.解:根据题意,得
(2m-4)+(3m-1)=0,
解得m=1.所以m的值为1.
3 立方根
1.A 2.A 3.D 4.2
5.1或-5
6.解:(1)因为4a+1的平方根是±3,所以4a+1=9,解得a=2.
因为b-1的算术平方根为2,
所以b-1=4,解得b=5.
(2)因为a=2,b=5,所以2a+b-1=2×2+5-1=8.因为=2,所以2a+b-1的立方根是2.
4 估算
1.B 2.B 3.-1,0,1 4.27 5.
6.解:因为的整数部分是4,即a=4,因为b-1==20,所以b=21.所以a+b=25.因为25的平方根是±5.即a+b的平方根是±5.
5 用计算器开方
1.C 2.A 3.16.15 4.0.91
5.3<4<5
6.1
966
6 实数
第1课时 实数及其性质
1.D 2.A 3.3- 3-
4.3 5.
第2课时 实数的运算与大小比较
1.B 2.B 3.> 4.3
5.解:(1)-=2-(-2)=4.
(2)原式=5-1+9-3=10.
(3)开方,得x-2=3,或x-2=-3,
解得x=5或x=-1.
第五章 位置与坐标
1 确定位置
1.C 2.B 3.A
4.D6 5.HELLO
2 平面直角坐标系
第1课时 平面直角坐标系
1.D 2.D 3.(-2,3)
4.3
5.解:描出A,B,C,D四个点,如图所示.
(1)由图,知AB∥CD,AB=CD.
(2)由A,B,C,D构成的图形像“Z”字.
第2课时 建立恰当的平面直
角坐标系
1.A 2.A 3.(3,4) 4.(2,1)
5.解:(1)建立平面直角坐标系如图所示.
(2)根据坐标系可得出B(-3,-1),C(1,1).
(3)S△ABC=4×4-×4×2-×3×4-×1×2=5.
3 轴对称与坐标变化
1.A 2.B 3.(3,-4) 4.1
5.(3,0)
6.解:(1)如图所示,△A1B1C1即为所求.
点A1,B1,C1的坐标分别为A1(-4,-1),B1(-3,-3),C1(-1,-2),
(2)如图所示,△CC1C2的面积是×2×4=4.
第六章 一次函数
1 函数
1.B 2.B 3.C 4.A
5.解:(1)根据图象,学校的纵坐标为1
500,小明家的纵坐标为0,
故小明家到学校的路程是1
500
m.
(2)根据题意,小明在书店停留的时间为从8
min到12
min,
故小明在书店停留了12-8=4(min).
(3)因为1
200+(1
200-600)+(1
500-600)=1
200+600+900=2
700(m),
所以小明一共行驶的总路程为2
700
m,共用了14
min.
2 一次函数
1.C 2.C
3.y=6x 正比例 0≤x≤5
4.y=6+0.3x
5.解:(1)当m2=1且m-1≠0时,y=(m-1)+n是一次函数,即m=-1.所以当m=-1,n为任意实数时,y=(m-1)+n是一次函数.
(2)当m2=1且m-1≠0,且n=0时,y=(m-1)+n是正比例函数,即m=-1且n=0,所以当m=-1且n=0时,y=(m-1)+n是正比例函数.
3 一次函数的图象
第1课时 正比例函数的
图象与性质
1.A 2.C 3.B 4.k>2
5.c>b>a
6.解:(1)因为函数图象经过第二、四象限,所以k<0.
(2)当x=1时,y=-2,
则k=-2,
即y=-2x.
第2课时 一次函数的图象与性质
1.B 2.C 3.C 4.>
5.(-3,0) (0,-9)
6.解:(1)令y=2x-4=0,解得x=2,
令x=0,解得y=-4,
所以一次函数与两坐标轴的交点坐标为(2,0)和(0,-4),所以图象如图所示.
(2)性质:y随x的增大而增大;
与两坐标轴围成的面积为4;
函数图象不经过第二象限.
4 确定一次函数的表达式
1.D 2.A 3.1
4.y=2x+2 5.-2
6.解:(1)设一次函数的表达式为
y=kx+b(k≠0),
根据题意,将A,B两点的坐标分别代入,得
解得
所以一次函数的表达式为y=3x-2.
(2)对于y=3x-2,
当x=时,
y=3×-2=-1,
所以点在一次函数y=3x-2的图象上.
5 一次函数的应用
1.B 2.C 3.①②③
4.解:(1)根据题意,得y1=
15x+400+200=15x+600;
y2=25x+100(x>0).
(2)当x=120时,
y1=15×120+600=2
400,
y2=25×120+100=3
100,
因为y1所以铁路运输节省总运费.
第一章 三角形
1 认识三角形
第1课时 三角形及其内角和
1.如图所示,图中三角形的个数为( )
第1题图
A.3
B.4
C.5
D.6
2.如图所示中x的值为( )
第2题图
A.40°
B.20°
C.30°
D.140°
3.如图所示,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )
第3题图
A.20°
B.30°
C.40°
D.50°
4.在△ABC中,∠A=60°,∠B比∠A小15°,则∠C的度数为 .?
5.如图所示,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的度数为 .?
6.(2021东平江河国际实验学校月考)在△ABC中,∠B-∠A=50°,
∠C-∠B=35°,求△ABC的各角的度数.
第2课时 三角形的分类及直角三角形的性质
1.下列说法中正确的是( )
A.三角形的内角中至少有两个锐角
B.三角形的内角中至少有两个钝角
C.三角形的内角中至少有一个直角
D.三角形的内角中至少有一个钝角
2.(2021威海文登二中检测)已知△ABC的三边长分别为a,b,c,且满足(a-2)2+|b-2|+|c-2|=0,则此三角形一定是( )
A.等边三角形
B.直角三角形
C.等腰直角三角形
D.一般三角形
3.(2021威海文登二中检测)在△ABC中,∠A=∠B=∠C,则这个三角形是( )
A.锐角三角形
B.等腰三角形
C.钝角三角形
D.含30°角的直角三角形
4.在一个直角三角形中,有一个锐角等于35°,则另一个锐角的度数是 .?
5.如图所示,在Rt△ABC中,∠C=90°,∠B=55°,点E为AC上一点,ED⊥AB,垂足为点D.求∠AED的度数.
第3课时 三角形的三边关系
1.(2021泰安东平实验中学期中)下列能组成三角形的线段是( )
A.3
cm,2
cm,6
cm
B.4
cm,7
cm,5
cm
C.2
cm,4
cm,6
cm
D.3
cm,6
cm,9
cm
2.(2020威海乳山期末)若三角形的两边长分别为6
cm,9
cm,则其第三边的长可能为( )
A.2
cm
B.3
cm
C.7
cm
D.16
cm
3.现有两根木棒分别长40
cm和50
cm,要从长度①5
cm;②10
cm;③40
cm;④45
cm;⑤80
cm;⑥90
cm的木棒中选出一根,与前面两根木棒钉成一个三角架(木棒不能余),则可选出( )
A.3条
B.4条
C.5条
D.6条
4.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c的值为 .?
5.有3
cm,6
cm,8
cm,9
cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形 个.?
6.用一条长为20
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是5
cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
第4课时 三角形中的三条重要线段
1.(2021威海文登二中检测)下面四个图形中,线段BE是△ABC的高的图是( )
2.如图所示,已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )
第2题图
A.5
B.4.5
C.4
D.9
3.如图所示,△ABC中,∠A=100°,BO,CO分别是∠ABC,∠ACB的平分线且相交于O点,则∠BOC的度数为 .?
第3题图
4.如图所示,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .?
第4题图
5.(2021威海文登二中检测)如图所示,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=42°,∠C=70°,求∠DAE的度数.
2 图形的全等
1.下列图形中,两个图形全等的是( )
2.下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
3.(2021威海文登二中检测)如图所示,两个三角形是全等三角形,则x的值是 .?
第3题图
4.如图所示,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 .?
第4题图
5.如图所示,已知△ABC≌△DEF,∠B=∠E=90°,∠A=68°,AB=5,
BC=9,CF=6.
(1)求∠D,∠DFE的度数;
(2)求线段DE,CE的长.
3 探索三角形全等的条件
第1课时 边边边
1.如图所示,工人师傅砌门常用木条EF固定长方形门框ABCD,使其不变形的根据为( )
第1题图
A.两点之间线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
2.如图所示,若AB=AC,DB=DC,∠B=85°,∠CDA=55°,则∠C的度数为( )
第2题图
A.40°
B.50°
C.85°
D.无法确定
3.如图所示,已知点A,D,B,F在一条直线上,AC=EF,BC=DE,要利用“SSS”判定△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)?
第3题图
4.如图所示,AB=DF,AC=DE,BE=FC,问:△ABC与△DEF全等吗?AB与DF平行吗?请说明你的理由.
第2课时 角边角或角角边
1.如图所示,小明不慎把一块三角形玻璃打碎成三块,现在他要去玻璃店配一块形状和原来完全一样的玻璃,要带以下玻璃去配,那么最简单的办法是带( )
第1题图
A.①
B.②
C.③
D.①②
2.(2020泰安泰山期末)如图所示,BC∥EF,AC∥DF,添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
第2题图
A.BC=EF
B.AC=DF
C.AD=BE
D.∠C=∠F
3.(2020威海乳山期末)如图所示,AB=AC,要使△ABE≌△ACD,应添加的条件是 .?
第3题图
4.如图所示,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是AE=1,CF=2,求EF长的值.
第3课时 边角边
1.如图所示,图中全等的三角形是( )
A.①和②
B.①和③
C.②和③
D.②和④
2.(2021泰安东平实验中学期中)在△ABC和△A′B′C′中有①AB=
A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥
∠C=∠C′,则下列各组条件中不能保证△ABC≌△A′B′C′的是( )
A.①②③
B.①②⑤
C.①②④
D.②⑤⑥
3.(2020泰安泰山期末)如图所示,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠AFC=∠AFE;②BF=DE;③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是 (填写所有正确结论的序号).?
4.如图所示,已知AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
4 三角形的尺规作图
1.如图所示,小敏做一道数学试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
2.已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m.下面作法:①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.合理顺序为 (填序号).?
3.(2021泰安东平实验中学期中)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α,直线l及l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
5 利用三角形全等测距离
1.如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知小杨树高3
m,则塔松高( )
第1题图
A.大于3
m
B.等于3
m
C.小于3
m
D.和影子的长相同
2.(2021泰安东平实验中学期中)如图所示,把两根钢条A′B,AB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得AB=5
m,则槽宽为( )
第2题图
A.3
m
B.4
m
C.5
m
D.6
m
3.如图所示,高速公路上有A,B两点,在公路的同侧有C,D两村庄,已知DA=10
km,CB=15
km.DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,若C,D两村庄到服务站E的距离相等,且DE⊥EC,则AE的长是 km.?
第3题图
4.如图所示,在湖的两岸A,B间建一座观赏桥,由于条件限制,无法直接度量A,B两点间的距离.请你用学过的数学知识按以下要求设计一测量方案.
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示).
第二章 轴对称
1 轴对称现象
1.(2020泰安泰山期末)下列图形中,不是轴对称图形的是( )
2.如图所示,在下列四个图形,其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1
B.2
C.3
D.4
3.(2020泰安泰山期末)等边三角形的对称轴共有 条.?
4.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 .?
5.如图所示,在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)要求:
(1)5个小正方形必须相连(有公共边或公共顶点视为相连);
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)
2 探索轴对称的性质
1.(2021东平江河国际实验学校月考)如图所示,若△ABC与
△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
第1题图
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
2.如图所示,△ABD和△ACD关于直线AD成轴对称,若BC=6,AD=5,则阴影部分的面积为 .?
第2题图
3.“又是一年三月三,风筝飞满天.”如图所示是一个燕子形风筝的图案,已知它是轴对称图形,对称轴为AF,则∠AFC的度数为 ,CF与CD的数量关系为 .?
第3题图
4.如图所示,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6
cm,BC=8
cm,试求△ACD的周长;
(2)如果∠CAD∶∠BAD=1∶2,求∠B的度数.
3 简单的轴对称图形
第1课时 线段垂直平分线的性质
1.已知点P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于( )
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.(2021泰安东平实验中学期中)如图所示,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点B)和图书馆(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A,点B和点C的距离相等,则装修物资应该放置在( )
A.AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在∠A,∠B两内角平分线的交点处
D.在AC,BC两边垂直平分线的交点处
3.(2021东营市垦利期中)如图所示,在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .?
4.如图所示,直线CP是AB的垂直平分线且交AB于点P,某人想在AB上取两点D,E,使得AD=DC,CE=EB,说明他应该如何做,并画出图形.
5.如图所示,A,B,C三点表示三个工厂,要建立一个供水站,使它到这三个工厂的距离相等,求作供水站的位置.(不写作法,尺规作图)
第2课时 角平分线的性质
1.(2021泰安东平实验中学期中)在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
第1题图
A.点M
B.点N
C.点P
D.点Q
2.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
第2题图
A.PA=PB
B.PO平分∠APB
C.AB垂直平分OP
D.OA=OB
3.如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=9
cm,则△DEB的周长是( )
第3题图
A.6
cm
B.7
cm
C.8
cm
D.9
cm
4.如图所示,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为点A,交CD于点D,若AD=8,则点P到BC的距离是 .?
第4题图
第3课时 等腰三角形的性质与判定
1.如图所示,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE的度数为( )
第1题图
A.15°
B.30°
C.45°
D.60°
2.(2021东平江河国际实验学校月考)等腰三角形的周长为18
cm,其中一条边为4
cm,那么等腰三角形的底边长为 .?
3.(2020泰安泰山期末)如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则∠ADB的度数是 .?
第3题图
4.(2020泰安泰山期末)如图所示,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q.试判断△APQ的形状,并证明你的结论.
4 利用轴对称进行设计
1.如图所示,将一张正方形纸片按如图所示方法折叠,再将图按虚线剪裁,将剪裁后的图展开后得到的图案是( )
2.如图所示,正方形硬纸片ABCD的边长是4,点E,F分别是AB,BC的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是 .?
3.如图所示,图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
1.直角三角形两直角边长分别为3和4,则它斜边上的高为( )
A.
B.7
C.5
D.
2.(2020高青期末)已知等腰三角形的一条腰长是15,底边长是18,则它底边上的高为( )
A.9
B.12
C.15
D.18
3.已知一个直角三角形的面积为84
cm2,其中一条直角边的长为7
cm,则该直角三角形的斜边的长为 cm.?
4.(2020烟台招远期中)如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10
cm,正方形A2的边长为6
cm,正方形B的边长为5
cm,正方形C的边长为5
cm,则正方形D的面积是 cm2.?
5.有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
第2课时 勾股定理的验证与应用
1.(2021泰安东平实验中学期中)如图所示,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4
000
m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3
000
m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为( )
第1题图
A.2
000
m
B.3
000
m
C.4
000
m
D.5
000
m
2.(2020海淀校级期末)在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1
m,若将绳子拉直,绳端离旗杆底端的距离(BC)有5
m,则旗杆的高度为 m.?
第2题图
3.(2021河口实验期中)用四个全等的直角三角形拼成如图所示一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的世界数学家大会就用这个弦图作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .?
第3题图
2 一定是直角三角形吗
1.(2021泰安东平实验中学期中)在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,在下列条件中:①a=5,b=12,c=13;②∠A∶∠B∶∠C=3∶4∶5;③∠A-∠B=∠C;④a∶b∶c=1∶2∶3;⑤(b+c)(b-c)=a2,能判断
△ABC是直角三角形的有( )
A.1个
B.2个
C.3个
D.4个
2.(2021泰安东平实验中学期中)下列说法:
①若a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是3,4,那么斜边必是5;
③如果一个三角形的三边是12,25,21,那么此三角形必是直角三
角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2∶b2∶c2=2∶1∶1,其中正确的是( )
A.①②
B.①③
C.①④
D.②④
3.下列各组数:①1,2,3;②6,8,10;③0.3,0.4,0.5;④9,40,41;其中是勾股数的有 (填序号).?
4.若线段a,b,c满足b2=a2-c2,则以a,b,c为边的三角形是 三角形.?
5.观察下列各组勾股数,①4,3,5;②6,8,10;③8,15,17;④10,24,
26,…,寻找规律,请根据你发现的规律写出第⑦组勾股数是 .?
6.(2020高青期末)如图所示,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量AD=8
m,CD=6
m,∠ADC=90°,AB=
26
m,BC=24
m,若每平方草皮需要200元,则学校需要投入多少资金购买草皮?
3 勾股定理的应用举例
1.如图所示,有一个直角三角形纸片,直角边AC=6
cm,AB=10
cm,将
△ABC进行折叠使点B与点A重合,折痕为DE,那么CD长为
cm.?
第1题图
2.(2020莱州期末)如图所示是一个三级台阶,它的每一级的长、宽、高分别为100
cm,15
cm和10
cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为 .?
第2题图
3.(2020罗山期末)如图所示,在平静的湖面上,有一支红莲BA,高出水面的部分AC为1
m,一阵风吹来,红莲被吹到一边,花朵齐及水面(即AB=DB),已知红莲移动的水平距离CD为3
m,则湖水深CB为多少?
第四章 实数
1 无理数
1.(2020泰安泰山期末)下列四个实数中,是无理数的是( )
A.2.
B.3.14
C.
D.-π
2.(2020胜利一中期末)在实数0.23,4.,π,,0.303
003
000
3…(每两个3之间依次增加1个0)中,无理数有( )
A.1个
B.2个
C.3个
D.4个
3.下列语句正确的是( )
A.3.787
887
888
788
88是无理数
B.无理数分正无理数、零、负无理数
C.无限小数不能化成分数
D.无限不循环小数是无理数
4.-1到0之间的无理数有 个.?
5.把下列各数分别填入相应的集合里.
-5,-2.626
626
662…,0,π,-74,0.12,|-6|.
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
2 平方根
第1课时 算术平方根
1.下列各式中无意义的是( )
A.
B.
C.
D.
2.的值等于( )
A.
B.-
C.±
D.
3.(2020泰安泰山期末)的算术平方根的倒数是( )
A.4
B.
C.2
D.
4.有一个数值转换器,原理如图所示,当输入的数为16时,输出的数为 .?
5.(2020临淄期末)已知a,b满足(a-1)2+=0,则ab= .?
6.计算:
(1) (2) (3)
(4)
(5)
第2课时 平方根
1.(2020垦利期末)16的平方根是( )
A.±4
B.±2
C.4
D.-4
2.(2021泰安东平实验中学月考)下列语句正确的是( )
A.27的平方根是3
B.-9是-81的平方根
C.15是225的平方根
D.(-8)2的算术平方根是64
3.(2020莱州期末)的平方根是( )
A.±
B.
C.±
D.
4.(2020泰安泰山期末)若4x2-25=0,则x= .?
5.(2020东营胜利一中期末)的平方根是 .?
6.若2m-4与3m-1是同一个数两个不同的平方根,求m的值.
3 立方根
1.-27的立方根是( )
A.-3
B.3
C.-9
D.9
2.(2020胜利一中期末)下列说法正确的是( )
A.9的算术平方根是3
B.(-3)2的平方根是-3
C.1的立方根是±1
D.-4的平方根是±2
3.(2020威海乳山期末)的平方根为( )
A.2
B.±2
C.
D.±
4.(2021泰安东平实验中学月考)的立方根是 .?
5.(2021泰安东平实验中学月考)-8的立方根与的平方根之和是 . ?
6.(2020高青期末)已知4a+1的平方根是±3,b-1的算术平方根为2.
(1)求a与b的值;
(2)求2a+b-1的立方根.
4 估算
1.若k<
B.9
C.10
D.11
2.比较三个数-3,-π,-的大小,下列结论正确的是( )
A.-π>-3>-
B.->-3>-π
C.->-π>-3
D.-3>-π>-
3.(2020莱州期末)写出-和之间的所有整数 .?
4.若a是的整数部分,则a(a+6)= .?
5.(2020河口期末)已知m是的整数部分,n是的小数部分,则m+n= .?
6.已知a为的整数部分,b-1是400的算术平方根,求a+b的平
方根.
5 用计算器开方
1.(2020临淄期末)在计算器上依次按键,得到的结果是( )
A.8
B.-8
C.4
D.-4
2.(2020莱州期末)在计算器上依次按键,显示的结果为( )
A.-5
B.5
C.-25
D.25
3.用计算器计算:≈ .(精确到0.01)?
4.用计算器计算:+-≈ .(精确到0.01)?
5.用计算器比较:5,4,3的大小(用“<”连接)
.?
6.在,,,…,中无理数的个数是 .?
6 实数
第1课时 实数及其性质
1.下列各数中,是无理数的是( )
A.3.141
5
B.
C.
D.
2.在实数:,π,,,2π,,0.36,0.373
773
777
3…(相邻两个3之间7的个数逐次加1),-,中,无理数的个数为( )
A.4
B.5
C.6
D.7
3.-3的相反数是 ,绝对值是 .?
4.已知与互为相反数,则x的值为 .?
5.(2020胜利一中期末)如图所示,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以点O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为 .?
第2课时 实数的运算与大小比较
1.(2019泰安)在实数|-3.14|,-3,-,π中,最小的数是( )
A.-
B.-3
C.|-3.14|
D.π
2.文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A.5
B.6
C.7
D.8
3.比较大小: 0.5.?
4.|-2|--= .?
5.(1)计算:-;
(2)计算:|-5|-(-1)0++;
(3)求x的值:(x-2)2=9.
第五章 位置与坐标
1 确定位置
1.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排
B.第3组第1排
C.第2组第3排
D.第2组第2排
2.(2021泰安东平实验中学月考)下列数据不能确定物体位置的是( )
A.电影票5排8号
B.北偏东30°
C.希望路25号
D.东经118°,北纬40°
3.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为( )
A.同一排
B.前后在同一条直线上
C.中间隔六个人
D.前后隔六排
4.如图所示是某地区简图的一部分,图中“故宫”所在的区域表示为E7,那么“鼓楼”所在的区域可以表示为 .?
第4题图
5.如图所示,O对应的有序数对为(1,3),有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来为 .?
第5题图
2 平面直角坐标系
第1课时 平面直角坐标系
1.(2020泰安泰山期末)点P(m+3,m+1)在直角坐标系的y轴上,则点P的坐标为( )
A.(-2,0)
B.(3,0)
C.(0,3)
D.(0,-2)
2.(2020高青期末)在平面直角坐标系内,点P(x,x+5)的位置一定不在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如图所示,在平面直角坐标系中,点A的坐标是 .?
4.点P(3,-2)到y轴的距离为 个单位.?
5.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2)四个点.
(1)线段AB,CD有什么关系?
(2)顺次连接A,B,C,D四点组成的图形,你认为它像什么?
第2课时 建立恰当的平面直角坐标系
1.如图所示,若点E的坐标为(-2,2),点F的坐标为(-1,0),则点G的坐标为( )
第1题图
A.(2,1)
B.(-2,1)
C.(2,-1)
D.(2,3)
2.(2020胜利一中期末)甲和乙下棋,甲执白子,乙执黑子.如图所示,一共下了7枚棋子,棋盘中心黑子的位置用(-1,0)表示,其右下角黑子的位置用(0,-1)表示.甲将第4枚白子放入棋盘后,所有棋子构成一个轴对称图形.他放的位置是( )
第2题图
A.(-1,1)
B.(-2,1)
C.(1,-2)
D.(-1,-2)
3.如图所示,在△OAB中,OA=AB=5,点B(6,0),则点A的坐标是
. ?
第3题图
4.如图所示,已知点A的坐标为(-2,2),点B的坐标为(-1,-2),则点C的坐标是 .?
第4题图
5.(2021泰安东平实验中学月考)如图所示,△ABC在正方形网格中,每个小正方形的边长为1个单位长度.若A(0,3),按要求回答下列
问题.
(1)在图中建立恰当的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.
3 轴对称与坐标变化
1.在平面直角坐标系中,点A的坐标为(-2,3),点B的坐标为(-2,-3),那么点A和点B的位置关系是( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.关于坐标轴和原点都不对称
2.(2020高青期末)已知点A(a-2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1
B.3
C.-1
D.5
3.已知点P1,P2关于x轴对称,点P2,P3关于y轴对称,点P3的坐标为(-3,4),则点P1的坐标为 .?
4.(2020胜利一中期末)已知点A(a-1,5)与点B(2,b-1)关于x轴对称,则(a+b)2
020= .?
5.已知等腰直角△ABC的斜边AB在x轴上,点C在y轴上,若点A的坐标是(-3,0),则点B的坐标为 .?
6.(2020垦利期末)如图所示,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点坐标分别为A(-4,1),B(-3,3),C(-1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1,B1,C1,写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,并求出△CC1C2的面积.
第六章 一次函数
1 函数
1.下列两个变量之间,不存在函数关系的是( )
A.一天的气温与时间之间的关系
B.一个正数的平方根与这个正数之间的关系
C.圆的面积与圆的周长之间的关系
D.速度一定,汽车行驶的路程与行驶时间之间的关系
2.(2020河口期末)如图所示,在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGD,动点P从点A出发,沿A→E→F→G→C→B的路线,绕多边形的边匀速运动到点B时停止,则△ABP的面积S随着时间t变化的函数图象大致是( )
3.某市的夏天经常刮台风,给人们的出行带来很多不便,小欣了解到该市去年8月16日连续12个小时的风力变化情况,并画出了风力随时间变化的图象(如图所示),则下列说法正确的是( )
A.8时风力最小
B.在8时至12时,风力最大为5级
C.在12时至14时,风力最大为7级
D.8时至14时,风力不断增大
4.公式L=L0+KP表示当重力为P的物体作用在弹簧上时弹簧的长度,L0代表弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
A.L=10+0.5P
B.L=10+5P
C.L=80+0.5P
D.L=80+5P
5.(2020垦利期末)小明从家沿笔直的公路骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,如图所示是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 m;?
(2)小明在书店停留了 min;?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
2 一次函数
1.下列函数中,是一次函数的有( )
①y=;②y=4x;③y=x;④y=+1;⑤y=2x2-1.
A.1个
B.2个
C.3个
D.4个
2.下列y关于x的函数中,是正比例函数的为( )
A.y=x2
B.y=
C.y=x
D.y=x+1
3.已知A,B两地相距30
km,小明以6
km/h的速度从A地步行到B地,记小明步行的距离为y
km,步行的时间为x
h.则y与x之间的函数表达式是
,y是x的
函数,自变量的取值范围是 .?
4.某水库的水位在5小时内持续上涨,初始的水位高度为6
m,水位以0.3
m/h
的速度匀速上升,则水库的水位高度y
m与时间x
h(0≤x≤5)的函数关系为 .?
5.当m,n为何值时,y=(m-1)+n.(注:指数为m2)
(1)是一次函数;
(2)是正比例函数.
3 一次函数的图象
第1课时 正比例函数的图象与性质
1.正比例函数y=kx的图象如图所示,则k的取值范围是( )
第1题图
A.k>0
B.k<0
C.k>1
D.k<1
2.关于正比例函数y=-3x,下列结论正确的是( )
A.图象不经过原点
B.y随x的增大而增大
C.图象经过第二、四象限
D.当x=时,y=1
3.经过以下一组点坐标可以画出函数y=2x图象的是( )
A.(0,0)和(2,1)
B.(1,2)和(-1,-2)
C.(1,2)和(2,1)
D.(-1,2)和(1,2)
4.已知正比例函数y=(k-2)x,若y随x的增大而增大,则k的取值范围是 .?
5.如图所示,三个正比例函数的图象对应的表达式分别为①y=ax,②y=bx,③y=cx,则a,b,c的大小关系是 .?
第5题图
6.已知正比例函数y=kx.
(1)若函数图象经过第二、四象限,则k的范围是什么?
(2)若点(1,-2)在它的图象上,求它的表达式.
第2课时 一次函数的图象与性质
1.(2020莱州期末)如图所示,表示一次函数的是( )
2.(2020河口期末)关于函数y=-2x+1,下列结论正确的是( )
A.图象经过点(-2,1)
B.y随x的增大而增大
C.图象不经过第三象限
D.图象不经过第二象限
3.(2020高青期末)已知点(k,b)为第二象限内的点,则一次函数y=-kx+b的图象大致是( )
4.(2020莱州期末)在平面直角坐标系中,已知一次函数y=kx-b(k<0)的图象经过P1(-1,y1),P2(2,y2)两点,则y1 y2(填“>”“=”或“<”).?
5.一次函数y=-3x-9的图象与x轴的交点坐标是 ,与y轴的交点坐标是 .?
6.已知,一次函数y=2x-4.
(1)在给定的直角坐标系中画出这个函数的图象;
(2)根据图象,说出函数的三条性质(或图象特征).
4 确定一次函数的表达式
1.已知一次函数y=kx-2,当x=2时,y=1,则k的值为( )
A.-
B.
C.
D.
2.如图所示,某正比例函数的图象过点M(-2,1),则此正比例函数的表达式为( )
第2题图
A.y=-x
B.y=x
C.y=-2x
D.y=2x
3.(2020胜利一中期末)如图所示,直线l是一次函数y=kx+b(k≠0)的图象,则b= .?
第3题图
4.(2020垦利期末)将一次函数y=2x-3的图象沿y轴向上平移5个单位后,得到的图象对应的函数表达式为 .?
5.在平面直角坐标系中,如果点(x,4),(0,8),(-4,0)在同一条直线上,则x= .?
6.一次函数的图象经过点A(3,7)和B(0,-2)两点.
(1)求出该一次函数的表达式;
(2)判断是否在这个函数的图象上.
5 一次函数的应用
1.一根蜡烛长30
cm,点燃后每小时燃烧5
cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(h)之间的函数关系用图象可以表示为( )
2.若一次函数y=kx+3(k为常数且k≠0)的图象经过点(-2,0),则关于x的方程k(x-5)+3=0的解为( )
A.x=-5
B.x=-3
C.x=3
D.x=5
3.如图所示是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象,下列说法:①买2件时甲、乙两家售价一样;②买1件时选乙家的产品合算;③买3件时选甲家的产品合算;④买1件时,售价约为3元.其中正确的说法是 (填写序号).?
4.(2020泰安泰山期末)某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费
200元.若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为
x
km,通过铁路运输和公路运输需交总运费y1元和y2元.
(1)求y1和y2关于x的表达式;
(2)若A地到B地的路程为120
km,哪种运输可以节省总运费?
参考答案
第一章 三角形
1 认识三角形
第1课时 三角形及其内角和
1.C 2.B 3.C 4.75° 5.14°
6.解:由三角形内角和定理,得∠A+∠B+∠C=180°,
则
解得∠A=15°,∠B=65°,∠C=100°.
第2课时 三角形的分类及直角
三角形的性质
1.A 2.A 3.D 4.55°
5.解:因为ED⊥AB,所以∠ADE=90°.因为∠C=90°,∠B=55°,所以
∠A=35°.所以∠AED=55°.
第3课时 三角形的三边关系
1.B 2.C 3.A 4.7 5.3
6.解:(1)设底边长为x
cm,则腰长为2x
cm.由题意,得2x+2x+x=20,解得x=4.
所以2x=8.
所以三角形三边的长分别为8
cm,8
cm,4
cm.
(2)若腰长为5
cm,则底边长为20-5-5=10
cm.
而5+5=10,所以不能围成腰长为5
cm的等腰三角形.
若底边长为5
cm,则腰长为×(20-5)=cm.此时能围成等腰三角形,三边长分别为5
cm,cm,cm.
第4课时 三角形中的
三条重要线段
1.D 2.B 3.140° 4.2
5.解:因为∠B=42°,∠C=70°,
所以∠BAC=180°-∠B-∠C=68°.
因为AE平分∠BAC,
所以∠CAE=∠BAC=34°.
因为AD是BC边上的高,
所以∠ADC=90°.
因为∠C=70°,
所以∠CAD=180°-∠ADC-∠C=20°.
所以∠DAE=∠CAE-∠CAD=34°-20°=14°.
2 图形的全等
1.B 2.B 3.30 4.70°
5.解:(1)因为△ABC≌△DEF,
所以∠D=∠A=68°,∠DFE=∠ACB=90°-68°=22°.
(2)因为△ABC≌△DEF,
所以DE=AB=5,
EF=BC=9.
所以CE=EF-CF=9-6=3.
3 探索三角形全等的条件
第1课时 边边边
1.D 2.C
3.AB=DF(或AD=BF答案不唯一)
4.解:全等;平行.理由如下:
因为BE=FC,
所以BE+CE=CE+CF.
所以BC=EF.
在△ABC和△DFE中,
所以△ABC≌△DFE(SSS).
所以∠B=∠F.
所以AB∥DF.
第2课时 角边角或角角边
1.C 2.D
3.∠B=∠C(答案不唯一)
4.解:因为四边形ABCD为正方形,
所以AB=BC,∠ABC=90°.
因为AE⊥BE,CF⊥BF,
所以∠AEB=∠BFC=90°.
所以∠EAB+∠ABE=90°,
∠ABE+∠FBC=90°.
所以∠EAB=∠FBC.
在△ABE和△BCF中,
所以△ABE≌△BCF.
所以BE=CF=2,
AE=BF=1.
所以EF=BE+BF=3.
第3课时 边角边
1.B 2.C 3.①③④
4.证明:因为∠BAE=∠DAC,
所以∠BAE-∠CAE
=∠DAC-∠CAE,
即∠BAC=∠DAE.
在△ABC和△ADE中,
因为AB=AD,
∠BAC=∠DAE,AC=AE,
所以△ABC≌△ADE(SAS).
所以∠C=∠E.
4 三角形的尺规作图
1.C 2.③①②
3.解:如图所示,△ABC为所作.
5 利用三角形全等测距离
1.B 2.C 3.15
4.解:(1)测量图案,如图所示.
(2)在湖岸上选一点O,连接BO并延长到C使OC=BO,连接AO并延长到点D使OD=AO,连接CD,则CD=AB.测量DC的长度即为AB的长度.
(3)设DC=m,因为BO=CO,∠AOB=∠DOC,AO=DO,根据SAS,
所以△AOB≌△DOC.
所以AB=CD=m.
第二章 轴对称
1 轴对称现象
1.D 2.C 3.3 4.书
5.解:如图所示,答案不唯一.
2 探索轴对称的性质
1.B 2.7.5 3.90° CF=CD
4.解:(1)由折叠的性质可知,DE垂直平分线段AB,
且DA=DB,
所以△ACD的周长为DA+DC+AC=DB+DC+AC=BC+AC=14
cm.
(2)设∠CAD=x,则∠BAD=2x,
因为DA=DB,
所以∠B=∠BAD=2x.
在Rt△ABC中,∠B+∠BAC=90°,
即2x+2x+x=90°,x=18°.
所以∠B=2x=36°.
3 简单的轴对称图形
第1课时 线段垂直平分线的性质
1.A 2.D 3.15
4.
解:如图所示,作AC,BC的
垂直平分线,分别交AB于点D,E,则点D,E即为所求.
5.解:如图所示,点P即为所求.
第2课时 角平分线的性质
1.A 2.C 3.D 4.4
第3课时 等腰三角形的
性质与判定
1.A 2.4
cm 3.108°
4.解:△APQ是等腰三角形.
证明:因为∠QDB=∠DQC+∠C,∠PDC=∠B+∠P,
又因为AB=AC,
所以∠B=∠C.
所以∠P=∠DQC=∠AQP.
所以AP=AQ.
所以△APQ是等腰三角形.
4 利用轴对称进行设计
1.B 2.4
3.解:如图所示:
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
1.A 2.B 3.25 4.14
5.解:在Rt△ABE中,
由勾股定理,得AE2=AB2+BE2=402+92=1
681.所以AE=41.而AB+BE=40+9=49,因为49-41=8,
所以标牌上填的数是8.
第2课时 勾股定理的验证与应用
1.D 2.12 3.4
2 一定是直角三角形吗
1.C 2.C 3.②④ 4.直角
5.16,63,65
6.解:如图所示,连接AC,
因为∠ADC=90°,在Rt△ACD中,由勾股定理,得AC2=AD2+CD2=82+62=100,所以AC=10
m.在△ABC中,AC2+BC2=102+242=100+576=676,AB2=262=676,所以AC2+BC2=AB2.所以△ABC是直角三角形,其中∠ACB=90°.所以四边形ABCD的面积为S=S△ABC-S△ACD=AC·BC-AD·CD=×10×24-×8×6=120-24=96(m2).96×200=19
200(元),所以学校需要投入资金19
200元购买草皮.
3 勾股定理的应用举例
1. 2.125
cm
3.解:设BC为h
m,
在Rt△BCD中,BC=h,BD=AB=h+1,DC=3,
由勾股定理,得BD2=DC2+BC2,即(h+1)2=h2+32,解得h=4.因此湖深BC为4
m.
第四章 实数
1 无理数
1.D 2.B 3.D 4.无数
5.解:(1)正数集合:{π,0.12,|-6|,…};
(2)负数集合:{-5,
-2.626
626
662…,-74,…};
(3)有理数集合:{-5,0,-74,0.12,|-6|,…};
(4)无理数集合:
{-2.626
626
662…,π,…}.
2 平方根
第1课时 算术平方根
1.B 2.A 3.D 4. 5.1
6.解:(1)=8.
(2)==2.
(3)=0.9.
(4)=.
(5)=10-2.
第2课时 平方根
1.A 2.C 3.C 4.± 5.±2
6.解:根据题意,得
(2m-4)+(3m-1)=0,
解得m=1.所以m的值为1.
3 立方根
1.A 2.A 3.D 4.2
5.1或-5
6.解:(1)因为4a+1的平方根是±3,所以4a+1=9,解得a=2.
因为b-1的算术平方根为2,
所以b-1=4,解得b=5.
(2)因为a=2,b=5,所以2a+b-1=2×2+5-1=8.因为=2,所以2a+b-1的立方根是2.
4 估算
1.B 2.B 3.-1,0,1 4.27 5.
6.解:因为的整数部分是4,即a=4,因为b-1==20,所以b=21.所以a+b=25.因为25的平方根是±5.即a+b的平方根是±5.
5 用计算器开方
1.C 2.A 3.16.15 4.0.91
5.3<4<5
6.1
966
6 实数
第1课时 实数及其性质
1.D 2.A 3.3- 3-
4.3 5.
第2课时 实数的运算与大小比较
1.B 2.B 3.> 4.3
5.解:(1)-=2-(-2)=4.
(2)原式=5-1+9-3=10.
(3)开方,得x-2=3,或x-2=-3,
解得x=5或x=-1.
第五章 位置与坐标
1 确定位置
1.C 2.B 3.A
4.D6 5.HELLO
2 平面直角坐标系
第1课时 平面直角坐标系
1.D 2.D 3.(-2,3)
4.3
5.解:描出A,B,C,D四个点,如图所示.
(1)由图,知AB∥CD,AB=CD.
(2)由A,B,C,D构成的图形像“Z”字.
第2课时 建立恰当的平面直
角坐标系
1.A 2.A 3.(3,4) 4.(2,1)
5.解:(1)建立平面直角坐标系如图所示.
(2)根据坐标系可得出B(-3,-1),C(1,1).
(3)S△ABC=4×4-×4×2-×3×4-×1×2=5.
3 轴对称与坐标变化
1.A 2.B 3.(3,-4) 4.1
5.(3,0)
6.解:(1)如图所示,△A1B1C1即为所求.
点A1,B1,C1的坐标分别为A1(-4,-1),B1(-3,-3),C1(-1,-2),
(2)如图所示,△CC1C2的面积是×2×4=4.
第六章 一次函数
1 函数
1.B 2.B 3.C 4.A
5.解:(1)根据图象,学校的纵坐标为1
500,小明家的纵坐标为0,
故小明家到学校的路程是1
500
m.
(2)根据题意,小明在书店停留的时间为从8
min到12
min,
故小明在书店停留了12-8=4(min).
(3)因为1
200+(1
200-600)+(1
500-600)=1
200+600+900=2
700(m),
所以小明一共行驶的总路程为2
700
m,共用了14
min.
2 一次函数
1.C 2.C
3.y=6x 正比例 0≤x≤5
4.y=6+0.3x
5.解:(1)当m2=1且m-1≠0时,y=(m-1)+n是一次函数,即m=-1.所以当m=-1,n为任意实数时,y=(m-1)+n是一次函数.
(2)当m2=1且m-1≠0,且n=0时,y=(m-1)+n是正比例函数,即m=-1且n=0,所以当m=-1且n=0时,y=(m-1)+n是正比例函数.
3 一次函数的图象
第1课时 正比例函数的
图象与性质
1.A 2.C 3.B 4.k>2
5.c>b>a
6.解:(1)因为函数图象经过第二、四象限,所以k<0.
(2)当x=1时,y=-2,
则k=-2,
即y=-2x.
第2课时 一次函数的图象与性质
1.B 2.C 3.C 4.>
5.(-3,0) (0,-9)
6.解:(1)令y=2x-4=0,解得x=2,
令x=0,解得y=-4,
所以一次函数与两坐标轴的交点坐标为(2,0)和(0,-4),所以图象如图所示.
(2)性质:y随x的增大而增大;
与两坐标轴围成的面积为4;
函数图象不经过第二象限.
4 确定一次函数的表达式
1.D 2.A 3.1
4.y=2x+2 5.-2
6.解:(1)设一次函数的表达式为
y=kx+b(k≠0),
根据题意,将A,B两点的坐标分别代入,得
解得
所以一次函数的表达式为y=3x-2.
(2)对于y=3x-2,
当x=时,
y=3×-2=-1,
所以点在一次函数y=3x-2的图象上.
5 一次函数的应用
1.B 2.C 3.①②③
4.解:(1)根据题意,得y1=
15x+400+200=15x+600;
y2=25x+100(x>0).
(2)当x=120时,
y1=15×120+600=2
400,
y2=25×120+100=3
100,
因为y1
