广东省广州市西关重点外国语高中2022届高三上学期8月月考数学试题(Word版含答案)
文档属性
| 名称 | 广东省广州市西关重点外国语高中2022届高三上学期8月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 886.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 12:23:16 | ||
图片预览




文档简介
2022届西关外国语高中8月月考
数学试卷(问卷)
一?单项选择题:本题包括8小题,每小题5分,共40分,每小题只有一个选项符合题意.
1.
已知集合,集合,则(
)
A.
B.
C.
D.
2.
已知复数,其中是虚数单位,则的共轭复数虚部为(
)
A.
B.
3
C.
D.
3.
展开式中的常数项为-160,则a=(
)
A.
-1
B.
1
C.
±1
D.
2
4.
17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得(
)
A.
B.
C.
D.
5.
已知正项等比数列满足:,若数列中存在两项使得,
则的最小值为
A.
9
B.
C.
D.
6.
在中,角A,B,C的对边分别为a,b,c,的面积为S,且,则tanC=(
)
A.
B.
C.
D.
7.
已知定义在上的函数,,,,则,,的大小关系为(
)
A.
B.
C.
D.
8.
已知是可导的函数,且,对于恒成立,则下列不等关系正确的是(
)
A.
,
B.
,
C.
,
D.
,
二?多项选择题:本题包括4小题,每小题5分,共20分,每小题至少有两个选项符合题意,全对得5分,选得2分,选错不得分.
9.
下列说法正确的是(
)
A.
集合的真子集个数为
B.
“函数恒成立”是“”的必要条件
C.
已知,则函数在定义域上为单调增函数
D.
命题“,”的否定是“,”
10.
在无穷数列中,若,总有,此时定义为“阶梯数列”.设为“阶梯数列”,且,,,则(
)
A.
B.
C.
D.
11.
已知椭圆C:内一点M(1,2),直线与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是(
)
A.
椭圆焦点坐标为(2,0)?(-2,0)
B.
椭圆C的长轴长为
C.
直线的方程为
D.
12.
如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.
直线BD1⊥平面A1C1D
B.
三棱锥P﹣A1C1D的体积为定值
C.
异面直线AP与A1D所成角的取值范用是[45°,90°]
D.
直线C1P与平面A1C1D所成角的正弦值的最大值为
三?填空题(本题包括4小题,每小题5分,共20分)
13.
设为单位向量,且,则________.
14.
已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种.
15.
在三棱锥中,,,,.平面平面,若球是三棱锥的外接球,则球的半径为_________.
16.
关于的方程在上有两个不相等的实根,则实数的取值范围______.
四?解答题(本题包括6小题.共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知数列的前n项和为,,设
(1)判断数列否为等差数列,并说明理由.
(2)求数列前n项和.
18.
已知的三个内角所对的边分别为,,,且满足.
(1)求角;
(2)若,且边上的中线的长为,求此时的面积.
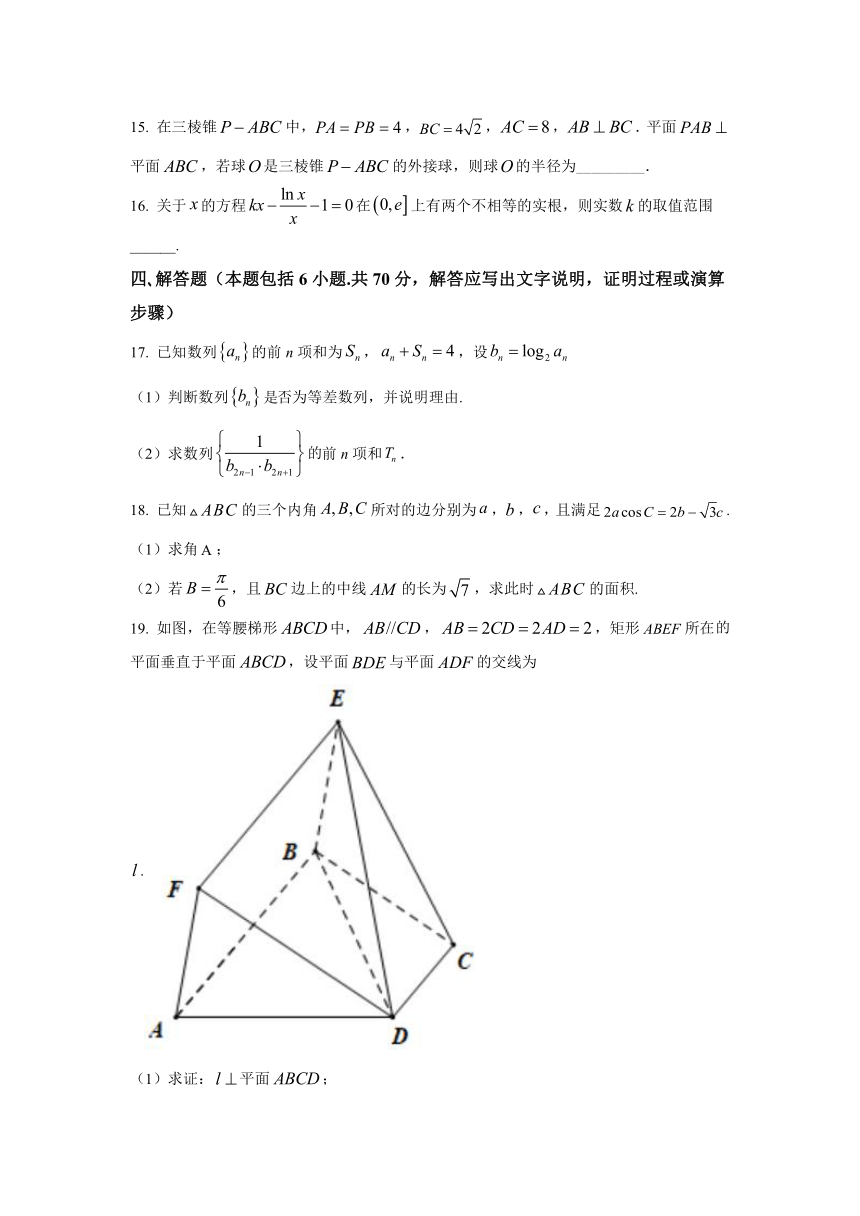
19.
如图,在等腰梯形中,,,矩形所在平面垂直于平面,设平面与平面的交线为.
(1)求证:平面;
(2)若的长度为,求二面角的大小.
20.
2020新年伊始爆发的新冠疫情让广大民众意识到健康的重要性,云南省全面开展爱国卫生7个专项行动及健康文明生活的6条新风尚行动,其中“科学健身”鼓励公众每天进行60分钟的体育锻炼.某社区从居民中随机抽取了若干名,统计他们的平均每天锻炼时间(单位:分钟/天),得到的数据如下表:(所有数据均在0~120分钟/天之间)
平均锻炼时间
人数
27
39
a
b
45
15
频率
009
0.13
0.38
c
0.15
0.05
(1)求,,的值;
(2)为了鼓励居民进行体育锻炼,该社区决定对运动时间不低于分钟的居民进行奖励,为使30%的人得到奖励,试估计的取值?
(3)在第(2)问的条件下,以频率作为概率,在该社区得到奖励的人中随机抽取4人,设这4人中日均锻炼时间不低于80分钟的人数为,求的分布列和数学期望.
21.
已知椭圆:,是坐标原点,,分别为椭圆的左、右焦点,点在椭圆上,过作的外角的平分线的垂线,垂足为,且.
(1)求椭圆的方程:
(2)设直线:与椭圆交于,两点,且直线,,的斜率之和为0(其中为坐标原点).
①求证:直线经过定点,并求出定点坐标:
②求面积的最大值.
22.
已知函数.
(1)讨论函数f(x)的单调性;
(2)当x>0时,恒成立,求实数a的取值范围.
2022届西关外国语高中8月月考
数学试卷(问卷)
答案版
一?单项选择题:本题包括8小题,每小题5分,共40分,每小题只有一个选项符合题意.
1.
已知集合,集合,则(
)
A.
B.
C.
D.
答案:D
2.
已知复数,其中是虚数单位,则的共轭复数虚部为(
)
A.
B.
3
C.
D.
答案:B
3.
展开式中的常数项为-160,则a=(
)
A.
-1
B.
1
C.
±1
D.
2
答案:B
4.
17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得(
)
A.
B.
C.
D.
答案:C
5.
已知正项等比数列满足:,若数列中存在两项使得,
则的最小值为
A.
9
B.
C.
D.
答案:D
6.
在中,角A,B,C的对边分别为a,b,c,的面积为S,且,则tanC=(
)
A.
B.
C.
D.
答案:C
7.
已知定义在上的函数,,,,则,,的大小关系为(
)
A.
B.
C.
D.
答案:D
8.
已知是可导的函数,且,对于恒成立,则下列不等关系正确的是(
)
A.
,
B.
,
C.
,
D.
,
答案:C
二?多项选择题:本题包括4小题,每小题5分,共20分,每小题至少有两个选项符合题意,全对得5分,选得2分,选错不得分.
9.
下列说法正确的是(
)
A.
集合的真子集个数为
B.
“函数恒成立”是“”的必要条件
C.
已知,则函数在定义域上为单调增函数
D.
命题“,”的否定是“,”
答案:BD
10.
在无穷数列中,若,总有,此时定义为“阶梯数列”.设为“阶梯数列”,且,,,则(
)
A.
B.
C.
D.
答案:ACD
11.
已知椭圆C:内一点M(1,2),直线与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是(
)
A.
椭圆焦点坐标为(2,0)?(-2,0)
B.
椭圆C的长轴长为
C.
直线的方程为
D.
答案:BCD
12.
如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.
直线BD1⊥平面A1C1D
B.
三棱锥P﹣A1C1D的体积为定值
C.
异面直线AP与A1D所成角的取值范用是[45°,90°]
D.
直线C1P与平面A1C1D所成角的正弦值的最大值为
答案:ABD
三?填空题(本题包括4小题,每小题5分,共20分)
13.
设为单位向量,且,则________.
答案:
14.
已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种.
答案:20
15.
在三棱锥中,,,,.平面平面,若球是三棱锥的外接球,则球的半径为_________.
答案:4
16.
关于的方程在上有两个不相等的实根,则实数的取值范围______.
答案:
四?解答题(本题包括6小题.共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知数列的前n项和为,,设
(1)判断数列否为等差数列,并说明理由.
(2)求数列前n项和.
答案:(1)是,理由见解析;(2).
18.
已知的三个内角所对的边分别为,,,且满足.
(1)求角;
(2)若,且边上的中线的长为,求此时的面积.
答案:(1);(2)
19.
如图,在等腰梯形中,,,矩形所在平面垂直于平面,设平面与平面的交线为.
(1)求证:平面;
(2)若的长度为,求二面角的大小.
答案:(1)详见解析;(2).
20.
2020新年伊始爆发的新冠疫情让广大民众意识到健康的重要性,云南省全面开展爱国卫生7个专项行动及健康文明生活的6条新风尚行动,其中“科学健身”鼓励公众每天进行60分钟的体育锻炼.某社区从居民中随机抽取了若干名,统计他们的平均每天锻炼时间(单位:分钟/天),得到的数据如下表:(所有数据均在0~120分钟/天之间)
平均锻炼时间
人数
27
39
a
b
45
15
频率
009
0.13
0.38
c
0.15
0.05
(1)求,,的值;
(2)为了鼓励居民进行体育锻炼,该社区决定对运动时间不低于分钟的居民进行奖励,为使30%的人得到奖励,试估计的取值?
(3)在第(2)问的条件下,以频率作为概率,在该社区得到奖励的人中随机抽取4人,设这4人中日均锻炼时间不低于80分钟的人数为,求的分布列和数学期望.
答案:(1),;;(2);(3)分布列见解析;期望为.
21.
已知椭圆:,是坐标原点,,分别为椭圆的左、右焦点,点在椭圆上,过作的外角的平分线的垂线,垂足为,且.
(1)求椭圆的方程:
(2)设直线:与椭圆交于,两点,且直线,,的斜率之和为0(其中为坐标原点).
①求证:直线经过定点,并求出定点坐标:
②求面积的最大值.
答案:(1);(2)①证明见解析,;②.
22.
已知函数.
(1)讨论函数f(x)的单调性;
(2)当x>0时,恒成立,求实数a的取值范围.
答案:(1)见解析;(2)(﹣∞,e﹣1].
数学试卷(问卷)
一?单项选择题:本题包括8小题,每小题5分,共40分,每小题只有一个选项符合题意.
1.
已知集合,集合,则(
)
A.
B.
C.
D.
2.
已知复数,其中是虚数单位,则的共轭复数虚部为(
)
A.
B.
3
C.
D.
3.
展开式中的常数项为-160,则a=(
)
A.
-1
B.
1
C.
±1
D.
2
4.
17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得(
)
A.
B.
C.
D.
5.
已知正项等比数列满足:,若数列中存在两项使得,
则的最小值为
A.
9
B.
C.
D.
6.
在中,角A,B,C的对边分别为a,b,c,的面积为S,且,则tanC=(
)
A.
B.
C.
D.
7.
已知定义在上的函数,,,,则,,的大小关系为(
)
A.
B.
C.
D.
8.
已知是可导的函数,且,对于恒成立,则下列不等关系正确的是(
)
A.
,
B.
,
C.
,
D.
,
二?多项选择题:本题包括4小题,每小题5分,共20分,每小题至少有两个选项符合题意,全对得5分,选得2分,选错不得分.
9.
下列说法正确的是(
)
A.
集合的真子集个数为
B.
“函数恒成立”是“”的必要条件
C.
已知,则函数在定义域上为单调增函数
D.
命题“,”的否定是“,”
10.
在无穷数列中,若,总有,此时定义为“阶梯数列”.设为“阶梯数列”,且,,,则(
)
A.
B.
C.
D.
11.
已知椭圆C:内一点M(1,2),直线与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是(
)
A.
椭圆焦点坐标为(2,0)?(-2,0)
B.
椭圆C的长轴长为
C.
直线的方程为
D.
12.
如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.
直线BD1⊥平面A1C1D
B.
三棱锥P﹣A1C1D的体积为定值
C.
异面直线AP与A1D所成角的取值范用是[45°,90°]
D.
直线C1P与平面A1C1D所成角的正弦值的最大值为
三?填空题(本题包括4小题,每小题5分,共20分)
13.
设为单位向量,且,则________.
14.
已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种.
15.
在三棱锥中,,,,.平面平面,若球是三棱锥的外接球,则球的半径为_________.
16.
关于的方程在上有两个不相等的实根,则实数的取值范围______.
四?解答题(本题包括6小题.共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知数列的前n项和为,,设
(1)判断数列否为等差数列,并说明理由.
(2)求数列前n项和.
18.
已知的三个内角所对的边分别为,,,且满足.
(1)求角;
(2)若,且边上的中线的长为,求此时的面积.
19.
如图,在等腰梯形中,,,矩形所在平面垂直于平面,设平面与平面的交线为.
(1)求证:平面;
(2)若的长度为,求二面角的大小.
20.
2020新年伊始爆发的新冠疫情让广大民众意识到健康的重要性,云南省全面开展爱国卫生7个专项行动及健康文明生活的6条新风尚行动,其中“科学健身”鼓励公众每天进行60分钟的体育锻炼.某社区从居民中随机抽取了若干名,统计他们的平均每天锻炼时间(单位:分钟/天),得到的数据如下表:(所有数据均在0~120分钟/天之间)
平均锻炼时间
人数
27
39
a
b
45
15
频率
009
0.13
0.38
c
0.15
0.05
(1)求,,的值;
(2)为了鼓励居民进行体育锻炼,该社区决定对运动时间不低于分钟的居民进行奖励,为使30%的人得到奖励,试估计的取值?
(3)在第(2)问的条件下,以频率作为概率,在该社区得到奖励的人中随机抽取4人,设这4人中日均锻炼时间不低于80分钟的人数为,求的分布列和数学期望.
21.
已知椭圆:,是坐标原点,,分别为椭圆的左、右焦点,点在椭圆上,过作的外角的平分线的垂线,垂足为,且.
(1)求椭圆的方程:
(2)设直线:与椭圆交于,两点,且直线,,的斜率之和为0(其中为坐标原点).
①求证:直线经过定点,并求出定点坐标:
②求面积的最大值.
22.
已知函数.
(1)讨论函数f(x)的单调性;
(2)当x>0时,恒成立,求实数a的取值范围.
2022届西关外国语高中8月月考
数学试卷(问卷)
答案版
一?单项选择题:本题包括8小题,每小题5分,共40分,每小题只有一个选项符合题意.
1.
已知集合,集合,则(
)
A.
B.
C.
D.
答案:D
2.
已知复数,其中是虚数单位,则的共轭复数虚部为(
)
A.
B.
3
C.
D.
答案:B
3.
展开式中的常数项为-160,则a=(
)
A.
-1
B.
1
C.
±1
D.
2
答案:B
4.
17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得(
)
A.
B.
C.
D.
答案:C
5.
已知正项等比数列满足:,若数列中存在两项使得,
则的最小值为
A.
9
B.
C.
D.
答案:D
6.
在中,角A,B,C的对边分别为a,b,c,的面积为S,且,则tanC=(
)
A.
B.
C.
D.
答案:C
7.
已知定义在上的函数,,,,则,,的大小关系为(
)
A.
B.
C.
D.
答案:D
8.
已知是可导的函数,且,对于恒成立,则下列不等关系正确的是(
)
A.
,
B.
,
C.
,
D.
,
答案:C
二?多项选择题:本题包括4小题,每小题5分,共20分,每小题至少有两个选项符合题意,全对得5分,选得2分,选错不得分.
9.
下列说法正确的是(
)
A.
集合的真子集个数为
B.
“函数恒成立”是“”的必要条件
C.
已知,则函数在定义域上为单调增函数
D.
命题“,”的否定是“,”
答案:BD
10.
在无穷数列中,若,总有,此时定义为“阶梯数列”.设为“阶梯数列”,且,,,则(
)
A.
B.
C.
D.
答案:ACD
11.
已知椭圆C:内一点M(1,2),直线与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是(
)
A.
椭圆焦点坐标为(2,0)?(-2,0)
B.
椭圆C的长轴长为
C.
直线的方程为
D.
答案:BCD
12.
如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.
直线BD1⊥平面A1C1D
B.
三棱锥P﹣A1C1D的体积为定值
C.
异面直线AP与A1D所成角的取值范用是[45°,90°]
D.
直线C1P与平面A1C1D所成角的正弦值的最大值为
答案:ABD
三?填空题(本题包括4小题,每小题5分,共20分)
13.
设为单位向量,且,则________.
答案:
14.
已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡,若顾客甲只带了现金,顾客乙只用支付宝或微信付款,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中三种结账方式,则他们结账方式的可能情况有________种.
答案:20
15.
在三棱锥中,,,,.平面平面,若球是三棱锥的外接球,则球的半径为_________.
答案:4
16.
关于的方程在上有两个不相等的实根,则实数的取值范围______.
答案:
四?解答题(本题包括6小题.共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知数列的前n项和为,,设
(1)判断数列否为等差数列,并说明理由.
(2)求数列前n项和.
答案:(1)是,理由见解析;(2).
18.
已知的三个内角所对的边分别为,,,且满足.
(1)求角;
(2)若,且边上的中线的长为,求此时的面积.
答案:(1);(2)
19.
如图,在等腰梯形中,,,矩形所在平面垂直于平面,设平面与平面的交线为.
(1)求证:平面;
(2)若的长度为,求二面角的大小.
答案:(1)详见解析;(2).
20.
2020新年伊始爆发的新冠疫情让广大民众意识到健康的重要性,云南省全面开展爱国卫生7个专项行动及健康文明生活的6条新风尚行动,其中“科学健身”鼓励公众每天进行60分钟的体育锻炼.某社区从居民中随机抽取了若干名,统计他们的平均每天锻炼时间(单位:分钟/天),得到的数据如下表:(所有数据均在0~120分钟/天之间)
平均锻炼时间
人数
27
39
a
b
45
15
频率
009
0.13
0.38
c
0.15
0.05
(1)求,,的值;
(2)为了鼓励居民进行体育锻炼,该社区决定对运动时间不低于分钟的居民进行奖励,为使30%的人得到奖励,试估计的取值?
(3)在第(2)问的条件下,以频率作为概率,在该社区得到奖励的人中随机抽取4人,设这4人中日均锻炼时间不低于80分钟的人数为,求的分布列和数学期望.
答案:(1),;;(2);(3)分布列见解析;期望为.
21.
已知椭圆:,是坐标原点,,分别为椭圆的左、右焦点,点在椭圆上,过作的外角的平分线的垂线,垂足为,且.
(1)求椭圆的方程:
(2)设直线:与椭圆交于,两点,且直线,,的斜率之和为0(其中为坐标原点).
①求证:直线经过定点,并求出定点坐标:
②求面积的最大值.
答案:(1);(2)①证明见解析,;②.
22.
已知函数.
(1)讨论函数f(x)的单调性;
(2)当x>0时,恒成立,求实数a的取值范围.
答案:(1)见解析;(2)(﹣∞,e﹣1].
同课章节目录
