河北省深州市长江中学2020-2021学年高一下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 河北省深州市长江中学2020-2021学年高一下学期期中考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 12:39:46 | ||
图片预览


文档简介
长江中学2021学年度高一数学期中考试卷
一?单选题
1.
已知,其中为虚数单位,则复数在复平面内对应的点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2.
已知向量满足,且,则(
)
A.
B.
C.
D.
3.
如果向量,,那么
A
6
B.
5
C.
4
D.
3
4.
已知向量,,且,则实数等于
A.
B.
C.
D.
5.
复数则在复平面内,对应的点的坐标是(
)
A.
B.
C.
D.
6.
在四面体ABCD中,BCD是边长为2的等边三角形,ABD是以BD为斜边的等腰直角三角形,平面ABD⊥平面ABC,则四面体ABCD的外接球的表面积为(
)
A.
6π
B.
π
C.
8π
D.
2π
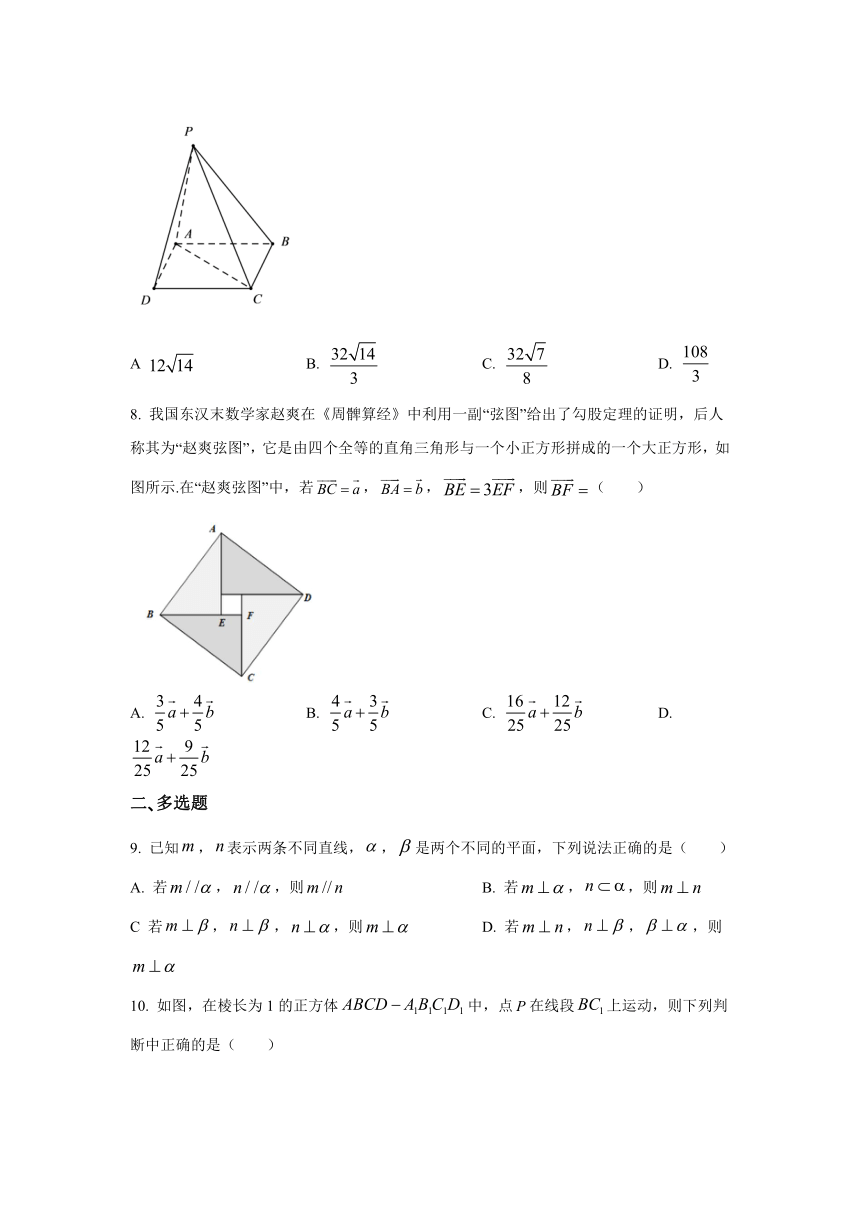
7.
如图,已知底面边长为的正四棱锥的侧棱长为若截面的面积为则正四棱锥的体积等于( )
A
B.
C.
D.
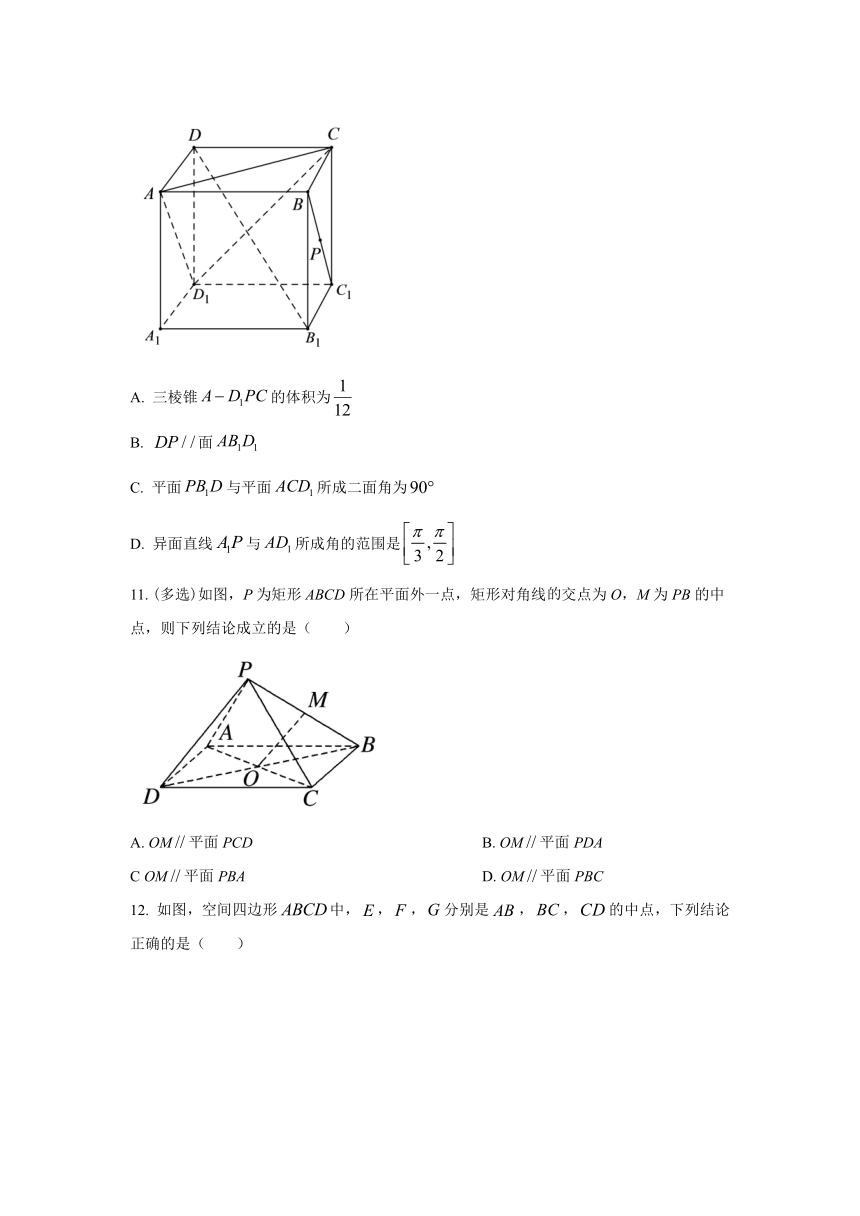
8.
我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若,,,则(
)
A.
B.
C.
D.
二?多选题
9.
已知,表示两条不同直线,,是两个不同的平面,下列说法正确的是(
)
A.
若,,则
B.
若,,则
C
若,,,则
D.
若,,,则
10.
如图,在棱长为1的正方体中,点在线段上运动,则下列判断中正确的是(
)
A.
三棱锥的体积为
B.
面
C.
平面与平面所成二面角为
D.
异面直线与所成角的范围是
11.
(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,则下列结论成立的是(
)
A.
OM平面PCD
B.
OM平面PDA
C
OM平面PBA
D.
OM平面PBC
12.
如图,空间四边形中,,,分别是,,的中点,下列结论正确的是(
)
A.
B.
平面
C.
平面
D.
,是一对相交直线
三?填空题
13.
设为单位向量,且,则______________.
14.
已知三棱锥的所有顶点都在球O的表面上,AD⊥平面ABC,AC=,BC=1,cos∠ACB=sin∠ACB,AD=3,则球O的表面积为________.
15.
已知正方体的所有顶点在一个球面上,若这个球的表面积为,则这个正方体的体积为___________.
16.
已知(i为虚数单位),则___________.
四?解答题
17.
已知的顶点坐标分别为,求的值.
18.
已知.
(1)若向量,求的值;
(2)若向量,证明:.
19.
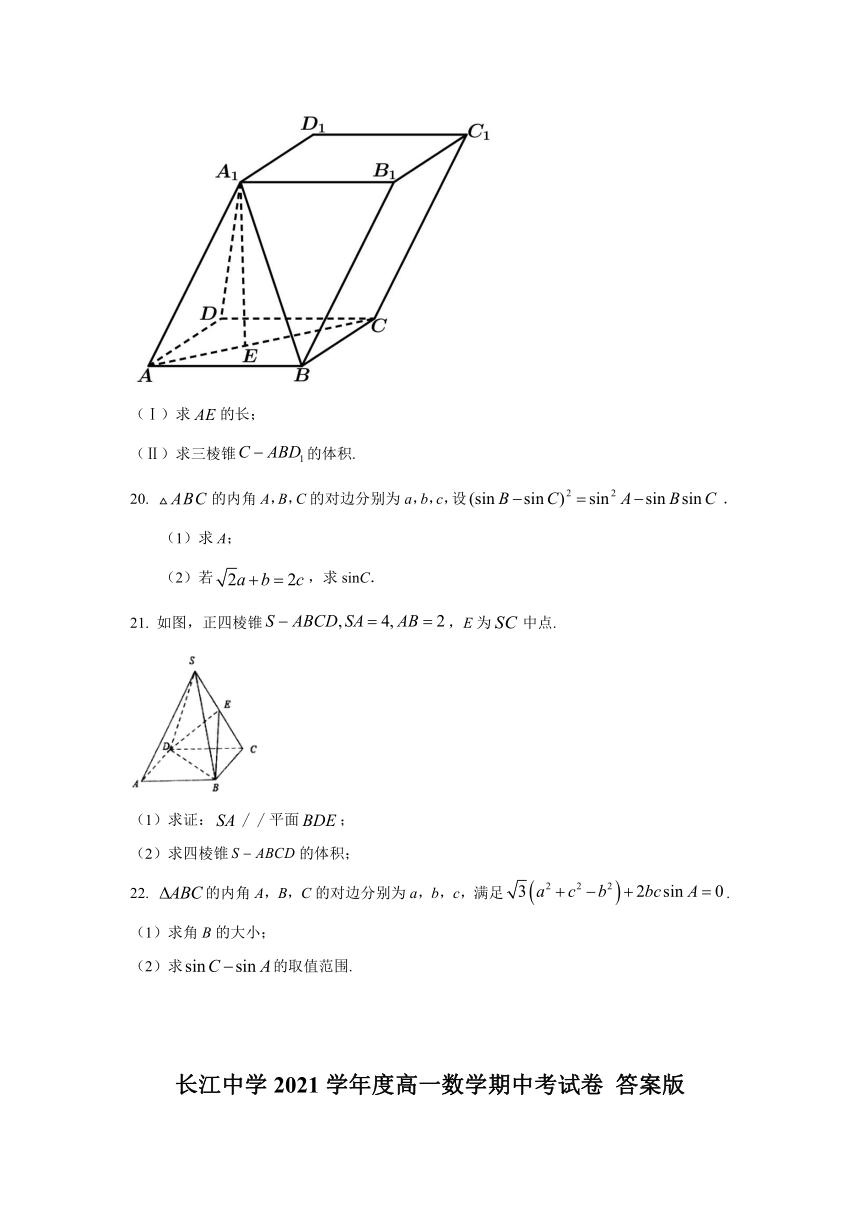
如图,在底面为菱形的四棱柱中,,,在底面内的射影为线段上一点.
(Ⅰ)求的长;
(Ⅱ)求三棱锥的体积.
20.
的内角A,B,C的对边分别为a,b,c,设.
(1)求A;
(2)若,求sinC.
21.
如图,正四棱锥,E为中点.
(1)求证:平面;
(2)求四棱锥的体积;
22.
的内角A,B,C的对边分别为a,b,c,满足.
(1)求角B的大小;
(2)求的取值范围.
长江中学2021学年度高一数学期中考试卷
答案版
一?单选题
1.
已知,其中为虚数单位,则复数在复平面内对应的点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
答案:D
2.
已知向量满足,且,则(
)
A.
B.
C.
D.
答案:B
3.
如果向量,,那么
A
6
B.
5
C.
4
D.
3
答案:B
4.
已知向量,,且,则实数等于
A.
B.
C.
D.
答案:C
5.
复数则在复平面内,对应的点的坐标是(
)
A.
B.
C.
D.
答案:B
6.
在四面体ABCD中,BCD是边长为2的等边三角形,ABD是以BD为斜边的等腰直角三角形,平面ABD⊥平面ABC,则四面体ABCD的外接球的表面积为(
)
A.
6π
B.
π
C.
8π
D.
2π
答案:A
7.
如图,已知底面边长为的正四棱锥的侧棱长为若截面的面积为则正四棱锥的体积等于( )
A
B.
C.
D.
答案:B
8.
我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若,,,则(
)
A.
B.
C.
D.
答案:C
二?多选题
9.
已知,表示两条不同直线,,是两个不同的平面,下列说法正确的是(
)
A.
若,,则
B.
若,,则
C
若,,,则
D.
若,,,则
答案:BC
10.
如图,在棱长为1的正方体中,点在线段上运动,则下列判断中正确的是(
)
A.
三棱锥的体积为
B.
面
C.
平面与平面所成二面角为
D.
异面直线与所成角的范围是
答案:BCD
11.
(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,则下列结论成立的是(
)
A.
OM平面PCD
B.
OM平面PDA
C
OM平面PBA
D.
OM平面PBC
答案:AB
12.
如图,空间四边形中,,,分别是,,的中点,下列结论正确的是(
)
A.
B.
平面
C.
平面
D.
,是一对相交直线
答案:BC
三?填空题
13.
设为单位向量,且,则______________.
答案:
14.
已知三棱锥的所有顶点都在球O的表面上,AD⊥平面ABC,AC=,BC=1,cos∠ACB=sin∠ACB,AD=3,则球O的表面积为________.
答案:
15.
已知正方体的所有顶点在一个球面上,若这个球的表面积为,则这个正方体的体积为___________.
答案:
16.
已知(i为虚数单位),则___________.
答案:
四?解答题
17.
已知的顶点坐标分别为,求的值.
答案:
18.
已知.
(1)若向量,求的值;
(2)若向量,证明:.
答案:(1);(2)详见解析.
19.
如图,在底面为菱形的四棱柱中,,,在底面内的射影为线段上一点.
(Ⅰ)求的长;
(Ⅱ)求三棱锥的体积.
答案:(Ⅰ);(Ⅱ).
20.
的内角A,B,C的对边分别为a,b,c,设.
(1)求A;
(2)若,求sinC.
答案:(1);(2).
21.
如图,正四棱锥,E为中点.
(1)求证:平面;
(2)求四棱锥的体积;
答案:(1)证明见解析;(2).
22.
的内角A,B,C的对边分别为a,b,c,满足.
(1)求角B的大小;
(2)求的取值范围.
答案:(1)(2)
一?单选题
1.
已知,其中为虚数单位,则复数在复平面内对应的点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2.
已知向量满足,且,则(
)
A.
B.
C.
D.
3.
如果向量,,那么
A
6
B.
5
C.
4
D.
3
4.
已知向量,,且,则实数等于
A.
B.
C.
D.
5.
复数则在复平面内,对应的点的坐标是(
)
A.
B.
C.
D.
6.
在四面体ABCD中,BCD是边长为2的等边三角形,ABD是以BD为斜边的等腰直角三角形,平面ABD⊥平面ABC,则四面体ABCD的外接球的表面积为(
)
A.
6π
B.
π
C.
8π
D.
2π
7.
如图,已知底面边长为的正四棱锥的侧棱长为若截面的面积为则正四棱锥的体积等于( )
A
B.
C.
D.
8.
我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若,,,则(
)
A.
B.
C.
D.
二?多选题
9.
已知,表示两条不同直线,,是两个不同的平面,下列说法正确的是(
)
A.
若,,则
B.
若,,则
C
若,,,则
D.
若,,,则
10.
如图,在棱长为1的正方体中,点在线段上运动,则下列判断中正确的是(
)
A.
三棱锥的体积为
B.
面
C.
平面与平面所成二面角为
D.
异面直线与所成角的范围是
11.
(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,则下列结论成立的是(
)
A.
OM平面PCD
B.
OM平面PDA
C
OM平面PBA
D.
OM平面PBC
12.
如图,空间四边形中,,,分别是,,的中点,下列结论正确的是(
)
A.
B.
平面
C.
平面
D.
,是一对相交直线
三?填空题
13.
设为单位向量,且,则______________.
14.
已知三棱锥的所有顶点都在球O的表面上,AD⊥平面ABC,AC=,BC=1,cos∠ACB=sin∠ACB,AD=3,则球O的表面积为________.
15.
已知正方体的所有顶点在一个球面上,若这个球的表面积为,则这个正方体的体积为___________.
16.
已知(i为虚数单位),则___________.
四?解答题
17.
已知的顶点坐标分别为,求的值.
18.
已知.
(1)若向量,求的值;
(2)若向量,证明:.
19.
如图,在底面为菱形的四棱柱中,,,在底面内的射影为线段上一点.
(Ⅰ)求的长;
(Ⅱ)求三棱锥的体积.
20.
的内角A,B,C的对边分别为a,b,c,设.
(1)求A;
(2)若,求sinC.
21.
如图,正四棱锥,E为中点.
(1)求证:平面;
(2)求四棱锥的体积;
22.
的内角A,B,C的对边分别为a,b,c,满足.
(1)求角B的大小;
(2)求的取值范围.
长江中学2021学年度高一数学期中考试卷
答案版
一?单选题
1.
已知,其中为虚数单位,则复数在复平面内对应的点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
答案:D
2.
已知向量满足,且,则(
)
A.
B.
C.
D.
答案:B
3.
如果向量,,那么
A
6
B.
5
C.
4
D.
3
答案:B
4.
已知向量,,且,则实数等于
A.
B.
C.
D.
答案:C
5.
复数则在复平面内,对应的点的坐标是(
)
A.
B.
C.
D.
答案:B
6.
在四面体ABCD中,BCD是边长为2的等边三角形,ABD是以BD为斜边的等腰直角三角形,平面ABD⊥平面ABC,则四面体ABCD的外接球的表面积为(
)
A.
6π
B.
π
C.
8π
D.
2π
答案:A
7.
如图,已知底面边长为的正四棱锥的侧棱长为若截面的面积为则正四棱锥的体积等于( )
A
B.
C.
D.
答案:B
8.
我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若,,,则(
)
A.
B.
C.
D.
答案:C
二?多选题
9.
已知,表示两条不同直线,,是两个不同的平面,下列说法正确的是(
)
A.
若,,则
B.
若,,则
C
若,,,则
D.
若,,,则
答案:BC
10.
如图,在棱长为1的正方体中,点在线段上运动,则下列判断中正确的是(
)
A.
三棱锥的体积为
B.
面
C.
平面与平面所成二面角为
D.
异面直线与所成角的范围是
答案:BCD
11.
(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,则下列结论成立的是(
)
A.
OM平面PCD
B.
OM平面PDA
C
OM平面PBA
D.
OM平面PBC
答案:AB
12.
如图,空间四边形中,,,分别是,,的中点,下列结论正确的是(
)
A.
B.
平面
C.
平面
D.
,是一对相交直线
答案:BC
三?填空题
13.
设为单位向量,且,则______________.
答案:
14.
已知三棱锥的所有顶点都在球O的表面上,AD⊥平面ABC,AC=,BC=1,cos∠ACB=sin∠ACB,AD=3,则球O的表面积为________.
答案:
15.
已知正方体的所有顶点在一个球面上,若这个球的表面积为,则这个正方体的体积为___________.
答案:
16.
已知(i为虚数单位),则___________.
答案:
四?解答题
17.
已知的顶点坐标分别为,求的值.
答案:
18.
已知.
(1)若向量,求的值;
(2)若向量,证明:.
答案:(1);(2)详见解析.
19.
如图,在底面为菱形的四棱柱中,,,在底面内的射影为线段上一点.
(Ⅰ)求的长;
(Ⅱ)求三棱锥的体积.
答案:(Ⅰ);(Ⅱ).
20.
的内角A,B,C的对边分别为a,b,c,设.
(1)求A;
(2)若,求sinC.
答案:(1);(2).
21.
如图,正四棱锥,E为中点.
(1)求证:平面;
(2)求四棱锥的体积;
答案:(1)证明见解析;(2).
22.
的内角A,B,C的对边分别为a,b,c,满足.
(1)求角B的大小;
(2)求的取值范围.
答案:(1)(2)
同课章节目录
