2021-2022学年苏科版初中数学七年级上册第1章我们与数学同行综合能力检测卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版初中数学七年级上册第1章我们与数学同行综合能力检测卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 468.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 11:54:10 | ||
图片预览

文档简介
第一章
我们与数学同行
单元测试
测试时间:45分钟
满分:100分
一、选择
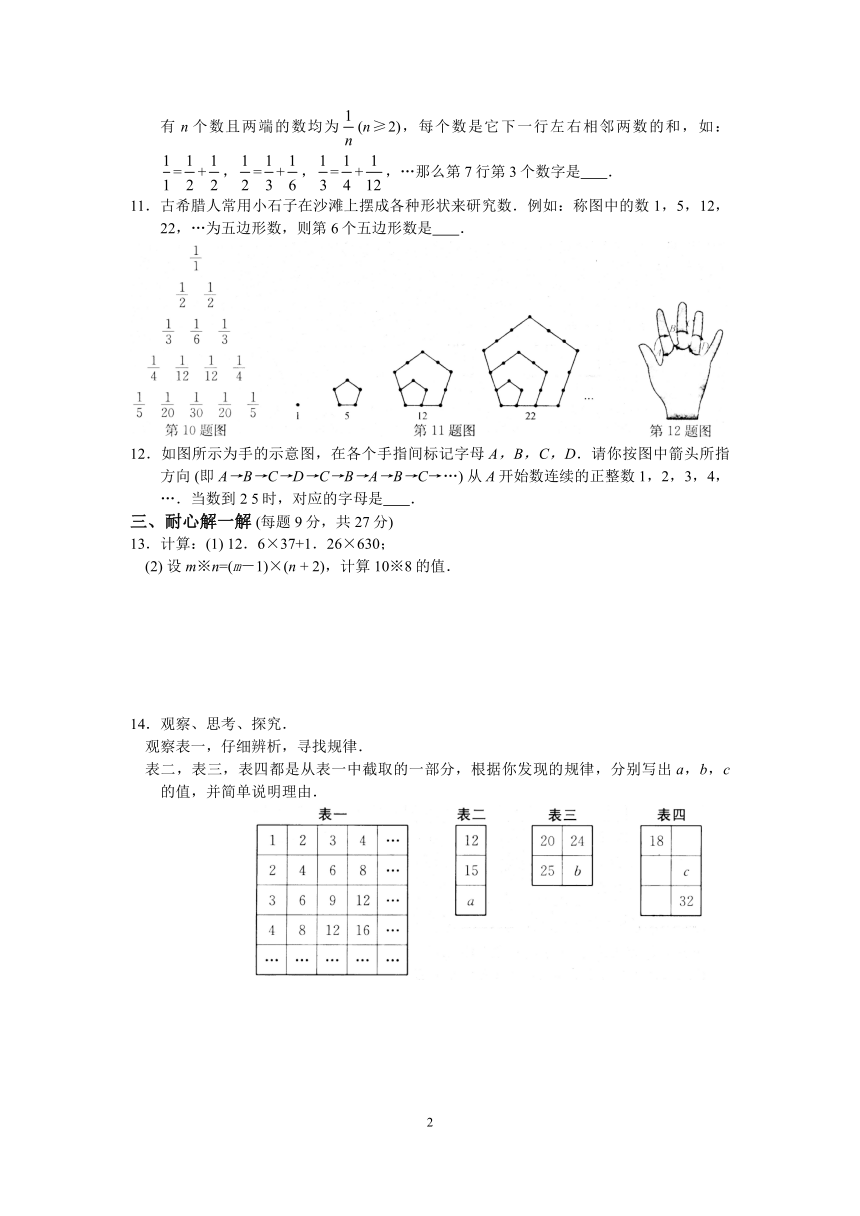
1.仔细观察下列图形,其中“与众不同”的一个是
(
)
2.一只青蛙在水井底,每天向上跃4米,又滑下3米,若井深9米,则它跃上这口井一共需
(
)
A.5天
B.6天
C.7天
D.9天
3.一张纸片,第1次把它撕成两个小片,以后每次将其中的一个小片撕成更小的两片,则第2
008次后共有纸片
(
)
A.2
008张
B.2
009张
C.4016张
D.20
080张
4.5名同学同台演出,在演出前,每两个同学握一次手,共握手的次数是
(
)
A.5
B.10
C.6
D.8
5.观察图中正方形四个顶点所标的数字规律,可知数2011应标在
(
)
A.第502个正方形的左下角
B.第502个正方形的右下角
C.第503个正方形的左上角
D.第503个正方形的右下角
6.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2011.个格子中的数为
(
)
A.3
B.2
C.0
D.-1
二、填空
7.找规律,在横线上填上适当的数:
(1)
1,4,8,13,
.(2)
1,,,,
.
8.小敏中午放学回家自己煮面条吃.有下面几道工序:①
洗锅盛水2分钟;②
洗菜3分钟;③
准备面条及佐料2分钟;④
用锅把水烧开7分钟;⑤
用烧开的水煮面条和菜要3分钟.以上各道工序,除④外,一次只能进行一道工序.小敏要将面条煮好,最少需要
分钟.
9.通过找出这组图形符号中所蕴含的内在规律,在空白处的横线上填上恰当的图形.
10.如图所示的数阵叫“莱布尼兹调和三角形”,他们是由正整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),每个数是它下一行左右相邻两数的和,如:=+,=+,=+,…那么第7行第3个数字是
.
11.古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22,…为五边形数,则第6个五边形数是
.
12.如图所示为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向
(即A→B→C→D→C→B→A→B→C→…)
从A开始数连续的正整数1,2,3,4,….当数到2
5时,对应的字母是
.
三、耐心解一解
(每题9分,共27分)
13.计算:(1)
12.6×37+1.26×630;
(2)
设m※n=(m-1)×(n
+
2),计算10※8的值.
14.观察、思考、探究.
观察表一,仔细辨析,寻找规律.
表二,表三,表四都是从表一中截取的一部分,根据你发现的规律,分别写出a,b,c
的值,并简单说明理由.
15.一张方桌周围可坐8人,试探索把桌子按下图排放时周围可坐人数的变化规律.
(1)
当顺排7张方桌时,周围可坐几人?
(2)
当顺排n张方桌时,周围可坐几人?
(3)
现有102人坐这种排列的桌子,每人只坐一个座位,至少要排多少张桌子?
16.我们把分子为1的分数叫做单位分数.如,,,….任何一个单位分数都可以拆分成两个不同的单位分数的和,如=十,=十,=十,….
(1)
根据上述式子,你会发现=十.请写出口,○所表示的数;
(2)
进一步思考,单位分数(n是不小于2的正整数)=十,请写出△,☆所表示的式子.
17.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.
(1)
如上图所示中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式,答:S=
.
(2)
请你再画出一些格点多边形,使这些多边形内部都有而且只有2个格点.
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=
.
(3)
请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?
18.(本题3分)
观察图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+…+120
=
.
参考答案
1.D
2.B
3.B
4.B
5.C
6.A
7.(1)
19
(2)
8.12
9.
10.
11.51
12.A
13.90
14.从表一中,可以发现如下的规律:第一列从1开始,相邻两数的差是1;第二列从2开始,相邻两数的差是2;第三列从3开始,相邻两数的差是3……第一行从1开始,相邻两数的差是1;第二行从2开始,相邻两数的差是2;第三行从3开始,相邻两数的差是3……我们也可以把这个规律理解为:每个数是它所在行数与列数的乘积.提示:18=1×18=18×1=2×9=9×2=3×6=6×3,对照另外一个已知数32,比18多一列多二行,可以确定c在第四列第七行,所以c=28.同理,a=18,b=30.
15.(1)
32
(2)
4n+4
(3)
25
16.(1)
口表示的数为6,○表示的数为30.
(2)
△表示的式子为n
+
1,
☆表示的式子为n
(n
+
1).
17.(1)
S=x;
(2)
S=x+1.(3)
S=x
+
n-1.
我们与数学同行
单元测试
测试时间:45分钟
满分:100分
一、选择
1.仔细观察下列图形,其中“与众不同”的一个是
(
)
2.一只青蛙在水井底,每天向上跃4米,又滑下3米,若井深9米,则它跃上这口井一共需
(
)
A.5天
B.6天
C.7天
D.9天
3.一张纸片,第1次把它撕成两个小片,以后每次将其中的一个小片撕成更小的两片,则第2
008次后共有纸片
(
)
A.2
008张
B.2
009张
C.4016张
D.20
080张
4.5名同学同台演出,在演出前,每两个同学握一次手,共握手的次数是
(
)
A.5
B.10
C.6
D.8
5.观察图中正方形四个顶点所标的数字规律,可知数2011应标在
(
)
A.第502个正方形的左下角
B.第502个正方形的右下角
C.第503个正方形的左上角
D.第503个正方形的右下角
6.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2011.个格子中的数为
(
)
A.3
B.2
C.0
D.-1
二、填空
7.找规律,在横线上填上适当的数:
(1)
1,4,8,13,
.(2)
1,,,,
.
8.小敏中午放学回家自己煮面条吃.有下面几道工序:①
洗锅盛水2分钟;②
洗菜3分钟;③
准备面条及佐料2分钟;④
用锅把水烧开7分钟;⑤
用烧开的水煮面条和菜要3分钟.以上各道工序,除④外,一次只能进行一道工序.小敏要将面条煮好,最少需要
分钟.
9.通过找出这组图形符号中所蕴含的内在规律,在空白处的横线上填上恰当的图形.
10.如图所示的数阵叫“莱布尼兹调和三角形”,他们是由正整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),每个数是它下一行左右相邻两数的和,如:=+,=+,=+,…那么第7行第3个数字是
.
11.古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22,…为五边形数,则第6个五边形数是
.
12.如图所示为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向
(即A→B→C→D→C→B→A→B→C→…)
从A开始数连续的正整数1,2,3,4,….当数到2
5时,对应的字母是
.
三、耐心解一解
(每题9分,共27分)
13.计算:(1)
12.6×37+1.26×630;
(2)
设m※n=(m-1)×(n
+
2),计算10※8的值.
14.观察、思考、探究.
观察表一,仔细辨析,寻找规律.
表二,表三,表四都是从表一中截取的一部分,根据你发现的规律,分别写出a,b,c
的值,并简单说明理由.
15.一张方桌周围可坐8人,试探索把桌子按下图排放时周围可坐人数的变化规律.
(1)
当顺排7张方桌时,周围可坐几人?
(2)
当顺排n张方桌时,周围可坐几人?
(3)
现有102人坐这种排列的桌子,每人只坐一个座位,至少要排多少张桌子?
16.我们把分子为1的分数叫做单位分数.如,,,….任何一个单位分数都可以拆分成两个不同的单位分数的和,如=十,=十,=十,….
(1)
根据上述式子,你会发现=十.请写出口,○所表示的数;
(2)
进一步思考,单位分数(n是不小于2的正整数)=十,请写出△,☆所表示的式子.
17.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.
(1)
如上图所示中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式,答:S=
.
(2)
请你再画出一些格点多边形,使这些多边形内部都有而且只有2个格点.
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=
.
(3)
请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?
18.(本题3分)
观察图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+…+120
=
.
参考答案
1.D
2.B
3.B
4.B
5.C
6.A
7.(1)
19
(2)
8.12
9.
10.
11.51
12.A
13.90
14.从表一中,可以发现如下的规律:第一列从1开始,相邻两数的差是1;第二列从2开始,相邻两数的差是2;第三列从3开始,相邻两数的差是3……第一行从1开始,相邻两数的差是1;第二行从2开始,相邻两数的差是2;第三行从3开始,相邻两数的差是3……我们也可以把这个规律理解为:每个数是它所在行数与列数的乘积.提示:18=1×18=18×1=2×9=9×2=3×6=6×3,对照另外一个已知数32,比18多一列多二行,可以确定c在第四列第七行,所以c=28.同理,a=18,b=30.
15.(1)
32
(2)
4n+4
(3)
25
16.(1)
口表示的数为6,○表示的数为30.
(2)
△表示的式子为n
+
1,
☆表示的式子为n
(n
+
1).
17.(1)
S=x;
(2)
S=x+1.(3)
S=x
+
n-1.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
