2021-2022学年苏科版八年级数学上册第一章全等三角形综合能力检测卷(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册第一章全等三角形综合能力检测卷(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 16:55:09 | ||
图片预览



文档简介
第1章 综合能力检测卷
时间:90分钟
满分:130分
一、选择题(每小题3分,共30分)
1.下列各组图形中不是全等图形的是
( )
A B C D
2.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的
( )
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
3.已知△ABC≌△DEF,∠A=70°,∠E=80°,则∠F的度数为
( )
A.30°
B.40°
C.50°
D.70°
4.如图,在△ABC和△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是
( )
A.∠B=∠E,BC=EF
B.BC=EF,AC=DF
C.∠A=∠D,∠B=∠E
D.∠A=∠D,BC=EF
5.如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是
( )
A.以点E为圆心,OE长为半径画弧
B.以点E为圆心,EF长为半径画弧
C.以点F为圆心,OE长为半径画弧
D.以点F为圆心,EF长为半径画弧
第4题图 第5题图 第6题图
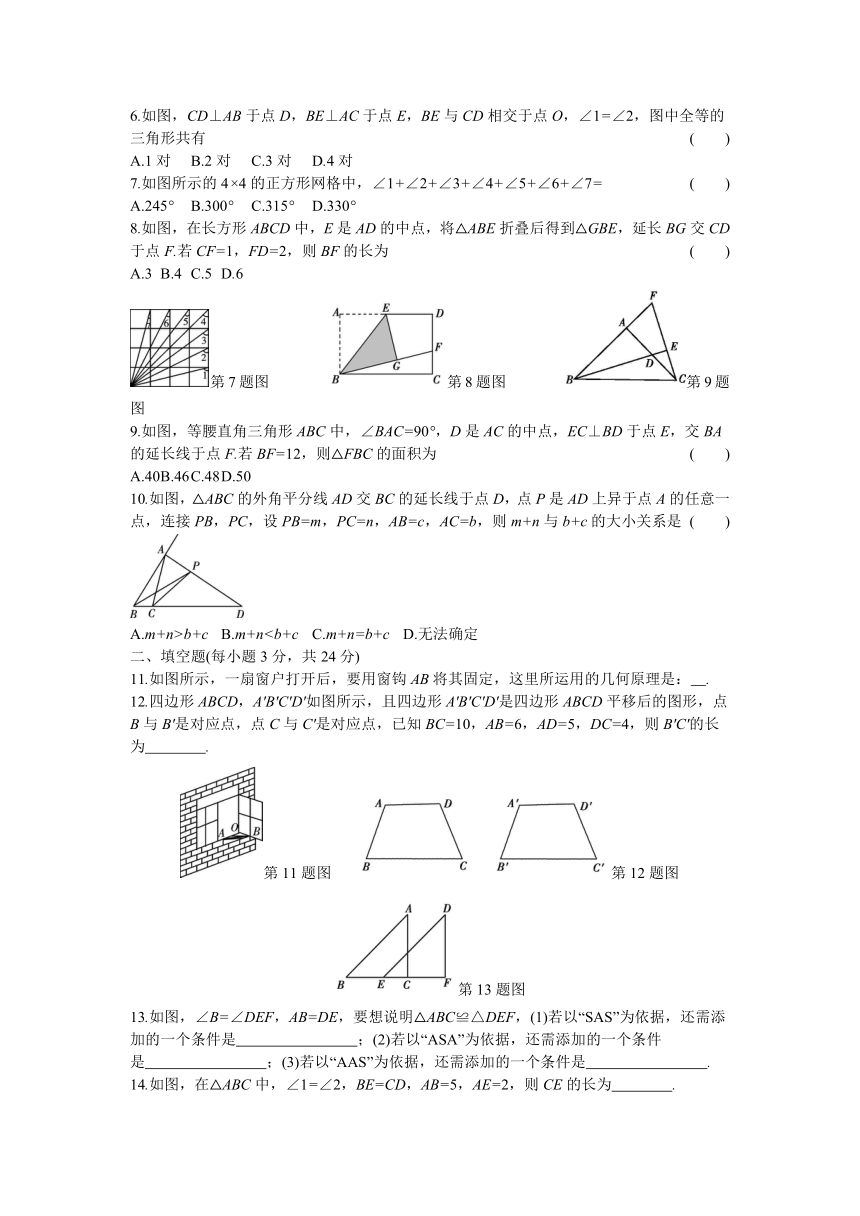
6.如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,∠1=∠2,图中全等的三角形共有
( )
A.1对
B.2对
C.3对
D.4对
7.如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
( )
A.245°
B.300°
C.315°
D.330°
8.如图,在长方形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BF的长为
( )
A.3
B.4
C.5
D.6
第7题图 第8题图 第9题图
9.如图,等腰直角三角形ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为
( )
A.40
B.46
C.48
D.50
10.如图,△ABC的外角平分线AD交BC的延长线于点D,点P是AD上异于点A的任意一点,连接PB,PC,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是
( )
A.m+n>b+c
B.m+nC.m+n=b+c
D.无法确定
二、填空题(每小题3分,共24分)
11.如图所示,一扇窗户打开后,要用窗钩AB将其固定,这里所运用的几何原理是: .?
12.四边形ABCD,A'B'C'D'如图所示,且四边形A'B'C'D'是四边形ABCD平移后的图形,点B与B'是对应点,点C与C'是对应点,已知BC=10,AB=6,AD=5,DC=4,则B'C'的长为 .?
第11题图 第12题图 第13题图
13.如图,∠B=∠DEF,AB=DE,要想说明△ABC≌△DEF,(1)若以“SAS”为依据,还需添加的一个条件是 ;(2)若以“ASA”为依据,还需添加的一个条件是 ;(3)若以“AAS”为依据,还需添加的一个条件是 .?
14.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE的长为 .?
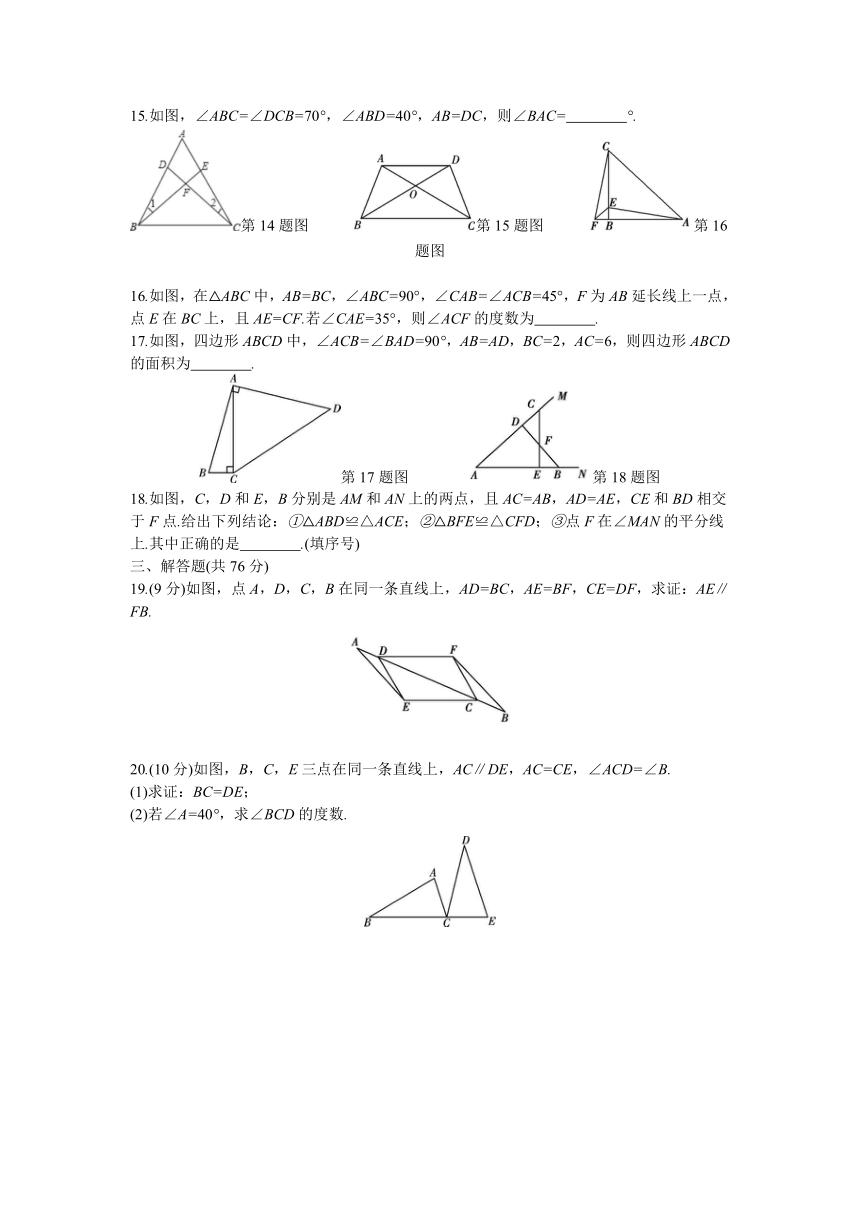
15.如图,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC= °.?
第14题图 第15题图 第16题图
16.如图,在△ABC中,AB=BC,∠ABC=90°,∠CAB=∠ACB=45°,F为AB延长线上一点,点E在BC上,且AE=CF.若∠CAE=35°,则∠ACF的度数为 .?
17.如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,则四边形ABCD的面积为 .?
第17题图 第18题图
18.如图,C,D和E,B分别是AM和AN上的两点,且AC=AB,AD=AE,CE和BD相交于F点.给出下列结论:①△ABD≌△ACE;②△BFE≌△CFD;③点F在∠MAN的平分线上.其中正确的是 .(填序号)?
三、解答题(共76分)
19.(9分)如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
20.(10分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE;
(2)若∠A=40°,求∠BCD的度数.
21.(9分)如图,BD⊥AC,CE⊥AB,BD与CE相交于点F,且BF=CF,连接AF,试判断∠BAF与∠CAF的大小关系,并说明理由.
22.(10分)如图,点B,F,C,E在一条直线l上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=14
m,BF=5
m,求FC的长度.
23.(12分)如图,已知点B,E,C,F在一条直线上,且点E,C三等分线段BF,AB=DF,AC=DE.
(1)求证:AC∥DE;
(2)连接BD,AF,试探究这两条线段的数量关系,并说明理由.
24.(12分)问题提出
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考
我们不妨将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
深入探究
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可得Rt△ABC≌Rt△DEF.?
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图2,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.请你用尺规在图3中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)对于(3),∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接填写结论:在△ABC与△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,若 ,则△ABC≌△DEF.?
25.(14分)如图,在△ABC中,∠BAD=∠DAC,DF⊥AB于F,DM⊥AC于M,AB=16
cm,AF=10
cm,AC=14
cm,动点E以2
cm/s的速度从A点向F点运动,同时动点G以1
cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t
s.
(1)求S△ABD∶S△ACD.
(2)求证:在运动过程中,无论t取何值,都有S△AED=2S△DGC.
(3)当t取何值时,△DFE与△DMG全等?
第1章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
A
D
B
D
C
C
C
A
11.三角形的稳定性 12.10 13.(1)BC=EF;(2)∠A=∠D;(3)∠ACB=∠F(答案不唯一) 14.3 15.80 16.55°
17.24 18.①②③
1.B
2.A 【解析】 添加条件AB=CD可证明AC=BD,由AE∥FD,得∠A=∠D,且已知AE=DF,根据“SAS”可得△EAC≌△FDB.故选A.
3.A 【解析】 ∵△ABC≌△DEF,∠A=70°,∴∠D=∠A=70°.又∵∠E=80°,∴∠F=180°-∠D-∠E=30°.故选A.
4.D 【解析】 因为没有“ASS”或“SSA”,所以D选项不能证明这两个三角形全等.故选D.
5.B
6.D 【解析】 因为CD⊥AB,BE⊥AC,所以∠OEA=∠ODA=90°,又因为∠1=∠2,AO=AO,所以△ADO≌△AEO(AAS),所以OD=OE,AD=AE,从而可以证明△DOB≌△EOC(ASA),△ADC≌△AEB(ASA),在此基础上易证△AOB≌△AOC(AAS),故有4对三角形全等.故选D.
7.C 【解析】 由题图可知∠4=×90°=45°,∠1和∠7所在的三角形全等,且∠1+∠7=90°.同理∠2+∠6=90°,∠3+∠5=90°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315°.故选C.
8.C 【解析】 由题意知AB=CD=CF+FD=3,由折叠的性质可知,△ABE≌△GBE,所以BG=AB=3,AE=EG=ED,连接EF,在Rt△EGF和Rt△EDF中,EG=ED,EF=EF,所以Rt△EGF≌Rt△EDF(HL),所以GF=DF=2,所以BF=BG+GF=3+2=5.故选C.
9.C 【解析】 因为CE⊥BD,所以∠BEF=90°,因为∠BAC=90°,所以∠CAF=90°,所以∠CAF=∠BAD=90°,∠ABD+∠F=90°,∠ACF+∠F=90°,所以∠ABD=∠ACF.在△ABD和△ACF中,所以△ABD≌△ACF(ASA),所以AD=AF.因为AB=AC,D为AC的中点,所以AB=AC=2AD=2AF.因为BF=AB+AF=3AF=12,所以AF=4,所以AB=AC=2AF=8,所以△FBC的面积为BF·AC=×12×8=48.故选C.
10.A 【解析】 如图,在BA的延长线上取点E,使AE=AC,连接EP,∵AD是△BAC的外角平分线,∴∠CAD=∠EAD.在△ACP和△AEP中,
∴△ACP≌△AEP(SAS),∴PE=PC.在△PBE中,PB+PE>AB+AE,∵PB=m,PC=n,AB=c,AC=b,∴m+n>b+c.故选A.
11.三角形的稳定性
12.10 【解析】 因为全等图形能完全重合,所以全等图形的对应边、对应角都相等,因为B'C'对应BC,所以B'C'=BC=10.
13.(1)BC=EF;(2)∠A=∠D;(3)∠ACB=∠F(答案不唯一)
14.3 【解析】 在△ABE和△ACD中,所以△ABE≌△ACD(AAS),所以AC=AB=5,所以CE=AC-AE=5-2=3.
15.80 【解析】 在△ABC和△DCB中,∴△ABC≌△DCB(SAS),∴∠ACB=∠DBC.∵∠ABD=40°,∠ABC=70°,∴∠DBC=30°,∴∠ACB=30°.∵∠ABC+∠ACB+∠BAC=180°,∴∠BAC=80°.
16.55° 【解析】 ∵∠CAB=∠ACB=45°,∴∠BAE=∠CAB-∠CAE=45°-35°=10°.在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL),∴∠BCF=∠BAE=10°,∴∠ACF=∠BCF+∠ACB=45°+10°=55°.
17.24 【解析】 如图,过点A作EA⊥AC,过点D作DE⊥AE于点E,∵∠BAC+∠CAD=90°,∠DAE+∠CAD=90°,∴∠BAC=∠DAE.在△ABC和△ADE中,∴△ABC≌△ADE(AAS),∴AE=AC,DE=BC,∴S四边形ABCD=S四边形ACDE.∵S四边形ACDE=(AC+DE)·AE=×8×6=24,∴四边形ABCD的面积为24.
18.①②③ 【解析】 在△ABD和△ACE中,AD=AE,∠A=∠A,AB=AC,∴△ABD≌△ACE(SAS),∴①正确;由①得∠AEC=∠ADB,∴∠FEB=∠FDC.∵AC=AB,AD=AE,∴DC=EB.在△BFE和△CFD中,∠BFE=∠CFD,∠FEB=∠FDC,EB=DC,∴△BFE≌△CFD(AAS),∴②正确;由②得DF=FE,连接AF,在△AFD和△AFE中,AD=AE,DF=EF,AF=AF,∴△AFD≌△AFE(SSS),∴∠DAF=∠EAF,∴点F在∠MAN的平分线上,∴③正确.故正确的序号为①②③.
19.【解析】 ∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE∥BF.
20.【解析】 (1)∵AC∥DE,
∴∠ACB=∠DEC,∠ACD=∠D,
∵∠ACD=∠B,∴∠D=∠B.
在△ABC和△CDE中,
∴△ABC≌△CDE(AAS),∴BC=DE.
(2)由(1)知△ABC≌△CDE,
∴∠DCE=∠A=40°,
∴∠BCD=180°-40°=140°.
21.【解析】 ∠BAF=∠CAF.理由如下:
∵BD⊥AC,CE⊥AB,
∴∠FEB=∠FDC=90°.
又∵∠EFB=∠DFC,BF=CF,
∴△BEF≌△CDF(AAS).
∴FE=FD.
又∵FD⊥AC,FE⊥AB,AF=AF,
∴Rt△AEF≌Rt△ADF(HL).
∴∠FAE=∠FAD,即∠BAF=∠CAF.
本题综合考查了全等三角形的判定与性质,通过两次全等探索∠BAF与∠CAF的大小关系,在后面的学习中我们也可以用角平分线的性质定理进行证明.
22.【解析】 (1)∵AB∥DE,∴∠ABC=∠DEF.
∵AC∥DF,∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,∴BF=EC.
∵BE=14
m,BF=5
m,
∴FC=14-5-5=4(m).
23.【解析】 (1)∵点E,C三等分线段BF,
∴BC=EF=BF.
在△ABC和△DFE中,
∴△ABC≌△DFE(SSS).
∴∠ACB=∠DEF,∴AC∥DE.
(2)BD=AF.理由如下:
如图,∵△ABC≌△DFE,∴∠ABC=∠DFE.
又∵AB=DF,BF=FB,
∴△ABF≌△DFB(SAS),∴BD=AF.
24.【解析】 (1)HL
(2)如图,分别过点C,F作边AB,DE上的高CG,FH,其中G,H为垂足.
∵∠ABC,∠DEF都是钝角,
∴G,H分别在AB,DE的延长线上.
∵CG⊥AG,FH⊥DH,∴∠CGA=∠FHD=90°.
∵∠CBG=180°-∠ABC,∠FEH=∠180°-∠DEF,∠ABC=∠DEF,∴∠CBG=∠FEH.
在△BCG和△EFH中,
∵∠CGB=∠FHE,∠CBG=∠FEH,BC=EF,
∴△BCG≌△EFH(AAS),∴CG=FH.
又∵AC=DF,∴Rt△ACG≌Rt△DFH(HL).
∴∠A=∠D.
在△ABC和△DEF中,
∵∠ABC=∠DEF,∠A=∠D,AC=DF,
∴△ABC≌△DEF(AAS).
(3)如图,△DEF就是所求作的三角形,△DEF和△ABC不全等.
(4)∠B≥∠A(答案不唯一)
由(3)知以C为圆心,AC长为半径画弧时,当弧与边AB交于点A,B之间时,△DEF和△ABC不全等,当弧与边AB交于点B或没有交点时,△ABC≌△DEF.则当AC≥BC,即∠B≥∠A时,△ABC≌△DEF,故答案为∠B≥∠A.
25.【解析】 (1)∵DF⊥AB,DM⊥AC,∴∠DFA=∠DMA=90°,
又∵∠FAD=∠MAD,AD=AD,∴△FAD≌△MAD(AAS),∴DF=DM.
∵S△ABD=AB·DF,S△ACD=AC·DM,AB=16
cm,AC=14
cm,
∴S△ABD∶S△ACD=AB∶AC=8∶7.
(2)∵S△AED=AE·DF,S△DGC=CG·DM,DF=DM,
∴S△AED∶S△DGC=AE∶CG,
∵点E以2
cm/s的速度从A点向F点运动,同时点G以1
cm/s的速度从C点向A点运动,
∴AE∶CG=2∶1,∴S△AED=2S△DGC.
∴在运动过程中,无论t取何值,都有S△AED=2S△DGC.
(3)由(1)知Rt△ADF≌Rt△ADM,
∴AM=AF=10
cm.
∵点E以2
cm/s的速度从A点向F点运动,同时点G以1
cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,运动时间为t
s,
∴EF=AF-AE=(10-2t)cm,CG=t
cm(0①当G点在线段AM上时,MG=CG-(AC-AM)=(t-4)cm.
当EF=MG时,△DFE与△DMG全等,
则10-2t=t-4,解得
t=.
②当G在线段CM上时,MG=(4-t)cm,
当EF=MG时,△DFE与△DMG全等,
则10-2t=4-t,解得t=6(舍去).
∴当
t=时,△DFE
与△DMG
全等.
时间:90分钟
满分:130分
一、选择题(每小题3分,共30分)
1.下列各组图形中不是全等图形的是
( )
A B C D
2.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的
( )
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
3.已知△ABC≌△DEF,∠A=70°,∠E=80°,则∠F的度数为
( )
A.30°
B.40°
C.50°
D.70°
4.如图,在△ABC和△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是
( )
A.∠B=∠E,BC=EF
B.BC=EF,AC=DF
C.∠A=∠D,∠B=∠E
D.∠A=∠D,BC=EF
5.如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是
( )
A.以点E为圆心,OE长为半径画弧
B.以点E为圆心,EF长为半径画弧
C.以点F为圆心,OE长为半径画弧
D.以点F为圆心,EF长为半径画弧
第4题图 第5题图 第6题图
6.如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,∠1=∠2,图中全等的三角形共有
( )
A.1对
B.2对
C.3对
D.4对
7.如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
( )
A.245°
B.300°
C.315°
D.330°
8.如图,在长方形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BF的长为
( )
A.3
B.4
C.5
D.6
第7题图 第8题图 第9题图
9.如图,等腰直角三角形ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为
( )
A.40
B.46
C.48
D.50
10.如图,△ABC的外角平分线AD交BC的延长线于点D,点P是AD上异于点A的任意一点,连接PB,PC,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是
( )
A.m+n>b+c
B.m+n
D.无法确定
二、填空题(每小题3分,共24分)
11.如图所示,一扇窗户打开后,要用窗钩AB将其固定,这里所运用的几何原理是: .?
12.四边形ABCD,A'B'C'D'如图所示,且四边形A'B'C'D'是四边形ABCD平移后的图形,点B与B'是对应点,点C与C'是对应点,已知BC=10,AB=6,AD=5,DC=4,则B'C'的长为 .?
第11题图 第12题图 第13题图
13.如图,∠B=∠DEF,AB=DE,要想说明△ABC≌△DEF,(1)若以“SAS”为依据,还需添加的一个条件是 ;(2)若以“ASA”为依据,还需添加的一个条件是 ;(3)若以“AAS”为依据,还需添加的一个条件是 .?
14.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE的长为 .?
15.如图,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC= °.?
第14题图 第15题图 第16题图
16.如图,在△ABC中,AB=BC,∠ABC=90°,∠CAB=∠ACB=45°,F为AB延长线上一点,点E在BC上,且AE=CF.若∠CAE=35°,则∠ACF的度数为 .?
17.如图,四边形ABCD中,∠ACB=∠BAD=90°,AB=AD,BC=2,AC=6,则四边形ABCD的面积为 .?
第17题图 第18题图
18.如图,C,D和E,B分别是AM和AN上的两点,且AC=AB,AD=AE,CE和BD相交于F点.给出下列结论:①△ABD≌△ACE;②△BFE≌△CFD;③点F在∠MAN的平分线上.其中正确的是 .(填序号)?
三、解答题(共76分)
19.(9分)如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
20.(10分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE;
(2)若∠A=40°,求∠BCD的度数.
21.(9分)如图,BD⊥AC,CE⊥AB,BD与CE相交于点F,且BF=CF,连接AF,试判断∠BAF与∠CAF的大小关系,并说明理由.
22.(10分)如图,点B,F,C,E在一条直线l上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=14
m,BF=5
m,求FC的长度.
23.(12分)如图,已知点B,E,C,F在一条直线上,且点E,C三等分线段BF,AB=DF,AC=DE.
(1)求证:AC∥DE;
(2)连接BD,AF,试探究这两条线段的数量关系,并说明理由.
24.(12分)问题提出
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考
我们不妨将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
深入探究
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可得Rt△ABC≌Rt△DEF.?
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图2,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.请你用尺规在图3中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)对于(3),∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接填写结论:在△ABC与△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,若 ,则△ABC≌△DEF.?
25.(14分)如图,在△ABC中,∠BAD=∠DAC,DF⊥AB于F,DM⊥AC于M,AB=16
cm,AF=10
cm,AC=14
cm,动点E以2
cm/s的速度从A点向F点运动,同时动点G以1
cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t
s.
(1)求S△ABD∶S△ACD.
(2)求证:在运动过程中,无论t取何值,都有S△AED=2S△DGC.
(3)当t取何值时,△DFE与△DMG全等?
第1章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
A
D
B
D
C
C
C
A
11.三角形的稳定性 12.10 13.(1)BC=EF;(2)∠A=∠D;(3)∠ACB=∠F(答案不唯一) 14.3 15.80 16.55°
17.24 18.①②③
1.B
2.A 【解析】 添加条件AB=CD可证明AC=BD,由AE∥FD,得∠A=∠D,且已知AE=DF,根据“SAS”可得△EAC≌△FDB.故选A.
3.A 【解析】 ∵△ABC≌△DEF,∠A=70°,∴∠D=∠A=70°.又∵∠E=80°,∴∠F=180°-∠D-∠E=30°.故选A.
4.D 【解析】 因为没有“ASS”或“SSA”,所以D选项不能证明这两个三角形全等.故选D.
5.B
6.D 【解析】 因为CD⊥AB,BE⊥AC,所以∠OEA=∠ODA=90°,又因为∠1=∠2,AO=AO,所以△ADO≌△AEO(AAS),所以OD=OE,AD=AE,从而可以证明△DOB≌△EOC(ASA),△ADC≌△AEB(ASA),在此基础上易证△AOB≌△AOC(AAS),故有4对三角形全等.故选D.
7.C 【解析】 由题图可知∠4=×90°=45°,∠1和∠7所在的三角形全等,且∠1+∠7=90°.同理∠2+∠6=90°,∠3+∠5=90°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315°.故选C.
8.C 【解析】 由题意知AB=CD=CF+FD=3,由折叠的性质可知,△ABE≌△GBE,所以BG=AB=3,AE=EG=ED,连接EF,在Rt△EGF和Rt△EDF中,EG=ED,EF=EF,所以Rt△EGF≌Rt△EDF(HL),所以GF=DF=2,所以BF=BG+GF=3+2=5.故选C.
9.C 【解析】 因为CE⊥BD,所以∠BEF=90°,因为∠BAC=90°,所以∠CAF=90°,所以∠CAF=∠BAD=90°,∠ABD+∠F=90°,∠ACF+∠F=90°,所以∠ABD=∠ACF.在△ABD和△ACF中,所以△ABD≌△ACF(ASA),所以AD=AF.因为AB=AC,D为AC的中点,所以AB=AC=2AD=2AF.因为BF=AB+AF=3AF=12,所以AF=4,所以AB=AC=2AF=8,所以△FBC的面积为BF·AC=×12×8=48.故选C.
10.A 【解析】 如图,在BA的延长线上取点E,使AE=AC,连接EP,∵AD是△BAC的外角平分线,∴∠CAD=∠EAD.在△ACP和△AEP中,
∴△ACP≌△AEP(SAS),∴PE=PC.在△PBE中,PB+PE>AB+AE,∵PB=m,PC=n,AB=c,AC=b,∴m+n>b+c.故选A.
11.三角形的稳定性
12.10 【解析】 因为全等图形能完全重合,所以全等图形的对应边、对应角都相等,因为B'C'对应BC,所以B'C'=BC=10.
13.(1)BC=EF;(2)∠A=∠D;(3)∠ACB=∠F(答案不唯一)
14.3 【解析】 在△ABE和△ACD中,所以△ABE≌△ACD(AAS),所以AC=AB=5,所以CE=AC-AE=5-2=3.
15.80 【解析】 在△ABC和△DCB中,∴△ABC≌△DCB(SAS),∴∠ACB=∠DBC.∵∠ABD=40°,∠ABC=70°,∴∠DBC=30°,∴∠ACB=30°.∵∠ABC+∠ACB+∠BAC=180°,∴∠BAC=80°.
16.55° 【解析】 ∵∠CAB=∠ACB=45°,∴∠BAE=∠CAB-∠CAE=45°-35°=10°.在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL),∴∠BCF=∠BAE=10°,∴∠ACF=∠BCF+∠ACB=45°+10°=55°.
17.24 【解析】 如图,过点A作EA⊥AC,过点D作DE⊥AE于点E,∵∠BAC+∠CAD=90°,∠DAE+∠CAD=90°,∴∠BAC=∠DAE.在△ABC和△ADE中,∴△ABC≌△ADE(AAS),∴AE=AC,DE=BC,∴S四边形ABCD=S四边形ACDE.∵S四边形ACDE=(AC+DE)·AE=×8×6=24,∴四边形ABCD的面积为24.
18.①②③ 【解析】 在△ABD和△ACE中,AD=AE,∠A=∠A,AB=AC,∴△ABD≌△ACE(SAS),∴①正确;由①得∠AEC=∠ADB,∴∠FEB=∠FDC.∵AC=AB,AD=AE,∴DC=EB.在△BFE和△CFD中,∠BFE=∠CFD,∠FEB=∠FDC,EB=DC,∴△BFE≌△CFD(AAS),∴②正确;由②得DF=FE,连接AF,在△AFD和△AFE中,AD=AE,DF=EF,AF=AF,∴△AFD≌△AFE(SSS),∴∠DAF=∠EAF,∴点F在∠MAN的平分线上,∴③正确.故正确的序号为①②③.
19.【解析】 ∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE∥BF.
20.【解析】 (1)∵AC∥DE,
∴∠ACB=∠DEC,∠ACD=∠D,
∵∠ACD=∠B,∴∠D=∠B.
在△ABC和△CDE中,
∴△ABC≌△CDE(AAS),∴BC=DE.
(2)由(1)知△ABC≌△CDE,
∴∠DCE=∠A=40°,
∴∠BCD=180°-40°=140°.
21.【解析】 ∠BAF=∠CAF.理由如下:
∵BD⊥AC,CE⊥AB,
∴∠FEB=∠FDC=90°.
又∵∠EFB=∠DFC,BF=CF,
∴△BEF≌△CDF(AAS).
∴FE=FD.
又∵FD⊥AC,FE⊥AB,AF=AF,
∴Rt△AEF≌Rt△ADF(HL).
∴∠FAE=∠FAD,即∠BAF=∠CAF.
本题综合考查了全等三角形的判定与性质,通过两次全等探索∠BAF与∠CAF的大小关系,在后面的学习中我们也可以用角平分线的性质定理进行证明.
22.【解析】 (1)∵AB∥DE,∴∠ABC=∠DEF.
∵AC∥DF,∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,∴BF=EC.
∵BE=14
m,BF=5
m,
∴FC=14-5-5=4(m).
23.【解析】 (1)∵点E,C三等分线段BF,
∴BC=EF=BF.
在△ABC和△DFE中,
∴△ABC≌△DFE(SSS).
∴∠ACB=∠DEF,∴AC∥DE.
(2)BD=AF.理由如下:
如图,∵△ABC≌△DFE,∴∠ABC=∠DFE.
又∵AB=DF,BF=FB,
∴△ABF≌△DFB(SAS),∴BD=AF.
24.【解析】 (1)HL
(2)如图,分别过点C,F作边AB,DE上的高CG,FH,其中G,H为垂足.
∵∠ABC,∠DEF都是钝角,
∴G,H分别在AB,DE的延长线上.
∵CG⊥AG,FH⊥DH,∴∠CGA=∠FHD=90°.
∵∠CBG=180°-∠ABC,∠FEH=∠180°-∠DEF,∠ABC=∠DEF,∴∠CBG=∠FEH.
在△BCG和△EFH中,
∵∠CGB=∠FHE,∠CBG=∠FEH,BC=EF,
∴△BCG≌△EFH(AAS),∴CG=FH.
又∵AC=DF,∴Rt△ACG≌Rt△DFH(HL).
∴∠A=∠D.
在△ABC和△DEF中,
∵∠ABC=∠DEF,∠A=∠D,AC=DF,
∴△ABC≌△DEF(AAS).
(3)如图,△DEF就是所求作的三角形,△DEF和△ABC不全等.
(4)∠B≥∠A(答案不唯一)
由(3)知以C为圆心,AC长为半径画弧时,当弧与边AB交于点A,B之间时,△DEF和△ABC不全等,当弧与边AB交于点B或没有交点时,△ABC≌△DEF.则当AC≥BC,即∠B≥∠A时,△ABC≌△DEF,故答案为∠B≥∠A.
25.【解析】 (1)∵DF⊥AB,DM⊥AC,∴∠DFA=∠DMA=90°,
又∵∠FAD=∠MAD,AD=AD,∴△FAD≌△MAD(AAS),∴DF=DM.
∵S△ABD=AB·DF,S△ACD=AC·DM,AB=16
cm,AC=14
cm,
∴S△ABD∶S△ACD=AB∶AC=8∶7.
(2)∵S△AED=AE·DF,S△DGC=CG·DM,DF=DM,
∴S△AED∶S△DGC=AE∶CG,
∵点E以2
cm/s的速度从A点向F点运动,同时点G以1
cm/s的速度从C点向A点运动,
∴AE∶CG=2∶1,∴S△AED=2S△DGC.
∴在运动过程中,无论t取何值,都有S△AED=2S△DGC.
(3)由(1)知Rt△ADF≌Rt△ADM,
∴AM=AF=10
cm.
∵点E以2
cm/s的速度从A点向F点运动,同时点G以1
cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,运动时间为t
s,
∴EF=AF-AE=(10-2t)cm,CG=t
cm(0
当EF=MG时,△DFE与△DMG全等,
则10-2t=t-4,解得
t=.
②当G在线段CM上时,MG=(4-t)cm,
当EF=MG时,△DFE与△DMG全等,
则10-2t=4-t,解得t=6(舍去).
∴当
t=时,△DFE
与△DMG
全等.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
