1.3正方形的性质 课后培优 2021-2022学年北师大版数学九年级上册(Word版含解析)
文档属性
| 名称 | 1.3正方形的性质 课后培优 2021-2022学年北师大版数学九年级上册(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 658.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 19:09:52 | ||
图片预览


文档简介
正方形的性质
一、单选题
1.正方形具有而菱形不具有的性质是( )
A.对角线互相平行
B.每一条对角线平分一组对角
C.对角线相等
D.对边相等
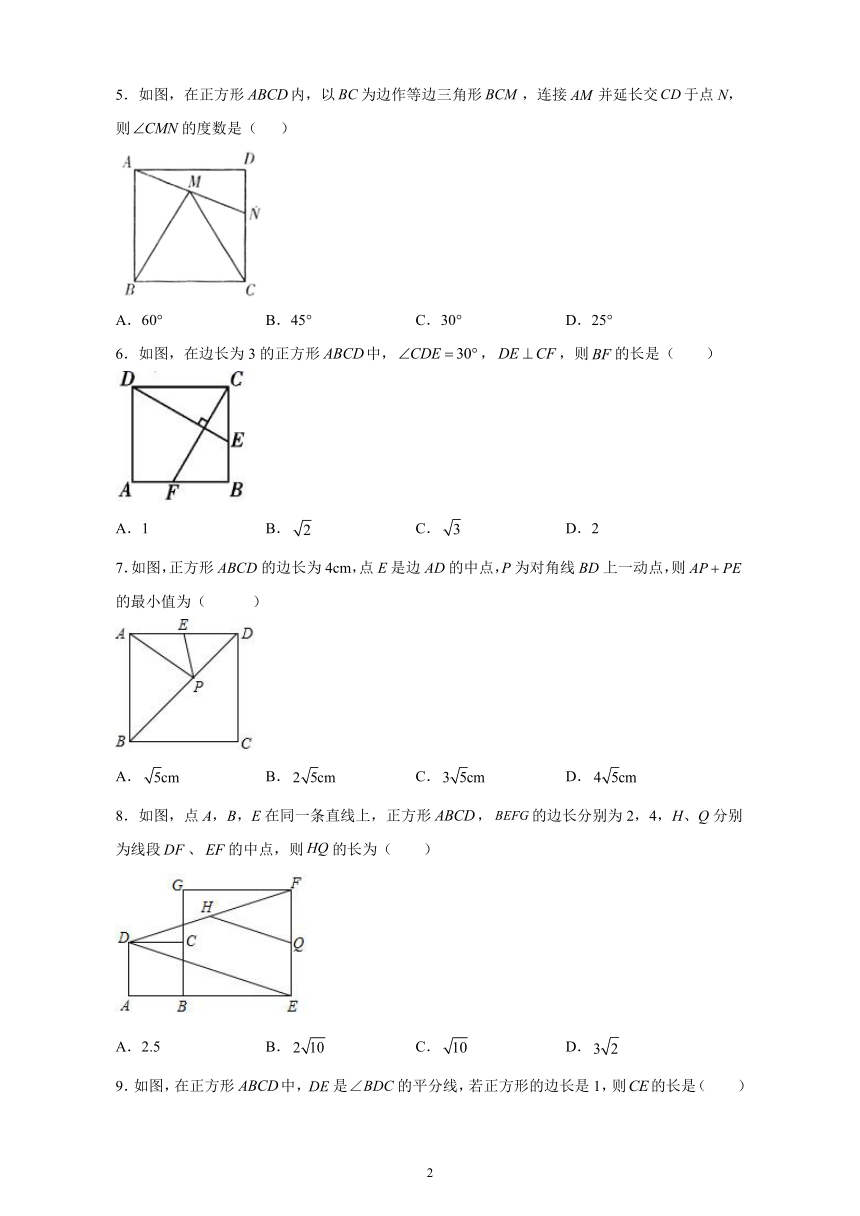
2.如图,正方形ABCD中,E、F是对角线BD上的两点,BD=12,BE=DF=8,则四边形AECF的面积为( )
A.24
B.12
C.4
D.2
3.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小
B.保持不变
C.一直变大
D.一直变小
4.如图,以边长为4的正方形的中心为端点,引两条互相垂直的射线,分别与正方形的边交于、两点,则线段的最小值是(
)
A.
B.2
C.
D.4
5.如图,在正方形内,以为边作等边三角形,连接并延长交于点N,则的度数是(
)
A.60°
B.45°
C.30°
D.25°
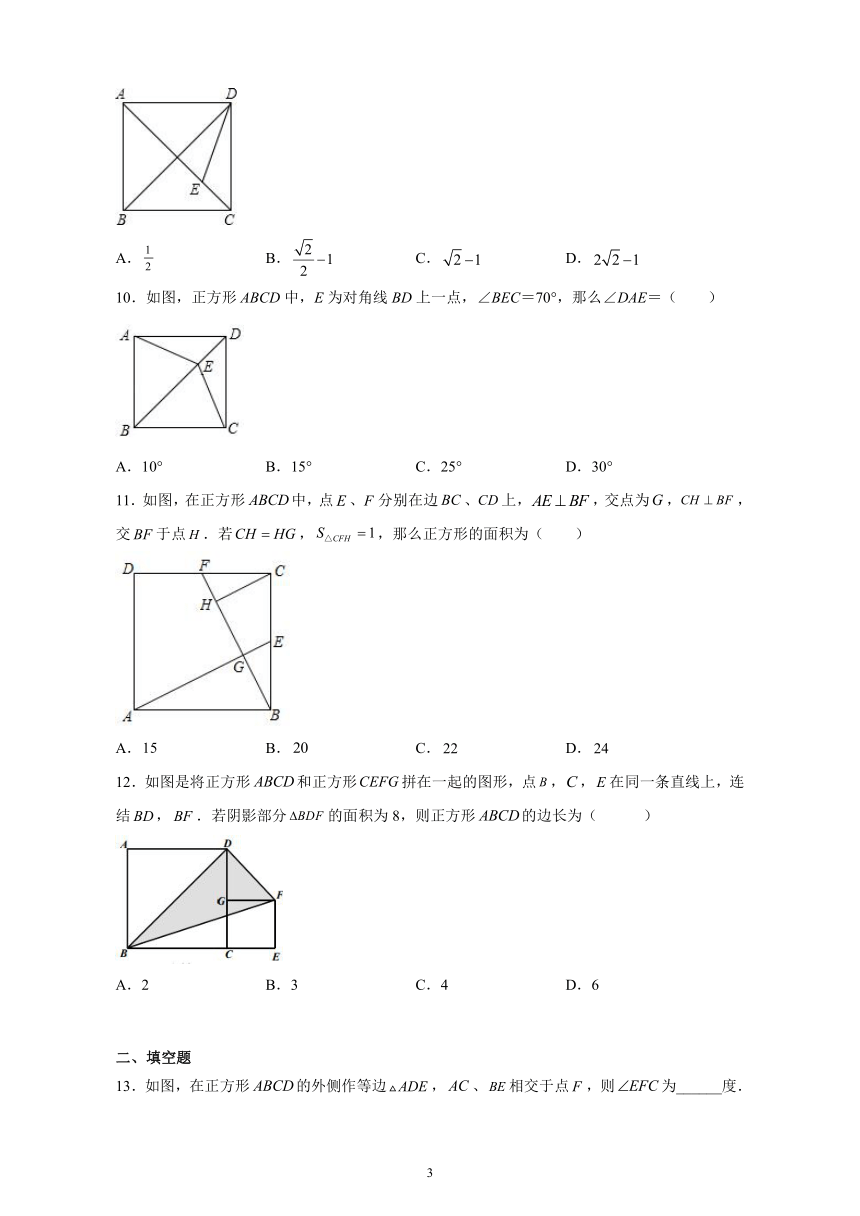
6.如图,在边长为3的正方形中,,,则的长是(
)
A.1
B.
C.
D.2
7.如图,正方形ABCD的边长为4cm,点E是边AD的中点,P为对角线BD上一动点,则的最小值为(
)
A.
B.
C.
D.
8.如图,点A,B,E在同一条直线上,正方形,的边长分别为2,4,H、Q分别为线段、的中点,则的长为(
)
A.2.5
B.
C.
D.
9.如图,在正方形中,是的平分线,若正方形的边长是1,则的长是(
)
A.
B.
C.
D.
10.如图,正方形ABCD中,E为对角线BD上一点,∠BEC=70°,那么∠DAE=(
)
A.10°
B.15°
C.25°
D.30°
11.如图,在正方形中,点、分别在边、上,,交点为,,交于点.若,,那么正方形的面积为(
)
A.
B.
C.
D.
12.如图是将正方形和正方形拼在一起的图形,点,,在同一条直线上,连结,.若阴影部分的面积为8,则正方形的边长为(
)
A.2
B.3
C.4
D.6
二、填空题
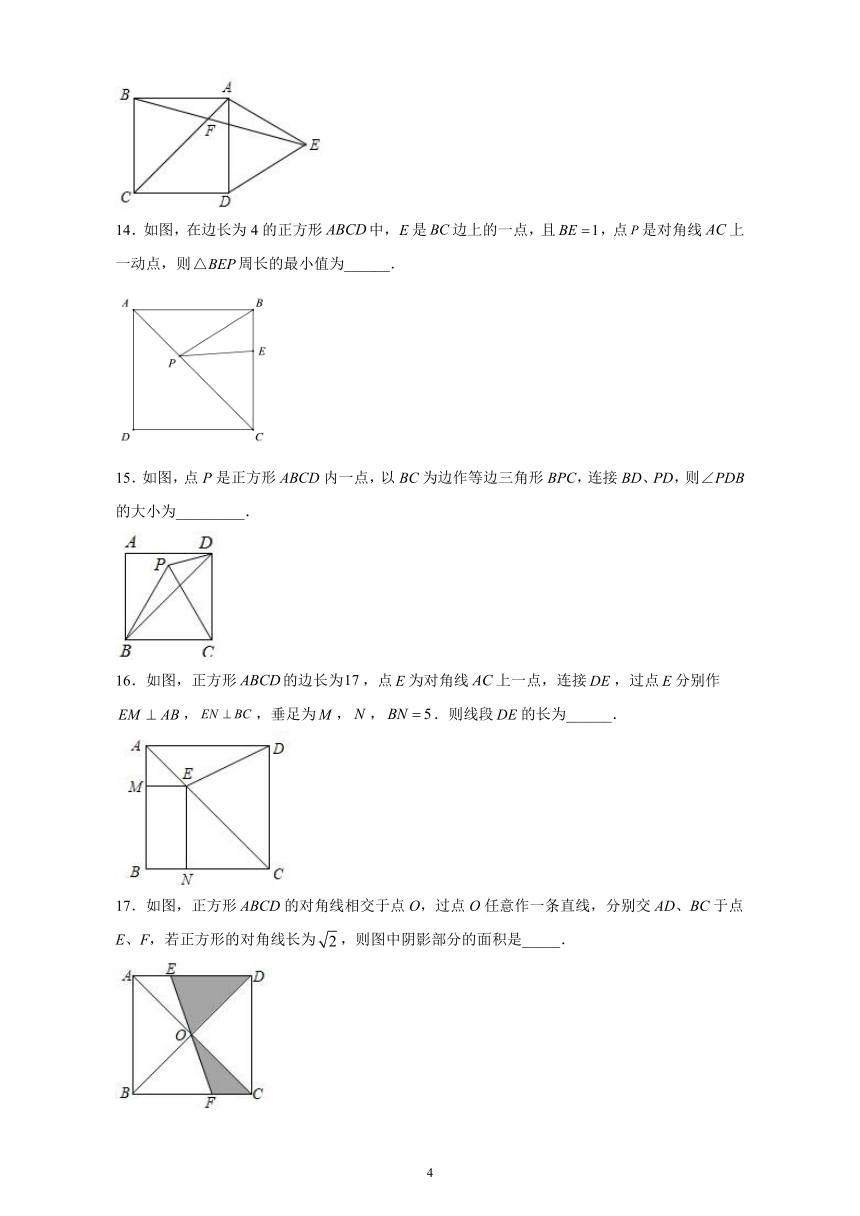
13.如图,在正方形的外侧作等边,、相交于点,则为______度.
14.如图,在边长为4的正方形中,是边上的一点,且,点是对角线上一动点,则周长的最小值为______.
15.如图,点P是正方形ABCD内一点,以BC为边作等边三角形BPC,连接BD、PD,则∠PDB的大小为_________.
16.如图,正方形的边长为,点为对角线上一点,连接,过点分别作,,垂足为,,.则线段的长为______.
17.如图,正方形ABCD的对角线相交于点O,过点O任意作一条直线,分别交AD、BC于点E、F,若正方形的对角线长为,则图中阴影部分的面积是_____.
三、解答题
18.如图所示,正方形ABCD中,AC,BD交于点O.BD=10,点E,F是BD上的两点,BE=DF=2.求四边形AECF的周长.
19.如图,是正方形的对角线,是直线上一点.
(1)若点在边上,,垂足是,且.求证:;
(2)若,连接,求的度数.
20.如图,已知点A在BG上,四边形ABCD与四边形DEFG都为正方形,其面积分别是7cm2和11cm2:
(1)求AG的长;
(2)求△CDE的面积.
21.如图,点P为正方形ABCD的对角转AC上一动点,过点P作PE⊥PB交射线DC于点E.
(1)如图1,当点E在边CD上时,求证:PB=PE;
(2)如图2,当点E在DC的延长线上时,探求线段PA、PC、CE的数量关系并加以证明;
(3)如图3,在(1)的条件下,连接BE交AC于点F,若正方形ABCD的边长为4,当点E为CD的中点,则PF= (请直接写出结果).
参考答案
1.C
解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:C.
2.A
解:连接AC,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,AC=BD=12,
∴AO=CO=BO=DO,
∵BE=DF=8,
∴BF=DE=BD-BE=4,
∴OE=OF,EF=DF-DE=4,
∴四边形AECF是菱形,
∴菱形AECF的面积=AC?EF=×12×4=24,
故选:A.
3.B
解:连接DE,
∵S△CDE=S矩形ECFG,
S△CDE=S正方形ABCD,
∴矩形ECFG与正方形ABCD的面积相等.即保持不变.
故选:B.
4.C
解:过点O作OG⊥AD于点G,如图
∵四边形ABCD是正方形,且对角线AC、BD相交于点O
∴OA=OB=OD
,∠OAF=∠OBE=45°,AC⊥BD
∴∠AOB=∠BOE+∠AOE=90°
∵OE⊥OF
∴∠AOE+∠AOF=90°
∴∠FOA=∠EOB
在△FOA和△EOB中
∴
△FOA≌△EOB(ASA)
∴OF=OE
∵OE⊥OF
∴由勾股定理得:
∴当OF最小时,EF最小
∵OG⊥AD
∴OF≥OG
即当OF与OG重合时,线段OF最小,最小值为OG的长,从而EF的最小值为
∵OA=OD,OG⊥AD
∴G点是AD的中点
∴OG=AD=2
∴
故选:C.
5.B
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BCM是等边三角形,
∴BM=BC,∠MBC=∠BMC=60°,
∴AB=BM,∠ABM=30°,
∴∠BAM=∠AMB,
又∵∠BAM+∠AMB+∠ABM=180°,
∴∠BAM=∠BMA=75°,
∴∠CMN=180°-∠CMB-∠BMA=45°,
故选B.
6.C
解:四边形是正方形,
,,
∵在中,,
,
设,则,
根据勾股定理得:,
即,
解得:(负值舍去),
,
,
,
,
,
,,
,
.
故选:.
7.B
解:如图,连接EC,PC,
∵AP+PE=PC+PE≥EC,
∴EC就是AP+PE的最小值,
∵正方形ABCD的边长为4cm,点E是边AD的中点,
∴CD=4cm,ED=2cm,
∴CE=,
∴AP+PE的最小值是2cm.
故选:B.
8.C
解:∵H、Q分别为线段DF、EF的中点,
∴HQ为三角形FDE的中位线,
∴,
∵点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为2,4,
∴AD=AB=2,BE=4,∠A=90°,
∴AE=AB+BE=6,
∴,
∴,
故选C.
9.C
解:∵四边形ABCD为正方形,
∴,
∴
∵AC,BC是正方形的对角线
∴
∵是的平分线,
∴
∴,
∴
∴
∴
故选C
10.C
解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,∠BCD=90°,
在△AED和△CED中,
,
∴△AED≌△CED(SAS),
∴∠DAE=∠ECD,
又∵∠BEC=70°,
∴∠BCE=180°﹣∠BEC﹣∠EBC=180°﹣70°﹣45°=65°,
∵∠BCD=∠BCE+∠ECD=90°,
∴∠ECD=90°﹣65°=25°,
∴∠DAE=25°,
故选:C.
11.B
解:四边形是正方形,
,,
,,
,,
,
,
,
在与中,
,
,
,
设,则,
,
,
设为,
,
在中,,
在中,,
,
解得:,
,
(舍负),
正方形的面积为.
故选:.
12.C
解:如图,连接CF,
∵四边形ABCD和四边形CGFE都是正方形,
∴∠BDC=45°,∠GCF=45°,
∴∠BDC=∠GCF,
∴BD∥CF,
∴S△BDF=S△BCD=8,
∴S△BDF=BC×BC÷2=8.
∴BC=4,
故选:C.
13.120.
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°,
∴∠EFC=180°﹣∠BFC=120°;
故答案为:120.
14.6
解:如图,作作关于的对称点,
正方形是轴对称图形,是它的一条对称轴,则在上,
,
,
当三点共线时候,最小,
四边形是正方形,
,
,
,
周长的最小值为的最小值,
即.
故答案为:6.
15.30°
解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,BC=CD,
∵△BPC是等边三角形,
∴∠PBC=∠BCP=∠BPC=60°,BP=PC=BC,
∵BC=CD,∠BCD=90°,
∴∠DBC=45°,
∴∠PBD=∠PBC﹣∠DBC=60°﹣45°=15°,
∵∠BCD=90°,∠BCP=60°,
∴∠PCD=90°﹣60°=30°,
∵PD=DC,
∴∠DPC=
,
∴∠PDB=180°﹣∠PBD﹣∠BPC﹣∠CPD=180°﹣15°﹣60°﹣75°=30°,
故答案为:30°.
16.
解:延长NE与AD交于F,
∵四边形ABCD是正方形,EM⊥AB,EN⊥BC,
∴∠MAE=45°,∠AME=∠BME=∠ENB=∠B=90°,
∴四边形BMEN是矩形,∠AEM=45°,
∴ME=AM=BN=5,NC=BC-BN=13
同理可以证明四边形NCDF是矩形,四边形AMEF是正方形,
∴DF=CN,EF=AM=5,
∴,
故答案为:13.
17.
解:在正方形ABCD中,
,
,
,
又∵
,
∴
,
∴
,
∴图中阴影部分的面积等于
,
∵正方形的对角线长为,
∴
,
,
∴图中阴影部分的面积等于
.
故答案为:.
18.4
解:∵四边形ABCD是正方形,
∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
∵BD=10,BE=DF=2,
∴OE=5﹣2=3,OC=5,
∴CE=,
∴菱形AECF的周长为4.
19.(1)见解析;(2)或
解:证明:(1)连接.
四边形是正方形,
.
,
,.
∴.
.
四边形是正方形,
.
.
.
(2)分两种情形:
①如图2,点在的延长线上
,
.
,
又,
.
②如图3,点在的延长线上,
,
又
.
由上①②可知的度数是或
20.(1)2;(2)
解:(1)∵四边形ABCD与四边形DEFG都为正方形,
其面积分别是7cm2和11cm2,
∴
,,
由勾股定理得:
(2)如图,延长
过作于
正方形
正方形
(负根舍去)
所以△CDE面积.
21.(1)见解析;(2)AP﹣PC=EC.证明见解析;(3).
解:(1)证明:如图1,连接PD.
∵四边形ABCD是正方形,
∴CB=CD,∠PCB=∠PCD=45°,
在△PCB和△PCD中,
,
∴△PCB≌△PCD(SAS),
∴PB=PD,∠CBP=∠CDP,
∵PE⊥PB,
∴∠BPE=∠BCE=90°,
∴∠CBP+∠CEP=180°,
∵∠CEP+∠PED=180°,
∴∠PED=∠CBP,
∴∠PED=∠CDP,
∴PE=PD,
∴PB=PE;
(2)解:结论:AP﹣PC=EC.理由如下:
如图2,过点P作PT⊥PC交BC于T,过点T作TH⊥BC交AC于H,过点H作HK⊥AB于K,设PE交BC于点O.
∵∠ECO=∠BPO=90°,∠EOC=∠BOP,
∴∠E=∠PBT,
∵∠BPE=∠TPC=90°,
∵∠BPT=∠EPC,
∵∠PCE=∠PTC=45°,
∴PT=PC,
在△BPT和△EPC中,
,
∴△BPT≌△EPC(AAS),
∴BT=EC,
∵HT⊥BC,
∴∠TCH=∠THC=45°,
∴CT=TH,
∵TP⊥CH,
∴PC=PH,
∵HK⊥AB,
∴∠HKB=∠KBT=⊥HTB=90°,
∴四边形BTHK是矩形,
∴HK=BT=EC,
∵∠AKH=90°,∠KAH=45°,
∴AH=KH=EC,
∵PA﹣PC=PA﹣PH=AH,
∴PA﹣PC=EC;
(3)解:如图3中,过点P作PL⊥BE于L,过点F作FQ⊥CD于Q,FJ⊥BC于J.
∵BC=CD=4,CE=ED=2,∠BCE=90°,
∴BE===2,
∵△BPE是等腰直角三角形,PL⊥BE,
∴BL=EL=,
∴PL=BE=,
∵FC平分∠BCE,FQ⊥CD,FJ⊥BC,
∴FQ=FJ,
∵===,
∴EF=BE=,
∴FL=LE﹣EF=﹣=,
∴PF===.
一、单选题
1.正方形具有而菱形不具有的性质是( )
A.对角线互相平行
B.每一条对角线平分一组对角
C.对角线相等
D.对边相等
2.如图,正方形ABCD中,E、F是对角线BD上的两点,BD=12,BE=DF=8,则四边形AECF的面积为( )
A.24
B.12
C.4
D.2
3.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小
B.保持不变
C.一直变大
D.一直变小
4.如图,以边长为4的正方形的中心为端点,引两条互相垂直的射线,分别与正方形的边交于、两点,则线段的最小值是(
)
A.
B.2
C.
D.4
5.如图,在正方形内,以为边作等边三角形,连接并延长交于点N,则的度数是(
)
A.60°
B.45°
C.30°
D.25°
6.如图,在边长为3的正方形中,,,则的长是(
)
A.1
B.
C.
D.2
7.如图,正方形ABCD的边长为4cm,点E是边AD的中点,P为对角线BD上一动点,则的最小值为(
)
A.
B.
C.
D.
8.如图,点A,B,E在同一条直线上,正方形,的边长分别为2,4,H、Q分别为线段、的中点,则的长为(
)
A.2.5
B.
C.
D.
9.如图,在正方形中,是的平分线,若正方形的边长是1,则的长是(
)
A.
B.
C.
D.
10.如图,正方形ABCD中,E为对角线BD上一点,∠BEC=70°,那么∠DAE=(
)
A.10°
B.15°
C.25°
D.30°
11.如图,在正方形中,点、分别在边、上,,交点为,,交于点.若,,那么正方形的面积为(
)
A.
B.
C.
D.
12.如图是将正方形和正方形拼在一起的图形,点,,在同一条直线上,连结,.若阴影部分的面积为8,则正方形的边长为(
)
A.2
B.3
C.4
D.6
二、填空题
13.如图,在正方形的外侧作等边,、相交于点,则为______度.
14.如图,在边长为4的正方形中,是边上的一点,且,点是对角线上一动点,则周长的最小值为______.
15.如图,点P是正方形ABCD内一点,以BC为边作等边三角形BPC,连接BD、PD,则∠PDB的大小为_________.
16.如图,正方形的边长为,点为对角线上一点,连接,过点分别作,,垂足为,,.则线段的长为______.
17.如图,正方形ABCD的对角线相交于点O,过点O任意作一条直线,分别交AD、BC于点E、F,若正方形的对角线长为,则图中阴影部分的面积是_____.
三、解答题
18.如图所示,正方形ABCD中,AC,BD交于点O.BD=10,点E,F是BD上的两点,BE=DF=2.求四边形AECF的周长.
19.如图,是正方形的对角线,是直线上一点.
(1)若点在边上,,垂足是,且.求证:;
(2)若,连接,求的度数.
20.如图,已知点A在BG上,四边形ABCD与四边形DEFG都为正方形,其面积分别是7cm2和11cm2:
(1)求AG的长;
(2)求△CDE的面积.
21.如图,点P为正方形ABCD的对角转AC上一动点,过点P作PE⊥PB交射线DC于点E.
(1)如图1,当点E在边CD上时,求证:PB=PE;
(2)如图2,当点E在DC的延长线上时,探求线段PA、PC、CE的数量关系并加以证明;
(3)如图3,在(1)的条件下,连接BE交AC于点F,若正方形ABCD的边长为4,当点E为CD的中点,则PF= (请直接写出结果).
参考答案
1.C
解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选:C.
2.A
解:连接AC,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,AC=BD=12,
∴AO=CO=BO=DO,
∵BE=DF=8,
∴BF=DE=BD-BE=4,
∴OE=OF,EF=DF-DE=4,
∴四边形AECF是菱形,
∴菱形AECF的面积=AC?EF=×12×4=24,
故选:A.
3.B
解:连接DE,
∵S△CDE=S矩形ECFG,
S△CDE=S正方形ABCD,
∴矩形ECFG与正方形ABCD的面积相等.即保持不变.
故选:B.
4.C
解:过点O作OG⊥AD于点G,如图
∵四边形ABCD是正方形,且对角线AC、BD相交于点O
∴OA=OB=OD
,∠OAF=∠OBE=45°,AC⊥BD
∴∠AOB=∠BOE+∠AOE=90°
∵OE⊥OF
∴∠AOE+∠AOF=90°
∴∠FOA=∠EOB
在△FOA和△EOB中
∴
△FOA≌△EOB(ASA)
∴OF=OE
∵OE⊥OF
∴由勾股定理得:
∴当OF最小时,EF最小
∵OG⊥AD
∴OF≥OG
即当OF与OG重合时,线段OF最小,最小值为OG的长,从而EF的最小值为
∵OA=OD,OG⊥AD
∴G点是AD的中点
∴OG=AD=2
∴
故选:C.
5.B
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BCM是等边三角形,
∴BM=BC,∠MBC=∠BMC=60°,
∴AB=BM,∠ABM=30°,
∴∠BAM=∠AMB,
又∵∠BAM+∠AMB+∠ABM=180°,
∴∠BAM=∠BMA=75°,
∴∠CMN=180°-∠CMB-∠BMA=45°,
故选B.
6.C
解:四边形是正方形,
,,
∵在中,,
,
设,则,
根据勾股定理得:,
即,
解得:(负值舍去),
,
,
,
,
,
,,
,
.
故选:.
7.B
解:如图,连接EC,PC,
∵AP+PE=PC+PE≥EC,
∴EC就是AP+PE的最小值,
∵正方形ABCD的边长为4cm,点E是边AD的中点,
∴CD=4cm,ED=2cm,
∴CE=,
∴AP+PE的最小值是2cm.
故选:B.
8.C
解:∵H、Q分别为线段DF、EF的中点,
∴HQ为三角形FDE的中位线,
∴,
∵点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为2,4,
∴AD=AB=2,BE=4,∠A=90°,
∴AE=AB+BE=6,
∴,
∴,
故选C.
9.C
解:∵四边形ABCD为正方形,
∴,
∴
∵AC,BC是正方形的对角线
∴
∵是的平分线,
∴
∴,
∴
∴
∴
故选C
10.C
解:∵四边形ABCD是正方形,
∴∠ADE=∠CDE=∠EBC=45°,AD=CD,∠BCD=90°,
在△AED和△CED中,
,
∴△AED≌△CED(SAS),
∴∠DAE=∠ECD,
又∵∠BEC=70°,
∴∠BCE=180°﹣∠BEC﹣∠EBC=180°﹣70°﹣45°=65°,
∵∠BCD=∠BCE+∠ECD=90°,
∴∠ECD=90°﹣65°=25°,
∴∠DAE=25°,
故选:C.
11.B
解:四边形是正方形,
,,
,,
,,
,
,
,
在与中,
,
,
,
设,则,
,
,
设为,
,
在中,,
在中,,
,
解得:,
,
(舍负),
正方形的面积为.
故选:.
12.C
解:如图,连接CF,
∵四边形ABCD和四边形CGFE都是正方形,
∴∠BDC=45°,∠GCF=45°,
∴∠BDC=∠GCF,
∴BD∥CF,
∴S△BDF=S△BCD=8,
∴S△BDF=BC×BC÷2=8.
∴BC=4,
故选:C.
13.120.
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°,
∴∠EFC=180°﹣∠BFC=120°;
故答案为:120.
14.6
解:如图,作作关于的对称点,
正方形是轴对称图形,是它的一条对称轴,则在上,
,
,
当三点共线时候,最小,
四边形是正方形,
,
,
,
周长的最小值为的最小值,
即.
故答案为:6.
15.30°
解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,BC=CD,
∵△BPC是等边三角形,
∴∠PBC=∠BCP=∠BPC=60°,BP=PC=BC,
∵BC=CD,∠BCD=90°,
∴∠DBC=45°,
∴∠PBD=∠PBC﹣∠DBC=60°﹣45°=15°,
∵∠BCD=90°,∠BCP=60°,
∴∠PCD=90°﹣60°=30°,
∵PD=DC,
∴∠DPC=
,
∴∠PDB=180°﹣∠PBD﹣∠BPC﹣∠CPD=180°﹣15°﹣60°﹣75°=30°,
故答案为:30°.
16.
解:延长NE与AD交于F,
∵四边形ABCD是正方形,EM⊥AB,EN⊥BC,
∴∠MAE=45°,∠AME=∠BME=∠ENB=∠B=90°,
∴四边形BMEN是矩形,∠AEM=45°,
∴ME=AM=BN=5,NC=BC-BN=13
同理可以证明四边形NCDF是矩形,四边形AMEF是正方形,
∴DF=CN,EF=AM=5,
∴,
故答案为:13.
17.
解:在正方形ABCD中,
,
,
,
又∵
,
∴
,
∴
,
∴图中阴影部分的面积等于
,
∵正方形的对角线长为,
∴
,
,
∴图中阴影部分的面积等于
.
故答案为:.
18.4
解:∵四边形ABCD是正方形,
∴OD=OB,OA=OC,BD⊥AC,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
∵BD=10,BE=DF=2,
∴OE=5﹣2=3,OC=5,
∴CE=,
∴菱形AECF的周长为4.
19.(1)见解析;(2)或
解:证明:(1)连接.
四边形是正方形,
.
,
,.
∴.
.
四边形是正方形,
.
.
.
(2)分两种情形:
①如图2,点在的延长线上
,
.
,
又,
.
②如图3,点在的延长线上,
,
又
.
由上①②可知的度数是或
20.(1)2;(2)
解:(1)∵四边形ABCD与四边形DEFG都为正方形,
其面积分别是7cm2和11cm2,
∴
,,
由勾股定理得:
(2)如图,延长
过作于
正方形
正方形
(负根舍去)
所以△CDE面积.
21.(1)见解析;(2)AP﹣PC=EC.证明见解析;(3).
解:(1)证明:如图1,连接PD.
∵四边形ABCD是正方形,
∴CB=CD,∠PCB=∠PCD=45°,
在△PCB和△PCD中,
,
∴△PCB≌△PCD(SAS),
∴PB=PD,∠CBP=∠CDP,
∵PE⊥PB,
∴∠BPE=∠BCE=90°,
∴∠CBP+∠CEP=180°,
∵∠CEP+∠PED=180°,
∴∠PED=∠CBP,
∴∠PED=∠CDP,
∴PE=PD,
∴PB=PE;
(2)解:结论:AP﹣PC=EC.理由如下:
如图2,过点P作PT⊥PC交BC于T,过点T作TH⊥BC交AC于H,过点H作HK⊥AB于K,设PE交BC于点O.
∵∠ECO=∠BPO=90°,∠EOC=∠BOP,
∴∠E=∠PBT,
∵∠BPE=∠TPC=90°,
∵∠BPT=∠EPC,
∵∠PCE=∠PTC=45°,
∴PT=PC,
在△BPT和△EPC中,
,
∴△BPT≌△EPC(AAS),
∴BT=EC,
∵HT⊥BC,
∴∠TCH=∠THC=45°,
∴CT=TH,
∵TP⊥CH,
∴PC=PH,
∵HK⊥AB,
∴∠HKB=∠KBT=⊥HTB=90°,
∴四边形BTHK是矩形,
∴HK=BT=EC,
∵∠AKH=90°,∠KAH=45°,
∴AH=KH=EC,
∵PA﹣PC=PA﹣PH=AH,
∴PA﹣PC=EC;
(3)解:如图3中,过点P作PL⊥BE于L,过点F作FQ⊥CD于Q,FJ⊥BC于J.
∵BC=CD=4,CE=ED=2,∠BCE=90°,
∴BE===2,
∵△BPE是等腰直角三角形,PL⊥BE,
∴BL=EL=,
∴PL=BE=,
∵FC平分∠BCE,FQ⊥CD,FJ⊥BC,
∴FQ=FJ,
∵===,
∴EF=BE=,
∴FL=LE﹣EF=﹣=,
∴PF===.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
