1.4.2用空间向量研究距离、夹角问题(第1课时)课件——2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共17张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题(第1课时)课件——2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 11:01:58 | ||
图片预览



文档简介
(共17张PPT)
人教A版(2019)选择性必修第一册
第一章
空间向量与立体几何
1.4.2
用空间向量研究距离、夹角问题
(第1课时)
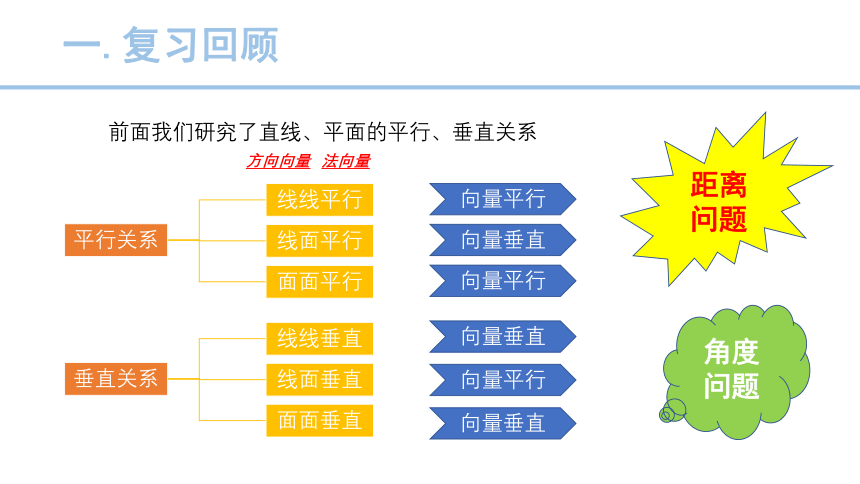
一.复习回顾
前面我们研究了直线、平面的平行、垂直关系
向量平行
向量垂直
向量平行
向量垂直
向量平行
向量垂直
距离问题
角度
问题
方向向量
法向量
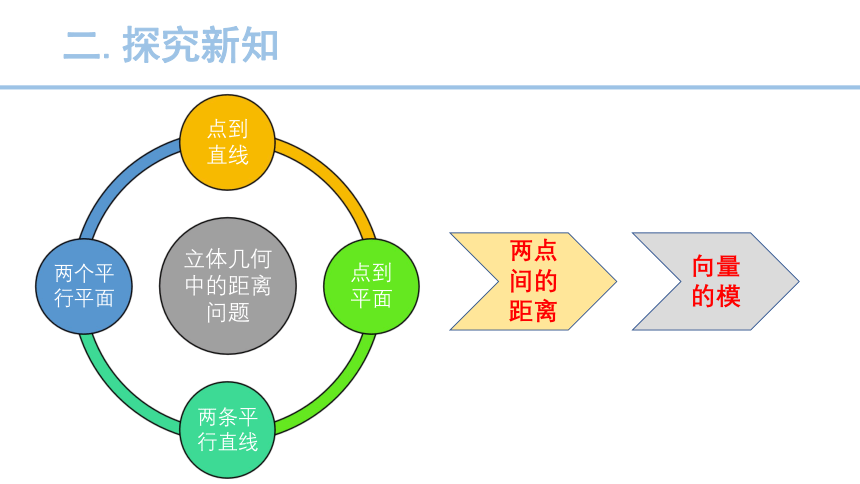
二.探究新知
两点间的距离
向量的模
l
A
u
Q
P
已知直线l的单位方向向量为u
,
A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
探究1
如图,直线l上的投影向量为则在直角三角形APQ
中,,∠
PAQ都是确定的.
设=a,则=(a·u)u,由勾股定理,得
PQ=
Q
l
A
P
M
l2
A
u
Q
P
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
思考
l1
自主探究,时间3分钟
设=a,则=(a·u)u,由勾股定理,得
PQ=
在l1上取定一点P,l2上取一点A
找l1或l2的方向向量u
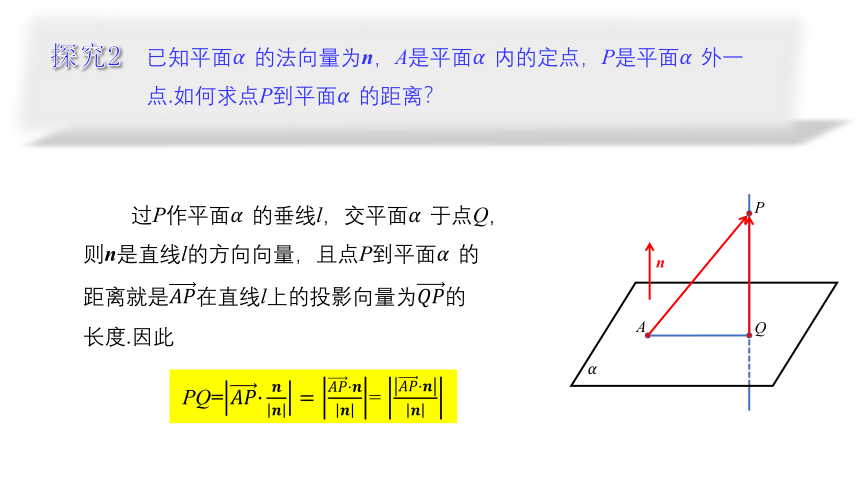
已知平面?的法向量为n,A是平面?内的定点,P是平面?外一点.如何求点P到平面?的距离?
探究2
n
过P作平面?的垂线l,交平面?于点Q,则n是直线l的方向向量,且点P到平面?的距离就是直线l上的投影向量为长度.因此
P
A
PQ=
=
Q
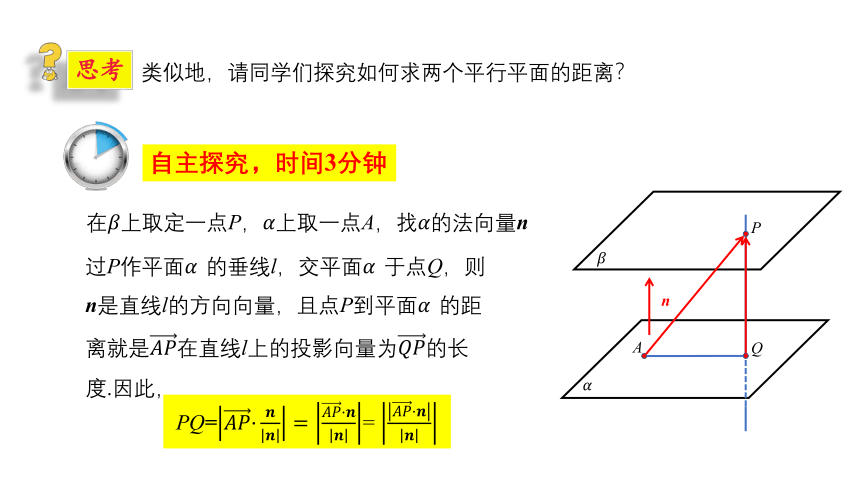
类似地,请同学们探究如何求两个平行平面的距离?
思考
自主探究,时间3分钟
n
P
A
Q
在上取定一点P,上取一点A,找的法向量n
过P作平面?的垂线l,交平面?于点Q,则n是直线l的方向向量,且点P到平面?的距离就是直线l上的投影向量为长度.因此,
PQ=
=
三.典例剖析
例6.
如图,在棱长为1的正方体ABCD-?A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、
直线的方向向量和平面的法向量,再利用有关公式,
通过坐标运算得出相应的距离.
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
(1)取=
,
=则=1,
.
=
.
所以,点B到直线的距离为
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
=
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
(2)因为//
(-1,,0)
,所以//
,所以//平面,所以点到平面的距离即为直线到平面的距离.
设平面的法向量为,则,
所以,
化简,
取z=1,则x=1,y=2,
所以,
.
又因为
(0,,0),所以点F到平面的的距离为
=
即直线FC到平面的的距离为
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
练习
1.
在棱长为1的正方体ABCD-?A1B1C1D1中,点A到平面B1C的距离等于;直线DC到平面AB1的距离等于;平面DA1到平面CB1的距离等于.
C
D
A
B
D1
A1
C1
B1
2.
在棱长为1的正方体ABCD-?A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线A
E的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离;
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
3.
如图,在棱长为1的正方体ABCD-?A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
四.课堂小结
1、点到线的距离
2、点到面的距离
PQ=
PQ=
=
l
A
u
Q
P
n
P
A
Q
五.作业布置
【课堂作业】
教材P42
T6、T7
【课时作业】
必做题:1,3,4,7,8,10
选做题:其他
人教A版(2019)选择性必修第一册
第一章
空间向量与立体几何
1.4.2
用空间向量研究距离、夹角问题
(第1课时)
一.复习回顾
前面我们研究了直线、平面的平行、垂直关系
向量平行
向量垂直
向量平行
向量垂直
向量平行
向量垂直
距离问题
角度
问题
方向向量
法向量
二.探究新知
两点间的距离
向量的模
l
A
u
Q
P
已知直线l的单位方向向量为u
,
A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
探究1
如图,直线l上的投影向量为则在直角三角形APQ
中,,∠
PAQ都是确定的.
设=a,则=(a·u)u,由勾股定理,得
PQ=
Q
l
A
P
M
l2
A
u
Q
P
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
思考
l1
自主探究,时间3分钟
设=a,则=(a·u)u,由勾股定理,得
PQ=
在l1上取定一点P,l2上取一点A
找l1或l2的方向向量u
已知平面?的法向量为n,A是平面?内的定点,P是平面?外一点.如何求点P到平面?的距离?
探究2
n
过P作平面?的垂线l,交平面?于点Q,则n是直线l的方向向量,且点P到平面?的距离就是直线l上的投影向量为长度.因此
P
A
PQ=
=
Q
类似地,请同学们探究如何求两个平行平面的距离?
思考
自主探究,时间3分钟
n
P
A
Q
在上取定一点P,上取一点A,找的法向量n
过P作平面?的垂线l,交平面?于点Q,则n是直线l的方向向量,且点P到平面?的距离就是直线l上的投影向量为长度.因此,
PQ=
=
三.典例剖析
例6.
如图,在棱长为1的正方体ABCD-?A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、
直线的方向向量和平面的法向量,再利用有关公式,
通过坐标运算得出相应的距离.
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
(1)取=
,
=则=1,
.
=
.
所以,点B到直线的距离为
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
=
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
(2)因为//
(-1,,0)
,所以//
,所以//平面,所以点到平面的距离即为直线到平面的距离.
设平面的法向量为,则,
所以,
化简,
取z=1,则x=1,y=2,
所以,
.
又因为
(0,,0),所以点F到平面的的距离为
=
即直线FC到平面的的距离为
解:以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(1,0,1),
B(1,1,1),
C(0,1,1),
C1(0,1,0),E(1,,0),
F(1,,1)所以
(0,1,0),
(-1,1,-1),
(0,,0),
(-1,,0),
,
(0,,0),
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
练习
1.
在棱长为1的正方体ABCD-?A1B1C1D1中,点A到平面B1C的距离等于;直线DC到平面AB1的距离等于;平面DA1到平面CB1的距离等于.
C
D
A
B
D1
A1
C1
B1
2.
在棱长为1的正方体ABCD-?A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线A
E的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离;
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
3.
如图,在棱长为1的正方体ABCD-?A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
C
z
D
A
B
D1
A1
C1
x
y
B1
F
E
四.课堂小结
1、点到线的距离
2、点到面的距离
PQ=
PQ=
=
l
A
u
Q
P
n
P
A
Q
五.作业布置
【课堂作业】
教材P42
T6、T7
【课时作业】
必做题:1,3,4,7,8,10
选做题:其他
