1.1.3集合的基本运算(第1课时)课件 - 2021-2022学年高一上学期数学人教B版(2019)必修第一册(共18张PPT)
文档属性
| 名称 | 1.1.3集合的基本运算(第1课时)课件 - 2021-2022学年高一上学期数学人教B版(2019)必修第一册(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
《1.1.3
集合的基本运算》
人教版高中数学B版必修第一册
第一章
第1课时(交集与并集)
情境引入
我们知道,实数有加,减,乘、除等运算,集合是否也有类似的运算呢?今天我们就来学习集合的基本运算.
问题1:观察下面的集合,集合与集合之间有什么关系?
(1)
(2)学校高一年级准备成立一个科学兴趣小组,招募成员时要求:
新课导入
新知探究
交集的概念
【想一想】
如果集合A,B没有公共元素,那么它们的交集是什么?
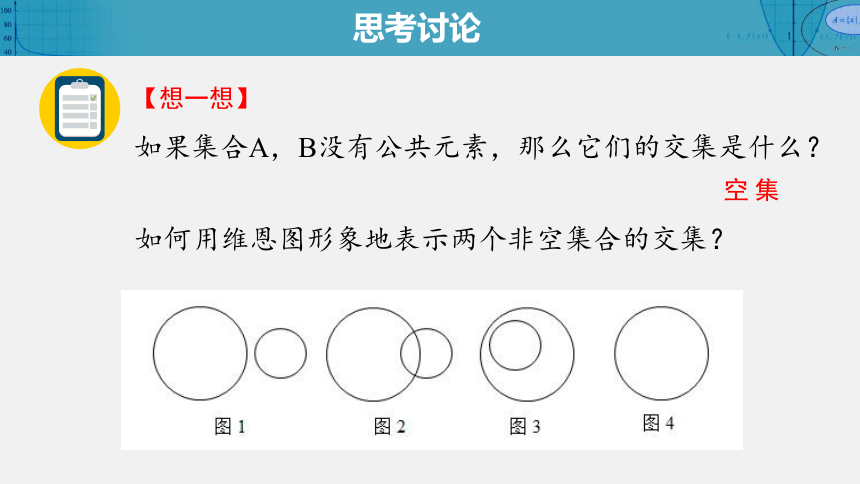
如何用维恩图形象地表示两个非空集合的交集?
空
集
思考讨论
交集运算有哪些性质?
对于任意两个集合A,B,都有:
(1)A∩B=
(2)A∩A=
(3)A∩?=?∩A=
(4)如果A?B,则A∩B=
,反之成立.
B∩A
A
?
A
问题2:
新课导入
并集的概念
新知探究
【练一练】
(1){1,3,5}∪{2,3,4,6}=_____________________.
(2)A=(-5,2),B=(-3,4],则A∪B=_________.
【尝试与发现】类比交集运算的性质,探索得出并集运算的性质,对于任意两个集合A,B,都有:
(1)A∪B=_______;
(2)A∪A=_______;
(3)A∪?=?∪A=_______;
(4)如果A?B,则A∪B=______,反之也成立.
{1,2,3,4,5,6}
(-5,4]
B∪A
A
A
B
尝试与发现
例1:求下列每对集合的交集:
(1)A={1,-3},B={-1,-3};
(2)C={1,3,5,7},D={2,4,6,8};
(3)E=(1,3],F=[-2,2).
(1){-3}
(2)
(3)(1,2)
典例讲解
例2:已知A={x|x是菱形},B={x|x是矩形},求A∩B.
A∩B={x|x是正方形}.
典例讲解
例3:已知区间A=(-3,1),B=[-2,3],
求A∩B,A∪B.
解析:在数轴上表示A和B,如图:
由图可得:
A∩B=[-2,1),A∪B=(-3,3].
典例讲解
变式训练:
设集合A={x|-3<x≤5},B={x|2<x≤6},求A∪B.
解析:画出数轴如图所示:
∴A∪B={x|-3<x≤5}∪{x|2<x≤6}={x|-3<x≤6}.
典例讲解
探索发现
(1)设有限集M所含元素的个数用card(M)表示,并规定card(φ)=0.已知A={x|x是兴趣小组的成员},B={x|x是数学兴趣小组的成员},且card(A)=20,card(B)=8,card(A∩B)=4,你能求出card(A∪B)吗?
(2)设A,B为两个有限集,讨论card(A),card(B),card(A∩B),card(A∪B)之间的关系.
当堂检测
1.
2.已知
则,
3.已知区间
,
(1)
若
,求实数
的值
(2)若
,求实数
的取值范围
归纳小结
问题:
(1)什么叫交集?交集有哪些性质?
(2)什么叫并集?并集有哪些性质?
并集运算需要注意什么?
作业:教科书第19页
练习A1,2题,练习B2题.
作业布置
教科书第20页
习题1-1A
5,6,7,8,9题;
习题1-1
B
1题.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
《1.1.3
集合的基本运算》
人教版高中数学B版必修第一册
第一章
第1课时(交集与并集)
情境引入
我们知道,实数有加,减,乘、除等运算,集合是否也有类似的运算呢?今天我们就来学习集合的基本运算.
问题1:观察下面的集合,集合与集合之间有什么关系?
(1)
(2)学校高一年级准备成立一个科学兴趣小组,招募成员时要求:
新课导入
新知探究
交集的概念
【想一想】
如果集合A,B没有公共元素,那么它们的交集是什么?
如何用维恩图形象地表示两个非空集合的交集?
空
集
思考讨论
交集运算有哪些性质?
对于任意两个集合A,B,都有:
(1)A∩B=
(2)A∩A=
(3)A∩?=?∩A=
(4)如果A?B,则A∩B=
,反之成立.
B∩A
A
?
A
问题2:
新课导入
并集的概念
新知探究
【练一练】
(1){1,3,5}∪{2,3,4,6}=_____________________.
(2)A=(-5,2),B=(-3,4],则A∪B=_________.
【尝试与发现】类比交集运算的性质,探索得出并集运算的性质,对于任意两个集合A,B,都有:
(1)A∪B=_______;
(2)A∪A=_______;
(3)A∪?=?∪A=_______;
(4)如果A?B,则A∪B=______,反之也成立.
{1,2,3,4,5,6}
(-5,4]
B∪A
A
A
B
尝试与发现
例1:求下列每对集合的交集:
(1)A={1,-3},B={-1,-3};
(2)C={1,3,5,7},D={2,4,6,8};
(3)E=(1,3],F=[-2,2).
(1){-3}
(2)
(3)(1,2)
典例讲解
例2:已知A={x|x是菱形},B={x|x是矩形},求A∩B.
A∩B={x|x是正方形}.
典例讲解
例3:已知区间A=(-3,1),B=[-2,3],
求A∩B,A∪B.
解析:在数轴上表示A和B,如图:
由图可得:
A∩B=[-2,1),A∪B=(-3,3].
典例讲解
变式训练:
设集合A={x|-3<x≤5},B={x|2<x≤6},求A∪B.
解析:画出数轴如图所示:
∴A∪B={x|-3<x≤5}∪{x|2<x≤6}={x|-3<x≤6}.
典例讲解
探索发现
(1)设有限集M所含元素的个数用card(M)表示,并规定card(φ)=0.已知A={x|x是兴趣小组的成员},B={x|x是数学兴趣小组的成员},且card(A)=20,card(B)=8,card(A∩B)=4,你能求出card(A∪B)吗?
(2)设A,B为两个有限集,讨论card(A),card(B),card(A∩B),card(A∪B)之间的关系.
当堂检测
1.
2.已知
则,
3.已知区间
,
(1)
若
,求实数
的值
(2)若
,求实数
的取值范围
归纳小结
问题:
(1)什么叫交集?交集有哪些性质?
(2)什么叫并集?并集有哪些性质?
并集运算需要注意什么?
作业:教科书第19页
练习A1,2题,练习B2题.
作业布置
教科书第20页
习题1-1A
5,6,7,8,9题;
习题1-1
B
1题.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
