冀教版数学九年级上册24.2解一元二次方程--配方法 课件 (17张PPT)
文档属性
| 名称 | 冀教版数学九年级上册24.2解一元二次方程--配方法 课件 (17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览






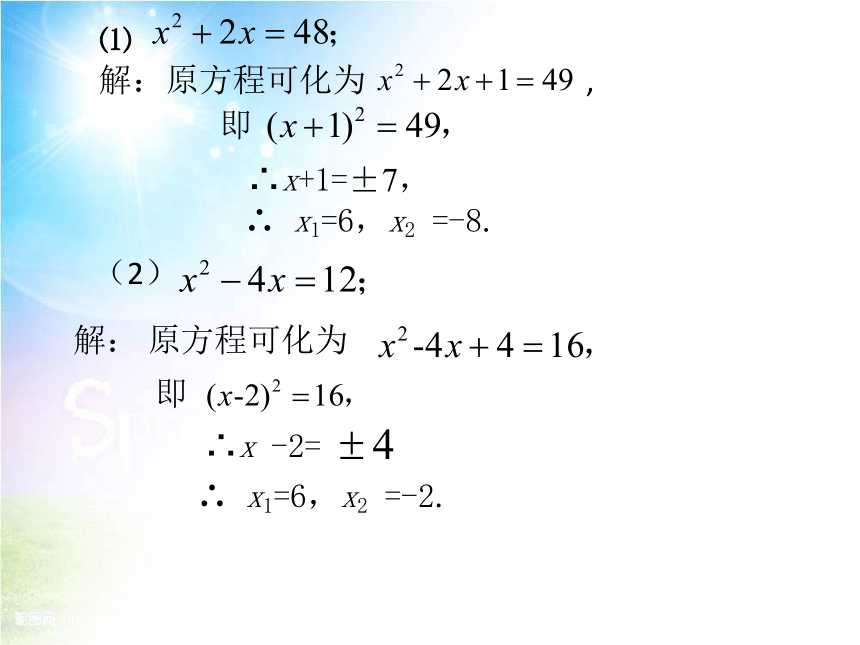
文档简介
(共17张PPT)
冀教2011课标版
九年级上册24.2
《解一元二次方程》
24.2解一元二次方程
——配方法
温故而知新
1.平方根的意义
2.完全平方公式
探究一:
1.根据平方根的意义,解下列方程:
解:(1)根据平方根的意义得
,
解:根据平方根的意义得
,
解:(1)原方程可化为
,
探究二:
解方程:
解:原方程可化为
,
即
做一做
先把下列方程化为
的形式,再求出方程的根.
⑴
(3)
(2)
(4)
根据完全平方公式填空:
(1)x2+2x+(?
)2=(x+
)2
;
(2)x2-4x+(?
)2=(x-
)2;
(3)x2-6x+(?
)2=(
)2;
(4)x2+x+(?
)2=(
)2
1
1
2
2
3
x-3
左边所填常数等于
一次项系数一半
的平方.
解:原方程可化为
,
∴x+1=±7,
∴
x1=6,x2
=-8.
解:
原方程可化为
∴x
-2=
∴
x1=6,x2
=-2.
⑴
(2)
即
即
解:
原方程可化为
即
∴x
-3=
,
∴
x1=5,x2
=1.
解:原方程可化为
即
(3)
(4)
归纳总结:
通过配方,把一元二次方程变形为一边为含未知数的一次式的平方,另一边是常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个一元一次方程,从而求出原方程的根,这种解一元二次方程的方法叫做配方法.
例1
用配方法解下列方程:
(1)
(2)
解:⑴移项,得
配方,得
即
两边开平方,得
所以
(2)
配方,得
即
两边开平方,得
所以
解:⑴移项,得
做一做
用配方法解方程:
(1)该方程能不能按上边方程
的解法先移项,然后直接配方?
观察方程移项后,二次项系数不为1,所以不能直接配方.
(2)观察该方程和上边方程有什么区别?
二次项系数不为1.
(3)如何把二次项系数化为1?
根据等式的基本性质,方程两边同时除以二次项系数可得.
(4)根据上边的分析,尝试完成解方程.
解:移项,得2x2+4x=-1,
二次项系数化为1,得x2+2x=-
,
配方,得x2+2x+1=-
+1,
即(x+1)2=
,∴x+1=±
,
∴x1=-1+
,x2=-1-
.
做一做
例2
用配方法解方程:
.
解:移项,并将二次项系数化为1,得
配方,得
,
即
两边开平方,得
所以
(5)求解(解一元一次方程).
用配方法解一元二次方程的一般步骤:
(1)移项(把常数项移到方程的右边),
(2)将二次项系数化为1(方程两边同时
除以二次项系数a);
(3)配方(方程两边都加上一次项系数的一半的平方);
(4)开平方(根据平方根意义,方程两边开平方);
练习:
解下列方程:
必做题:
课本39页习题
A组第
1,2,3
题.
选做题:
课本40页习题
B组第
1,2
题.
布置作业
冀教2011课标版
九年级上册24.2
《解一元二次方程》
24.2解一元二次方程
——配方法
温故而知新
1.平方根的意义
2.完全平方公式
探究一:
1.根据平方根的意义,解下列方程:
解:(1)根据平方根的意义得
,
解:根据平方根的意义得
,
解:(1)原方程可化为
,
探究二:
解方程:
解:原方程可化为
,
即
做一做
先把下列方程化为
的形式,再求出方程的根.
⑴
(3)
(2)
(4)
根据完全平方公式填空:
(1)x2+2x+(?
)2=(x+
)2
;
(2)x2-4x+(?
)2=(x-
)2;
(3)x2-6x+(?
)2=(
)2;
(4)x2+x+(?
)2=(
)2
1
1
2
2
3
x-3
左边所填常数等于
一次项系数一半
的平方.
解:原方程可化为
,
∴x+1=±7,
∴
x1=6,x2
=-8.
解:
原方程可化为
∴x
-2=
∴
x1=6,x2
=-2.
⑴
(2)
即
即
解:
原方程可化为
即
∴x
-3=
,
∴
x1=5,x2
=1.
解:原方程可化为
即
(3)
(4)
归纳总结:
通过配方,把一元二次方程变形为一边为含未知数的一次式的平方,另一边是常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个一元一次方程,从而求出原方程的根,这种解一元二次方程的方法叫做配方法.
例1
用配方法解下列方程:
(1)
(2)
解:⑴移项,得
配方,得
即
两边开平方,得
所以
(2)
配方,得
即
两边开平方,得
所以
解:⑴移项,得
做一做
用配方法解方程:
(1)该方程能不能按上边方程
的解法先移项,然后直接配方?
观察方程移项后,二次项系数不为1,所以不能直接配方.
(2)观察该方程和上边方程有什么区别?
二次项系数不为1.
(3)如何把二次项系数化为1?
根据等式的基本性质,方程两边同时除以二次项系数可得.
(4)根据上边的分析,尝试完成解方程.
解:移项,得2x2+4x=-1,
二次项系数化为1,得x2+2x=-
,
配方,得x2+2x+1=-
+1,
即(x+1)2=
,∴x+1=±
,
∴x1=-1+
,x2=-1-
.
做一做
例2
用配方法解方程:
.
解:移项,并将二次项系数化为1,得
配方,得
,
即
两边开平方,得
所以
(5)求解(解一元一次方程).
用配方法解一元二次方程的一般步骤:
(1)移项(把常数项移到方程的右边),
(2)将二次项系数化为1(方程两边同时
除以二次项系数a);
(3)配方(方程两边都加上一次项系数的一半的平方);
(4)开平方(根据平方根意义,方程两边开平方);
练习:
解下列方程:
必做题:
课本39页习题
A组第
1,2,3
题.
选做题:
课本40页习题
B组第
1,2
题.
布置作业
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
