冀教版数学九年级上册24.2.3解一元二次方程——因式分解法 课件 (27张ppt)
文档属性
| 名称 | 冀教版数学九年级上册24.2.3解一元二次方程——因式分解法 课件 (27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 887.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 21:17:58 | ||
图片预览








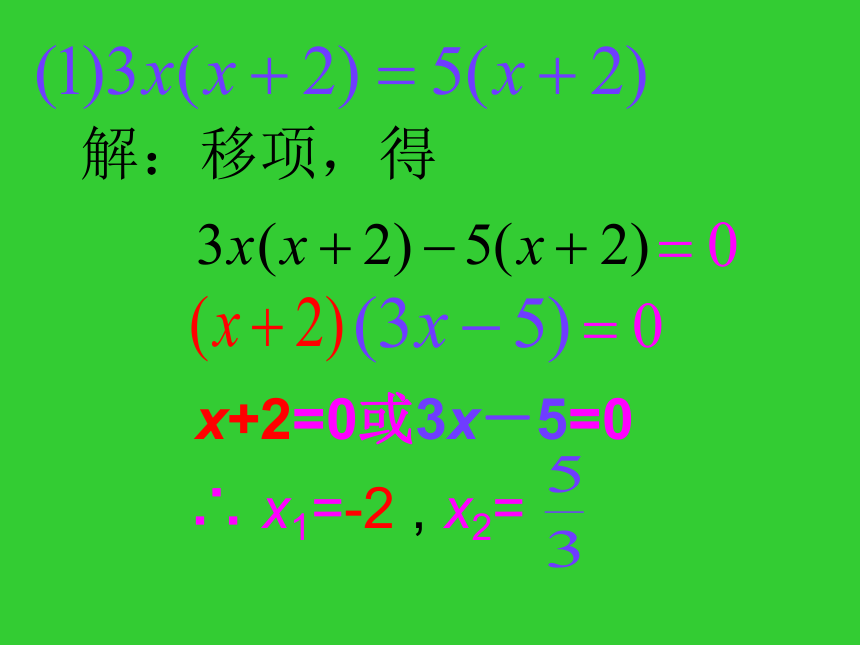
文档简介
(共27张PPT)
24.2.3用因式分解法解一元二次方程
复习引入:
1、已学过的一元二次方程解
法有哪些?
2、请用已学过的方法解方程
x2
-
4=0
x2-4=0
解:原方程可变形为
(x+2)(x-2)=0
X+2=0
或
x-2=0
∴
x1=-2
,x2=2
X2-4=
(x+2)(x-2)
AB=0?A=0或B=0
分解因式的方法有那些?
(1)提取公因式法:
(2)公式法:
(3)十字相乘法:
am+bm+cm=m(a+b+c).
a2-b2=(a+b)(a-b),
a2+2ab+b2=(a+b)2.
x2+(a+b)x+ab=
(x+a)(x+b).
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3X+5=0
或
3x-5=0
9X2-25=
(3x+5)(3x-5)
快速回答:下列各方程的根分别是多少?
AB=0?A=0或B=0
例2、解下列方程
x+2=0或3x-5=0
∴
x1=-2
,
x2=
2、(3x+1)2-5=0
解:原方程可变形为
(3x+1+
)(3x+1-
)=0
3x+1+
=0或3x+1-
=0
∴
x1=
,
x2=
这样解是否正确呢?
当一元二次方程的一边为0
,而另一边易于分解成两个一次因式时,就可以用因式分解法来解.
0
用因式分解法解一元二次方程的步骤
1o方程右边化为
。
2o将方程左边分解成两个
的乘积。
3o至少
因式为零,得到两个一元一次方程。
4o两个
就是原方程的解。
零
一次因式
有一个
一元一次方程的解
右化零 左分解
两因式 各求解
简记歌诀:
例1、解下列方程
1、x2-3x-10=0
2、(x+3)(x-1)=5
解:原方程可变形为
解:原方程可变形为
(x-5)(x+2)=0
x2+2x-8=0
(x-2)(x+4)=0
x-5=0或x+2=0
x-2=0或x+4=0
∴
x1=5
,x2=-2
∴
x1=2
,x2=-4
例
(x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴
x1=2
,x2=-4
解题步骤演示
方程右边化为零
x2+2x-8
=0
左边分解成两个一次因式
的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
下面的解法正确吗?如果不正确,错误在哪?
(
)
用因式分解法解下列方程:
y2=3y
②(2a-3)2=(a-2)(3a-4)
③
④x2+7x+12=0
①(x-5)(x+2)=18
⑤t(t+3)=28
⑥(4x-3)2=(x+3)2
解题框架图
解:原方程可变形为:
=0
(
)(
)=0
=0或
=0
∴
x1=
,
x2=
一次因式A
一次因式A
一次因式B
一次因式B
B解
A解
结束寄语
配方法和公式法是解一元二次方程重要方法,要作为一种基本技能来掌握.而某些方程可以用分解因式法简便快捷地求解.
24.2.3用因式分解法解一元二次方程
复习引入:
1、已学过的一元二次方程解
法有哪些?
2、请用已学过的方法解方程
x2
-
4=0
x2-4=0
解:原方程可变形为
(x+2)(x-2)=0
X+2=0
或
x-2=0
∴
x1=-2
,x2=2
X2-4=
(x+2)(x-2)
AB=0?A=0或B=0
分解因式的方法有那些?
(1)提取公因式法:
(2)公式法:
(3)十字相乘法:
am+bm+cm=m(a+b+c).
a2-b2=(a+b)(a-b),
a2+2ab+b2=(a+b)2.
x2+(a+b)x+ab=
(x+a)(x+b).
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3X+5=0
或
3x-5=0
9X2-25=
(3x+5)(3x-5)
快速回答:下列各方程的根分别是多少?
AB=0?A=0或B=0
例2、解下列方程
x+2=0或3x-5=0
∴
x1=-2
,
x2=
2、(3x+1)2-5=0
解:原方程可变形为
(3x+1+
)(3x+1-
)=0
3x+1+
=0或3x+1-
=0
∴
x1=
,
x2=
这样解是否正确呢?
当一元二次方程的一边为0
,而另一边易于分解成两个一次因式时,就可以用因式分解法来解.
0
用因式分解法解一元二次方程的步骤
1o方程右边化为
。
2o将方程左边分解成两个
的乘积。
3o至少
因式为零,得到两个一元一次方程。
4o两个
就是原方程的解。
零
一次因式
有一个
一元一次方程的解
右化零 左分解
两因式 各求解
简记歌诀:
例1、解下列方程
1、x2-3x-10=0
2、(x+3)(x-1)=5
解:原方程可变形为
解:原方程可变形为
(x-5)(x+2)=0
x2+2x-8=0
(x-2)(x+4)=0
x-5=0或x+2=0
x-2=0或x+4=0
∴
x1=5
,x2=-2
∴
x1=2
,x2=-4
例
(x+3)(x-1)=5
解:原方程可变形为
(x-2)(x+4)=0
x-2=0或x+4=0
∴
x1=2
,x2=-4
解题步骤演示
方程右边化为零
x2+2x-8
=0
左边分解成两个一次因式
的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
下面的解法正确吗?如果不正确,错误在哪?
(
)
用因式分解法解下列方程:
y2=3y
②(2a-3)2=(a-2)(3a-4)
③
④x2+7x+12=0
①(x-5)(x+2)=18
⑤t(t+3)=28
⑥(4x-3)2=(x+3)2
解题框架图
解:原方程可变形为:
=0
(
)(
)=0
=0或
=0
∴
x1=
,
x2=
一次因式A
一次因式A
一次因式B
一次因式B
B解
A解
结束寄语
配方法和公式法是解一元二次方程重要方法,要作为一种基本技能来掌握.而某些方程可以用分解因式法简便快捷地求解.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
