第二章 一元二次函数、方程与不等式 单元检测卷(A)——2021-2022学年高一数学上学期人教A版必修第一册(Word含答案解析)
文档属性
| 名称 | 第二章 一元二次函数、方程与不等式 单元检测卷(A)——2021-2022学年高一数学上学期人教A版必修第一册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 482.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:26:30 | ||
图片预览




文档简介
第二章
一元二次函数、方程与不等式
单元检测卷(A)
一、单选题
1.下列说法正确的是
A.某人月收入x不高于2000元可表示为“x<2000”
B.若小明的身高为x,小华的身高为y,则小明比小华矮表示为“x>y”
C.某变量x至少是a可表示为“x≥a”
D.某变量y不超过a可表示为“y≥a”
2.某同学参加期末模拟考试,考后对自己的语文和数学成绩进行了如下估计:语文成绩高于85分,数学成绩不低于80分,用不等式组可以表示为(
)
A.
B.
C.
D.
3.已知实数,记,则( )
A.
B.
C.
D.大小不确定
4.有一家三口的年龄之和为65岁,设父亲、母亲和小孩的年龄分别为、、,则下列选项中能反映、、关系的是(
)
A.
B.
C.
D.
5.已知为非零实数,且,则下列不等式成立的是(
)
A.
B.
C.
D.
6.已知,则f(x)=有
A.最大值
B.最小值
C.最大值1
D.最小值1
7.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为,三角形的面积可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三角形的边长满足,则此三角形面积的最大值为
A.
B.
C.
D.
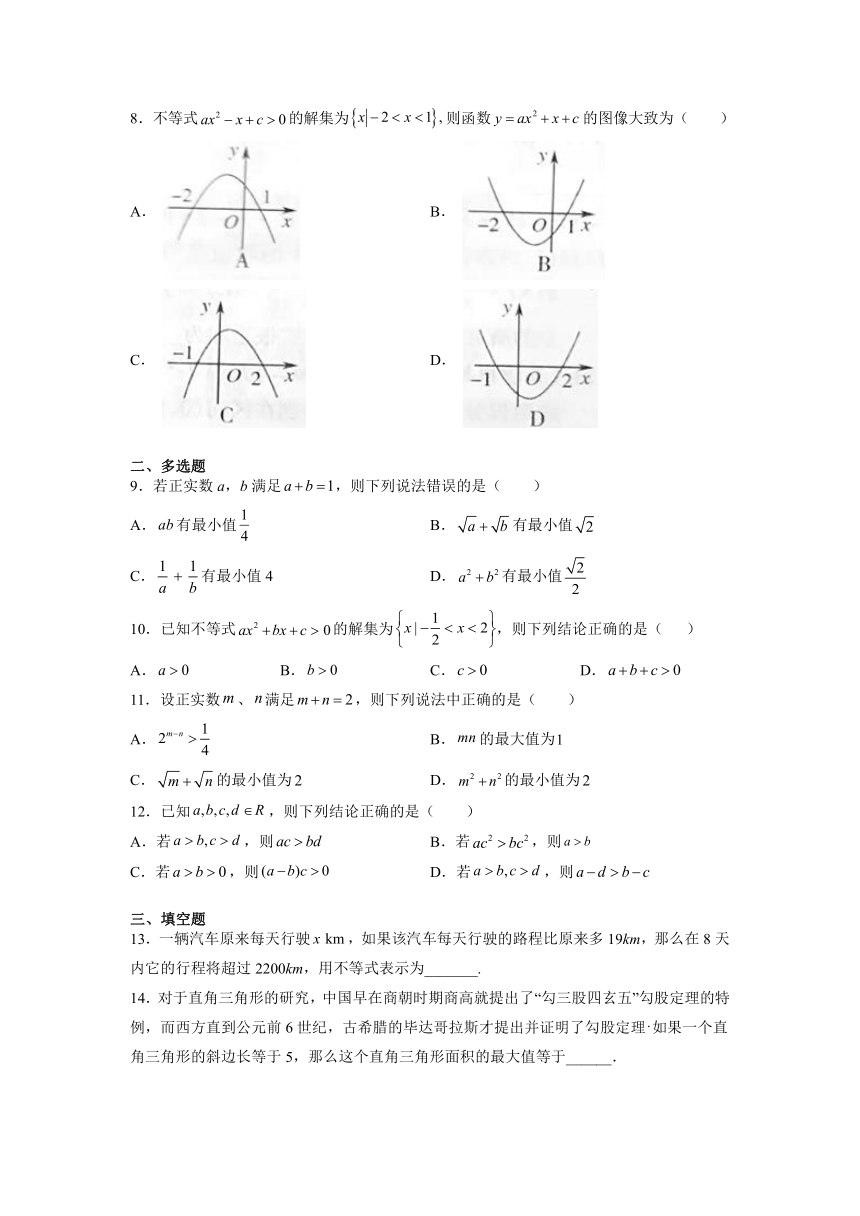
8.不等式的解集为则函数的图像大致为(
)
A.
B.
C.
D.
二、多选题
9.若正实数a,b满足,则下列说法错误的是(
)
A.有最小值
B.有最小值
C.有最小值4
D.有最小值
10.已知不等式的解集为,则下列结论正确的是(
)
A.
B.
C.
D.
11.设正实数、满足,则下列说法中正确的是(
)
A.
B.的最大值为
C.的最小值为
D.的最小值为
12.已知,则下列结论正确的是(
)
A.若,则
B.若,则
C.若,则
D.若,则
三、填空题
13.一辆汽车原来每天行驶,如果该汽车每天行驶的路程比原来多19km,那么在8天内它的行程将超过2200km,用不等式表示为_______.
14.对于直角三角形的研究,中国早在商朝时期商高就提出了“勾三股四玄五”勾股定理的特例,而西方直到公元前6世纪,古希腊的毕达哥拉斯才提出并证明了勾股定理如果一个直角三角形的斜边长等于5,那么这个直角三角形面积的最大值等于______.
15.已知,,若不等式恒成立,则的最大值为______.
16.某小型雨衣厂生产某种雨衣,售价P(元/件)与月销售量x(件)之间的关系为P=160-2x,生产x件的成本R=500+30x.若每月获得的利润y不少于1300元,则该厂的月销售量x的取值范围为______.
四、解答题
17.若不等式的解集是,
(1)求的值;
(2)求不等式的解集.
18.某家庭准备利用假期到某地旅游,有甲?乙两家旅行社提供两种优惠方案,甲旅行社的方案是:如果户主买全票一张,其余人可享受五五折优惠;乙旅行社的方案是:家庭旅游算集体票,可按七五折优惠.如果这两家旅行社的原价相同,请问该家庭选择哪家旅行社外出旅游合算?
19.设,,,求证:.
20.已知,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
21.(1)已知a,b,c∈(0,+∞).求证:.
(2)已知均为正数,且,求证:.
22.国家为了加强对烟酒生产的管理,实行征收附加税政策.现在某种酒每瓶70元,不征收附加税时,每年大约产销100万瓶;若政府征收附加税,每销售100元征收R元(叫做税率为R%),则每年产销量将减少10R万瓶.要使每年在此项经营中所收附加税不少于112万元,R应怎样确定?
参考答案
1.C
【解析】对于应满足,故中说法错误;
对于应满足,故中说法错误;
至少是可表示为“”,中说法正确;
对于与得关系可表示为,故中说法错误,故选C.
2.A
【解析】由题可知,语文成绩高于85分,数学成绩不低于80分,
.
故选:.
3.B
【解析】作差比较,,所以,
故选
B
4.C
【解析】因为一家三口的年龄之和为65岁,设父亲、母亲和小孩的年龄分别为、、,
,
又考虑到父母年龄一定大于小孩年龄且小孩年龄大于零,
故,.
故选:.
5.C
【解析】对于A,若,则,两边平方得到,故A不正确;
对于B,若,则,,则,故B不正确;
对于C,
,由于为非零数,,则,,故,即,所以C正确。
对于D,若,则,,,则,故D不正确;
故答案选C
6.D
【解析】
当即或(舍去)时,取得最小值
故选
7.C
【解析】由题意,p=10,
S8,
∴此三角形面积的最大值为8.
故选C.
8.C
9.ABD
【解析】因为正实数a,b满足,所以,,所以,故无最小值,A错误;
,故,即无最小值,故B错误;
,故有最小值4,C说法正确;
,所以有最小值,故D错误,
故选:ABD.
10.BCD
【解析】解:对A,不等式的解集为,
故相应的二次函数的图象开口向下,
即,故A错误;
对B,C,由题意知:
和是关于的方程的两个根,
则有,,
又,故,故B,C正确;
对D,,
,
又,
,故D正确.
故选:BCD.
11.ABD
【解析】对于A选项,因为正实数、满足,则,
,故,A对;
对于B选项,由基本不等式可得,当且仅当时,等号成立,B对;
对于C选项,由基本不等式可得,
因为,故,当且仅当时,等号成立,C错;
对于D选项,,
可得,当且仅当时,等号成立,D对.
故选:ABD.
12.BD
【解析】对于选项A:举反例:,,,满足,但,
故选项A
不正确;
对于选项B:因为,则,所以
,故选项B正确;
对于选项C:因为,,,满足,但,故选项C不正确;
对于选项D:因为,所以,因为,所以,故选项D正确,
故选:BD.
13.
【解析】解:由汽车原来每天行驶,又该汽车每天行驶的路程比原来多19km,即汽车每天行驶的路程为,则在8天内它的行程为,
因此,“在8天内它的行程将超过2200km”可以用不等式表示为:.
故答案为:.
14.
【解析】设直角三角形的斜边为c,直角边分别为a,b,
由题意知,
则,
则三角形的面积,
,
,
则三角形的面积,当且仅当a=b=取等
即这个直角三角形面积的最大值等于,
故答案为.
15.9.
【解析】由得恒成立,而,故,所以的最大值为.
16.
【解析】由题意,得:
,令,得,
,.
17.(1);(2).
【解析】(1)依题意可得:=0的两个实数根为和2,
由韦达定理得:,解得:;.
(2)则不等式,可化为.
所以,所以,
所以,
故不等式的解集..
18.答案见解析
【解析】解:设该家庭除户主外,还有人参加旅游,
甲?乙两旅行社收费总金额分别为,—张全票的票价为元,则只需按两家旅行社的优惠条件分别计算出,
再比较的大小即可.
∵,
而.
∴当时.
;当时,
.
又为正整数,所以当时,
,即两口之家应选择乙旅行社;
当时,
,即三口之家或多于三口的家庭应选择甲旅行社.
19.证明见解析
【解析】证明:,,,
.
当且仅当时取等号.
20.
【分析】
把用表示,可得,由,利用不等式的性质可得结论.
【解析】由题意得
解得
所以,
因为,
所以;
因为,
所以.
两式相加得,
21.(1)证明见解析;(2)证明见解析.
【解析】(1)∵,,
∴,,
即.当且仅当时,等号成立.
(2)
,即,
当且仅当时,等号成立.
22..
【解析】设产销量为每年x万瓶,则销售收入为每年70x万元,从中征收附加税为70x·R%万元,并且x=100-10R,由题意,得70(100-10R)·R%≥112,
即R2-10R+16≤0,
解得2≤R≤8,
∴税率定在2%~8%(包括2%和8%)时,可使每年在此项经营中所收附加税不少于112万元.
一元二次函数、方程与不等式
单元检测卷(A)
一、单选题
1.下列说法正确的是
A.某人月收入x不高于2000元可表示为“x<2000”
B.若小明的身高为x,小华的身高为y,则小明比小华矮表示为“x>y”
C.某变量x至少是a可表示为“x≥a”
D.某变量y不超过a可表示为“y≥a”
2.某同学参加期末模拟考试,考后对自己的语文和数学成绩进行了如下估计:语文成绩高于85分,数学成绩不低于80分,用不等式组可以表示为(
)
A.
B.
C.
D.
3.已知实数,记,则( )
A.
B.
C.
D.大小不确定
4.有一家三口的年龄之和为65岁,设父亲、母亲和小孩的年龄分别为、、,则下列选项中能反映、、关系的是(
)
A.
B.
C.
D.
5.已知为非零实数,且,则下列不等式成立的是(
)
A.
B.
C.
D.
6.已知,则f(x)=有
A.最大值
B.最小值
C.最大值1
D.最小值1
7.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为,三角形的面积可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三角形的边长满足,则此三角形面积的最大值为
A.
B.
C.
D.
8.不等式的解集为则函数的图像大致为(
)
A.
B.
C.
D.
二、多选题
9.若正实数a,b满足,则下列说法错误的是(
)
A.有最小值
B.有最小值
C.有最小值4
D.有最小值
10.已知不等式的解集为,则下列结论正确的是(
)
A.
B.
C.
D.
11.设正实数、满足,则下列说法中正确的是(
)
A.
B.的最大值为
C.的最小值为
D.的最小值为
12.已知,则下列结论正确的是(
)
A.若,则
B.若,则
C.若,则
D.若,则
三、填空题
13.一辆汽车原来每天行驶,如果该汽车每天行驶的路程比原来多19km,那么在8天内它的行程将超过2200km,用不等式表示为_______.
14.对于直角三角形的研究,中国早在商朝时期商高就提出了“勾三股四玄五”勾股定理的特例,而西方直到公元前6世纪,古希腊的毕达哥拉斯才提出并证明了勾股定理如果一个直角三角形的斜边长等于5,那么这个直角三角形面积的最大值等于______.
15.已知,,若不等式恒成立,则的最大值为______.
16.某小型雨衣厂生产某种雨衣,售价P(元/件)与月销售量x(件)之间的关系为P=160-2x,生产x件的成本R=500+30x.若每月获得的利润y不少于1300元,则该厂的月销售量x的取值范围为______.
四、解答题
17.若不等式的解集是,
(1)求的值;
(2)求不等式的解集.
18.某家庭准备利用假期到某地旅游,有甲?乙两家旅行社提供两种优惠方案,甲旅行社的方案是:如果户主买全票一张,其余人可享受五五折优惠;乙旅行社的方案是:家庭旅游算集体票,可按七五折优惠.如果这两家旅行社的原价相同,请问该家庭选择哪家旅行社外出旅游合算?
19.设,,,求证:.
20.已知,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
21.(1)已知a,b,c∈(0,+∞).求证:.
(2)已知均为正数,且,求证:.
22.国家为了加强对烟酒生产的管理,实行征收附加税政策.现在某种酒每瓶70元,不征收附加税时,每年大约产销100万瓶;若政府征收附加税,每销售100元征收R元(叫做税率为R%),则每年产销量将减少10R万瓶.要使每年在此项经营中所收附加税不少于112万元,R应怎样确定?
参考答案
1.C
【解析】对于应满足,故中说法错误;
对于应满足,故中说法错误;
至少是可表示为“”,中说法正确;
对于与得关系可表示为,故中说法错误,故选C.
2.A
【解析】由题可知,语文成绩高于85分,数学成绩不低于80分,
.
故选:.
3.B
【解析】作差比较,,所以,
故选
B
4.C
【解析】因为一家三口的年龄之和为65岁,设父亲、母亲和小孩的年龄分别为、、,
,
又考虑到父母年龄一定大于小孩年龄且小孩年龄大于零,
故,.
故选:.
5.C
【解析】对于A,若,则,两边平方得到,故A不正确;
对于B,若,则,,则,故B不正确;
对于C,
,由于为非零数,,则,,故,即,所以C正确。
对于D,若,则,,,则,故D不正确;
故答案选C
6.D
【解析】
当即或(舍去)时,取得最小值
故选
7.C
【解析】由题意,p=10,
S8,
∴此三角形面积的最大值为8.
故选C.
8.C
9.ABD
【解析】因为正实数a,b满足,所以,,所以,故无最小值,A错误;
,故,即无最小值,故B错误;
,故有最小值4,C说法正确;
,所以有最小值,故D错误,
故选:ABD.
10.BCD
【解析】解:对A,不等式的解集为,
故相应的二次函数的图象开口向下,
即,故A错误;
对B,C,由题意知:
和是关于的方程的两个根,
则有,,
又,故,故B,C正确;
对D,,
,
又,
,故D正确.
故选:BCD.
11.ABD
【解析】对于A选项,因为正实数、满足,则,
,故,A对;
对于B选项,由基本不等式可得,当且仅当时,等号成立,B对;
对于C选项,由基本不等式可得,
因为,故,当且仅当时,等号成立,C错;
对于D选项,,
可得,当且仅当时,等号成立,D对.
故选:ABD.
12.BD
【解析】对于选项A:举反例:,,,满足,但,
故选项A
不正确;
对于选项B:因为,则,所以
,故选项B正确;
对于选项C:因为,,,满足,但,故选项C不正确;
对于选项D:因为,所以,因为,所以,故选项D正确,
故选:BD.
13.
【解析】解:由汽车原来每天行驶,又该汽车每天行驶的路程比原来多19km,即汽车每天行驶的路程为,则在8天内它的行程为,
因此,“在8天内它的行程将超过2200km”可以用不等式表示为:.
故答案为:.
14.
【解析】设直角三角形的斜边为c,直角边分别为a,b,
由题意知,
则,
则三角形的面积,
,
,
则三角形的面积,当且仅当a=b=取等
即这个直角三角形面积的最大值等于,
故答案为.
15.9.
【解析】由得恒成立,而,故,所以的最大值为.
16.
【解析】由题意,得:
,令,得,
,.
17.(1);(2).
【解析】(1)依题意可得:=0的两个实数根为和2,
由韦达定理得:,解得:;.
(2)则不等式,可化为.
所以,所以,
所以,
故不等式的解集..
18.答案见解析
【解析】解:设该家庭除户主外,还有人参加旅游,
甲?乙两旅行社收费总金额分别为,—张全票的票价为元,则只需按两家旅行社的优惠条件分别计算出,
再比较的大小即可.
∵,
而.
∴当时.
;当时,
.
又为正整数,所以当时,
,即两口之家应选择乙旅行社;
当时,
,即三口之家或多于三口的家庭应选择甲旅行社.
19.证明见解析
【解析】证明:,,,
.
当且仅当时取等号.
20.
【分析】
把用表示,可得,由,利用不等式的性质可得结论.
【解析】由题意得
解得
所以,
因为,
所以;
因为,
所以.
两式相加得,
21.(1)证明见解析;(2)证明见解析.
【解析】(1)∵,,
∴,,
即.当且仅当时,等号成立.
(2)
,即,
当且仅当时,等号成立.
22..
【解析】设产销量为每年x万瓶,则销售收入为每年70x万元,从中征收附加税为70x·R%万元,并且x=100-10R,由题意,得70(100-10R)·R%≥112,
即R2-10R+16≤0,
解得2≤R≤8,
∴税率定在2%~8%(包括2%和8%)时,可使每年在此项经营中所收附加税不少于112万元.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
