12.2三角形全等的判定课后练习 2021-2022学年人教版八年级数学上册(第四课时 Word版 含答案)
文档属性
| 名称 | 12.2三角形全等的判定课后练习 2021-2022学年人教版八年级数学上册(第四课时 Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 278.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 07:46:31 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.2三角形全等的判定(第四课时)课后练习
一、选择题
1.如图,,,垂足分别为、,且,则直接判定与△APE全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
2.如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
A.0个
B.1个
C.2个
D.3个
3.如图,在中,于点,分别交,于点,,,若依据“”说明,则下列所添条件合理的是(
)
A.
B.
C.
D.
4.如图,已知在和中,,,下列条件中不能判定的是(
)
A.
B.
C.且
D.
5.如图,,,,则能证明△ABC≌△DCB的判定法是
A.
B.
C.
D.
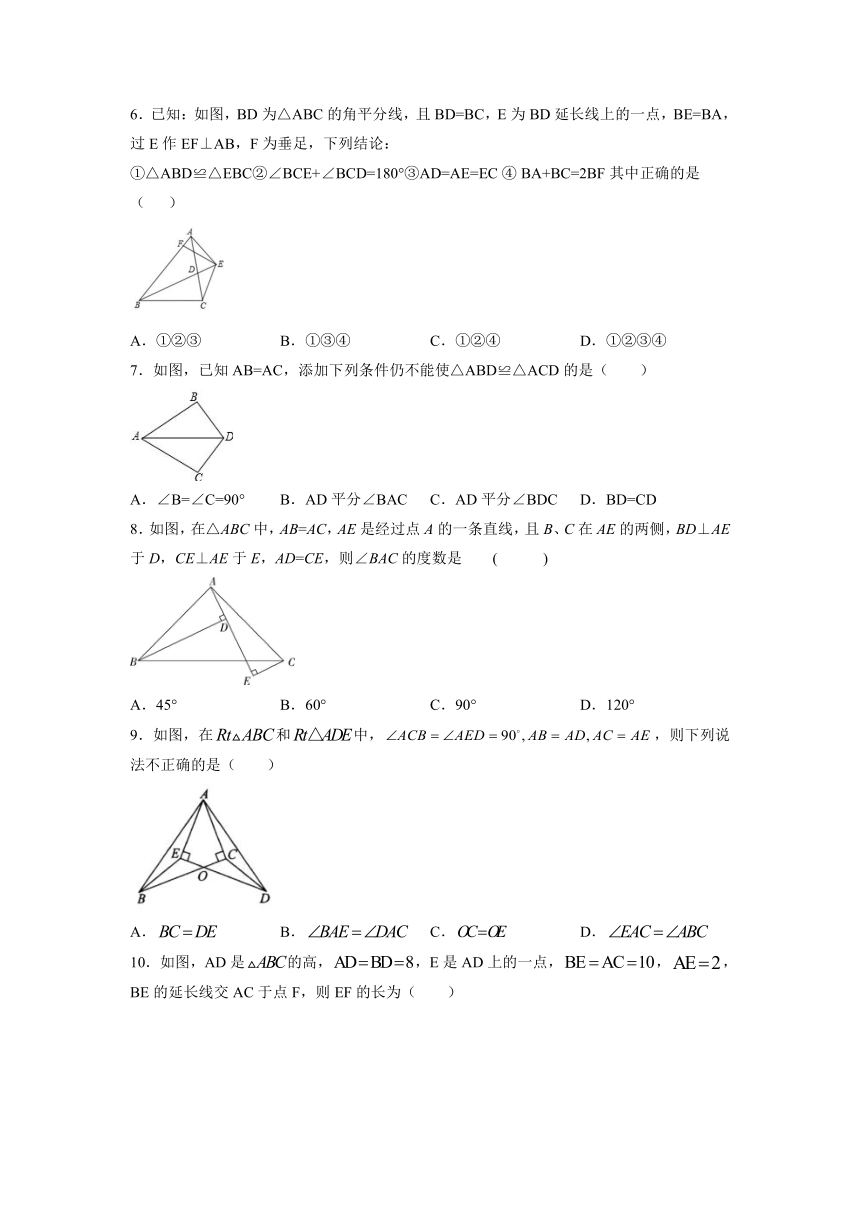
6.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC
④
BA+BC=2BF其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
7.如图,已知AB=AC,添加下列条件仍不能使△ABD≌△ACD的是(
)
A.∠B=∠C=90°
B.AD平分∠BAC
C.AD平分∠BDC
D.BD=CD
8.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是
(
)
A.45°
B.60°
C.90°
D.120°
9.如图,在和中,,则下列说法不正确的是(
)
A.
B.
C.
D.
10.如图,AD是的高,,E是AD上的一点,,,BE的延长线交AC于点F,则EF的长为(
)
A.
B.
C.
D.3
二、填空题
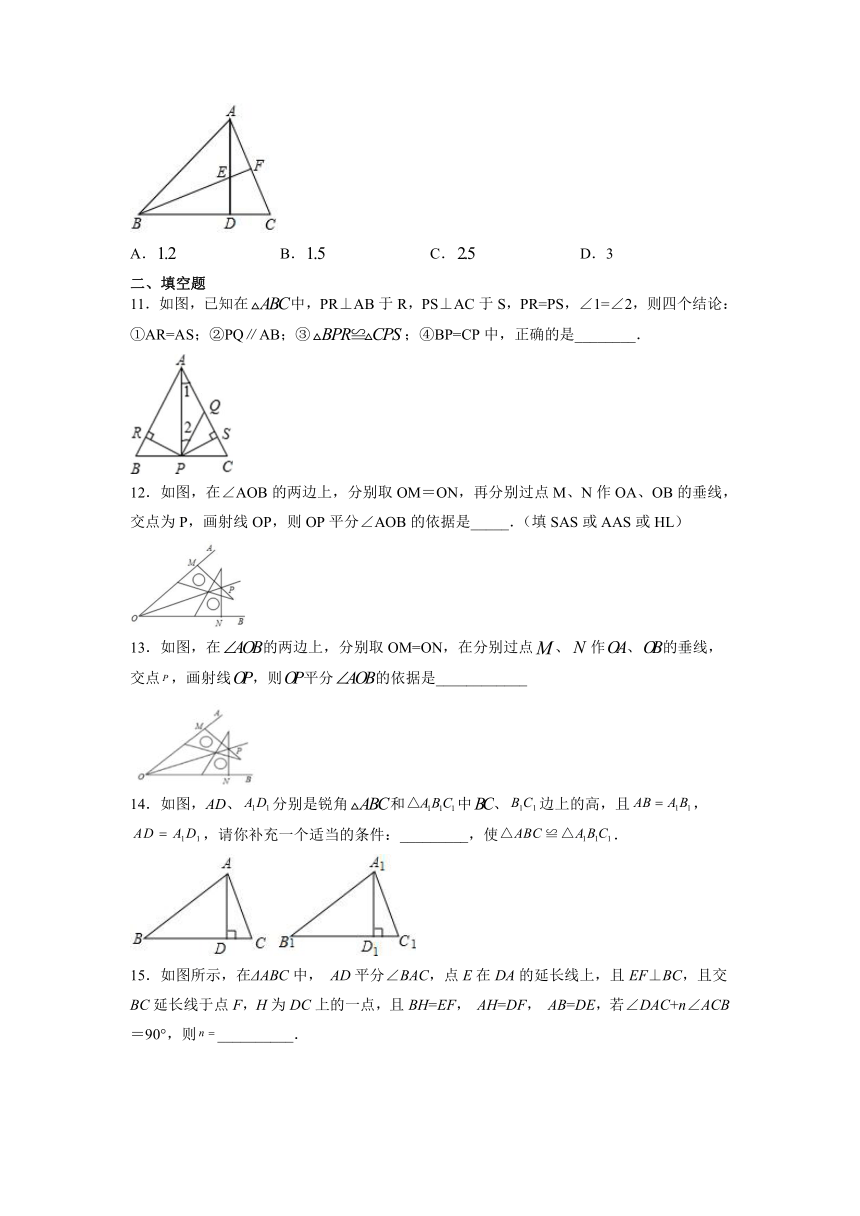
11.如图,已知在中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③;④BP=CP中,正确的是________.
12.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是_____.(填SAS或AAS或HL)
13.如图,在的两边上,分别取OM=ON,在分别过点、作、的垂线,交点,画射线,则平分的依据是____________
14.如图,AD、分别是锐角和中、边上的高,且,,请你补充一个适当的条件:_________,使.
15.如图所示,在ΔABC中,
AD平分∠BAC,点E在DA的延长线上,且EF⊥BC,且交BC延长线于点F,H为DC上的一点,且BH=EF,
AH=DF,
AB=DE,若∠DAC+n∠ACB=90°,则__________.
三、解答题
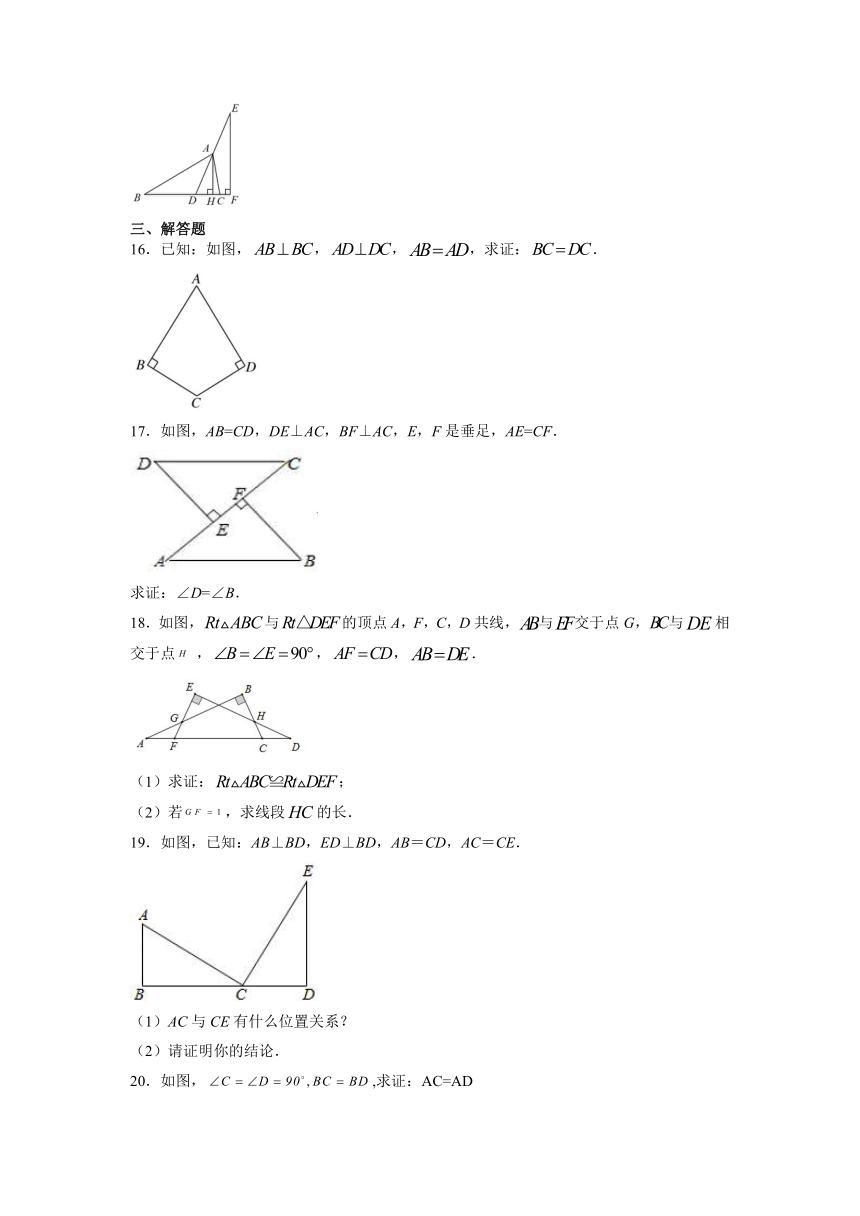
16.已知:如图,,,,求证:.
17.如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF.
求证:∠D=∠B.
18.如图,与的顶点A,F,C,D共线,与交于点G,与相交于点,,,.
(1)求证:;
(2)若,求线段的长.
19.如图,已知:AB⊥BD,ED⊥BD,AB=CD,AC=CE.
(1)AC与CE有什么位置关系?
(2)请证明你的结论.
20.如图,,求证:AC=AD
21.如图,ACBD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
22.如图所示,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC延长线于点G.求证:BF=CG.
23.如图①,平分,可得.
(1)如图②,平分,参照图①,过点D作于点交的延长线于点F,求证:;
(2)如图③,在四边形ABDC中,过点D作DE⊥AB,垂足为点E,若BE=a,则AB-AC的值是多少?(用含a的代数式表示)
【参考答案】
1.D
2.D
3.D
4.D
5.D
6.D
7.C
8.C
9.D
10.A
11.①②
12.HL
13.全等三角形判定(斜边和直角边对应相等)
14.(答案不唯一)
15.
16.证明:连接AC,如下图
∵AB⊥BC,AD⊥DC,
∴
∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC
(HL)
,
∴BC=BD
17.证明:∵AE=CF,
∴AE+EF=CF+EF,即AF=EC.
又∵BF⊥AC,DE⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF与Rt△CDE中,
,
∴Rt△ABF≌Rt△CDE(HL),
∴∠D=∠B.
18.(1)∵,
∴AF+CF=CD+CF,即AC=DF,
在与中,
∵,
∴≌(HL);
(2)∵≌,
∴∠A=∠D,∠EFD=∠BCA,
∵∠AFG=180°-∠EFD,∠DCH=180°-∠BCA,
∴∠AFG=∠DCH,
又∵,
∴?AFG≌?DCH,
∴HC=GF
=1.
19.解:(1).
(2)略
20.证明:在和中,
,
Rt△ABC≌Rt△ABD(HL)
21.证明:设AB与相交于点,
,
,
,
,
在与中,
,
,
,
,
,
,
.
22.证明:连接BE、,
,
为中点,
,
,,
且AE平分,
,
在和中,
,
,
.
23.解:(1)作DE⊥AB于E,DF⊥AC于F,如图2所示,
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠ABD=∠FCD,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DB=DC;
(2)连接AD,作DF⊥AC于F,如图3所示,
∵∠ACD=135°,
∴∠FCD=180°-∠ACD=45°,
∴∠B=45°,
∴∠FCD=∠B,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AF=AE,
∴AB=AE+BE=AC+CF+BE=AC+2BE,
∴AB-AC=2BE=2a.
第十二章全等三角形
12.2三角形全等的判定(第四课时)课后练习
一、选择题
1.如图,,,垂足分别为、,且,则直接判定与△APE全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
2.如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
A.0个
B.1个
C.2个
D.3个
3.如图,在中,于点,分别交,于点,,,若依据“”说明,则下列所添条件合理的是(
)
A.
B.
C.
D.
4.如图,已知在和中,,,下列条件中不能判定的是(
)
A.
B.
C.且
D.
5.如图,,,,则能证明△ABC≌△DCB的判定法是
A.
B.
C.
D.
6.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC
④
BA+BC=2BF其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
7.如图,已知AB=AC,添加下列条件仍不能使△ABD≌△ACD的是(
)
A.∠B=∠C=90°
B.AD平分∠BAC
C.AD平分∠BDC
D.BD=CD
8.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是
(
)
A.45°
B.60°
C.90°
D.120°
9.如图,在和中,,则下列说法不正确的是(
)
A.
B.
C.
D.
10.如图,AD是的高,,E是AD上的一点,,,BE的延长线交AC于点F,则EF的长为(
)
A.
B.
C.
D.3
二、填空题
11.如图,已知在中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③;④BP=CP中,正确的是________.
12.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是_____.(填SAS或AAS或HL)
13.如图,在的两边上,分别取OM=ON,在分别过点、作、的垂线,交点,画射线,则平分的依据是____________
14.如图,AD、分别是锐角和中、边上的高,且,,请你补充一个适当的条件:_________,使.
15.如图所示,在ΔABC中,
AD平分∠BAC,点E在DA的延长线上,且EF⊥BC,且交BC延长线于点F,H为DC上的一点,且BH=EF,
AH=DF,
AB=DE,若∠DAC+n∠ACB=90°,则__________.
三、解答题
16.已知:如图,,,,求证:.
17.如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,AE=CF.
求证:∠D=∠B.
18.如图,与的顶点A,F,C,D共线,与交于点G,与相交于点,,,.
(1)求证:;
(2)若,求线段的长.
19.如图,已知:AB⊥BD,ED⊥BD,AB=CD,AC=CE.
(1)AC与CE有什么位置关系?
(2)请证明你的结论.
20.如图,,求证:AC=AD
21.如图,ACBD,∠C=90°,AC=BE,AB=DE,求证:DE⊥AB.
22.如图所示,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC延长线于点G.求证:BF=CG.
23.如图①,平分,可得.
(1)如图②,平分,参照图①,过点D作于点交的延长线于点F,求证:;
(2)如图③,在四边形ABDC中,过点D作DE⊥AB,垂足为点E,若BE=a,则AB-AC的值是多少?(用含a的代数式表示)
【参考答案】
1.D
2.D
3.D
4.D
5.D
6.D
7.C
8.C
9.D
10.A
11.①②
12.HL
13.全等三角形判定(斜边和直角边对应相等)
14.(答案不唯一)
15.
16.证明:连接AC,如下图
∵AB⊥BC,AD⊥DC,
∴
∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC
(HL)
,
∴BC=BD
17.证明:∵AE=CF,
∴AE+EF=CF+EF,即AF=EC.
又∵BF⊥AC,DE⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF与Rt△CDE中,
,
∴Rt△ABF≌Rt△CDE(HL),
∴∠D=∠B.
18.(1)∵,
∴AF+CF=CD+CF,即AC=DF,
在与中,
∵,
∴≌(HL);
(2)∵≌,
∴∠A=∠D,∠EFD=∠BCA,
∵∠AFG=180°-∠EFD,∠DCH=180°-∠BCA,
∴∠AFG=∠DCH,
又∵,
∴?AFG≌?DCH,
∴HC=GF
=1.
19.解:(1).
(2)略
20.证明:在和中,
,
Rt△ABC≌Rt△ABD(HL)
21.证明:设AB与相交于点,
,
,
,
,
在与中,
,
,
,
,
,
,
.
22.证明:连接BE、,
,
为中点,
,
,,
且AE平分,
,
在和中,
,
,
.
23.解:(1)作DE⊥AB于E,DF⊥AC于F,如图2所示,
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠ABD=∠FCD,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DB=DC;
(2)连接AD,作DF⊥AC于F,如图3所示,
∵∠ACD=135°,
∴∠FCD=180°-∠ACD=45°,
∴∠B=45°,
∴∠FCD=∠B,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AF=AE,
∴AB=AE+BE=AC+CF+BE=AC+2BE,
∴AB-AC=2BE=2a.
