2.3用公式法求解一元二次方程 课后培优 2021-2022学年九年级数学北师大版上册(Word版 含答案)
文档属性
| 名称 | 2.3用公式法求解一元二次方程 课后培优 2021-2022学年九年级数学北师大版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 300.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 07:54:09 | ||
图片预览



文档简介
用公式法求解一元二次方程
一、单选题
1.已知方程有两个实数根,则k的取值范围是(
)
A.
B.
C.且
D.且
2.一元二次方程的根的情况是(
)
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根
3.解方程时,下面说法正确的是(
)
A.只能用公式法
B.不能用配方法
C.只能用配方法
D.公式法、配方法都能用
4.下列关于的方程中一定没有实数根的是(
)
A.
B.
C.
D.
5.如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个实数根,那么k的取值范围是(
)
A.k>﹣
B.k>﹣且k≠0
C.﹣且k≠0
D.k且k≠0
6.关于的一元二次方程的两个实数根分别是,,且以,,6为三边的三角形恰好是等腰三角形,则的值为( )
A.24
B.25
C.24或25
D.无法确定
7.已知a是一元二次方程2x2﹣2x﹣1=0较大的实数根,那么a的值应在( )
A.3和4之间
B.2和3之间
C.1和2之间
D.0和1之间
8.用公式法解方程所得的解正确的是(
)
A.
B.
C.
D.
9.是下列哪个一元二次方程的根(
)
A.
B.
C.
D.
10.用公式法解方程时,,,的值为(
)
A.
B.
C.
D.
11.用求根公式法解得某方程的两个根互为相反数,则(
)
A.
B.
C.
D.
12.一元二次方程的解为(
)
A.
B.
C.
D.无实数解
二、填空题
13.一般地,式子叫做一元二次方程的根的_____________,通常用希腊字母“_________”表示它,即.
14.用公式法解一元二次方程,得y=,请你写出该方程___.
15.一元二次方程的解为________.
16.等腰三角形的一边长为4,另两边的长是关于的方程的两个实数根,则该等腰三角形的周长是______.
17.对于实数m,n,定义运算m?n=mn2﹣n.若2?a=1?(﹣2)则a=___________.
三、解答题
18.用公式法解下列方程:
(1)
(2)
(3)
(4)
19.关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于3,求的取值范围.
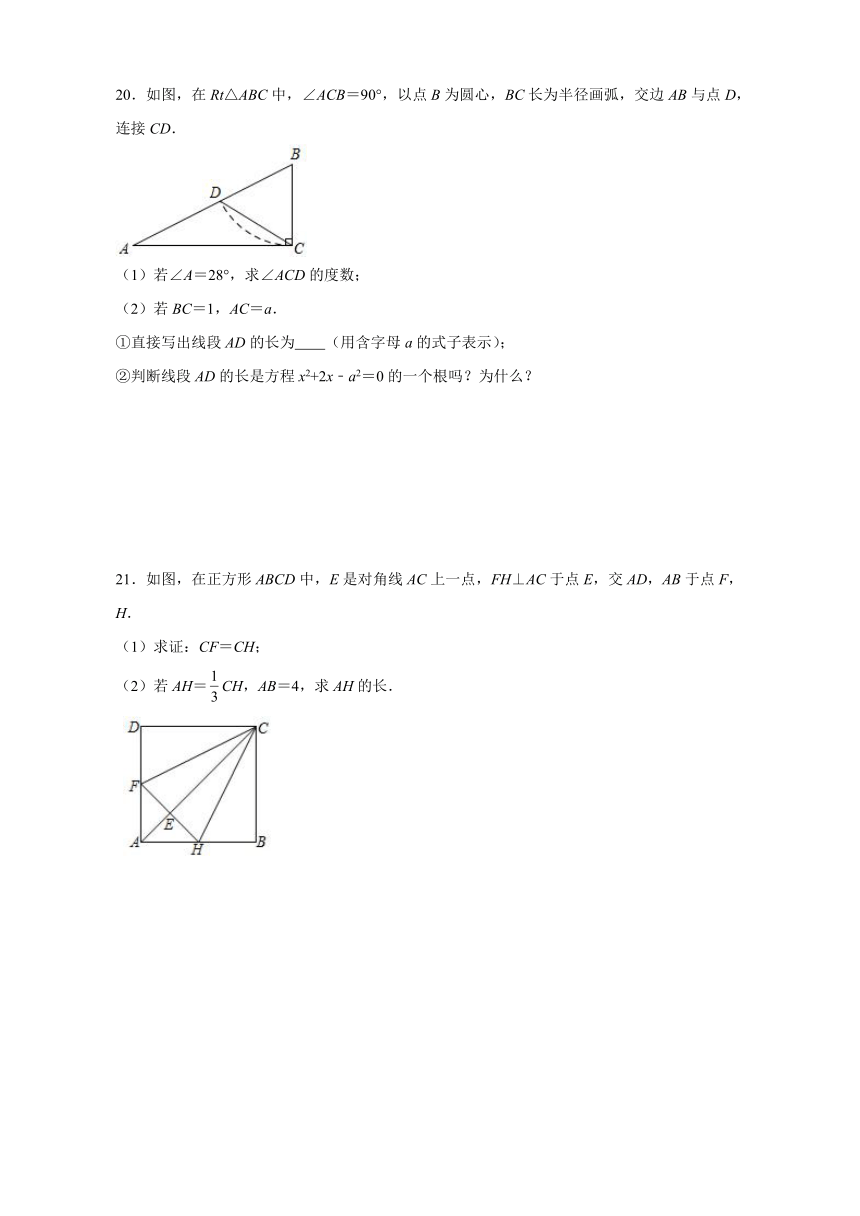
20.如图,在Rt△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)若BC=1,AC=a.
①直接写出线段AD的长为 (用含字母a的式子表示);
②判断线段AD的长是方程x2+2x﹣a2=0的一个根吗?为什么?
21.如图,在正方形ABCD中,E是对角线AC上一点,FH⊥AC于点E,交AD,AB于点F,H.
(1)求证:CF=CH;
(2)若AH=CH,AB=4,求AH的长.
参考答案
1.D
解:∵方程有两个实数根,
∴且,
解得且,
故选D.
2.C
解:∵,
∴一元二次方程有两个相等的实数根.
故选C.
3.D
解:∵有实根,
任何有实根的一元二次方程都可用配方法和公式法求解.
故选:D
4.A
解:A、,无实数根;则A符合题意;
B、,有两个不相等的实数根;则B不符合题意;
C、,有两个不相等的实数根;则C不符合题意;
D、,有两个不相等的实数根;则D不符合题意;
故选:A
5.C
解:由题意知,k2≠0,且△=b2-4ac=(2k+1)2-4k2=4k+1≥0.
解得k≥-且k≠0.
故选:C.
6.C
解:①当6为底边时,则,
∴,
∴,
∴方程为,
解得:,
∵,
∴5,5,6能构成等腰三角形;
②当6为腰时,则设,
∴,
∴,
∴方程为,
∴,,
∵,
∴4,6,6能构成等腰三角形;
综上所述:或25.
故选:C.
7.C
解:解方程2x2﹣2x﹣1=0得
,
∵a是方程2x2﹣2x﹣1=0较大的根,
∴a=,
∵1<<2,
∴2<<3,
即1<a<.
故选:C
8.D
解:,
这里a=1,b=-6,c=1,
∵△=36-4=32>0,
∴x==
,
故选:D.
9.C
解:A、的解为,不符合题意;
B、的解为,不符合题意;
C、的解为,符合题意;
D、的解为,不符合题意;
故选:C.
10.D
解:∵
∴
∴,,.
故选:D
11.A
解:方程有两根,
且.
求根公式得到方程的根为,两根互为相反数,
所以,即,
解得.
故选:A.
12.C
解:把x-2看作一个整体,a=2,b=7,c=6,
则根据一元二次方程的求根公式,得:,
∴或,
解得:,.
故选:C.
13.判别式
解:略
14.
解:设该方程为,
由得:,
则该方程为,
故答案为:.
15.
,
解:∵a=
,b=-1,c=-3,
∴△=b2-4ac=(-1)2-4×
×(-3)=7>0,
∴,
故答案为:,.
16.16
解:分为两种情况:
情况一:当腰为4时,则另一腰4是方程的一个解,
代入4到方程中,求得,
此时方程的两个解为4和8,
对应的三边长为4、4、8,不能构成三角形,故舍去;
情况二:当底边为4时,此时方程有两个相等的实数根,
∴△=12?-4k=0,解得k=36,
此时方程的两个解为6和6,
对应的三边长为6、6、4,能构成三角形,此时三角形周长为16,
故答案为:16.
17.2或.
解:根据定义,2?a=1?(﹣2)转化为:2a2﹣a=1×(﹣2)2﹣(﹣2),
解方程得,a1=2,a1=,
故答案为:2或.
18.(1);(2)(3);(4)无解
解:(1)∵,
∴,
∴,
∴原方程的根为:;
(2)原方程化为一般形式为:,
∵,
∴,
∴,
∴原方程的根为:.
(3)原方程化为
,
,
由求根公式得,,
所以原方程的解为
;
(4)
,
原方程无实数根.
19.(1)见解析;(2)m的取值范围是m>1
解:(1)证明:∵,,,
依题意,得Δ=[-(m+3)]2-4(m+2)=(m+1)2,
∵(m+1)2≥0,
∴方程总有两个实数根;
(2)由求根公式,得,
∴x1=1,x2=m+2,
∵方程有一个根大于3,
∴m+2>3.
∴m>1.
∴m的取值范围是m>1.
20.(1)∠ACD=31°;(2)①﹣1;②线段AD的长是方程x2+2x﹣a2=0的一个根.理由见解析.
解:(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°﹣∠BCD=31°;
(2)①﹣1;
理由如下:AB==,BD=BC,
∴AD=﹣1,
故答案为:﹣1;
②解方程x2+2x﹣a2=0得,
x==﹣1,
∴线段AD的长是方程x2+2x﹣a2=0的一个根.
21.(1)见解析;(2)
解:(1)∵四边形ABCD是正方形
∴∠FAE=∠HAE=45°
∵FH⊥AC
∴∠AEF=∠AEH=90°
在△FEA和△HEA中
∴△FEA≌△HEA(ASA)
∴EF=EH
∴AC垂直平分线段FH
∴CF=CH
(2)∵四边形ABCD是正方形
∴BC=AB=4,∠B=90°
设AH=x,则BH=AB-AH=4-x
∵AH=CH
∴CH=3x
在Rt△CBH中,由勾股定理得:
即
化简得:
解得:,(舍去)
∴
即AH的长为
一、单选题
1.已知方程有两个实数根,则k的取值范围是(
)
A.
B.
C.且
D.且
2.一元二次方程的根的情况是(
)
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根
3.解方程时,下面说法正确的是(
)
A.只能用公式法
B.不能用配方法
C.只能用配方法
D.公式法、配方法都能用
4.下列关于的方程中一定没有实数根的是(
)
A.
B.
C.
D.
5.如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个实数根,那么k的取值范围是(
)
A.k>﹣
B.k>﹣且k≠0
C.﹣且k≠0
D.k且k≠0
6.关于的一元二次方程的两个实数根分别是,,且以,,6为三边的三角形恰好是等腰三角形,则的值为( )
A.24
B.25
C.24或25
D.无法确定
7.已知a是一元二次方程2x2﹣2x﹣1=0较大的实数根,那么a的值应在( )
A.3和4之间
B.2和3之间
C.1和2之间
D.0和1之间
8.用公式法解方程所得的解正确的是(
)
A.
B.
C.
D.
9.是下列哪个一元二次方程的根(
)
A.
B.
C.
D.
10.用公式法解方程时,,,的值为(
)
A.
B.
C.
D.
11.用求根公式法解得某方程的两个根互为相反数,则(
)
A.
B.
C.
D.
12.一元二次方程的解为(
)
A.
B.
C.
D.无实数解
二、填空题
13.一般地,式子叫做一元二次方程的根的_____________,通常用希腊字母“_________”表示它,即.
14.用公式法解一元二次方程,得y=,请你写出该方程___.
15.一元二次方程的解为________.
16.等腰三角形的一边长为4,另两边的长是关于的方程的两个实数根,则该等腰三角形的周长是______.
17.对于实数m,n,定义运算m?n=mn2﹣n.若2?a=1?(﹣2)则a=___________.
三、解答题
18.用公式法解下列方程:
(1)
(2)
(3)
(4)
19.关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于3,求的取值范围.
20.如图,在Rt△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)若BC=1,AC=a.
①直接写出线段AD的长为 (用含字母a的式子表示);
②判断线段AD的长是方程x2+2x﹣a2=0的一个根吗?为什么?
21.如图,在正方形ABCD中,E是对角线AC上一点,FH⊥AC于点E,交AD,AB于点F,H.
(1)求证:CF=CH;
(2)若AH=CH,AB=4,求AH的长.
参考答案
1.D
解:∵方程有两个实数根,
∴且,
解得且,
故选D.
2.C
解:∵,
∴一元二次方程有两个相等的实数根.
故选C.
3.D
解:∵有实根,
任何有实根的一元二次方程都可用配方法和公式法求解.
故选:D
4.A
解:A、,无实数根;则A符合题意;
B、,有两个不相等的实数根;则B不符合题意;
C、,有两个不相等的实数根;则C不符合题意;
D、,有两个不相等的实数根;则D不符合题意;
故选:A
5.C
解:由题意知,k2≠0,且△=b2-4ac=(2k+1)2-4k2=4k+1≥0.
解得k≥-且k≠0.
故选:C.
6.C
解:①当6为底边时,则,
∴,
∴,
∴方程为,
解得:,
∵,
∴5,5,6能构成等腰三角形;
②当6为腰时,则设,
∴,
∴,
∴方程为,
∴,,
∵,
∴4,6,6能构成等腰三角形;
综上所述:或25.
故选:C.
7.C
解:解方程2x2﹣2x﹣1=0得
,
∵a是方程2x2﹣2x﹣1=0较大的根,
∴a=,
∵1<<2,
∴2<<3,
即1<a<.
故选:C
8.D
解:,
这里a=1,b=-6,c=1,
∵△=36-4=32>0,
∴x==
,
故选:D.
9.C
解:A、的解为,不符合题意;
B、的解为,不符合题意;
C、的解为,符合题意;
D、的解为,不符合题意;
故选:C.
10.D
解:∵
∴
∴,,.
故选:D
11.A
解:方程有两根,
且.
求根公式得到方程的根为,两根互为相反数,
所以,即,
解得.
故选:A.
12.C
解:把x-2看作一个整体,a=2,b=7,c=6,
则根据一元二次方程的求根公式,得:,
∴或,
解得:,.
故选:C.
13.判别式
解:略
14.
解:设该方程为,
由得:,
则该方程为,
故答案为:.
15.
,
解:∵a=
,b=-1,c=-3,
∴△=b2-4ac=(-1)2-4×
×(-3)=7>0,
∴,
故答案为:,.
16.16
解:分为两种情况:
情况一:当腰为4时,则另一腰4是方程的一个解,
代入4到方程中,求得,
此时方程的两个解为4和8,
对应的三边长为4、4、8,不能构成三角形,故舍去;
情况二:当底边为4时,此时方程有两个相等的实数根,
∴△=12?-4k=0,解得k=36,
此时方程的两个解为6和6,
对应的三边长为6、6、4,能构成三角形,此时三角形周长为16,
故答案为:16.
17.2或.
解:根据定义,2?a=1?(﹣2)转化为:2a2﹣a=1×(﹣2)2﹣(﹣2),
解方程得,a1=2,a1=,
故答案为:2或.
18.(1);(2)(3);(4)无解
解:(1)∵,
∴,
∴,
∴原方程的根为:;
(2)原方程化为一般形式为:,
∵,
∴,
∴,
∴原方程的根为:.
(3)原方程化为
,
,
由求根公式得,,
所以原方程的解为
;
(4)
,
原方程无实数根.
19.(1)见解析;(2)m的取值范围是m>1
解:(1)证明:∵,,,
依题意,得Δ=[-(m+3)]2-4(m+2)=(m+1)2,
∵(m+1)2≥0,
∴方程总有两个实数根;
(2)由求根公式,得,
∴x1=1,x2=m+2,
∵方程有一个根大于3,
∴m+2>3.
∴m>1.
∴m的取值范围是m>1.
20.(1)∠ACD=31°;(2)①﹣1;②线段AD的长是方程x2+2x﹣a2=0的一个根.理由见解析.
解:(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°﹣∠BCD=31°;
(2)①﹣1;
理由如下:AB==,BD=BC,
∴AD=﹣1,
故答案为:﹣1;
②解方程x2+2x﹣a2=0得,
x==﹣1,
∴线段AD的长是方程x2+2x﹣a2=0的一个根.
21.(1)见解析;(2)
解:(1)∵四边形ABCD是正方形
∴∠FAE=∠HAE=45°
∵FH⊥AC
∴∠AEF=∠AEH=90°
在△FEA和△HEA中
∴△FEA≌△HEA(ASA)
∴EF=EH
∴AC垂直平分线段FH
∴CF=CH
(2)∵四边形ABCD是正方形
∴BC=AB=4,∠B=90°
设AH=x,则BH=AB-AH=4-x
∵AH=CH
∴CH=3x
在Rt△CBH中,由勾股定理得:
即
化简得:
解得:,(舍去)
∴
即AH的长为
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
