2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步能力达标测评(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.3正方形的性质与判定同步能力达标测评(Word版,含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 418.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册《1.3正方形的性质与判定》
同步能力达标测评(附答案)
一.选择题(共8小题,每小题4分,共计32分)
1.如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,已知AD=6(正方形的四条边都相等,四个内角都是直角),DF=2,则S△AEF=( )
A.6
B.12
C.15
D.30
2.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是2,则BD的长为( )
A.
B.2
C.2
D.4
3.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作DF⊥DE交BC的延长线于点F,连结EF.若AE=2,则EF的值为( )
A.6
B.
C.
D.5
4.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是( )
A.BE=AE
B.PC=PD
C.∠EAF+∠AFD=90°
D.PE=EC
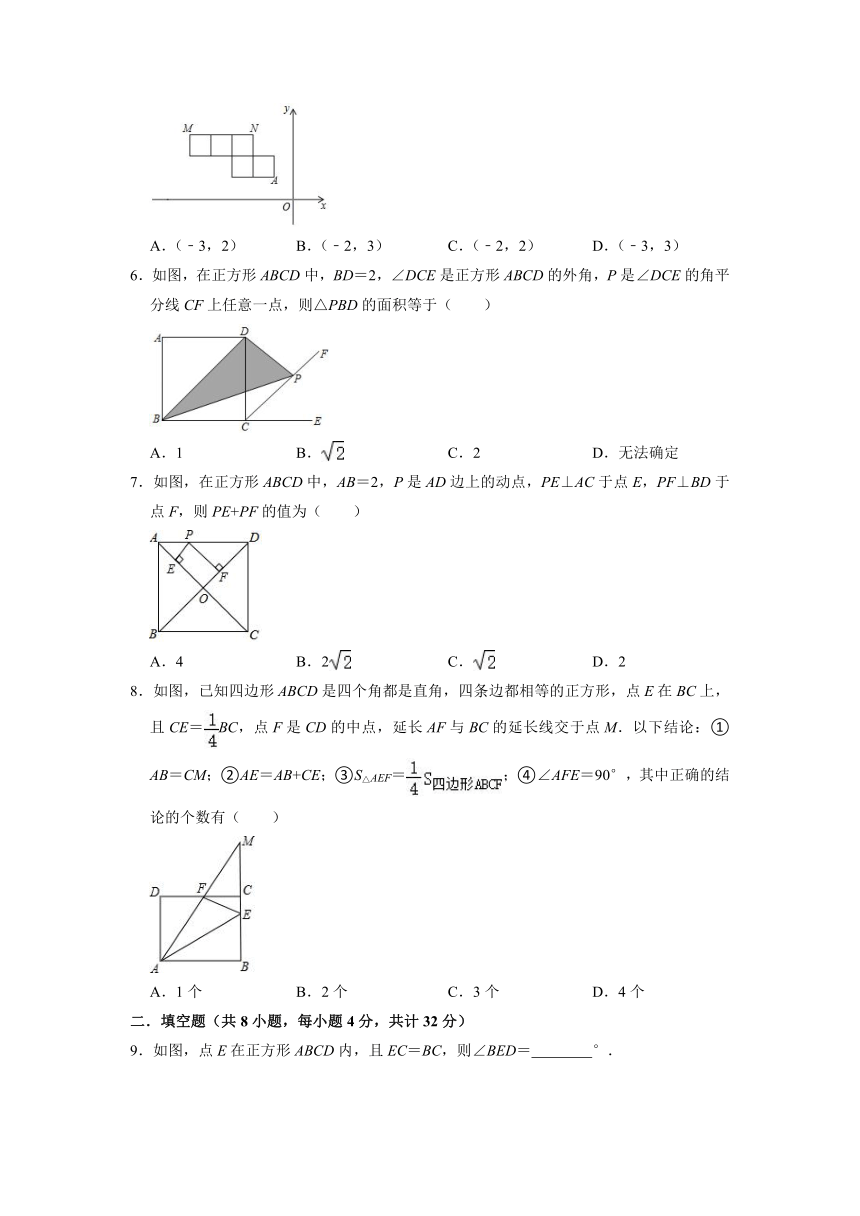
5.如图,将5个大小相同的正方形置于平面直角坐标系中,如果顶点M、N的坐标分别为(﹣14,9)、(﹣5,9),则顶点A的坐标为( )
A.(﹣3,2)
B.(﹣2,3)
C.(﹣2,2)
D.(﹣3,3)
6.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.1
B.
C.2
D.无法确定
7.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4
B.2
C.
D.2
8.如图,已知四边形ABCD是四个角都是直角,四条边都相等的正方形,点E在BC上,且CE=BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=;④∠AFE=90°,其中正确的结论的个数有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,每小题4分,共计32分)
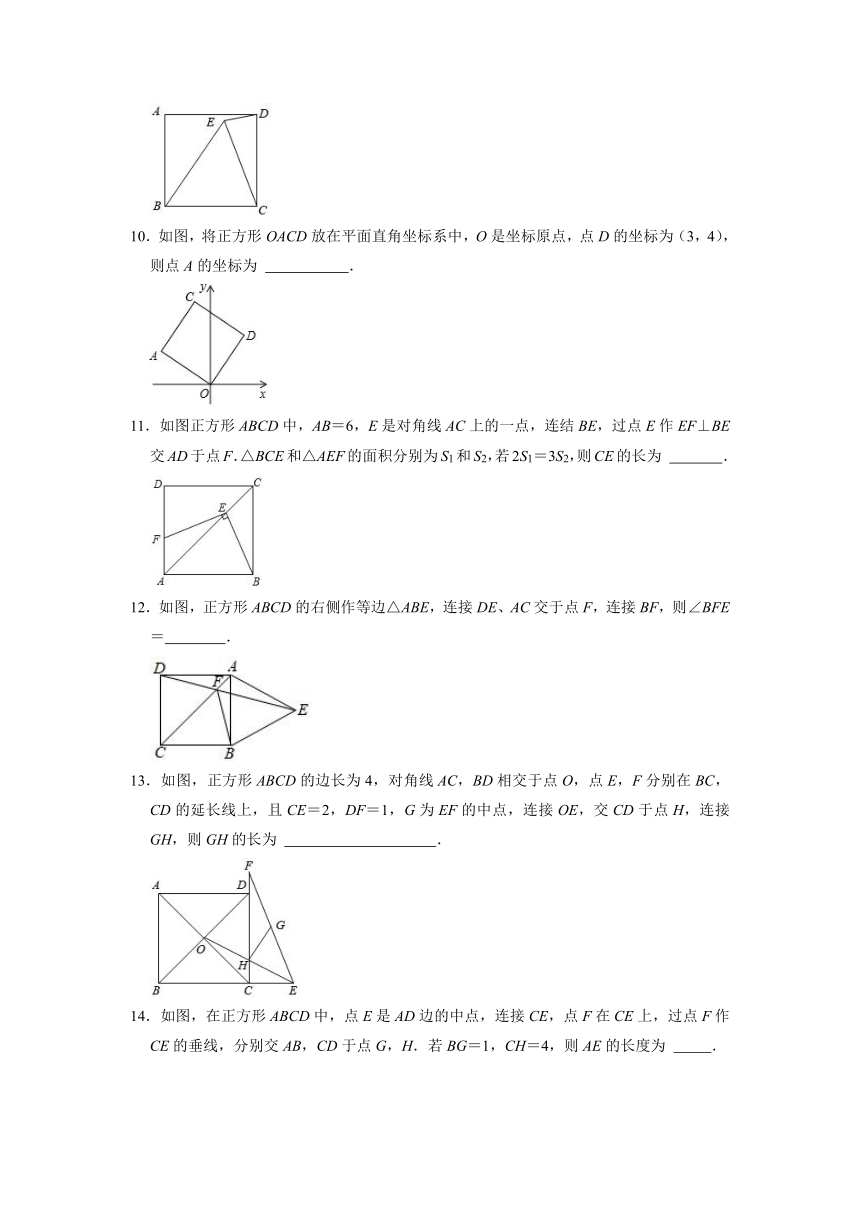
9.如图,点E在正方形ABCD内,且EC=BC,则∠BED=
°.
10.如图,将正方形OACD放在平面直角坐标系中,O是坐标原点,点D的坐标为(3,4),则点A的坐标为
.
11.如图正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为
.
12.如图,正方形ABCD的右侧作等边△ABE,连接DE、AC交于点F,连接BF,则∠BFE=
.
13.如图,正方形ABCD的边长为4,对角线AC,BD相交于点O,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H,连接GH,则GH的长为
.
14.如图,在正方形ABCD中,点E是AD边的中点,连接CE,点F在CE上,过点F作CE的垂线,分别交AB,CD于点G,H.若BG=1,CH=4,则AE的长度为
.
15.如图,在边长为4的正方形ABCD中,E、F分别是边BC、DC上的动点,且EF=4,Q为EF中点,P是边AD上的一个动点,则PQ+PB的最小值是
.
16.如图,正方形ABCD的边长为4,E为CD中点,F为BC边上一点,且CF=1,连AF,EG⊥AF交BC于G,则BG=
.
三.解答题(共7小题,每小题8分,共计56分)
17.如图,正方形ABCD中,点O为对角线AC的中点,点P为平面内外一点,且BP⊥CP.过点O作OE⊥OP交PB的延长线于E.
(1)探究BE与PC之间的数量关系,并说明理由.
(2)BP、CP、OP三者之间存在怎样的关系?并说明理由.
18.如图,在正方形ABCD中,点P在AD上,且不与A,D重合,点H在AB上,且不与A,B重合,连接BP、CH,BP与CH交于点E.
(1)若BP=CH,求证:BP⊥CH;
(2)在(1)的条件下,若正方形ABCD的边长为12,AP=5,求线段CE的长.
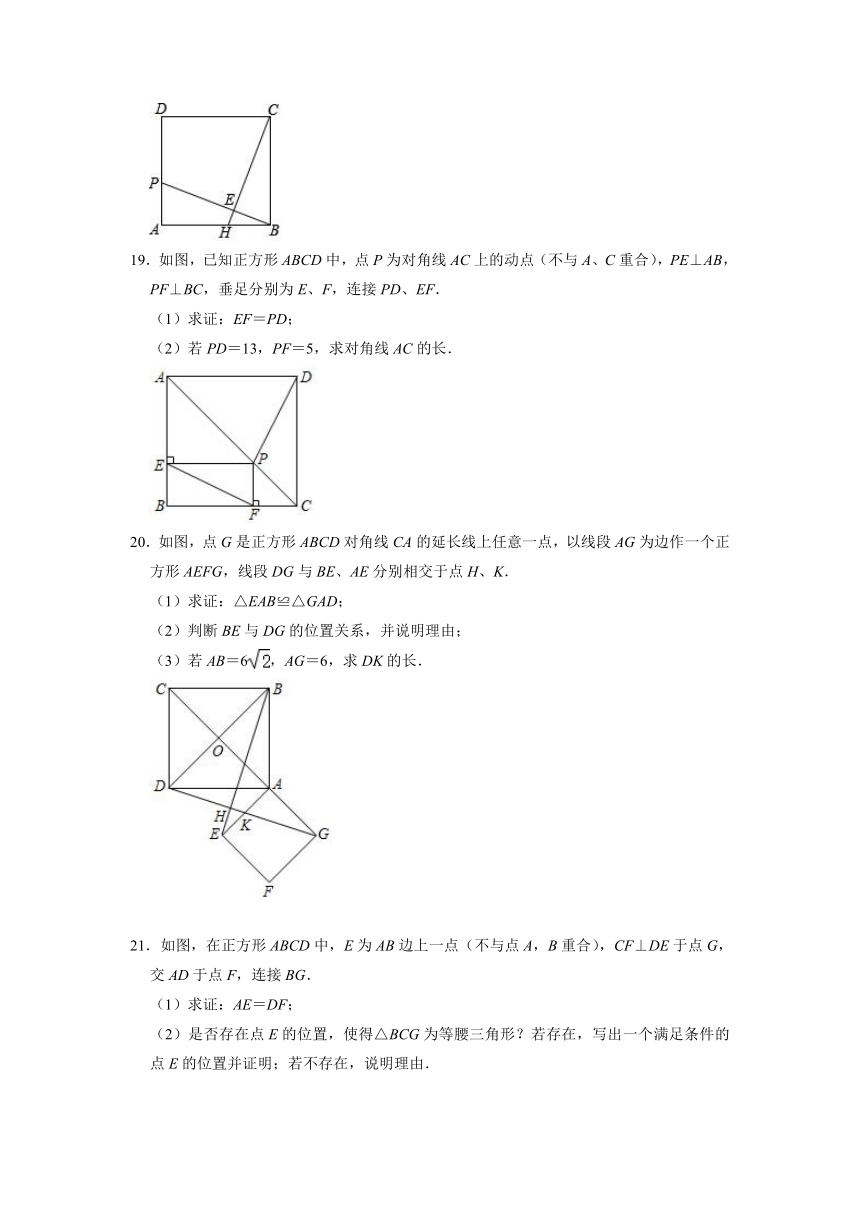
19.如图,已知正方形ABCD中,点P为对角线AC上的动点(不与A、C重合),PE⊥AB,PF⊥BC,垂足分别为E、F,连接PD、EF.
(1)求证:EF=PD;
(2)若PD=13,PF=5,求对角线AC的长.
20.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
21.如图,在正方形ABCD中,E为AB边上一点(不与点A,B重合),CF⊥DE于点G,交AD于点F,连接BG.
(1)求证:AE=DF;
(2)是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.
22.如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且AF=AD,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:AE=GE;
(2)求证:CG=DE.
23.如图,正方形ABCD中,点G是CD边上的一点(点G不与点C,点D重合),以CG为一边向正方形ABCD外做正方形GCEF,联结DE交BG的延长线于点H.
(1)求证:BH⊥DE;
(2)若正方形ABCD的边长为1,当点H为DE中点时,求CG的长.
参考答案
一.选择题(共8小题,每小题4分,共计32分)
1.解:如图,过点A作AH⊥AE,交CD的延长线于点H,
∵四边形ABCD是正方形,
∴AB=AD=CD=BC=6,∠BAD=∠ADC=90°,
∵AH⊥AE,
∴∠HAE=∠BAD=90°,
∴∠HAD=∠BAE,
在△ADH和△ABE中,
,
∴△ADH≌△ABE(ASA),
∴BE=HD,AH=AE,
∵∠EAF=45°,
∴∠HAF=∠EAF=45°,
在△AFH和△AFE中,
,
∴△AFH≌△AFE(SAS),
∴EF=HF,
∵DF=2,
∴CF=4,
∵EF2=CE2+CF2,
∴(2+BE)2=16+(6﹣BE)2,
∴BE=3,
∴HF=HD+DF=5,
∵△AFH≌△AFE,
∴S△AEF=S△AFH=×HF×AD=×5×6=15,
故选:C.
2.解:∵四边形ABCD为正方形,
∴OD=OB=OC,∠COD=90°,∠OCD=∠ODA=45°,
∵ON⊥OM,
∴∠MON=90°,
∵∠CON+∠DON=90°,∠DOM+∠DON=90°,
∴∠CON=∠DOM,
在△OCN和△ODM中,
,
∴△OCN≌△ODM(ASA),
∴S△OCN=S△ODM,
∴S△OCN+S△DON+S△ODM+S△DON,
即S△ODC=S四边形MOND=2,
∵OD?OC=2,
而OD=OC,
∴OD=2,
∴BD=2OD=4.
故选:D.
3.解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠A=∠ADC=∠DCB=∠B=90°,
∵DF⊥DE,
∴∠ADE+∠EDC=∠CDF+∠EDC,
即∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF,
∵E为AB的中点,AE=2,
∴AD=AB=4,
在Rt△ADE中,DE=,
在Rt△DEF中,EF=.
故选:B.
4.解:∵F、E分别是正方形ABCD的边AB与BC的中点,
∴AF=BE,
在△AFD和△BEA中,
,
∴△AFD≌△BEA(SAS),
∴∠FDA=∠EAB,
又∵∠FDA+∠AFD=90°,
∴∠EAB+∠AFD=90°,
即∠EAF+∠AFD=90°,
故C正确,A、B、D无法证明其成立,
故选:C.
5.解:如图,
∵顶点M、N的坐标分别为(﹣14,9)、(﹣5,9),
∴MN∥x轴,MN=9,BN∥y轴,
∴正方形的边长为3,
∴BN=6,
∴点B(﹣5,3),
∵AB∥MN,
∴AB∥x轴,
∴点A(﹣2,3),
故选:B.
6.解:过C点作CG⊥BD于G.
∵CF是∠DCE的平分线.
∴∠FCE=45°.
∵∠DBC=45°.
∴CF∥BD.
∴CG等于△PBD的高.
∵BD=2.
∴CG=1.
∴△PBD的面积等于.
故选:A.
7.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
8.解:由题意知,∵点F是CD的中点,∴DF=CF,
又∵∠D=∠FCM,∠DFA=∠CFM,
∴△ADF≌△MCF,
∴CM=AD=AB,
①正确;
设正方形ABCD边长为4,
∵CE=BC=1,
∴BE=3,
∴AE=5,
∴AE=AB+CE,
②正确;
EM=CM+CE=5=AE,
又∵F为AM的中点,
∴EF⊥AM,
④正确,
由CF=2,CE=1得EF=,
由DF=2,AD=4得AF=2,
∴S△AEF=5,
又S△ADF=4,
∴S四边形ABCF=S?ABCD﹣S△ADF=12,
③不正确,
故选:C.
二.填空题(共8小题,每小题4分,共计32分)
9.解:∵四边形ABCD为正方形,
∴CB=CD,∠BCD=90°,
∵CE=CB,
∴CD=CE,
∴∠CBE=∠CEB,∠CED=∠CDE,
∴∠CEB=(180°﹣∠BCE),∠CED=(180°﹣∠DCE),
∴∠CEB+∠CED=180°﹣(∠BCE+∠ECE),
即∠BED=180°﹣∠BCD,
∴∠BED=180°﹣×90°=135°.
故答案为135°.
10.解:如图,过点A作AB⊥x轴于B,过点D作DE⊥x轴于E,
∵四边形OACD是正方形,
∴OA=OD,∠AOD=90°,
∴∠DOE+∠AOB=90°,
又∵∠OAB+∠AOB=90°,
∴∠OAB=∠DOE,
在△AOD和△OCE中,
,
∴△AOB≌△ODE(AAS),
∴AB=OE,OB=DE,
∵点D的坐标为(3,4),点C在第二象限,
∴点C的坐标为(﹣4,3).
故答案为:(﹣4,3).
11.解:如图,作GH过点E,且GH∥AB,
∵∠HBE+∠HEB=90°,∠HEB+∠GEF=90°,
∴∠HBE=∠GEF,
∵AC为正方形的对角线,
∴CH=EH,
∴HB=GE,
在△HBE和△GEF中,
,
∴△HBE≌△GEF(ASA),
∴GF=EH,
设EH=a,AF=6﹣2a,
,,
∵2S1=3S2,
∴6a=3(a2﹣9a+18),
解得a=2,
∴CE==2,
故答案为2.
12.解:∵四边形ABCD是正方形,△ABE是等边三角形,
∴AD=AB,AB=AE,∠DAB=90°,∠BAE=60°,∠DAC=∠BAC=45°,
∴AD=AE,∠DAE=150°,
∴∠ADE=∠AED=15°,
∴∠AFE=∠DAC+∠FDA=60°,
在△DAF和△BAF中,
,
∴△DAF≌△BAF(SAS),
∴∠ADF=∠ABF=15°,
∴∠AFB=180°﹣∠BAF﹣∠ABF=120°,
∴∠BFE=∠AFB﹣∠AFE=60°,
故答案为:60°.
13.解:以O为原点,垂直AB的直线为x轴,建立直角坐标系,如图:
∵正方形ABCD的边长为4,CE=2,DF=1,
∴E(4,﹣2),F(2,3),
∵G为EF的中点,
∴G(3,),
设直线OE解析式为y=kx,将E(4,﹣2)代入得:
﹣2=4k,解得k=﹣,
∴直线OE解析式为y=﹣x,
令x=2得y=﹣1,
∴H(2,﹣1),
∴GH==,
方法二:如下图,连接OF,过点O作OM⊥CD交CD于M,
∵O为正方形对角线AC和BD的交点,
∴OM=CM=DM=CE=2,易证△OHM≌△EHC,
∴点H、点G分别为OE、FE的中点,
∴GH为△OEF的中位线,
∴GH=OF,
在Rt△OMF中,由勾股定理可得OF===,
∴GH=OF=,
故答案为:.
14.解:过G作GM⊥CD于M,如图:
∵正方形ABCD,
∴∠B=∠BCD=∠D=90°,BC=CD=AD,
∵GM⊥CD,
∴四边形GBCM是矩形,
∴GM=BC=CD,CM=BG=1,∠GMH=90°=∠D,
∵GH⊥CF,
∴∠DCE=90°﹣∠FHM=∠MGH,
在△GMH和△CDE中,
,
∴△GMH≌△CDE(ASA),
∴HM=DE,
∵CH=4,
∴HM=CH﹣CM=3=DE,
∵E是AD边的中点,
∴AE=DE=3,
故答案为:3.
15.解:如图所示:
延长BA到B′,使B′A=AB,
PB+PQ=PB′+PQ,
当B′,P,Q三点共线时,PB′+PQ的值最小,
根据题意,圆外一点B′到圆上一点Q距离的最小值B′Q=CB′﹣2,
∵BC=AB=4,
∴BB′=8,
∴B′C===4,
B′Q=B′C﹣2=4﹣2,
∴PB′+PQ的值最小是4﹣2,
即PQ+PB的最小值是4﹣2,
故答案为:4﹣2.
16.解:如图,延长AE,BC交于点H,连接AG,设EG与AF交于点N,
∵E为CD中点,
∴DE=CE=2,
在△ADE和△HCE中,
,
∴△ADE≌△HCE(ASA),
∴AE=EH,AD=CH=4,
∵CF=1,
∴FH=FC+CH=5,BF=3,
∵AF===5,
∴AF=FH,
又∵AE=EH,
∴EF⊥AH,∠AFE=∠HFE,
又∵EG⊥AF,∠DCB=90°,
∴EC=EN=2=DE,
在Rt△ADE和Rt△ANE中,
∴Rt△ADE≌Rt△ANE(HL),
∴AD=AN=4=AB,
在Rt△AGN和Rt△AGB中,
,
∴Rt△AGN≌Rt△AGB(HL),
∴BG=GN,
∵EG2=EC2+CG2,
∴(2+BG)2=4+(4﹣BG)2,
∴BG=,
故答案为:.
三.解答题(共7小题,每小题8分,共计56分)
17.解:(1)BE=PC,理由如下:
如图,连接OB,
∵四边形ABCD是正方形,
∴OB=OC,OB⊥OC,
∵OE⊥OP,
∴∠EOP=∠BOC=90°,
∴∠EOB+∠BOP=∠POC+∠BOP,即∠EOB=∠POC,
∵OE⊥OP,BP⊥CP,
∴∠E+∠OPE=∠OPC+∠OPE=90°,
∴∠E=∠OPC,
在△BOE与△COP中,
,
∴△BOE≌△COP(AAS),
∴BE=PC;
(2)BP+CP=OP,理由如下:
由(1)知,△BOE≌△COP,
∴BE=CP,OE=OP,
∴Rt△EOP是等腰直角三角形,
∴EP==OP,
∵EP=BP+BE=BP+CP,
∴BP+CP=OP.
18.(1)证明:∵四边形ABCD是正方形,
∴AB=AC=BC,∠A=∠ABC=90°,
在Rt△PAB和Rt△HBC中,
,
∴Rt△PAB≌Rt△HBC(HL),
∴∠APB=∠BHC,
∵∠APB+∠PBA=90°,
∴∠CHB+∠PBA=90°=∠CEB,
∴BP⊥CH;
(2)解:由(1)Rt△PAB≌Rt△HBC得BH=AP=5,
在Rt△HBC中,由勾股定理得:CH==13,
由△HBC的面积有:CH?BE=HB?BC,解得:BE=,
在Rt△EBC中,由勾股定理得CE==.
19.(1)证明:连接PB,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°,直线AC是正方形ABCD的对称轴,
∴PB=PD,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠PFB=∠ABC=90°,
∴四边形BEPF是矩形,
∴PB=EF,
∴EF=PD;
(2)解:由(1)知:EF=PD=13,
在Rt△PEF中,PE=,
∴PE=,
∵四边形ABCD是正方形,
∴△AEP是等腰直角三角形,
∴AE=PE=12,
∴AB=AE+BE=PE+PF=17=BC,
∴AC==.
20.(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
,
在Rt△ABC中,
∵AB=BC=6,
∴AC==12,
∴AO=DO=AC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK===3.
21.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°,
∴∠ADE+∠AED=90°,
∵CF⊥DE于点G,
∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴AE=DF;
(2)解:存在,当点E为AB的中点时,△BCG为等腰三角形,
理由:如图,延长CB交DE的延长线于点P,
∵E为AB的中点,
∴AE=BE,
在△AED和△BEP中,
,
∴△AED≌△BEP(ASA),
∴AD=BP=BC,
∵∠PGC=90°,
∴BG=CP=BC,
即△BCG为等腰三角形.
22.证明:(1)∵AF=AD,AE⊥DF,
∴∠DAE=∠EAF=∠DAF,
∵AF平分∠EAF,
∴∠BAG=∠FAG=∠BAF,
∵∠GAE=∠EAF﹣∠FAG=(∠DAF﹣∠BAF),
∴∠GAE=45°,
∴∠GAE=∠AGE=45°,
∴AE=GE;
(2)如图,过点C作CH⊥DF于H,
∴∠AED=∠CHD=90°,
∴∠ADE+∠EAD=90°=∠ADE+∠CDH,
∴∠EAD=∠CDH,
在△ADE和△DCH中,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=GE,
∴DE=GH=CH,
∴GC=CH=DE.
23.(1)证明:
∵正方形ABCD,
∴∠BCD=90°,BC=CD,
同理:CG=CE,
∠GCE=90°,
∴∠BCD=∠GCE=90°,
,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠CDE,
在Rt△DCE中∠CDE+∠CED=90°,
∴∠GBC+∠BEH=90°,
∴∠BHE=180°﹣(∠GBC+∠BEH)=90°,
∴BH⊥DE;
(2)连接BD,
∵点H为DE中点,BH⊥DE,
∴BH为DE的垂直平分线,
∴BE=BD,
∵BC=CD=1,
∴BD==,
∴BE=BD=,
∵CE=BE﹣BC=﹣1,
∴CG=CE=﹣1.
同步能力达标测评(附答案)
一.选择题(共8小题,每小题4分,共计32分)
1.如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,已知AD=6(正方形的四条边都相等,四个内角都是直角),DF=2,则S△AEF=( )
A.6
B.12
C.15
D.30
2.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是2,则BD的长为( )
A.
B.2
C.2
D.4
3.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作DF⊥DE交BC的延长线于点F,连结EF.若AE=2,则EF的值为( )
A.6
B.
C.
D.5
4.如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于P.则下列结论成立的是( )
A.BE=AE
B.PC=PD
C.∠EAF+∠AFD=90°
D.PE=EC
5.如图,将5个大小相同的正方形置于平面直角坐标系中,如果顶点M、N的坐标分别为(﹣14,9)、(﹣5,9),则顶点A的坐标为( )
A.(﹣3,2)
B.(﹣2,3)
C.(﹣2,2)
D.(﹣3,3)
6.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.1
B.
C.2
D.无法确定
7.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4
B.2
C.
D.2
8.如图,已知四边形ABCD是四个角都是直角,四条边都相等的正方形,点E在BC上,且CE=BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=;④∠AFE=90°,其中正确的结论的个数有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,每小题4分,共计32分)
9.如图,点E在正方形ABCD内,且EC=BC,则∠BED=
°.
10.如图,将正方形OACD放在平面直角坐标系中,O是坐标原点,点D的坐标为(3,4),则点A的坐标为
.
11.如图正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为
.
12.如图,正方形ABCD的右侧作等边△ABE,连接DE、AC交于点F,连接BF,则∠BFE=
.
13.如图,正方形ABCD的边长为4,对角线AC,BD相交于点O,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H,连接GH,则GH的长为
.
14.如图,在正方形ABCD中,点E是AD边的中点,连接CE,点F在CE上,过点F作CE的垂线,分别交AB,CD于点G,H.若BG=1,CH=4,则AE的长度为
.
15.如图,在边长为4的正方形ABCD中,E、F分别是边BC、DC上的动点,且EF=4,Q为EF中点,P是边AD上的一个动点,则PQ+PB的最小值是
.
16.如图,正方形ABCD的边长为4,E为CD中点,F为BC边上一点,且CF=1,连AF,EG⊥AF交BC于G,则BG=
.
三.解答题(共7小题,每小题8分,共计56分)
17.如图,正方形ABCD中,点O为对角线AC的中点,点P为平面内外一点,且BP⊥CP.过点O作OE⊥OP交PB的延长线于E.
(1)探究BE与PC之间的数量关系,并说明理由.
(2)BP、CP、OP三者之间存在怎样的关系?并说明理由.
18.如图,在正方形ABCD中,点P在AD上,且不与A,D重合,点H在AB上,且不与A,B重合,连接BP、CH,BP与CH交于点E.
(1)若BP=CH,求证:BP⊥CH;
(2)在(1)的条件下,若正方形ABCD的边长为12,AP=5,求线段CE的长.
19.如图,已知正方形ABCD中,点P为对角线AC上的动点(不与A、C重合),PE⊥AB,PF⊥BC,垂足分别为E、F,连接PD、EF.
(1)求证:EF=PD;
(2)若PD=13,PF=5,求对角线AC的长.
20.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
21.如图,在正方形ABCD中,E为AB边上一点(不与点A,B重合),CF⊥DE于点G,交AD于点F,连接BG.
(1)求证:AE=DF;
(2)是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.
22.如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且AF=AD,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:AE=GE;
(2)求证:CG=DE.
23.如图,正方形ABCD中,点G是CD边上的一点(点G不与点C,点D重合),以CG为一边向正方形ABCD外做正方形GCEF,联结DE交BG的延长线于点H.
(1)求证:BH⊥DE;
(2)若正方形ABCD的边长为1,当点H为DE中点时,求CG的长.
参考答案
一.选择题(共8小题,每小题4分,共计32分)
1.解:如图,过点A作AH⊥AE,交CD的延长线于点H,
∵四边形ABCD是正方形,
∴AB=AD=CD=BC=6,∠BAD=∠ADC=90°,
∵AH⊥AE,
∴∠HAE=∠BAD=90°,
∴∠HAD=∠BAE,
在△ADH和△ABE中,
,
∴△ADH≌△ABE(ASA),
∴BE=HD,AH=AE,
∵∠EAF=45°,
∴∠HAF=∠EAF=45°,
在△AFH和△AFE中,
,
∴△AFH≌△AFE(SAS),
∴EF=HF,
∵DF=2,
∴CF=4,
∵EF2=CE2+CF2,
∴(2+BE)2=16+(6﹣BE)2,
∴BE=3,
∴HF=HD+DF=5,
∵△AFH≌△AFE,
∴S△AEF=S△AFH=×HF×AD=×5×6=15,
故选:C.
2.解:∵四边形ABCD为正方形,
∴OD=OB=OC,∠COD=90°,∠OCD=∠ODA=45°,
∵ON⊥OM,
∴∠MON=90°,
∵∠CON+∠DON=90°,∠DOM+∠DON=90°,
∴∠CON=∠DOM,
在△OCN和△ODM中,
,
∴△OCN≌△ODM(ASA),
∴S△OCN=S△ODM,
∴S△OCN+S△DON+S△ODM+S△DON,
即S△ODC=S四边形MOND=2,
∵OD?OC=2,
而OD=OC,
∴OD=2,
∴BD=2OD=4.
故选:D.
3.解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠A=∠ADC=∠DCB=∠B=90°,
∵DF⊥DE,
∴∠ADE+∠EDC=∠CDF+∠EDC,
即∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF,
∵E为AB的中点,AE=2,
∴AD=AB=4,
在Rt△ADE中,DE=,
在Rt△DEF中,EF=.
故选:B.
4.解:∵F、E分别是正方形ABCD的边AB与BC的中点,
∴AF=BE,
在△AFD和△BEA中,
,
∴△AFD≌△BEA(SAS),
∴∠FDA=∠EAB,
又∵∠FDA+∠AFD=90°,
∴∠EAB+∠AFD=90°,
即∠EAF+∠AFD=90°,
故C正确,A、B、D无法证明其成立,
故选:C.
5.解:如图,
∵顶点M、N的坐标分别为(﹣14,9)、(﹣5,9),
∴MN∥x轴,MN=9,BN∥y轴,
∴正方形的边长为3,
∴BN=6,
∴点B(﹣5,3),
∵AB∥MN,
∴AB∥x轴,
∴点A(﹣2,3),
故选:B.
6.解:过C点作CG⊥BD于G.
∵CF是∠DCE的平分线.
∴∠FCE=45°.
∵∠DBC=45°.
∴CF∥BD.
∴CG等于△PBD的高.
∵BD=2.
∴CG=1.
∴△PBD的面积等于.
故选:A.
7.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
8.解:由题意知,∵点F是CD的中点,∴DF=CF,
又∵∠D=∠FCM,∠DFA=∠CFM,
∴△ADF≌△MCF,
∴CM=AD=AB,
①正确;
设正方形ABCD边长为4,
∵CE=BC=1,
∴BE=3,
∴AE=5,
∴AE=AB+CE,
②正确;
EM=CM+CE=5=AE,
又∵F为AM的中点,
∴EF⊥AM,
④正确,
由CF=2,CE=1得EF=,
由DF=2,AD=4得AF=2,
∴S△AEF=5,
又S△ADF=4,
∴S四边形ABCF=S?ABCD﹣S△ADF=12,
③不正确,
故选:C.
二.填空题(共8小题,每小题4分,共计32分)
9.解:∵四边形ABCD为正方形,
∴CB=CD,∠BCD=90°,
∵CE=CB,
∴CD=CE,
∴∠CBE=∠CEB,∠CED=∠CDE,
∴∠CEB=(180°﹣∠BCE),∠CED=(180°﹣∠DCE),
∴∠CEB+∠CED=180°﹣(∠BCE+∠ECE),
即∠BED=180°﹣∠BCD,
∴∠BED=180°﹣×90°=135°.
故答案为135°.
10.解:如图,过点A作AB⊥x轴于B,过点D作DE⊥x轴于E,
∵四边形OACD是正方形,
∴OA=OD,∠AOD=90°,
∴∠DOE+∠AOB=90°,
又∵∠OAB+∠AOB=90°,
∴∠OAB=∠DOE,
在△AOD和△OCE中,
,
∴△AOB≌△ODE(AAS),
∴AB=OE,OB=DE,
∵点D的坐标为(3,4),点C在第二象限,
∴点C的坐标为(﹣4,3).
故答案为:(﹣4,3).
11.解:如图,作GH过点E,且GH∥AB,
∵∠HBE+∠HEB=90°,∠HEB+∠GEF=90°,
∴∠HBE=∠GEF,
∵AC为正方形的对角线,
∴CH=EH,
∴HB=GE,
在△HBE和△GEF中,
,
∴△HBE≌△GEF(ASA),
∴GF=EH,
设EH=a,AF=6﹣2a,
,,
∵2S1=3S2,
∴6a=3(a2﹣9a+18),
解得a=2,
∴CE==2,
故答案为2.
12.解:∵四边形ABCD是正方形,△ABE是等边三角形,
∴AD=AB,AB=AE,∠DAB=90°,∠BAE=60°,∠DAC=∠BAC=45°,
∴AD=AE,∠DAE=150°,
∴∠ADE=∠AED=15°,
∴∠AFE=∠DAC+∠FDA=60°,
在△DAF和△BAF中,
,
∴△DAF≌△BAF(SAS),
∴∠ADF=∠ABF=15°,
∴∠AFB=180°﹣∠BAF﹣∠ABF=120°,
∴∠BFE=∠AFB﹣∠AFE=60°,
故答案为:60°.
13.解:以O为原点,垂直AB的直线为x轴,建立直角坐标系,如图:
∵正方形ABCD的边长为4,CE=2,DF=1,
∴E(4,﹣2),F(2,3),
∵G为EF的中点,
∴G(3,),
设直线OE解析式为y=kx,将E(4,﹣2)代入得:
﹣2=4k,解得k=﹣,
∴直线OE解析式为y=﹣x,
令x=2得y=﹣1,
∴H(2,﹣1),
∴GH==,
方法二:如下图,连接OF,过点O作OM⊥CD交CD于M,
∵O为正方形对角线AC和BD的交点,
∴OM=CM=DM=CE=2,易证△OHM≌△EHC,
∴点H、点G分别为OE、FE的中点,
∴GH为△OEF的中位线,
∴GH=OF,
在Rt△OMF中,由勾股定理可得OF===,
∴GH=OF=,
故答案为:.
14.解:过G作GM⊥CD于M,如图:
∵正方形ABCD,
∴∠B=∠BCD=∠D=90°,BC=CD=AD,
∵GM⊥CD,
∴四边形GBCM是矩形,
∴GM=BC=CD,CM=BG=1,∠GMH=90°=∠D,
∵GH⊥CF,
∴∠DCE=90°﹣∠FHM=∠MGH,
在△GMH和△CDE中,
,
∴△GMH≌△CDE(ASA),
∴HM=DE,
∵CH=4,
∴HM=CH﹣CM=3=DE,
∵E是AD边的中点,
∴AE=DE=3,
故答案为:3.
15.解:如图所示:
延长BA到B′,使B′A=AB,
PB+PQ=PB′+PQ,
当B′,P,Q三点共线时,PB′+PQ的值最小,
根据题意,圆外一点B′到圆上一点Q距离的最小值B′Q=CB′﹣2,
∵BC=AB=4,
∴BB′=8,
∴B′C===4,
B′Q=B′C﹣2=4﹣2,
∴PB′+PQ的值最小是4﹣2,
即PQ+PB的最小值是4﹣2,
故答案为:4﹣2.
16.解:如图,延长AE,BC交于点H,连接AG,设EG与AF交于点N,
∵E为CD中点,
∴DE=CE=2,
在△ADE和△HCE中,
,
∴△ADE≌△HCE(ASA),
∴AE=EH,AD=CH=4,
∵CF=1,
∴FH=FC+CH=5,BF=3,
∵AF===5,
∴AF=FH,
又∵AE=EH,
∴EF⊥AH,∠AFE=∠HFE,
又∵EG⊥AF,∠DCB=90°,
∴EC=EN=2=DE,
在Rt△ADE和Rt△ANE中,
∴Rt△ADE≌Rt△ANE(HL),
∴AD=AN=4=AB,
在Rt△AGN和Rt△AGB中,
,
∴Rt△AGN≌Rt△AGB(HL),
∴BG=GN,
∵EG2=EC2+CG2,
∴(2+BG)2=4+(4﹣BG)2,
∴BG=,
故答案为:.
三.解答题(共7小题,每小题8分,共计56分)
17.解:(1)BE=PC,理由如下:
如图,连接OB,
∵四边形ABCD是正方形,
∴OB=OC,OB⊥OC,
∵OE⊥OP,
∴∠EOP=∠BOC=90°,
∴∠EOB+∠BOP=∠POC+∠BOP,即∠EOB=∠POC,
∵OE⊥OP,BP⊥CP,
∴∠E+∠OPE=∠OPC+∠OPE=90°,
∴∠E=∠OPC,
在△BOE与△COP中,
,
∴△BOE≌△COP(AAS),
∴BE=PC;
(2)BP+CP=OP,理由如下:
由(1)知,△BOE≌△COP,
∴BE=CP,OE=OP,
∴Rt△EOP是等腰直角三角形,
∴EP==OP,
∵EP=BP+BE=BP+CP,
∴BP+CP=OP.
18.(1)证明:∵四边形ABCD是正方形,
∴AB=AC=BC,∠A=∠ABC=90°,
在Rt△PAB和Rt△HBC中,
,
∴Rt△PAB≌Rt△HBC(HL),
∴∠APB=∠BHC,
∵∠APB+∠PBA=90°,
∴∠CHB+∠PBA=90°=∠CEB,
∴BP⊥CH;
(2)解:由(1)Rt△PAB≌Rt△HBC得BH=AP=5,
在Rt△HBC中,由勾股定理得:CH==13,
由△HBC的面积有:CH?BE=HB?BC,解得:BE=,
在Rt△EBC中,由勾股定理得CE==.
19.(1)证明:连接PB,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°,直线AC是正方形ABCD的对称轴,
∴PB=PD,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠PFB=∠ABC=90°,
∴四边形BEPF是矩形,
∴PB=EF,
∴EF=PD;
(2)解:由(1)知:EF=PD=13,
在Rt△PEF中,PE=,
∴PE=,
∵四边形ABCD是正方形,
∴△AEP是等腰直角三角形,
∴AE=PE=12,
∴AB=AE+BE=PE+PF=17=BC,
∴AC==.
20.(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
,
在Rt△ABC中,
∵AB=BC=6,
∴AC==12,
∴AO=DO=AC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK===3.
21.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°,
∴∠ADE+∠AED=90°,
∵CF⊥DE于点G,
∴∠ADE+∠DFC=90°,
∴∠AED=∠DFC,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴AE=DF;
(2)解:存在,当点E为AB的中点时,△BCG为等腰三角形,
理由:如图,延长CB交DE的延长线于点P,
∵E为AB的中点,
∴AE=BE,
在△AED和△BEP中,
,
∴△AED≌△BEP(ASA),
∴AD=BP=BC,
∵∠PGC=90°,
∴BG=CP=BC,
即△BCG为等腰三角形.
22.证明:(1)∵AF=AD,AE⊥DF,
∴∠DAE=∠EAF=∠DAF,
∵AF平分∠EAF,
∴∠BAG=∠FAG=∠BAF,
∵∠GAE=∠EAF﹣∠FAG=(∠DAF﹣∠BAF),
∴∠GAE=45°,
∴∠GAE=∠AGE=45°,
∴AE=GE;
(2)如图,过点C作CH⊥DF于H,
∴∠AED=∠CHD=90°,
∴∠ADE+∠EAD=90°=∠ADE+∠CDH,
∴∠EAD=∠CDH,
在△ADE和△DCH中,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=GE,
∴DE=GH=CH,
∴GC=CH=DE.
23.(1)证明:
∵正方形ABCD,
∴∠BCD=90°,BC=CD,
同理:CG=CE,
∠GCE=90°,
∴∠BCD=∠GCE=90°,
,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠CDE,
在Rt△DCE中∠CDE+∠CED=90°,
∴∠GBC+∠BEH=90°,
∴∠BHE=180°﹣(∠GBC+∠BEH)=90°,
∴BH⊥DE;
(2)连接BD,
∵点H为DE中点,BH⊥DE,
∴BH为DE的垂直平分线,
∴BE=BD,
∵BC=CD=1,
∴BD==,
∴BE=BD=,
∵CE=BE﹣BC=﹣1,
∴CG=CE=﹣1.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
