24.3一元二次方程根与系数的关系 冀教版数学九年级上册课件(18张)
文档属性
| 名称 | 24.3一元二次方程根与系数的关系 冀教版数学九年级上册课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 607.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 09:56:13 | ||
图片预览





文档简介
(共18张PPT)
一元二次方程根与系数的关系
24.3
学习目标
1、经历一元二次方程根与系数的关系的探究过程,体会探究过程中体现的化归思想。
2、了解一元二次方程根与系数的关系,能用符号表示根与系数的关系。
3、应用一元二次方程中根与系数的关系,解决一些简单的问题。
复习引入
2.一元二次方程的根的情况怎样确定?
1.一元二次方程的求根公式是什么?
想一想:方程的两个根x1
,
x2与系数a,b,c还有其它关系吗?
1
自主探究
一元二次方程根与系数的关系
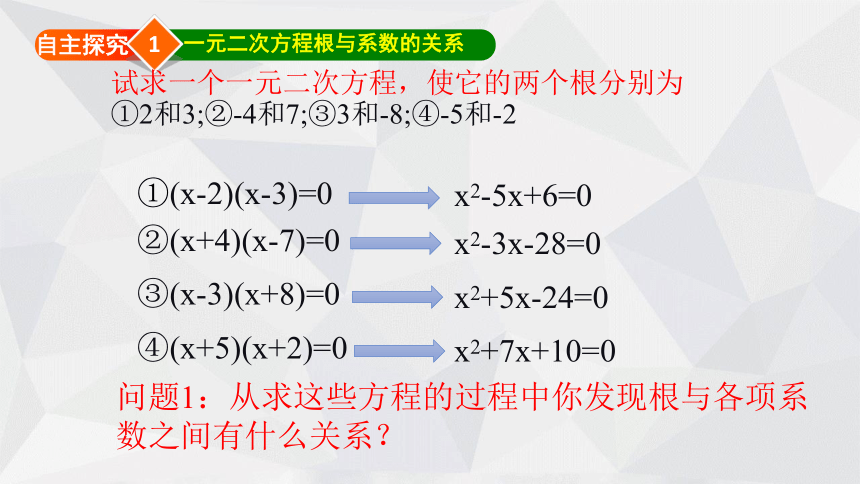
试求一个一元二次方程,使它的两个根分别为
①2和3;②-4和7;③3和-8;④-5和-2
问题1:从求这些方程的过程中你发现根与各项系数之间有什么关系?
x2-5x+6=0
①(x-2)(x-3)=0
x2-3x-28=0
②(x+4)(x-7)=0
③(x-3)(x+8)=0
x2+5x-24=0
④(x+5)(x+2)=0
x2+7x+10=0
总结:如果一元二次方程x2+px+q=0有两个根是x1
,
x2
那么有x1+
x2=
-p,
x1
?x2=
q
方程
两个根
两根之和
两根之积
x1
x2
x1+
x2
x1
?x2
x2-5x+6=0
2
3
5
6
x2-3x-28=0
-4
7
3
-28
x2+5x-24=0
3
-8
-5
-24
x2+7x+10=0
-5
-2
-7
10
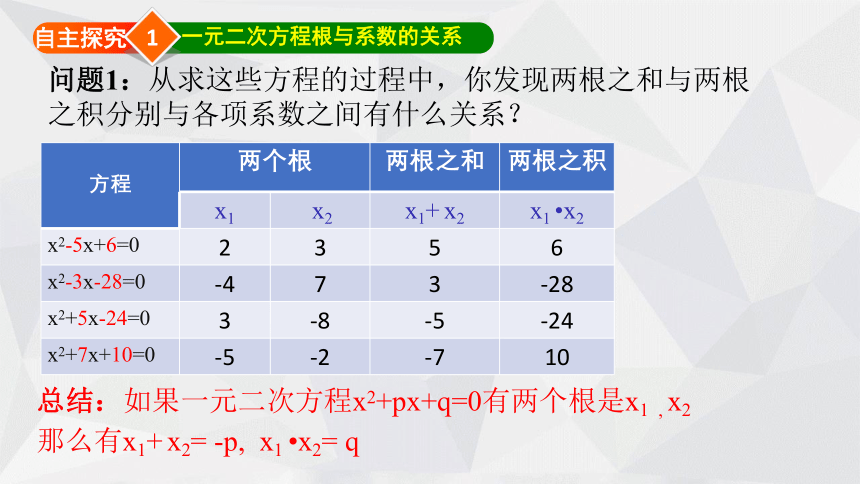
问题1:从求这些方程的过程中,你发现两根之和与两根之积分别与各项系数之间有什么关系?
1
自主探究
一元二次方程根与系数的关系
结论:如果一元二次方程x2+px+q=0有两个根是x1
,
x2
那么有x1+
x2=
-p,
x1
?x2=
q
2
合作探究
一元二次方程根与系数的关系
猜想1:2x2-5x+3=0(
x1=
,x2=1;
x1+
x2=
,
x1
?x2=
),这个方程的两根之和,两根之积分别与各项系数之间有什么关系?
猜想2:对于一元二次方程的一般式:
是否也有这样的结论?
若设它的两个根分别是x1
,
x2,
那么有x1+
x2=
__________,
x1
?
x2=
__________.
2
合作探究
一元二次方程根与系数的关系
设
是关于x的一元二次方程
的两个根.
试证明:(1)
(2)
2
合作探究
一元二次方程根与系数的关系
推导:
2
合作探究
一元二次方程根与系数的关系
推导:
如果一元二次方程
的两个根分别是
、
,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
概念:
?
?
16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
韦达(1540-1603)
数学名人传———韦达
例1
根据一元二次方程的根与系数的关系,求下列方程两个根的和与积:
(1)
x2-3x-8=0
(3)
2x2+5x=0
(5)
3x2=1
(2)
3x2+4x-7=0;
(4)
3x2-2x=-2
典例精析
注意:在使用一元二次方程根与系数的关系时,
(1)先将方程化成一般形式;(2)
判断
1、一元二次方程x2+4x-3=0的两根为x1,x2,则x1·x2的值是( )
A.4
B.-4
C.3
D.-3
2、已知x1、x2是方程x2+3x-1=0的两个实数根,那么下列结论正确的是( )
A.x1+x2=-1
B.x1+x2=-3
C.x1+x2=1
D.x1+x2=3
3、已知关于x的一元二次方程x2-x+4k=0有两个相等的实数根.
(1)求k的值.
(2)求两个根的和与积.
随堂练习
4、(1)已知方程x2+(k-1)x+3=0的两根之和为6
,
求k的值及方程的两根.
(2)已知方程x2+(k-1)x+
k2
=0的两根之积为1
,
求k的值.
随堂练习
当堂小结
请同学们谈谈本节课的收获与体会
本节课你学到了什么?
有什么收获?
课后作业
1、必做P46
练习1、习题A组
1
2、选做P46
习题B1
谢谢观看
结束
1
新知探究
一元二次方程根与系数的关系
例2、已知方程x2-x+4k=0有两个相等的实数根。
(1)求k的值。
(2)求两个根的和与积。
一元二次方程根与系数的关系
24.3
学习目标
1、经历一元二次方程根与系数的关系的探究过程,体会探究过程中体现的化归思想。
2、了解一元二次方程根与系数的关系,能用符号表示根与系数的关系。
3、应用一元二次方程中根与系数的关系,解决一些简单的问题。
复习引入
2.一元二次方程的根的情况怎样确定?
1.一元二次方程的求根公式是什么?
想一想:方程的两个根x1
,
x2与系数a,b,c还有其它关系吗?
1
自主探究
一元二次方程根与系数的关系
试求一个一元二次方程,使它的两个根分别为
①2和3;②-4和7;③3和-8;④-5和-2
问题1:从求这些方程的过程中你发现根与各项系数之间有什么关系?
x2-5x+6=0
①(x-2)(x-3)=0
x2-3x-28=0
②(x+4)(x-7)=0
③(x-3)(x+8)=0
x2+5x-24=0
④(x+5)(x+2)=0
x2+7x+10=0
总结:如果一元二次方程x2+px+q=0有两个根是x1
,
x2
那么有x1+
x2=
-p,
x1
?x2=
q
方程
两个根
两根之和
两根之积
x1
x2
x1+
x2
x1
?x2
x2-5x+6=0
2
3
5
6
x2-3x-28=0
-4
7
3
-28
x2+5x-24=0
3
-8
-5
-24
x2+7x+10=0
-5
-2
-7
10
问题1:从求这些方程的过程中,你发现两根之和与两根之积分别与各项系数之间有什么关系?
1
自主探究
一元二次方程根与系数的关系
结论:如果一元二次方程x2+px+q=0有两个根是x1
,
x2
那么有x1+
x2=
-p,
x1
?x2=
q
2
合作探究
一元二次方程根与系数的关系
猜想1:2x2-5x+3=0(
x1=
,x2=1;
x1+
x2=
,
x1
?x2=
),这个方程的两根之和,两根之积分别与各项系数之间有什么关系?
猜想2:对于一元二次方程的一般式:
是否也有这样的结论?
若设它的两个根分别是x1
,
x2,
那么有x1+
x2=
__________,
x1
?
x2=
__________.
2
合作探究
一元二次方程根与系数的关系
设
是关于x的一元二次方程
的两个根.
试证明:(1)
(2)
2
合作探究
一元二次方程根与系数的关系
推导:
2
合作探究
一元二次方程根与系数的关系
推导:
如果一元二次方程
的两个根分别是
、
,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
概念:
?
?
16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
韦达(1540-1603)
数学名人传———韦达
例1
根据一元二次方程的根与系数的关系,求下列方程两个根的和与积:
(1)
x2-3x-8=0
(3)
2x2+5x=0
(5)
3x2=1
(2)
3x2+4x-7=0;
(4)
3x2-2x=-2
典例精析
注意:在使用一元二次方程根与系数的关系时,
(1)先将方程化成一般形式;(2)
判断
1、一元二次方程x2+4x-3=0的两根为x1,x2,则x1·x2的值是( )
A.4
B.-4
C.3
D.-3
2、已知x1、x2是方程x2+3x-1=0的两个实数根,那么下列结论正确的是( )
A.x1+x2=-1
B.x1+x2=-3
C.x1+x2=1
D.x1+x2=3
3、已知关于x的一元二次方程x2-x+4k=0有两个相等的实数根.
(1)求k的值.
(2)求两个根的和与积.
随堂练习
4、(1)已知方程x2+(k-1)x+3=0的两根之和为6
,
求k的值及方程的两根.
(2)已知方程x2+(k-1)x+
k2
=0的两根之积为1
,
求k的值.
随堂练习
当堂小结
请同学们谈谈本节课的收获与体会
本节课你学到了什么?
有什么收获?
课后作业
1、必做P46
练习1、习题A组
1
2、选做P46
习题B1
谢谢观看
结束
1
新知探究
一元二次方程根与系数的关系
例2、已知方程x2-x+4k=0有两个相等的实数根。
(1)求k的值。
(2)求两个根的和与积。
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
