21.3实际问题与一元二次方程--面积问题 人教版数学九年级上册课件(19张)
文档属性
| 名称 | 21.3实际问题与一元二次方程--面积问题 人教版数学九年级上册课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
----面积问题
21.3实际问题与一元二次方程
列方程解应用题有哪些步骤?
即审、设、列、解、检、答。
上一节,我们学习了用方程解决
“平均增长(下降)率问题”,
现在,
我们要学习解决“面积问题。
例1、
要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
探究新知1
27
21
分析:这本书的长宽之比是9:7,依题知正中央的矩形两边之比也为9:7
解法一:设正中央的矩形两边分别为9xcm,7xcm
依题意得
解得
故上下边衬的宽度为:
左右边衬的宽度为:
分析:这本书的长宽之比是9:7,正中央的矩形两边之比也为9:7,由此判断上下边衬与左右边衬的宽度之比也为9:7
解法二:设上下边衬的宽为9xcm,左右边衬宽为7xcm,依题意得
解方程得
(以下同学们自己完成)
方程的哪个根合乎实际意义?为什么?
要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
探究新知
用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.
解:设这个矩形的长为xcm,则宽为
cm,
即
x2-10x+30=0
这里a=1,b=-10,c=30,
∴此方程无解.
∴用20cm长的铁丝不能折成面积为30cm2的矩形.
巩固练习
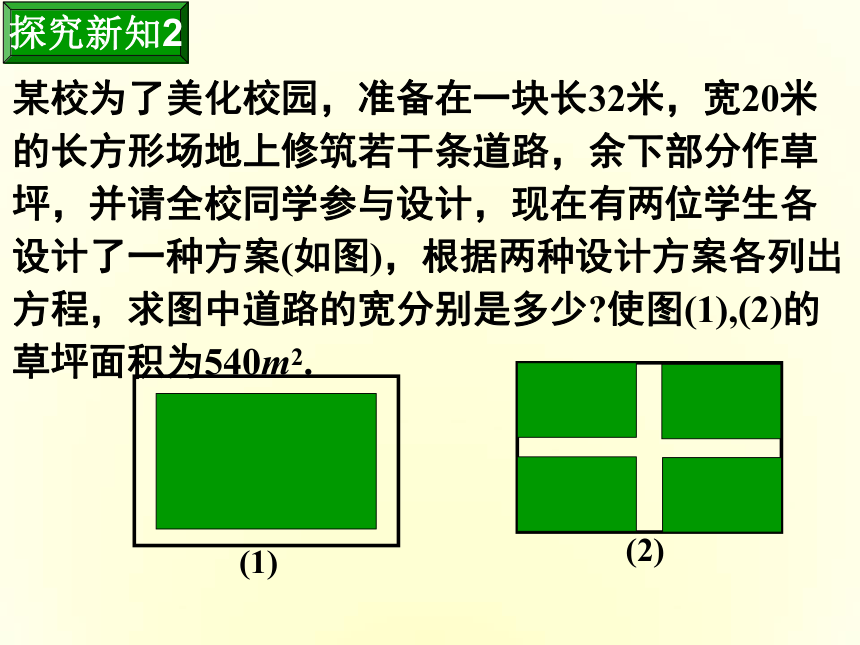
某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少?使图(1),(2)的草坪面积为540m2.
(1)
(2)
探究新知2
(1)
解:(1)如图,设道路的宽为x米,则
化简得,
其中的
x=25超出了原矩形的宽,应舍去.
∴图(1)中道路的宽为1米.
例题精讲
x
32
20
则横向的路面面积为
,
分析:此题的相等关系是矩形面积减去道路面积等于540m2。
解法一、
如图,设道路的宽为x米,
32x
m2
纵向的路面面积为
。
20x
m2
注意:这两个面积的重叠部分是
x2m2
所列的方程是不是
?
图中的道路面积不是
m2。
(2)
例题精讲
x
x
32
20
而是从其中减去重叠部分,即应是
m2
所以正确的方程是:
化简得,
其中的
x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:
=100
(m2)
草坪面积=
=
540(m2)
答:所求道路的宽为2m。
解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
发散思维
横向路面积
,
如图,设路宽为x米,
32xm2
纵向路面面积为
。
20xm2
草坪矩形的长(横向)为
,
草坪矩形的宽(纵向)
。
相等关系是:草坪长×草坪宽=540m2
(20-x)m
(32-x)m
即
化简得:
再往下的计算、格式书写与解法1相同。
活学活用
2.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
解:设道路宽为x米,
则
化简得,
x=35超出了原矩形的宽,舍去.
答:道路的宽为1米.
针对练习
在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是
(
)
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0
D.x2-65x-350=0
80cm
x
x
x
x
50cm
学以致用
B
有关面积问题:
常见的图形有下列几种:
这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求.
课堂小结
审、设、列、解、检、答。
熟记列方程解应用题的步骤
1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【
】
A.400cm2
B.500cm2
C.600cm2
D.4000cm2
A
课后检测
2、如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为
.
15m,10
m
或
20m,
7.5m
作业
1.完成教材P22第8.9题
2.课件的课后作业部分
谢谢
无数事实证明,任何人的任何一点成就,都是从勤学、勤思、勤问中得来的。
——夏衍
如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S平方米,(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?
【解析】(1)设宽AB为x米,
则BC为(24-3x)米,这时面积
S=x(24-3x)=-3x2+24x
(2)由条件-3x2+24x=45
化为:x2-8x+15=0解得x1=5,x2=3
∵0<24-3x≤10得
≤x<8
∴x2不合题意,AB=5,即花圃的宽AB为5米
强化训练
----面积问题
21.3实际问题与一元二次方程
列方程解应用题有哪些步骤?
即审、设、列、解、检、答。
上一节,我们学习了用方程解决
“平均增长(下降)率问题”,
现在,
我们要学习解决“面积问题。
例1、
要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
探究新知1
27
21
分析:这本书的长宽之比是9:7,依题知正中央的矩形两边之比也为9:7
解法一:设正中央的矩形两边分别为9xcm,7xcm
依题意得
解得
故上下边衬的宽度为:
左右边衬的宽度为:
分析:这本书的长宽之比是9:7,正中央的矩形两边之比也为9:7,由此判断上下边衬与左右边衬的宽度之比也为9:7
解法二:设上下边衬的宽为9xcm,左右边衬宽为7xcm,依题意得
解方程得
(以下同学们自己完成)
方程的哪个根合乎实际意义?为什么?
要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
探究新知
用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.
解:设这个矩形的长为xcm,则宽为
cm,
即
x2-10x+30=0
这里a=1,b=-10,c=30,
∴此方程无解.
∴用20cm长的铁丝不能折成面积为30cm2的矩形.
巩固练习
某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少?使图(1),(2)的草坪面积为540m2.
(1)
(2)
探究新知2
(1)
解:(1)如图,设道路的宽为x米,则
化简得,
其中的
x=25超出了原矩形的宽,应舍去.
∴图(1)中道路的宽为1米.
例题精讲
x
32
20
则横向的路面面积为
,
分析:此题的相等关系是矩形面积减去道路面积等于540m2。
解法一、
如图,设道路的宽为x米,
32x
m2
纵向的路面面积为
。
20x
m2
注意:这两个面积的重叠部分是
x2m2
所列的方程是不是
?
图中的道路面积不是
m2。
(2)
例题精讲
x
x
32
20
而是从其中减去重叠部分,即应是
m2
所以正确的方程是:
化简得,
其中的
x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:
=100
(m2)
草坪面积=
=
540(m2)
答:所求道路的宽为2m。
解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
发散思维
横向路面积
,
如图,设路宽为x米,
32xm2
纵向路面面积为
。
20xm2
草坪矩形的长(横向)为
,
草坪矩形的宽(纵向)
。
相等关系是:草坪长×草坪宽=540m2
(20-x)m
(32-x)m
即
化简得:
再往下的计算、格式书写与解法1相同。
活学活用
2.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
解:设道路宽为x米,
则
化简得,
x=35超出了原矩形的宽,舍去.
答:道路的宽为1米.
针对练习
在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是
(
)
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0
D.x2-65x-350=0
80cm
x
x
x
x
50cm
学以致用
B
有关面积问题:
常见的图形有下列几种:
这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求.
课堂小结
审、设、列、解、检、答。
熟记列方程解应用题的步骤
1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【
】
A.400cm2
B.500cm2
C.600cm2
D.4000cm2
A
课后检测
2、如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为
.
15m,10
m
或
20m,
7.5m
作业
1.完成教材P22第8.9题
2.课件的课后作业部分
谢谢
无数事实证明,任何人的任何一点成就,都是从勤学、勤思、勤问中得来的。
——夏衍
如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S平方米,(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?
【解析】(1)设宽AB为x米,
则BC为(24-3x)米,这时面积
S=x(24-3x)=-3x2+24x
(2)由条件-3x2+24x=45
化为:x2-8x+15=0解得x1=5,x2=3
∵0<24-3x≤10得
≤x<8
∴x2不合题意,AB=5,即花圃的宽AB为5米
强化训练
同课章节目录
