5.2.2同角三角函数的基本关系式课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共24张PPT)
文档属性
| 名称 | 5.2.2同角三角函数的基本关系式课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共24张PPT) | 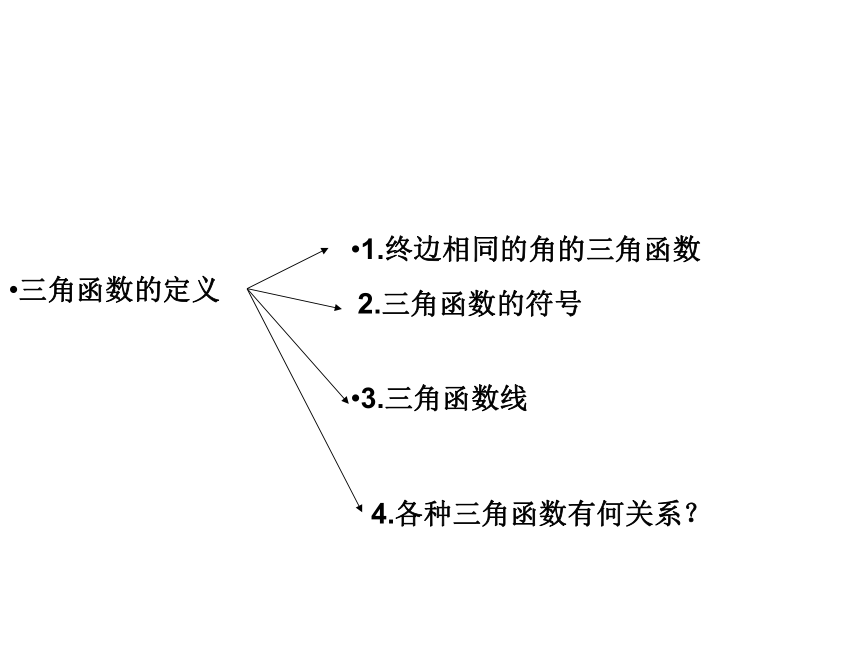 | |
| 格式 | ppt | ||
| 文件大小 | 484.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:32:16 | ||
图片预览








文档简介
(共24张PPT)
三角函数的定义
3.三角函数线
2.三角函数的符号
1.终边相同的角的三角函数
4.各种三角函数有何关系?
三者之间有哪些关系式成立?
同角三角函数的两个基本关系式:
1、平方关系:
2、商数关系:
除非特殊注明外,假定三角恒等式是在使两边都意义的情况下的恒等式!
公式特点:
(1)角:同角不同名;
(2)函数名称:切弦互化;
(3)结构:平方关系、商数关系。
公式含有的变形技巧:
(1)1代换;
(2)变名:切弦互化;
(3)升降次数.
1.“同角”的概念与角的表达形式无关.
2.三种关系式(公式)都必须在定义域允许的范围内成立.
3.
是
的简写,读作
的平方,
不能写成
已知角,求三角函数值
注意:涉及开方运算时,要由角的终边位置判断三角值符号.
方法1:变结构:先化简结构,再由角求值;
方法2:变角:由角求三角值,再计算求值.
已知一个角的一种三角值角,求这个角
课本21页12
已知一个角的某一个三角值,求这个角的其它两个三角函数值:
注意:
(1)涉及开方运算时,要由角的终边位置判断三角值符号.
(2)小题可把角看作锐角,借助直角三角形求,再由角的终边位置确定三角值的符号.
3:已知
,求
的值.
解:
(1)当
时
(2)当
时
由三角值符号判断角的终边位置
已知一个角的某一个三角值,求这个角的其它两个三角函数值:
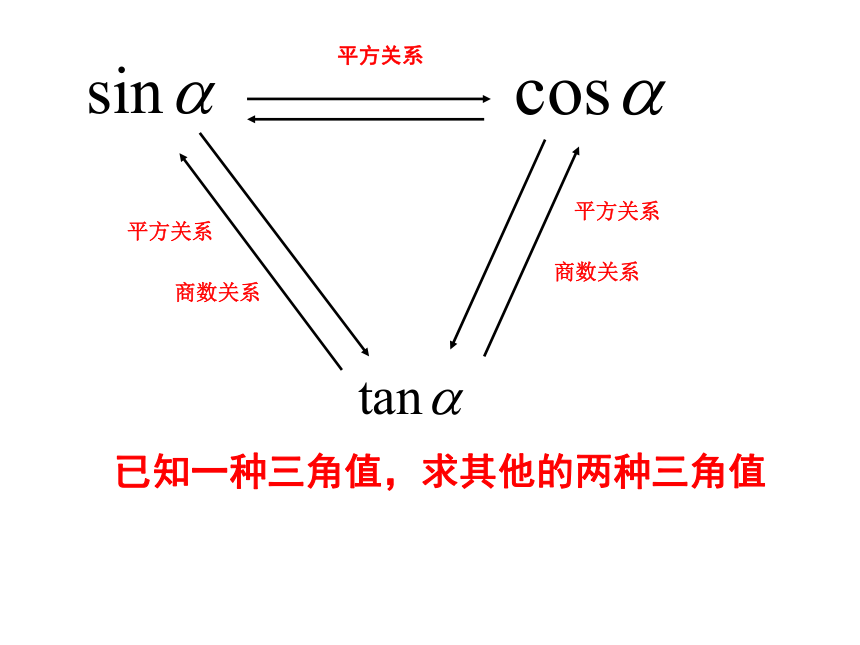
已知一种三角值,求其他的两种三角值
平方关系
平方关系
平方关系
商数关系
商数关系
(1)
(2)
平方、配方、整体代换、解方程.
方法1:特殊化、三角函数线.
方法2:平方、整体代换
平方、配方、整体代换、解方程.
关于化简:化简后的简单三角函数式应尽量满足以下几点:
(1)所含的三角函数种类最少;
(2)能求值的尽量求值;
(3)结果的次数最低.
课本20页4(2)
课本22页1
课本20页5(2)
分析方法:
1.证明等式:从一边到另一边,由繁到简.
2.证明三角等式:分析两边差异(角、名、结构):分母变名.
1.求证:
变用公式
课本19页例7
分析方法:
1.证明等式:从一边到另一边,由繁到简.
2.证明三角等式:分析两边差异(角、名、结构):切化弦、差化积
2.证明:
课本22页13(2)
证明恒等式的过程实质上就是分析、转化和消去等式两边差异(角、函数名、结构)来促成统一的过程:
1.证明方法:
(1)由一边向另一边证;
(4)由公式直接推出。
(3)两面夹;
(2)左-右=0;或商为1
2.技巧:
课本22页13(1)
分析:切化弦、分式化整式.
分析一:两头凑;
分析二:1代换、切化弦
4:求证:
分析一:左边通分、约分;
分析二:变用平方关系、等比性质.
7.
(1)
课堂小结
(1)、平方关系:
(2)、商数关系:
1.两个关系:
2.应用:(技巧:1代换,弦切互化)
(1)求值;
(2)化简;
(3)
证明。
从函数名称,运算结构分析
布置作业:
1.课时作业;
2.预习《诱导公式》。
三角函数的定义
3.三角函数线
2.三角函数的符号
1.终边相同的角的三角函数
4.各种三角函数有何关系?
三者之间有哪些关系式成立?
同角三角函数的两个基本关系式:
1、平方关系:
2、商数关系:
除非特殊注明外,假定三角恒等式是在使两边都意义的情况下的恒等式!
公式特点:
(1)角:同角不同名;
(2)函数名称:切弦互化;
(3)结构:平方关系、商数关系。
公式含有的变形技巧:
(1)1代换;
(2)变名:切弦互化;
(3)升降次数.
1.“同角”的概念与角的表达形式无关.
2.三种关系式(公式)都必须在定义域允许的范围内成立.
3.
是
的简写,读作
的平方,
不能写成
已知角,求三角函数值
注意:涉及开方运算时,要由角的终边位置判断三角值符号.
方法1:变结构:先化简结构,再由角求值;
方法2:变角:由角求三角值,再计算求值.
已知一个角的一种三角值角,求这个角
课本21页12
已知一个角的某一个三角值,求这个角的其它两个三角函数值:
注意:
(1)涉及开方运算时,要由角的终边位置判断三角值符号.
(2)小题可把角看作锐角,借助直角三角形求,再由角的终边位置确定三角值的符号.
3:已知
,求
的值.
解:
(1)当
时
(2)当
时
由三角值符号判断角的终边位置
已知一个角的某一个三角值,求这个角的其它两个三角函数值:
已知一种三角值,求其他的两种三角值
平方关系
平方关系
平方关系
商数关系
商数关系
(1)
(2)
平方、配方、整体代换、解方程.
方法1:特殊化、三角函数线.
方法2:平方、整体代换
平方、配方、整体代换、解方程.
关于化简:化简后的简单三角函数式应尽量满足以下几点:
(1)所含的三角函数种类最少;
(2)能求值的尽量求值;
(3)结果的次数最低.
课本20页4(2)
课本22页1
课本20页5(2)
分析方法:
1.证明等式:从一边到另一边,由繁到简.
2.证明三角等式:分析两边差异(角、名、结构):分母变名.
1.求证:
变用公式
课本19页例7
分析方法:
1.证明等式:从一边到另一边,由繁到简.
2.证明三角等式:分析两边差异(角、名、结构):切化弦、差化积
2.证明:
课本22页13(2)
证明恒等式的过程实质上就是分析、转化和消去等式两边差异(角、函数名、结构)来促成统一的过程:
1.证明方法:
(1)由一边向另一边证;
(4)由公式直接推出。
(3)两面夹;
(2)左-右=0;或商为1
2.技巧:
课本22页13(1)
分析:切化弦、分式化整式.
分析一:两头凑;
分析二:1代换、切化弦
4:求证:
分析一:左边通分、约分;
分析二:变用平方关系、等比性质.
7.
(1)
课堂小结
(1)、平方关系:
(2)、商数关系:
1.两个关系:
2.应用:(技巧:1代换,弦切互化)
(1)求值;
(2)化简;
(3)
证明。
从函数名称,运算结构分析
布置作业:
1.课时作业;
2.预习《诱导公式》。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
