1.4.2用空间向量研究距离、夹角问题(第2课时) 课件——2021-2022学年高二数学上学期人教A版(2019)选择性必修第一册(17张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题(第2课时) 课件——2021-2022学年高二数学上学期人教A版(2019)选择性必修第一册(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览


文档简介
人教A版(2019)选择性必修第一册
第一章 空间向量与立体几何
1.4.2 用空间向量研究距离、夹角问题
(第2课时)
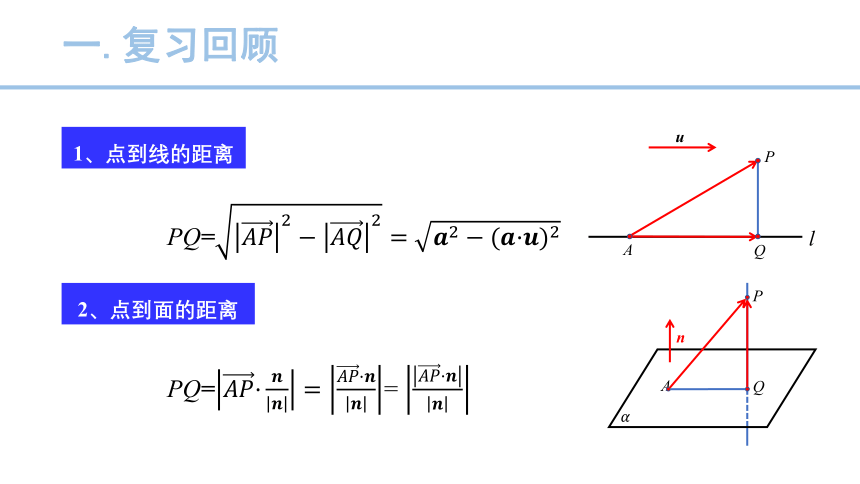
一.复习回顾
1、点到线的距离
2、点到面的距离
PQ=????????2?????????2= ????2?(????·????)2
?
PQ=????????·???????? =????????·????????= ????????·????????
?
l
A
u
Q
P
????
?
n
P
A
Q
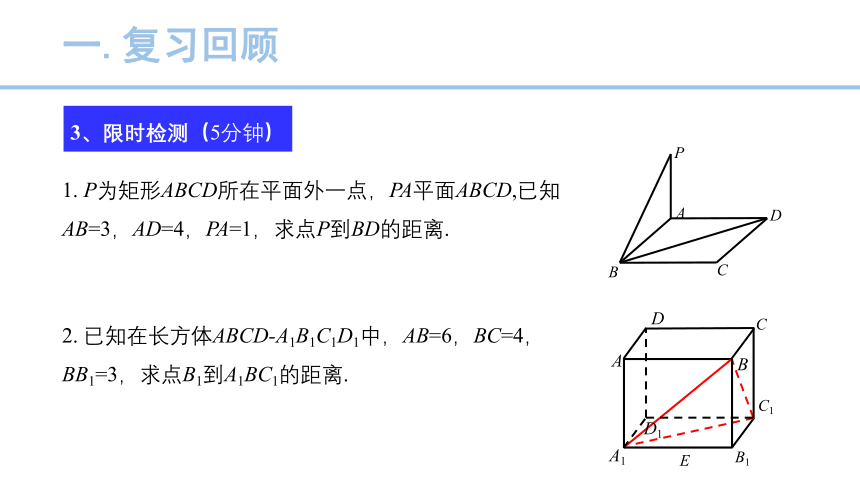
一.复习回顾
3、限时检测(5分钟)
1. P为矩形ABCD所在平面外一点,PA平面ABCD,已知AB=3,AD=4,PA=1,求点P到BD的距离.
P
B
C
D
A
2. 已知在长方体ABCD-A1B1C1D1中,AB=6,BC=4,BB1=3,求点B1到A1BC1的距离.
C
D
A
B
D1
A1
C1
B1
E
二.探究新知
如何用向量方法解决两条异面直线之间的夹角问题?
探究1
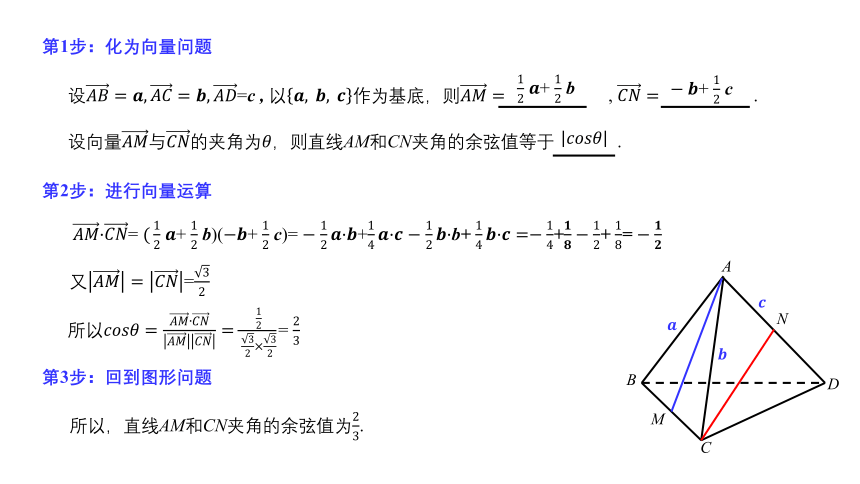
例7.如图,在棱长为1的正四面体ABCD中,M,N分别是BC,AD的中点,求直线AM
和CN夹角的余弦值.
A
B
C
D
N
M
分析:
直线AM和CN夹角的余弦值
直线????????和?????????夹角的余弦值
?
第1步:化为向量问题
第2步:进行向量运算
????????·????????= (12 ????+ 12 b)(?????+ 12 c)= ? 12????·????+14????·???? ? 12????·b+ 14????·????=?14+?????????12+ 18= ?????????
?
A
B
C
D
N
M
????
?
????
?
????
?
又????????=????????=32
?
所以????????????????=?????????????????????????????????=1232×32= 23
?
第3步:回到图形问题
所以,直线AM和CN夹角的余弦值为23.
?
12 ????+ 12 b
?
设????????=????,????????=????,????????=c , 以????,?????,?????作为基底,则????????= , ????????= .
?
设向量????????与????????的夹角为????,则直线AM和CN夹角的余弦值等于 .
?
??????+ 12 c
?
????????????????
?
l1
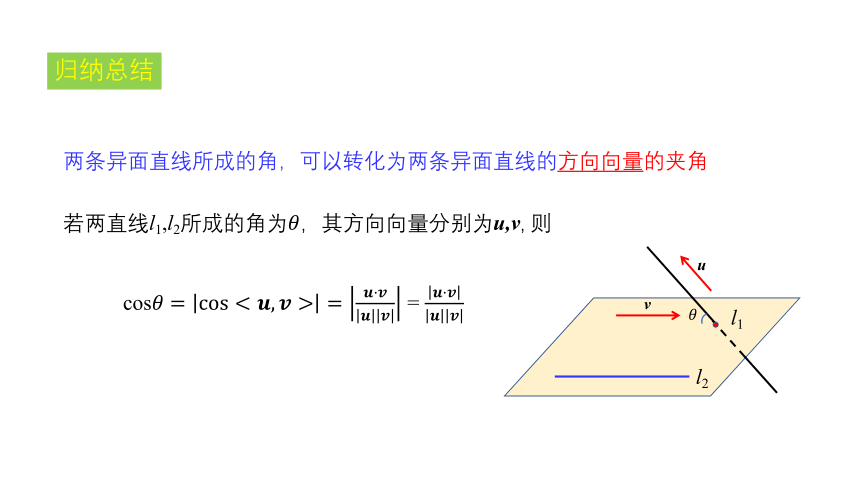
归纳总结
两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角
若两直线l1,l2所成的角为????,其方向向量分别为u,v, 则
?
l2
u
v
????
?
cos????=cos=????·???????????? = ????·????????????
?
????
?
n
B
A
C
如何用向量方法求直线 l 和平面?????的夹角?
?
探究2
直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
u
????
?
sin????=cos=????·???????????? = ????·????????????
?
若直线AB的方向向量为u,平面????的法向量为n,直线与平面的夹角为????,则
?
????
?
????
?
n1
如何用向量方法求平面????和平面????的夹角?
?
探究3
n2
平面与平面所成的角,可以转化为法向量与法向量的夹角.
若平面????,????的法向量分别为n1和n2,
?
cos????=cos=????1·????2????1????2 = ????1·????2????1????2
?
则平面????与平面????的夹角即为向量n1和n2的夹角或其补角.
?
设平面????与平面????的夹角为????,则
?
三.典例剖析
例8. 如图,在直三棱柱ABC-?A1B1C1中,AC=CB=2, AA1=3 ,∠????????????=90?,P为BC的中点,点Q, R分别在AA1, BB1上,A1Q =2AQ, BR =2RB1. 求平面PQR与平面?A1B1C1夹角的余弦值.
?
C
A
B
A1
C1
B1
F
Q
分析:因为平面与平面所成的角,可以转化为法向量与法向量的夹角.所以只需要求出两个平面的法向量的夹角即可.
P
R
第1步:化为向量问题
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
第2步:进行向量运算
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
第3步:回到图形问题
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
练习
四.课堂小结
1、直线与直线的夹角
2、直线与平面的夹角
cos????=cos=????·???????????? = ????·????????????
?
sin????=cos=????·???????????? = ????·????????????
?
3、平面与平面的夹角
cos????=cos=????1·????2????1????2 = ????1·????2????1????2
?
l1
l2
u
v
????
?
n
B
A
C
u
????
?
????
?
????
?
n1
n2
五.作业布置
【课堂作业】
教材P43 T9、T10
【课时作业】
必做题:
选做题:其他
第一章 空间向量与立体几何
1.4.2 用空间向量研究距离、夹角问题
(第2课时)
一.复习回顾
1、点到线的距离
2、点到面的距离
PQ=????????2?????????2= ????2?(????·????)2
?
PQ=????????·???????? =????????·????????= ????????·????????
?
l
A
u
Q
P
????
?
n
P
A
Q
一.复习回顾
3、限时检测(5分钟)
1. P为矩形ABCD所在平面外一点,PA平面ABCD,已知AB=3,AD=4,PA=1,求点P到BD的距离.
P
B
C
D
A
2. 已知在长方体ABCD-A1B1C1D1中,AB=6,BC=4,BB1=3,求点B1到A1BC1的距离.
C
D
A
B
D1
A1
C1
B1
E
二.探究新知
如何用向量方法解决两条异面直线之间的夹角问题?
探究1
例7.如图,在棱长为1的正四面体ABCD中,M,N分别是BC,AD的中点,求直线AM
和CN夹角的余弦值.
A
B
C
D
N
M
分析:
直线AM和CN夹角的余弦值
直线????????和?????????夹角的余弦值
?
第1步:化为向量问题
第2步:进行向量运算
????????·????????= (12 ????+ 12 b)(?????+ 12 c)= ? 12????·????+14????·???? ? 12????·b+ 14????·????=?14+?????????12+ 18= ?????????
?
A
B
C
D
N
M
????
?
????
?
????
?
又????????=????????=32
?
所以????????????????=?????????????????????????????????=1232×32= 23
?
第3步:回到图形问题
所以,直线AM和CN夹角的余弦值为23.
?
12 ????+ 12 b
?
设????????=????,????????=????,????????=c , 以????,?????,?????作为基底,则????????= , ????????= .
?
设向量????????与????????的夹角为????,则直线AM和CN夹角的余弦值等于 .
?
??????+ 12 c
?
????????????????
?
l1
归纳总结
两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角
若两直线l1,l2所成的角为????,其方向向量分别为u,v, 则
?
l2
u
v
????
?
cos????=cos=????·???????????? = ????·????????????
?
????
?
n
B
A
C
如何用向量方法求直线 l 和平面?????的夹角?
?
探究2
直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
u
????
?
sin????=cos=????·???????????? = ????·????????????
?
若直线AB的方向向量为u,平面????的法向量为n,直线与平面的夹角为????,则
?
????
?
????
?
n1
如何用向量方法求平面????和平面????的夹角?
?
探究3
n2
平面与平面所成的角,可以转化为法向量与法向量的夹角.
若平面????,????的法向量分别为n1和n2,
?
cos????=cos=????1·????2????1????2 = ????1·????2????1????2
?
则平面????与平面????的夹角即为向量n1和n2的夹角或其补角.
?
设平面????与平面????的夹角为????,则
?
三.典例剖析
例8. 如图,在直三棱柱ABC-?A1B1C1中,AC=CB=2, AA1=3 ,∠????????????=90?,P为BC的中点,点Q, R分别在AA1, BB1上,A1Q =2AQ, BR =2RB1. 求平面PQR与平面?A1B1C1夹角的余弦值.
?
C
A
B
A1
C1
B1
F
Q
分析:因为平面与平面所成的角,可以转化为法向量与法向量的夹角.所以只需要求出两个平面的法向量的夹角即可.
P
R
第1步:化为向量问题
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
第2步:进行向量运算
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
第3步:回到图形问题
C
z
A
B
A1
C1
x
y
B1
F
Q
P
R
练习
四.课堂小结
1、直线与直线的夹角
2、直线与平面的夹角
cos????=cos=????·???????????? = ????·????????????
?
sin????=cos=????·???????????? = ????·????????????
?
3、平面与平面的夹角
cos????=cos=????1·????2????1????2 = ????1·????2????1????2
?
l1
l2
u
v
????
?
n
B
A
C
u
????
?
????
?
????
?
n1
n2
五.作业布置
【课堂作业】
教材P43 T9、T10
【课时作业】
必做题:
选做题:其他
