圆与方程复习课教案-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册
文档属性
| 名称 | 圆与方程复习课教案-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:52:40 | ||
图片预览




文档简介
课题:§2
圆与方程复习课
目标要求
1、理解并掌握圆的方程的求法.
2、理解并掌握直线与圆的位置关系.
3、理解并掌握圆与圆的位置关系.
4、理解并掌握与圆有关的最值问题.
学科素养目标
本章以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.通过本章的学习,学生将在类比直线的研究方法的基础上,进一步体会和掌握在平面直角坐标系中建立圆的方程,进而运用方程研究圆的几何性质及直线和圆、圆和圆的相互位置关系,体会数形结合的思想,逐步形成用代数方法解决几何问题的能力.
重点难点
重点:两圆相交问题;
难点:圆与圆的综合应用问题.
教学过程
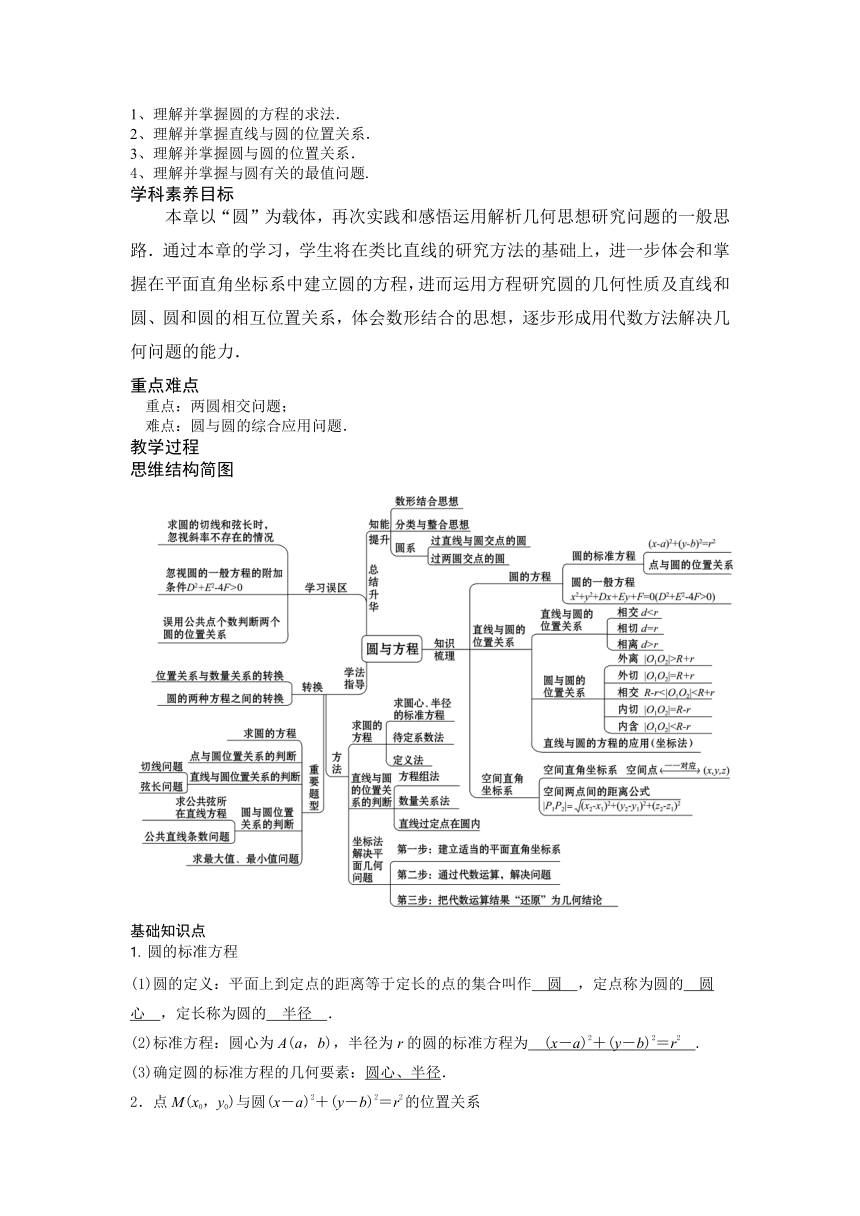
思维结构简图
基础知识点
1.
圆的标准方程
(1)圆的定义:平面上到定点的距离等于定长的点的集合叫作
__
,定点称为圆的
___
,定长称为圆的
_______
.
(2)标准方程:圆心为A(a,b),半径为r的圆的标准方程为
___________________
.
(3)确定圆的标准方程的几何要素:________________.
2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
(1)在圆内:(x0-a)2+(y0-b)2
_
r2或d
_
r;
(2)在圆上:(x0-a)2+(y0-b)2
_
r2或d
_
r;
(3)在圆外:(x0-a)2+(y0-b)2
r2或d
r.
3.
方程x2+y2+Dx+Ey+F=0表示的图形
将方程左边配方,并将常数项移到右边得+=
______
.
(1)当D2+E2-4F>0时,表示圆心为
_________
,半径为
________
的圆;
(2)当D2+E2-4F=0时,表示点
___________
;
(3)当D2+E2-4F<0时,不表示任何图形.
4.圆的一般方程
(1)一般方程:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0称为圆的
_____
方程.
(2)本质:圆的方程的另一种表示形式,更具有方程特征.
5.
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断:
(1)方法:
位置关系
相交
相切
相离
公共点个数
___个
1个
0个
方法
几何法:设圆心到直线的距离d=
d<r
_____
d>r
代数法:由消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
________
(2)本质:利用直线与圆的方程,通过定量计算研究直线与圆的位置关系.
6.
(1)若两圆的半径分别为r1,r2,圆心距为d,则两圆有以下位置关系:
位置关系
公共点个数
圆心距与半径的关系
图示
两圆外离
___
d
_
r1+r2
两圆内含
d
_
|r1-r2|
两圆相交
__
|r1-r2|
__
d
__
r1+r2
两圆内切
__
d
__
|r1-r2|
两圆外切
d
__
r1+r2
(2)本质:利用圆的方程,通过定量计算研究圆与圆的位置关系.
【课堂题组训练】
题组训练一 求圆的方程
题1.已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为( )
A.(x+2)2+y2=9
B.(x-2)2+y2=9
C.(x+2)2+y2=8
D.(x-2)2+y2=8
题2.圆在x,y轴上分别截得的弦长为14和4,且圆心在直线2x+3y=0上,则此圆的方程是________.
【解题策略提醒】
求圆的方程的方法
求圆的方程主要应用待定系数法:
(1)设出圆的一般方程或标准方程,利用条件构造方程组,通过解方程组求系数.
(2)利用圆的几何性质,如弦的垂直平分线过圆心等,构造条件求系数.
题组训练二 直线与圆的位置关系
题3.若a2+b2=2c2(c≠0),则直线ax+by+c=0被圆x2+y2=1所截得的弦长为( )
A.
B.1
C.
D.
题4.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
题5.已知P为直线x+y-2=0上的点,过点P作圆O:x2+y2=1的切线,切点为M,N,若∠MPN=90°,则这样的点P有( )
A.0个
B.1个
C.2个
D.无数个
【解题策略提醒】
直线与圆的位置关系
(1)位置关系的判断:一般利用几何法判断,即判断圆心到直线的距离与半径的关系.
(2)弦长公式:直线与圆相交时,圆的弦长l,半径r,弦心距d之间满足r2=d2+.
题组训练三 圆与圆的位置关系
题6.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是________.
题7.要在一个矩形纸片上画出半径分别是4
cm和1
cm的两个外切圆,该矩形面积的最小值是( )
A.36
cm2
B.72
cm2
C.
80
cm2
D.100
cm2
题8.已知两个圆C1,C2与两坐标轴都相切,且都过点(1,-2),则C1C2=________.
【解题策略提醒】
1.关于两圆的位置关系
一般利用代数法判断两圆的位置关系,即判断圆心距与两圆半径的和差的关系,另外注意圆的位置关系与其公切线的条数是对应的,可以利用位置关系判断公切线的条数,反之亦然.
2.两圆的公共弦长
将两圆的方程作差,即可得到公共弦的方程,再利用其中一个圆,构造弦长、半径、圆心距的关系求弦长.
题组训练四 与圆有关的最值问题
题9.已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)若P(a,a+1)在圆C上,求线段PQ的长及直线PQ的斜率.
(2)求MQ的最大值和最小值.
(3)若M(m,n),求的最大值和最小值.
编号:013
课题:§2
圆与方程复习课
目标要求
1、理解并掌握圆的方程的求法.
2、理解并掌握直线与圆的位置关系.
3、理解并掌握圆与圆的位置关系.
4、理解并掌握与圆有关的最值问题.
学科素养目标
本章以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.通过本章的学习,学生将在类比直线的研究方法的基础上,进一步体会和掌握在平面直角坐标系中建立圆的方程,进而运用方程研究圆的几何性质及直线和圆、圆和圆的相互位置关系,体会数形结合的思想,逐步形成用代数方法解决几何问题的能力.
重点难点
重点:两圆相交问题;
难点:圆与圆的综合应用问题.
教学过程
思维结构简图
基础知识点
1.
圆的标准方程
(1)圆的定义:平面上到定点的距离等于定长的点的集合叫作
圆
,定点称为圆的
圆心
,定长称为圆的
半径
.
(2)标准方程:圆心为A(a,b),半径为r的圆的标准方程为
(x-a)2+(y-b)2=r2
.
(3)确定圆的标准方程的几何要素:圆心、半径.
2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
(1)在圆内:(x0-a)2+(y0-b)2
<
r2或d
<
r;
(2)在圆上:(x0-a)2+(y0-b)2
=
r2或d
=
r;
(3)在圆外:(x0-a)2+(y0-b)2
>
r2或d
>
r.
3.
方程x2+y2+Dx+Ey+F=0表示的图形
将方程左边配方,并将常数项移到右边得+=
.
(1)当D2+E2-4F>0时,表示圆心为
,半径为
的圆;
(2)当D2+E2-4F=0时,表示点
;
(3)当D2+E2-4F<0时,不表示任何图形.
【思考】
4.圆的一般方程
(1)一般方程:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0称为圆的
一般
方程.
(2)本质:圆的方程的另一种表示形式,更具有方程特征.
5.
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断:
(1)方法:
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
方法
几何法:设圆心到直线的距离d=
d<r
d=r
d>r
代数法:由消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
Δ<0
(2)本质:利用直线与圆的方程,通过定量计算研究直线与圆的位置关系.
6.(1)若两圆的半径分别为r1,r2,圆心距为d,则两圆有以下位置关系:
位置关系
公共点个数
圆心距与半径的关系
图示
两圆外离
0
d
>
r1+r2
两圆内含
d
<
|r1-r2|
两圆相交
2
|r1-r2|
<
d
<
r1+r2
两圆内切
1
d
=
|r1-r2|
两圆外切
d
=
r1+r2
(2)本质:利用圆的方程,通过定量计算研究圆与圆的位置关系.
【课堂题组训练】
题组训练一 求圆的方程
题1.已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为( )
A.(x+2)2+y2=9
B.(x-2)2+y2=9
C.(x+2)2+y2=8
D.(x-2)2+y2=8
【解析】选B.设圆C:(x-a)2+y2=r2,a>0.把点M(0,)代入得,a2+5=r2.
圆心到直线2x-y=0的距离为=,解得a=2,r=3.
所以圆C的方程为(x-2)2+y2=9.
题2.圆在x,y轴上分别截得的弦长为14和4,且圆心在直线2x+3y=0上,则此圆的方程是________.
【解析】设圆的方程为(x-a)2+(y-b)2=r2.
则解得或
圆的方程为2+2=85或2+2=85.
答案:+2=85或2+2=85
【解题策略提醒】
求圆的方程的方法
求圆的方程主要应用待定系数法:
(1)设出圆的一般方程或标准方程,利用条件构造方程组,通过解方程组求系数.
(2)利用圆的几何性质,如弦的垂直平分线过圆心等,构造条件求系数.
题组训练二 直线与圆的位置关系
题3.若a2+b2=2c2(c≠0),则直线ax+by+c=0被圆x2+y2=1所截得的弦长为( )
A.
B.1
C.
D.
【解析】选D.因为圆心(0,0)到直线ax+by+c=0的距离d===,因此根据直角三角形的关系,弦长的一半就等于=,所以弦长为.
题4.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
【解析】选C.切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为d==2,圆的半径为1,故切线长的最小值为==.
题5.已知P为直线x+y-2=0上的点,过点P作圆O:x2+y2=1的切线,切点为M,N,若∠MPN=90°,则这样的点P有( )
A.0个
B.1个
C.2个
D.无数个
【解析】选B.连接OM,ON,(图略)则OM=ON,∠MPN=∠ONP=∠OMP=90°,
所以四边形OMPN为正方形,因为圆O的半径为1,所以OP=,
因为原点(圆心)O到直线x+y-2=0的距离为,所以符合条件的点P只有一个.
【解题策略提醒】
直线与圆的位置关系
(1)位置关系的判断:一般利用几何法判断,即判断圆心到直线的距离与半径的关系.
(2)弦长公式:直线与圆相交时,圆的弦长l,半径r,弦心距d之间满足r2=d2+.
题组训练三 圆与圆的位置关系
题6.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是________.
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,圆心坐标为(a,a),半径为2.
依题意得0<<4,所以0<|a|<2.所以a∈(-2,0)∪(0,2).
答案:(-2,0)∪(0,2)
题7.要在一个矩形纸片上画出半径分别是4
cm和1
cm的两个外切圆,该矩形面积的最小值是( )
A.36
cm2
B.72
cm2
C.
80
cm2
D.100
cm2
【解析】选B.如图,作WG⊥SC,则四边形WDCG是矩形,
因为两圆相切,所以WS=SC+WD=1+4=5,
因为SG=SC-GC=4-1=3,所以WG=4,所以矩形QHBA的长AB=AD+CD+CB=1+4+4=9,
宽BH=4+4=8,所以矩形纸片面积的最小值=8×9=72
cm2.
题8.已知两个圆C1,C2与两坐标轴都相切,且都过点(1,-2),则C1C2=________.
【解析】由题意,得圆C1,C2的圆心在射线y=-x,x>0上.
设圆的方程为(x-a)2+(y+a)2=a2,a>0,
因为圆过点(1,-2),所以(1-a)2+(-2+a)2=a2,
解得a=1或a=5,即C1(1,-1),C2(5,-5),则C1C2=4.
答案:4
【解题策略提醒】
1.关于两圆的位置关系
一般利用代数法判断两圆的位置关系,即判断圆心距与两圆半径的和差的关系,另外注意圆的位置关系与其公切线的条数是对应的,可以利用位置关系判断公切线的条数,反之亦然.
2.两圆的公共弦长
将两圆的方程作差,即可得到公共弦的方程,再利用其中一个圆,构造弦长、半径、圆心距的关系求弦长.
题组训练四 与圆有关的最值问题
题9.已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)若P(a,a+1)在圆C上,求线段PQ的长及直线PQ的斜率.
(2)求MQ的最大值和最小值.
(3)若M(m,n),求的最大值和最小值.
【解析】(1)由点P(a,a+1)在圆C上,可得a2+(a+1)2-4a-14(a+1)+45=0,解得a=4,所以P(4,5).
所以PQ==2,kPQ==.
(2)圆的方程变为(x-2)2+(y-7)2=8.所以圆心C坐标为(2,7),半径r=2.可得QC==4,因此MQmax=4+2=6,MQmin=4-2=2.
(3)可知表示直线MQ的斜率,设直线MQ的方程为:
y-3=k(x+2),即kx-y+2k+3=0,则=k,由直线MQ与圆C相切时,=2,可得k=2+或k=2-,所以2-≤k≤2+,所以的最大值为2+,最小值为2-.
【解题策略提醒】
与圆有关的最值问题常见的类型
(1)求圆O上一点到圆外一点P的最大、最小距离:
dmax=OP+r,dmin=OP-r.
(2)求圆上的点到与圆相离的某条直线的最大、最小距离:设圆心到直线的距离为m,则dmax=m+r,dmin=m-r.
(3)已知某点的运动轨迹是(x-a)2+(y-b)2=r2,求,,x2+y2等式子的最值,一般运用几何法求解.
圆与方程复习课
目标要求
1、理解并掌握圆的方程的求法.
2、理解并掌握直线与圆的位置关系.
3、理解并掌握圆与圆的位置关系.
4、理解并掌握与圆有关的最值问题.
学科素养目标
本章以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.通过本章的学习,学生将在类比直线的研究方法的基础上,进一步体会和掌握在平面直角坐标系中建立圆的方程,进而运用方程研究圆的几何性质及直线和圆、圆和圆的相互位置关系,体会数形结合的思想,逐步形成用代数方法解决几何问题的能力.
重点难点
重点:两圆相交问题;
难点:圆与圆的综合应用问题.
教学过程
思维结构简图
基础知识点
1.
圆的标准方程
(1)圆的定义:平面上到定点的距离等于定长的点的集合叫作
__
,定点称为圆的
___
,定长称为圆的
_______
.
(2)标准方程:圆心为A(a,b),半径为r的圆的标准方程为
___________________
.
(3)确定圆的标准方程的几何要素:________________.
2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
(1)在圆内:(x0-a)2+(y0-b)2
_
r2或d
_
r;
(2)在圆上:(x0-a)2+(y0-b)2
_
r2或d
_
r;
(3)在圆外:(x0-a)2+(y0-b)2
r2或d
r.
3.
方程x2+y2+Dx+Ey+F=0表示的图形
将方程左边配方,并将常数项移到右边得+=
______
.
(1)当D2+E2-4F>0时,表示圆心为
_________
,半径为
________
的圆;
(2)当D2+E2-4F=0时,表示点
___________
;
(3)当D2+E2-4F<0时,不表示任何图形.
4.圆的一般方程
(1)一般方程:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0称为圆的
_____
方程.
(2)本质:圆的方程的另一种表示形式,更具有方程特征.
5.
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断:
(1)方法:
位置关系
相交
相切
相离
公共点个数
___个
1个
0个
方法
几何法:设圆心到直线的距离d=
d<r
_____
d>r
代数法:由消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
________
(2)本质:利用直线与圆的方程,通过定量计算研究直线与圆的位置关系.
6.
(1)若两圆的半径分别为r1,r2,圆心距为d,则两圆有以下位置关系:
位置关系
公共点个数
圆心距与半径的关系
图示
两圆外离
___
d
_
r1+r2
两圆内含
d
_
|r1-r2|
两圆相交
__
|r1-r2|
__
d
__
r1+r2
两圆内切
__
d
__
|r1-r2|
两圆外切
d
__
r1+r2
(2)本质:利用圆的方程,通过定量计算研究圆与圆的位置关系.
【课堂题组训练】
题组训练一 求圆的方程
题1.已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为( )
A.(x+2)2+y2=9
B.(x-2)2+y2=9
C.(x+2)2+y2=8
D.(x-2)2+y2=8
题2.圆在x,y轴上分别截得的弦长为14和4,且圆心在直线2x+3y=0上,则此圆的方程是________.
【解题策略提醒】
求圆的方程的方法
求圆的方程主要应用待定系数法:
(1)设出圆的一般方程或标准方程,利用条件构造方程组,通过解方程组求系数.
(2)利用圆的几何性质,如弦的垂直平分线过圆心等,构造条件求系数.
题组训练二 直线与圆的位置关系
题3.若a2+b2=2c2(c≠0),则直线ax+by+c=0被圆x2+y2=1所截得的弦长为( )
A.
B.1
C.
D.
题4.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
题5.已知P为直线x+y-2=0上的点,过点P作圆O:x2+y2=1的切线,切点为M,N,若∠MPN=90°,则这样的点P有( )
A.0个
B.1个
C.2个
D.无数个
【解题策略提醒】
直线与圆的位置关系
(1)位置关系的判断:一般利用几何法判断,即判断圆心到直线的距离与半径的关系.
(2)弦长公式:直线与圆相交时,圆的弦长l,半径r,弦心距d之间满足r2=d2+.
题组训练三 圆与圆的位置关系
题6.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是________.
题7.要在一个矩形纸片上画出半径分别是4
cm和1
cm的两个外切圆,该矩形面积的最小值是( )
A.36
cm2
B.72
cm2
C.
80
cm2
D.100
cm2
题8.已知两个圆C1,C2与两坐标轴都相切,且都过点(1,-2),则C1C2=________.
【解题策略提醒】
1.关于两圆的位置关系
一般利用代数法判断两圆的位置关系,即判断圆心距与两圆半径的和差的关系,另外注意圆的位置关系与其公切线的条数是对应的,可以利用位置关系判断公切线的条数,反之亦然.
2.两圆的公共弦长
将两圆的方程作差,即可得到公共弦的方程,再利用其中一个圆,构造弦长、半径、圆心距的关系求弦长.
题组训练四 与圆有关的最值问题
题9.已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)若P(a,a+1)在圆C上,求线段PQ的长及直线PQ的斜率.
(2)求MQ的最大值和最小值.
(3)若M(m,n),求的最大值和最小值.
编号:013
课题:§2
圆与方程复习课
目标要求
1、理解并掌握圆的方程的求法.
2、理解并掌握直线与圆的位置关系.
3、理解并掌握圆与圆的位置关系.
4、理解并掌握与圆有关的最值问题.
学科素养目标
本章以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.通过本章的学习,学生将在类比直线的研究方法的基础上,进一步体会和掌握在平面直角坐标系中建立圆的方程,进而运用方程研究圆的几何性质及直线和圆、圆和圆的相互位置关系,体会数形结合的思想,逐步形成用代数方法解决几何问题的能力.
重点难点
重点:两圆相交问题;
难点:圆与圆的综合应用问题.
教学过程
思维结构简图
基础知识点
1.
圆的标准方程
(1)圆的定义:平面上到定点的距离等于定长的点的集合叫作
圆
,定点称为圆的
圆心
,定长称为圆的
半径
.
(2)标准方程:圆心为A(a,b),半径为r的圆的标准方程为
(x-a)2+(y-b)2=r2
.
(3)确定圆的标准方程的几何要素:圆心、半径.
2.点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系
(1)在圆内:(x0-a)2+(y0-b)2
<
r2或d
<
r;
(2)在圆上:(x0-a)2+(y0-b)2
=
r2或d
=
r;
(3)在圆外:(x0-a)2+(y0-b)2
>
r2或d
>
r.
3.
方程x2+y2+Dx+Ey+F=0表示的图形
将方程左边配方,并将常数项移到右边得+=
.
(1)当D2+E2-4F>0时,表示圆心为
,半径为
的圆;
(2)当D2+E2-4F=0时,表示点
;
(3)当D2+E2-4F<0时,不表示任何图形.
【思考】
4.圆的一般方程
(1)一般方程:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0称为圆的
一般
方程.
(2)本质:圆的方程的另一种表示形式,更具有方程特征.
5.
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断:
(1)方法:
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
方法
几何法:设圆心到直线的距离d=
d<r
d=r
d>r
代数法:由消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
Δ<0
(2)本质:利用直线与圆的方程,通过定量计算研究直线与圆的位置关系.
6.(1)若两圆的半径分别为r1,r2,圆心距为d,则两圆有以下位置关系:
位置关系
公共点个数
圆心距与半径的关系
图示
两圆外离
0
d
>
r1+r2
两圆内含
d
<
|r1-r2|
两圆相交
2
|r1-r2|
<
d
<
r1+r2
两圆内切
1
d
=
|r1-r2|
两圆外切
d
=
r1+r2
(2)本质:利用圆的方程,通过定量计算研究圆与圆的位置关系.
【课堂题组训练】
题组训练一 求圆的方程
题1.已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为( )
A.(x+2)2+y2=9
B.(x-2)2+y2=9
C.(x+2)2+y2=8
D.(x-2)2+y2=8
【解析】选B.设圆C:(x-a)2+y2=r2,a>0.把点M(0,)代入得,a2+5=r2.
圆心到直线2x-y=0的距离为=,解得a=2,r=3.
所以圆C的方程为(x-2)2+y2=9.
题2.圆在x,y轴上分别截得的弦长为14和4,且圆心在直线2x+3y=0上,则此圆的方程是________.
【解析】设圆的方程为(x-a)2+(y-b)2=r2.
则解得或
圆的方程为2+2=85或2+2=85.
答案:+2=85或2+2=85
【解题策略提醒】
求圆的方程的方法
求圆的方程主要应用待定系数法:
(1)设出圆的一般方程或标准方程,利用条件构造方程组,通过解方程组求系数.
(2)利用圆的几何性质,如弦的垂直平分线过圆心等,构造条件求系数.
题组训练二 直线与圆的位置关系
题3.若a2+b2=2c2(c≠0),则直线ax+by+c=0被圆x2+y2=1所截得的弦长为( )
A.
B.1
C.
D.
【解析】选D.因为圆心(0,0)到直线ax+by+c=0的距离d===,因此根据直角三角形的关系,弦长的一半就等于=,所以弦长为.
题4.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
【解析】选C.切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为d==2,圆的半径为1,故切线长的最小值为==.
题5.已知P为直线x+y-2=0上的点,过点P作圆O:x2+y2=1的切线,切点为M,N,若∠MPN=90°,则这样的点P有( )
A.0个
B.1个
C.2个
D.无数个
【解析】选B.连接OM,ON,(图略)则OM=ON,∠MPN=∠ONP=∠OMP=90°,
所以四边形OMPN为正方形,因为圆O的半径为1,所以OP=,
因为原点(圆心)O到直线x+y-2=0的距离为,所以符合条件的点P只有一个.
【解题策略提醒】
直线与圆的位置关系
(1)位置关系的判断:一般利用几何法判断,即判断圆心到直线的距离与半径的关系.
(2)弦长公式:直线与圆相交时,圆的弦长l,半径r,弦心距d之间满足r2=d2+.
题组训练三 圆与圆的位置关系
题6.如果圆C:x2+y2-2ax-2ay+2a2-4=0与圆O:x2+y2=4总相交,那么实数a的取值范围是________.
【解析】圆C的标准方程为(x-a)2+(y-a)2=4,圆心坐标为(a,a),半径为2.
依题意得0<<4,所以0<|a|<2.所以a∈(-2,0)∪(0,2).
答案:(-2,0)∪(0,2)
题7.要在一个矩形纸片上画出半径分别是4
cm和1
cm的两个外切圆,该矩形面积的最小值是( )
A.36
cm2
B.72
cm2
C.
80
cm2
D.100
cm2
【解析】选B.如图,作WG⊥SC,则四边形WDCG是矩形,
因为两圆相切,所以WS=SC+WD=1+4=5,
因为SG=SC-GC=4-1=3,所以WG=4,所以矩形QHBA的长AB=AD+CD+CB=1+4+4=9,
宽BH=4+4=8,所以矩形纸片面积的最小值=8×9=72
cm2.
题8.已知两个圆C1,C2与两坐标轴都相切,且都过点(1,-2),则C1C2=________.
【解析】由题意,得圆C1,C2的圆心在射线y=-x,x>0上.
设圆的方程为(x-a)2+(y+a)2=a2,a>0,
因为圆过点(1,-2),所以(1-a)2+(-2+a)2=a2,
解得a=1或a=5,即C1(1,-1),C2(5,-5),则C1C2=4.
答案:4
【解题策略提醒】
1.关于两圆的位置关系
一般利用代数法判断两圆的位置关系,即判断圆心距与两圆半径的和差的关系,另外注意圆的位置关系与其公切线的条数是对应的,可以利用位置关系判断公切线的条数,反之亦然.
2.两圆的公共弦长
将两圆的方程作差,即可得到公共弦的方程,再利用其中一个圆,构造弦长、半径、圆心距的关系求弦长.
题组训练四 与圆有关的最值问题
题9.已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)若P(a,a+1)在圆C上,求线段PQ的长及直线PQ的斜率.
(2)求MQ的最大值和最小值.
(3)若M(m,n),求的最大值和最小值.
【解析】(1)由点P(a,a+1)在圆C上,可得a2+(a+1)2-4a-14(a+1)+45=0,解得a=4,所以P(4,5).
所以PQ==2,kPQ==.
(2)圆的方程变为(x-2)2+(y-7)2=8.所以圆心C坐标为(2,7),半径r=2.可得QC==4,因此MQmax=4+2=6,MQmin=4-2=2.
(3)可知表示直线MQ的斜率,设直线MQ的方程为:
y-3=k(x+2),即kx-y+2k+3=0,则=k,由直线MQ与圆C相切时,=2,可得k=2+或k=2-,所以2-≤k≤2+,所以的最大值为2+,最小值为2-.
【解题策略提醒】
与圆有关的最值问题常见的类型
(1)求圆O上一点到圆外一点P的最大、最小距离:
dmax=OP+r,dmin=OP-r.
(2)求圆上的点到与圆相离的某条直线的最大、最小距离:设圆心到直线的距离为m,则dmax=m+r,dmin=m-r.
(3)已知某点的运动轨迹是(x-a)2+(y-b)2=r2,求,,x2+y2等式子的最值,一般运用几何法求解.
