2021-2022学年度华东师大版七上数学第五章相交线与平行线复习课课件(34张)
文档属性
| 名称 | 2021-2022学年度华东师大版七上数学第五章相交线与平行线复习课课件(34张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 11:50:59 | ||
图片预览





文档简介
(共34张PPT)
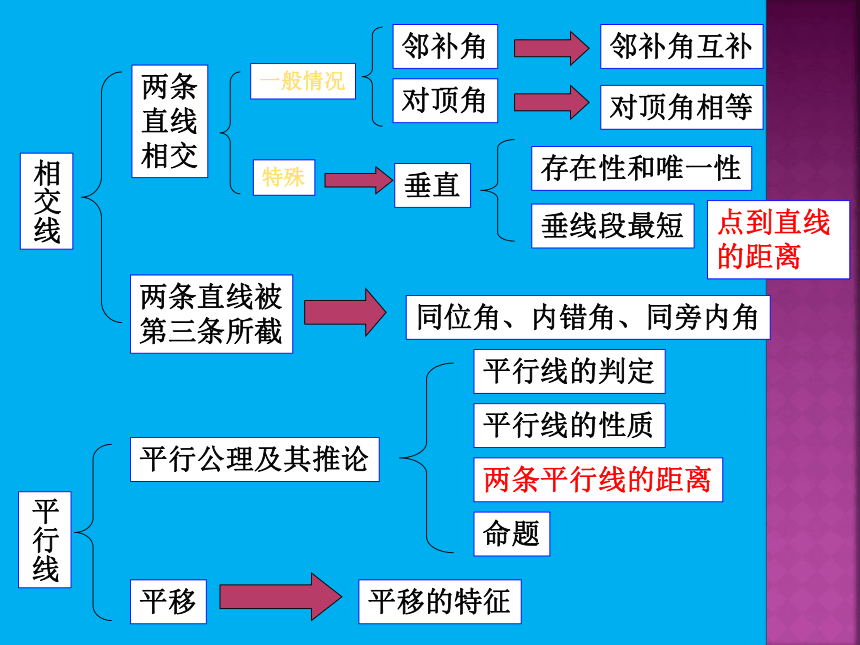
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
n条直线相交于一点,有
组对顶角。
n(n-1)
一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
两条直线平行,那么它们的同位角的角平分线也互相平行;内错角的角平分线也互相平行;同旁内角的角平分线互相垂直。
本章几个重要的结论:
1。对顶角相等
2.三线八角:同位角内错角同旁内角
3两直线相交所成的四个角中,有一个角是直角时,就称这两条直线互相垂直,交点叫做垂足
两线垂直,四个角都是直角
垂线段最短
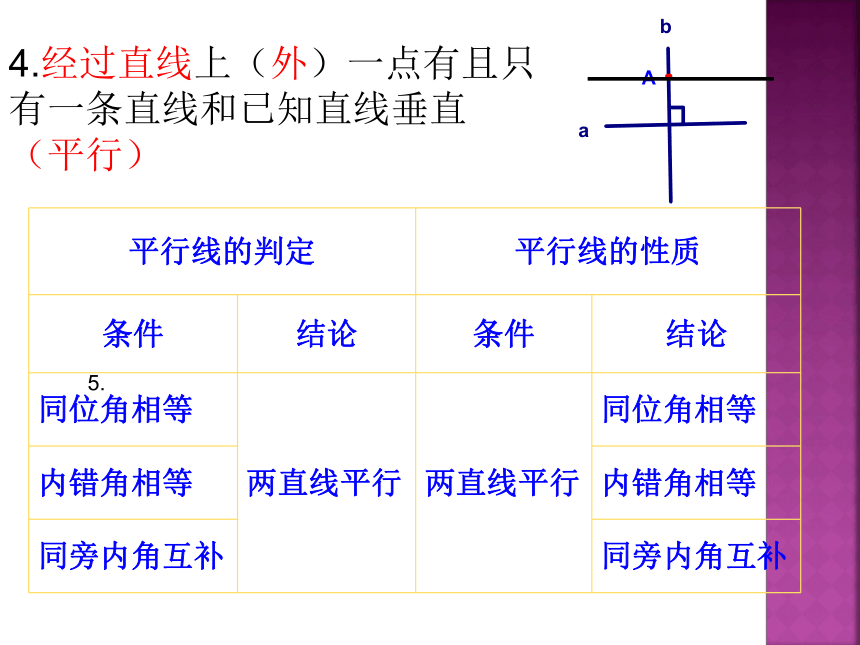
4.经过直线上(外)一点有且只有一条直线和已知直线垂直(平行)
5.
平行线的判定
平行线的性质
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
内错角相等
同旁内角互补
同旁内角互补
5.在同一个平面内,垂直于
同一条直线的两条直线平行。
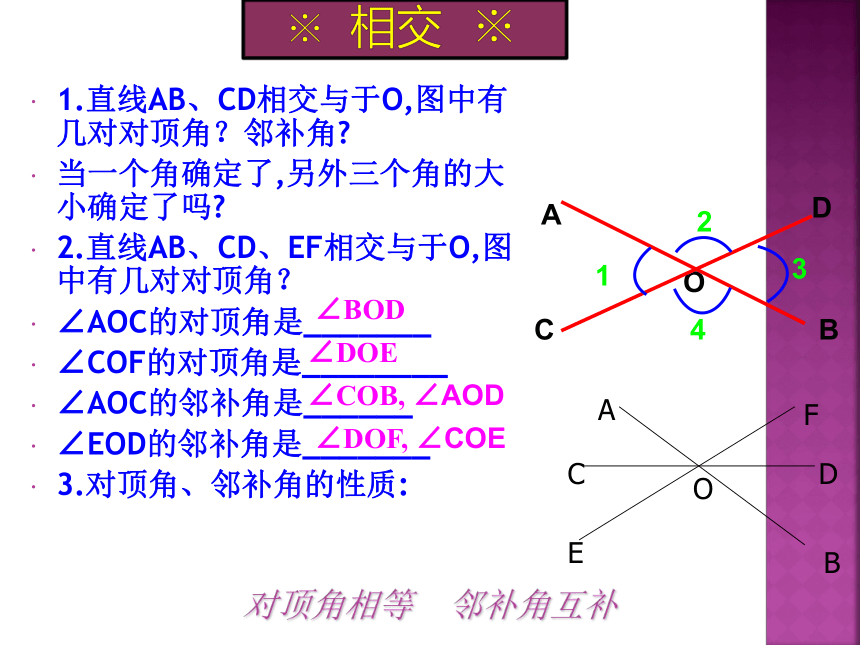
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角?
当一个角确定了,另外三个角的大小确定了吗?
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是______
∠EOD的邻补角是_______
3.对顶角、邻补角的性质:
O
A
B
C
D
1
2
3
4
A
B
C
D
E
F
O
∠BOD
∠DOE
∠COB,
∠AOD
∠DOF,
∠COE
对顶角相等
邻补角互补
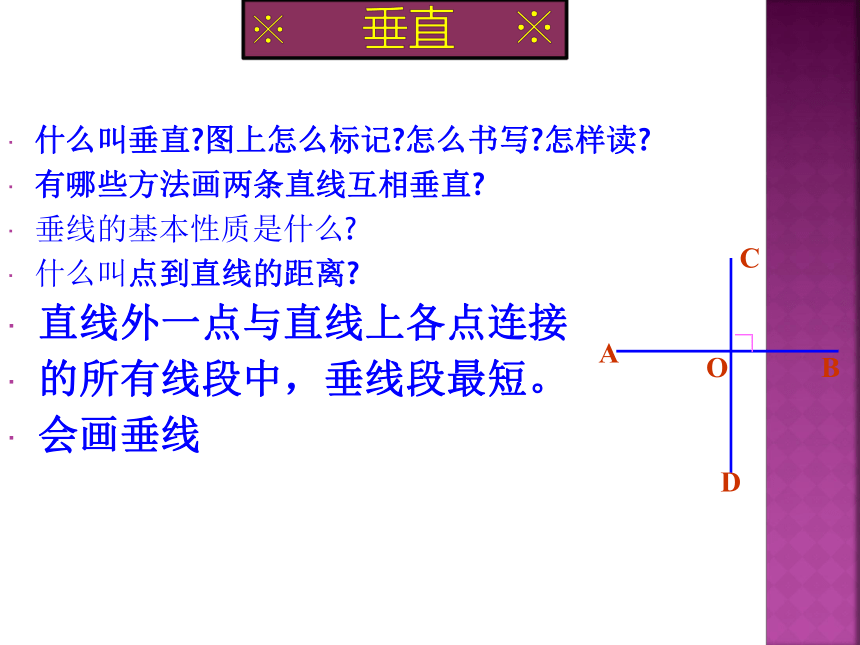
什么叫垂直?图上怎么标记?怎么书写?怎样读?
有哪些方法画两条直线互相垂直?
垂线的基本性质是什么?
什么叫点到直线的距离?
直线外一点与直线上各点连接
的所有线段中,垂线段最短。
会画垂线
A
∟
D
C
B
O
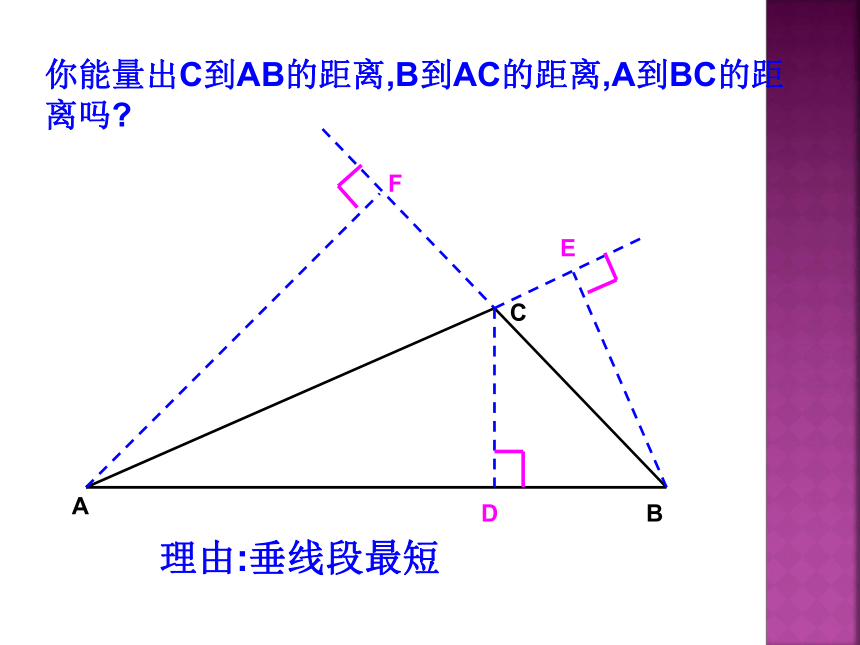
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
A
D
C
B
E
F
理由:垂线段最短
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
理由:垂线段最短
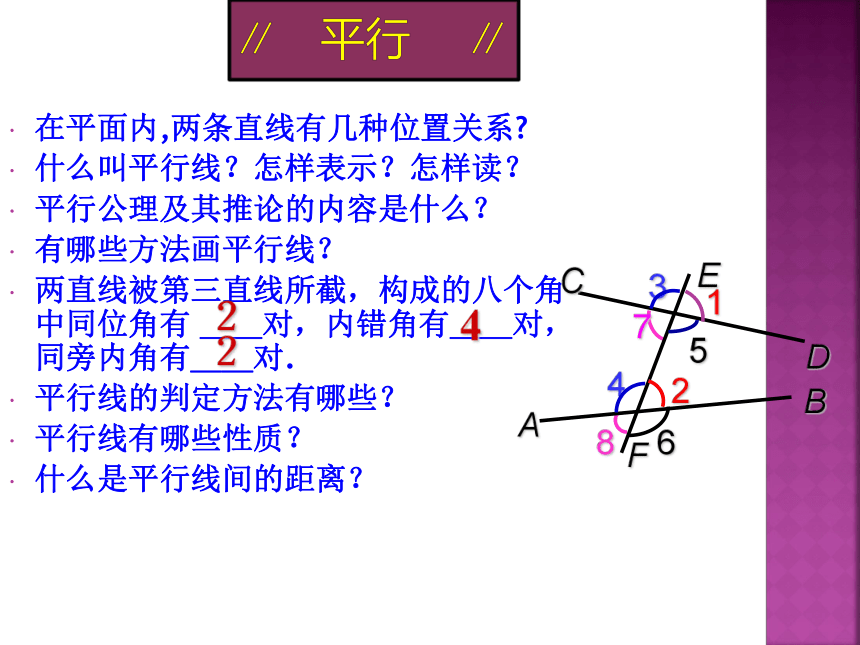
在平面内,两条直线有几种位置关系?
什么叫平行线?怎样表示?怎样读?
平行公理及其推论的内容是什么?
有哪些方法画平行线?
两直线被第三直线所截,构成的八个角中同位角有
__对,内错角有__对,同旁内角有__对.
平行线的判定方法有哪些?
平行线有哪些性质?
什么是平行线间的距离?
4
2
2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
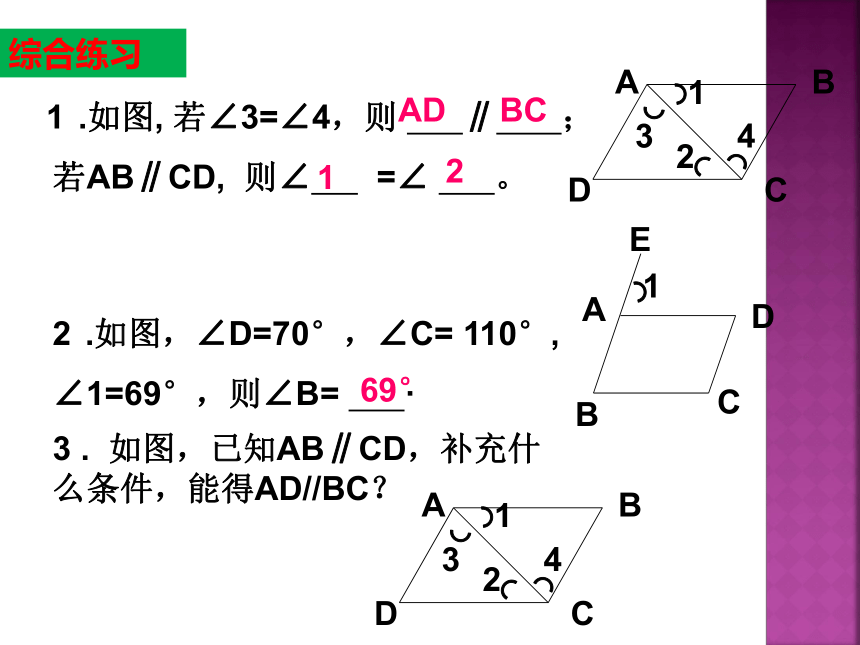
.如图,
若∠3=∠4,则
∥
;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD,
则∠
=∠
。
BC
2
.如图,∠D=70°,∠C=
110°,
∠1=69°,则∠B=
·
B
A
C
E
D
⌒
1
69°
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
3
.
如图,已知AB∥CD,补充什么条件,能得AD//BC?
综合练习
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有(
)个.
A.
2
B.
3
C.
4
D.
5
A
B
C
D
E
F
O
D
7.如图,填空
(1)∵∠B=∠1(已知)
∴____//____(
)
(2)∵CG
//
DF(已知)
∴∠2=
(
)
(3)∵∠3=∠A(已知)
∴____//____(
)
(4)∵AG
//
DF(已知)
∴∠3=_____(
)
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
(5)∵∠B+∠4=180°(已知)
∴____//____(
)
(6)∵CG
//
DF(已知)
∴∠F+
=180°(
)
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
9、如图,已知∠AEM=
∠DGN,则你能说明AB平行于CD吗?
变式1:若∠AEM=
∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
变式2:若∠AEM=
∠DGN,∠1=∠2,则图中还有平行线吗?
练习:
⒈
如图⑴,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=______°
⒉
如图⑵,若AE∥CD,
∠EBF=135°,
∠BFD=60°,∠D=
(
)
A、75°
B、45°
C、30°
D、15°
图1
图2
30°
?
135°
?
60°
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
a
d
c
b
3
1
2
2.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2
,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180
°,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
若OE⊥AB
,∠1=56°,
则∠3=_____。
E
3
O
A
B
C
D
2
1
3.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。??????
34°
60°
120
°
4.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110°
∠BOC=70°
∠AOC=20°
5.点到直线的距离是____
点到直线上一点的连线
点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
6.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=____(______________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(__________________________)
所以∠BAC+______=180°(________________)
因为∠BAC=70°
所以∠AGD=_______
命
题
定义
结构
形式
真假
能够把一个命题写成”如果…那么…’的形式
判断一件事情的语句,叫做命题
题设、结论
“如果…那么…”,
“若…则…”等
★
平行
★
1、观察右图并填空:
(1)
∠1
与
是同位角;
(2)
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行?
(1)
∠1
=
∠4;
(2)
∠2
=
∠4;
(3)
∠1
+
∠3
=
180?;
a
b
l
m
n
1
2
3
4
基础练习:
a
∥
b
l∥m
l∥
n
3.如图:∠
1=100°∠2=80°,
∠3=105°
则∠4=_______
a
b
c
d
1
2
3
4
4.
两条直线被第三条直线所截,则(
)
A
同位角相等
B
同旁内角互补
C
内错角相等
D
以上都不对
基础练习:
105°
D
5.如图,
若∠3=∠4,则
∥
;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD,
则∠
=∠
。
BC
2
6.如图,∠D=70°,∠C=
110°,∠1=69°,
则∠B=
·
B
A
C
E
D
⌒
1
69°
基础练习:
如图,直线EF过点A,
D是BA延长线上的点
,具备什么条件时,可以判定EF
BC
?
为什么
?
B
C
E
F
D
A
一题多解:
例1。
已知∠DAC=
∠ACB,
∠D+∠DFE=1800,求证:EF//BC
证明:
因为
∠DAC=
∠ACB
(已知)
所以
AD//
BC
(内错角相等,两直线平行)
因为
∠D+∠DFE=1800(已知)
所以AD//
EF
(同旁内角互补,两直线平行)
因为
EF//
BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例题精讲:
例2
:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG
=∠C
。
例题连讲:
证明:
因为由AC∥DE
(已知)
所以∠ACD=
∠2
(两直线平行,内错角相等)
因为∠1=∠2(已知)
所以
∠1=∠ACD(等量代换)
所以AB
∥
CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例题连讲:
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD.
已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系
F
1
2
1
2
F
A
B
C
D
E
创新探究:
如图给出下列论断:
(1)AB//CD
(2)AD//BC
(3)∠A=∠C
以上,其中两个作为题设,另一个作为结论,用
“如果……,
那么……”的形式,写出一个你认为正确的命题。
A
B
C
D
分析:
不妨选择(1)与(2)作条件,由平
行性质
“两直线平行,同旁内角互补”
可得∠A=∠C,故满足要求。由(1)与
(3)也能得出(2)成立,由(2)与(3)也
能得出(1)成立。
解:
如果在四边形ABCD中,AB//DC、AD//BC,那么∠A=∠C。
创新探究:
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
n条直线相交于一点,有
组对顶角。
n(n-1)
一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
两条直线平行,那么它们的同位角的角平分线也互相平行;内错角的角平分线也互相平行;同旁内角的角平分线互相垂直。
本章几个重要的结论:
1。对顶角相等
2.三线八角:同位角内错角同旁内角
3两直线相交所成的四个角中,有一个角是直角时,就称这两条直线互相垂直,交点叫做垂足
两线垂直,四个角都是直角
垂线段最短
4.经过直线上(外)一点有且只有一条直线和已知直线垂直(平行)
5.
平行线的判定
平行线的性质
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
内错角相等
同旁内角互补
同旁内角互补
5.在同一个平面内,垂直于
同一条直线的两条直线平行。
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角?
当一个角确定了,另外三个角的大小确定了吗?
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是______
∠EOD的邻补角是_______
3.对顶角、邻补角的性质:
O
A
B
C
D
1
2
3
4
A
B
C
D
E
F
O
∠BOD
∠DOE
∠COB,
∠AOD
∠DOF,
∠COE
对顶角相等
邻补角互补
什么叫垂直?图上怎么标记?怎么书写?怎样读?
有哪些方法画两条直线互相垂直?
垂线的基本性质是什么?
什么叫点到直线的距离?
直线外一点与直线上各点连接
的所有线段中,垂线段最短。
会画垂线
A
∟
D
C
B
O
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
A
D
C
B
E
F
理由:垂线段最短
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
理由:垂线段最短
在平面内,两条直线有几种位置关系?
什么叫平行线?怎样表示?怎样读?
平行公理及其推论的内容是什么?
有哪些方法画平行线?
两直线被第三直线所截,构成的八个角中同位角有
__对,内错角有__对,同旁内角有__对.
平行线的判定方法有哪些?
平行线有哪些性质?
什么是平行线间的距离?
4
2
2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
.如图,
若∠3=∠4,则
∥
;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD,
则∠
=∠
。
BC
2
.如图,∠D=70°,∠C=
110°,
∠1=69°,则∠B=
·
B
A
C
E
D
⌒
1
69°
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
3
.
如图,已知AB∥CD,补充什么条件,能得AD//BC?
综合练习
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有(
)个.
A.
2
B.
3
C.
4
D.
5
A
B
C
D
E
F
O
D
7.如图,填空
(1)∵∠B=∠1(已知)
∴____//____(
)
(2)∵CG
//
DF(已知)
∴∠2=
(
)
(3)∵∠3=∠A(已知)
∴____//____(
)
(4)∵AG
//
DF(已知)
∴∠3=_____(
)
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
(5)∵∠B+∠4=180°(已知)
∴____//____(
)
(6)∵CG
//
DF(已知)
∴∠F+
=180°(
)
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
9、如图,已知∠AEM=
∠DGN,则你能说明AB平行于CD吗?
变式1:若∠AEM=
∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
变式2:若∠AEM=
∠DGN,∠1=∠2,则图中还有平行线吗?
练习:
⒈
如图⑴,已知
AB∥CD,
∠1=30°,
∠2=90°,则∠3=______°
⒉
如图⑵,若AE∥CD,
∠EBF=135°,
∠BFD=60°,∠D=
(
)
A、75°
B、45°
C、30°
D、15°
图1
图2
30°
?
135°
?
60°
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
a
d
c
b
3
1
2
2.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2
,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180
°,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
若OE⊥AB
,∠1=56°,
则∠3=_____。
E
3
O
A
B
C
D
2
1
3.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。??????
34°
60°
120
°
4.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110°
∠BOC=70°
∠AOC=20°
5.点到直线的距离是____
点到直线上一点的连线
点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
6.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=____(______________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(__________________________)
所以∠BAC+______=180°(________________)
因为∠BAC=70°
所以∠AGD=_______
命
题
定义
结构
形式
真假
能够把一个命题写成”如果…那么…’的形式
判断一件事情的语句,叫做命题
题设、结论
“如果…那么…”,
“若…则…”等
★
平行
★
1、观察右图并填空:
(1)
∠1
与
是同位角;
(2)
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行?
(1)
∠1
=
∠4;
(2)
∠2
=
∠4;
(3)
∠1
+
∠3
=
180?;
a
b
l
m
n
1
2
3
4
基础练习:
a
∥
b
l∥m
l∥
n
3.如图:∠
1=100°∠2=80°,
∠3=105°
则∠4=_______
a
b
c
d
1
2
3
4
4.
两条直线被第三条直线所截,则(
)
A
同位角相等
B
同旁内角互补
C
内错角相等
D
以上都不对
基础练习:
105°
D
5.如图,
若∠3=∠4,则
∥
;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD,
则∠
=∠
。
BC
2
6.如图,∠D=70°,∠C=
110°,∠1=69°,
则∠B=
·
B
A
C
E
D
⌒
1
69°
基础练习:
如图,直线EF过点A,
D是BA延长线上的点
,具备什么条件时,可以判定EF
BC
?
为什么
?
B
C
E
F
D
A
一题多解:
例1。
已知∠DAC=
∠ACB,
∠D+∠DFE=1800,求证:EF//BC
证明:
因为
∠DAC=
∠ACB
(已知)
所以
AD//
BC
(内错角相等,两直线平行)
因为
∠D+∠DFE=1800(已知)
所以AD//
EF
(同旁内角互补,两直线平行)
因为
EF//
BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例题精讲:
例2
:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG
=∠C
。
例题连讲:
证明:
因为由AC∥DE
(已知)
所以∠ACD=
∠2
(两直线平行,内错角相等)
因为∠1=∠2(已知)
所以
∠1=∠ACD(等量代换)
所以AB
∥
CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例题连讲:
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD.
已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系
F
1
2
1
2
F
A
B
C
D
E
创新探究:
如图给出下列论断:
(1)AB//CD
(2)AD//BC
(3)∠A=∠C
以上,其中两个作为题设,另一个作为结论,用
“如果……,
那么……”的形式,写出一个你认为正确的命题。
A
B
C
D
分析:
不妨选择(1)与(2)作条件,由平
行性质
“两直线平行,同旁内角互补”
可得∠A=∠C,故满足要求。由(1)与
(3)也能得出(2)成立,由(2)与(3)也
能得出(1)成立。
解:
如果在四边形ABCD中,AB//DC、AD//BC,那么∠A=∠C。
创新探究:
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
