第二章 一元二次方程单元训练卷(Word版含解析)-2021-2022学年度北师大版九年级数学上册
文档属性
| 名称 | 第二章 一元二次方程单元训练卷(Word版含解析)-2021-2022学年度北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 42.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览




文档简介
第二章
一元二次方程单元训练卷-2021-2022学年度北师大版九年级数学上册
一、选择题
1.一元二次方程
的二次项系数是(??
)
A.1
B.2
C.-2
D.3
2.关于x的一元二次方程
x2+ax-4=0
一个根是1,则a的值是(??
)
A.0
B.1
C.3
D.-3
3.用配方法将
变形,结果是(??
)
A.
B.
C.
D.
4.若关于x的一元二次方程
有两个不相等的实数根,则k的取值范围是(??
)
A.
B.
C.
且
D.
5.下列方程中有两个相等实数根的是(??
)
A.
B.
C.
D.
6.若x1、x2是方程x2-2x-3=0的两根,则x1+x2+x1x2的值是(??????
)
A.1
B.-1
C.5
D.-5
7.参加一次绿色有机农产品交易会的每两家公司都签订了一份合同,所有公司共签订了45份合同,参加这次交易会的公司共有(?
)
A.9家
B.10家
C.10家或9家
D.19家
8.定义:当关于
的一元二次方程
满足
时,称此方程为“合理”方程.若“合理”方程
有两个相等的实数根,则下列等式正确的是(??
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
9.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加
株花苗,下面列出的方程中符合题意的是(?
)
A.?
B.?
C.?
D.?
10.若m、n是一元二次方程x2+3x﹣9=0的两个根,则
的值是(??
)
A.?4???????????????????????????????B.?5???????????????????????????????C.?6???????????????????????????D.?12
二、填空题
11..一元二次方程x2﹣3x=0的解是
???1???.
12..关于x的一元二次方程x2﹣5x+m=0有两个相等的实数根,则m=???1???.
13.已知关于x的一元二次方程mx2+3x+m2﹣2m=0有一个根为0,则m=________.
14.若m是方程
的一个根,则
的值为________.
15.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即
尺,秋千踏板离地的距离
就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
16.若一元二次方程
有一根为
,则
________.
三、解答题
17.解方程:
(1)
;
(2)
.
18.解方程:x(x﹣5)=5﹣x
.
小滨的解答如下:
解:原方程可化简为x(x﹣5)=﹣(x﹣5),
方程两边同时除以x﹣5,得x=﹣1,
小滨的解答是否正确,如不正确,写出正确的解答过程.
19.若x1
,
x2是关于x的一元二次方程ax2+bx+c=0的两个根,则x1+x2=﹣
,x1?x2=
.现已知一元二次方程px2+2x+q=0的两根分别为m,n.
(1)若m=2,n=﹣4,求p,q的值;
(2)若p=3,q=﹣1,求m+mn+n的值.
20.已知关于
的一元二次方程
有实数根.
(1)求
的取值范围;
(2)若该方程的两个实数根分别为
、
,且
,求
的值.
21.为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2019年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2021年底三年累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2021年底共建设了多少万平方米的廉租房?
22.为了丰富市民的文化生活,我市某景点开放夜游项目.为吸引游客组团来此夜游,特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格为60元/人;
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于50元/人.
(1)当夜游人数为15人时,人均门票价格为________元;当夜游人数为25人时,人均门票价格为________元;
(2)若某单位支付门票费用共1232元,则该单位这次共有多少名员工去此景点夜游?
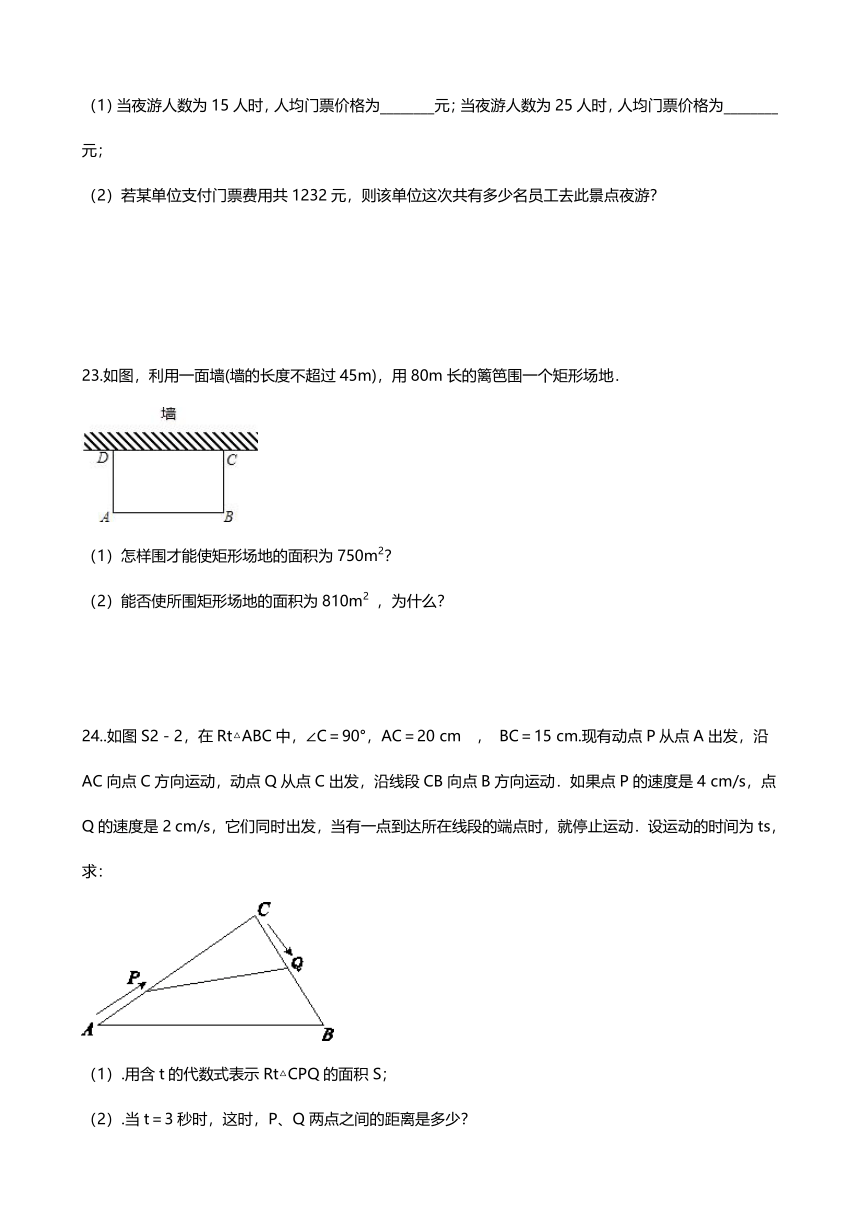
23.如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2????
(2)能否使所围矩形场地的面积为810m2
,为什么????
24..如图S2-2,在Rt△ABC中,∠C=90°,AC=20
cm
,
BC=15
cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是4
cm/s,点Q的速度是2
cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动的时间为ts,求:
(1).用含t的代数式表示Rt△CPQ的面积S;
(2).当t=3秒时,这时,P、Q两点之间的距离是多少?
(3).当t为多少秒时,S=S△ABC?
答案
一、选择题
1.解:由一元二次方程
可得二次项系数为1;
故答案为:A.
2.解:把
代入
可得:
,解得:
;
故答案为:C.
3.解:二次项系数化1得
,
加一次项系数一半的平方得
,
整理得
.
故答案为:C.
4.解:由关于x的一元二次方程
有两个不相等的实数根,可得:
,
解得:
;
故答案为:D.
5.解:A、(x-1)2=0中x1=x2=1,故符合题意;
B、(x-1)(x+1)=0中x1=1,x2=-1,故不符合题意;
C、(x-1)2=4中x1=3,x2=-1,故不符合题意;
D、x(x-1)=0中x1=0,x2=1,故不符合题意;
故答案为:A.
6.解:∵x1、x2是方程x2-2x-3=0的两个根
∴x1+x2=-
=2,x1x2=
=-3
∴x1+x2+2x1x2=2-3=-1.
故答案为:B.
7.解:设有x家公司参加,依题意可得,
,
整理得:
,
解得:
.
答:共有10家公司参加商品交易会.
故答案为:B.
8.解:∵“合理”方程有两个相等的实数根
∴
4m-2n+p=0
①
=n2-4mp=0
②
则有
p=2n-4m代入②得:
n2-4m
(2n-4m)
=0
16m2-8mn=-
n2
16m2-8mn+n2=-n2+n2
∴(4m-n)2=0
∴4m=n,代入①得
n-2n+p=0
∴n=p
∴
4m=n=p
故答案为:D
9.解:设每盆应该多植x株,由题意得
,
故答案为:A.
10.解:∵m、n是一元二次方程x2+3x?9=0的两个根,
∴m+n=?3,mn=?9,
∵m是x2+3x?9=0的一个根,
∴m2+3m?9=0,
∴m2+3m=9,
∴m2+4m+n=m2+3m+m+n=9+(m+n)=9?3=6.
故答案为:C.
二、填空题
11.解:x2﹣3x=0,
x(x﹣3)=0,
∴x1=0,x2=3.
故答案为:x1=0,x2=3.
12.解:∵关于x的一元二次方程x2﹣5x+m=0有两个相等的实数根,
∴Δ=b2﹣4ac=25﹣4m=0,
解得:m=
.
故答案为:
.
13.解:将x=0代入得:m2-2m=0,
解得:m1=0,m2=2.
∵方程为一元二次方程,
∴m≠0.
故答案为:2.
14.解:∵m是方程
的一个根,
∴
,即
,
∴
;
故答案为1.
15.解:设秋千的绳索长为x尺,
由题意知:OC=x-(5-1)=(x-4)尺,CP′=10尺,OP′=x尺,
在Rt△OCP′中,由勾股定理得:
(x-4)?+10?=x?,
解得:x=14.5,
故答案为:14.5.
16.∵一元二次方程
,有一根为
,
∴
,
∴
.
故答案为:2021.
三、解答题
17.
(1)解:
,即
∴a=1,b=4,c=-1,△=b2-4ac=16+4=20,
∴
,
∴
,
.
(2)解:
分解因式得:
可得
或
∴
,
18.
解:不正确.
正确的解答过程如下:x
(x-5)=-(x-5),
x
(x-5)+(x-5)=0,
(x-5)
(x+1)=0,
则x-5=0或x+1=0.
解得x=5,x=-1.
19.
(1)解:根据题意得2﹣4=﹣
,2×(﹣4)=
,
所以p=1,q=﹣8
(2)解:根据m+n=﹣
=﹣
,mn=﹣
,
所以m+mn+n=m+n+mn=﹣
﹣
=﹣1.
20.(1)解:由题意可得:
解得:
即实数m的取值范围是
(2)解:由
可得:
∵
;
∴
解得:
或
∵
∴
即
的值为-2
21.(1)解:设市政府投资的年平均增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
整理,得:x2+3x
1.75=0,
解得x1=0.5,x2=
3.5(舍去),
答:每年市政府投资的增长率为50%
(2)解:到2021年底共建廉租房面积=9.5÷
=38(万平方米).
22.
(1)60;50
(2)解:假设共有x名员工去此景点夜游
∵
,
则
,
①
,
∴
,
解得
.
②
,
,
解得
,不为整数,舍去.
∴综上所述,共有22名员工去夜游.
(1)由标准一得,当夜游人数为15人时,人均门票价格为60元;
由标准二得60-(25-20)×2=50(元),
故答案为:60,50.
23.
(1)解:设所围矩形ABCD的长AB为x米,则宽AD为
米.
依题意,得
,即
.
解此方程,得x1=30,x2=50.
∵墙的长度不超过45m,∴x2=50不合题意,应舍去.
当x=30时,
.
答:当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2
.
(2)解:不能.理由如下:
由
得
.
∵
,
∴方程
没有实数根.
∴不能使所围矩形场地的面积为810m2
.
24.
(1)解:S=20t-4t2
(2)解:当t=3时,CP=20-4×3=8(cm),CQ=2×3=6(cm),∴PQ=10(cm)
(3)解:列方程20t-4t2=××15×20,解得t=2或t=3.
∴t为2秒或3秒时S=S△ABC.
一元二次方程单元训练卷-2021-2022学年度北师大版九年级数学上册
一、选择题
1.一元二次方程
的二次项系数是(??
)
A.1
B.2
C.-2
D.3
2.关于x的一元二次方程
x2+ax-4=0
一个根是1,则a的值是(??
)
A.0
B.1
C.3
D.-3
3.用配方法将
变形,结果是(??
)
A.
B.
C.
D.
4.若关于x的一元二次方程
有两个不相等的实数根,则k的取值范围是(??
)
A.
B.
C.
且
D.
5.下列方程中有两个相等实数根的是(??
)
A.
B.
C.
D.
6.若x1、x2是方程x2-2x-3=0的两根,则x1+x2+x1x2的值是(??????
)
A.1
B.-1
C.5
D.-5
7.参加一次绿色有机农产品交易会的每两家公司都签订了一份合同,所有公司共签订了45份合同,参加这次交易会的公司共有(?
)
A.9家
B.10家
C.10家或9家
D.19家
8.定义:当关于
的一元二次方程
满足
时,称此方程为“合理”方程.若“合理”方程
有两个相等的实数根,则下列等式正确的是(??
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
9.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加
株花苗,下面列出的方程中符合题意的是(?
)
A.?
B.?
C.?
D.?
10.若m、n是一元二次方程x2+3x﹣9=0的两个根,则
的值是(??
)
A.?4???????????????????????????????B.?5???????????????????????????????C.?6???????????????????????????D.?12
二、填空题
11..一元二次方程x2﹣3x=0的解是
???1???.
12..关于x的一元二次方程x2﹣5x+m=0有两个相等的实数根,则m=???1???.
13.已知关于x的一元二次方程mx2+3x+m2﹣2m=0有一个根为0,则m=________.
14.若m是方程
的一个根,则
的值为________.
15.我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即
尺,秋千踏板离地的距离
就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为________尺.
16.若一元二次方程
有一根为
,则
________.
三、解答题
17.解方程:
(1)
;
(2)
.
18.解方程:x(x﹣5)=5﹣x
.
小滨的解答如下:
解:原方程可化简为x(x﹣5)=﹣(x﹣5),
方程两边同时除以x﹣5,得x=﹣1,
小滨的解答是否正确,如不正确,写出正确的解答过程.
19.若x1
,
x2是关于x的一元二次方程ax2+bx+c=0的两个根,则x1+x2=﹣
,x1?x2=
.现已知一元二次方程px2+2x+q=0的两根分别为m,n.
(1)若m=2,n=﹣4,求p,q的值;
(2)若p=3,q=﹣1,求m+mn+n的值.
20.已知关于
的一元二次方程
有实数根.
(1)求
的取值范围;
(2)若该方程的两个实数根分别为
、
,且
,求
的值.
21.为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2019年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2021年底三年累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2021年底共建设了多少万平方米的廉租房?
22.为了丰富市民的文化生活,我市某景点开放夜游项目.为吸引游客组团来此夜游,特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格为60元/人;
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于50元/人.
(1)当夜游人数为15人时,人均门票价格为________元;当夜游人数为25人时,人均门票价格为________元;
(2)若某单位支付门票费用共1232元,则该单位这次共有多少名员工去此景点夜游?
23.如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2????
(2)能否使所围矩形场地的面积为810m2
,为什么????
24..如图S2-2,在Rt△ABC中,∠C=90°,AC=20
cm
,
BC=15
cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是4
cm/s,点Q的速度是2
cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动的时间为ts,求:
(1).用含t的代数式表示Rt△CPQ的面积S;
(2).当t=3秒时,这时,P、Q两点之间的距离是多少?
(3).当t为多少秒时,S=S△ABC?
答案
一、选择题
1.解:由一元二次方程
可得二次项系数为1;
故答案为:A.
2.解:把
代入
可得:
,解得:
;
故答案为:C.
3.解:二次项系数化1得
,
加一次项系数一半的平方得
,
整理得
.
故答案为:C.
4.解:由关于x的一元二次方程
有两个不相等的实数根,可得:
,
解得:
;
故答案为:D.
5.解:A、(x-1)2=0中x1=x2=1,故符合题意;
B、(x-1)(x+1)=0中x1=1,x2=-1,故不符合题意;
C、(x-1)2=4中x1=3,x2=-1,故不符合题意;
D、x(x-1)=0中x1=0,x2=1,故不符合题意;
故答案为:A.
6.解:∵x1、x2是方程x2-2x-3=0的两个根
∴x1+x2=-
=2,x1x2=
=-3
∴x1+x2+2x1x2=2-3=-1.
故答案为:B.
7.解:设有x家公司参加,依题意可得,
,
整理得:
,
解得:
.
答:共有10家公司参加商品交易会.
故答案为:B.
8.解:∵“合理”方程有两个相等的实数根
∴
4m-2n+p=0
①
=n2-4mp=0
②
则有
p=2n-4m代入②得:
n2-4m
(2n-4m)
=0
16m2-8mn=-
n2
16m2-8mn+n2=-n2+n2
∴(4m-n)2=0
∴4m=n,代入①得
n-2n+p=0
∴n=p
∴
4m=n=p
故答案为:D
9.解:设每盆应该多植x株,由题意得
,
故答案为:A.
10.解:∵m、n是一元二次方程x2+3x?9=0的两个根,
∴m+n=?3,mn=?9,
∵m是x2+3x?9=0的一个根,
∴m2+3m?9=0,
∴m2+3m=9,
∴m2+4m+n=m2+3m+m+n=9+(m+n)=9?3=6.
故答案为:C.
二、填空题
11.解:x2﹣3x=0,
x(x﹣3)=0,
∴x1=0,x2=3.
故答案为:x1=0,x2=3.
12.解:∵关于x的一元二次方程x2﹣5x+m=0有两个相等的实数根,
∴Δ=b2﹣4ac=25﹣4m=0,
解得:m=
.
故答案为:
.
13.解:将x=0代入得:m2-2m=0,
解得:m1=0,m2=2.
∵方程为一元二次方程,
∴m≠0.
故答案为:2.
14.解:∵m是方程
的一个根,
∴
,即
,
∴
;
故答案为1.
15.解:设秋千的绳索长为x尺,
由题意知:OC=x-(5-1)=(x-4)尺,CP′=10尺,OP′=x尺,
在Rt△OCP′中,由勾股定理得:
(x-4)?+10?=x?,
解得:x=14.5,
故答案为:14.5.
16.∵一元二次方程
,有一根为
,
∴
,
∴
.
故答案为:2021.
三、解答题
17.
(1)解:
,即
∴a=1,b=4,c=-1,△=b2-4ac=16+4=20,
∴
,
∴
,
.
(2)解:
分解因式得:
可得
或
∴
,
18.
解:不正确.
正确的解答过程如下:x
(x-5)=-(x-5),
x
(x-5)+(x-5)=0,
(x-5)
(x+1)=0,
则x-5=0或x+1=0.
解得x=5,x=-1.
19.
(1)解:根据题意得2﹣4=﹣
,2×(﹣4)=
,
所以p=1,q=﹣8
(2)解:根据m+n=﹣
=﹣
,mn=﹣
,
所以m+mn+n=m+n+mn=﹣
﹣
=﹣1.
20.(1)解:由题意可得:
解得:
即实数m的取值范围是
(2)解:由
可得:
∵
;
∴
解得:
或
∵
∴
即
的值为-2
21.(1)解:设市政府投资的年平均增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
整理,得:x2+3x
1.75=0,
解得x1=0.5,x2=
3.5(舍去),
答:每年市政府投资的增长率为50%
(2)解:到2021年底共建廉租房面积=9.5÷
=38(万平方米).
22.
(1)60;50
(2)解:假设共有x名员工去此景点夜游
∵
,
则
,
①
,
∴
,
解得
.
②
,
,
解得
,不为整数,舍去.
∴综上所述,共有22名员工去夜游.
(1)由标准一得,当夜游人数为15人时,人均门票价格为60元;
由标准二得60-(25-20)×2=50(元),
故答案为:60,50.
23.
(1)解:设所围矩形ABCD的长AB为x米,则宽AD为
米.
依题意,得
,即
.
解此方程,得x1=30,x2=50.
∵墙的长度不超过45m,∴x2=50不合题意,应舍去.
当x=30时,
.
答:当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2
.
(2)解:不能.理由如下:
由
得
.
∵
,
∴方程
没有实数根.
∴不能使所围矩形场地的面积为810m2
.
24.
(1)解:S=20t-4t2
(2)解:当t=3时,CP=20-4×3=8(cm),CQ=2×3=6(cm),∴PQ=10(cm)
(3)解:列方程20t-4t2=××15×20,解得t=2或t=3.
∴t为2秒或3秒时S=S△ABC.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
