3.3幂函数课件-2021--2022学年高一上学期数学人教A版必修一(共18张PPT)
文档属性
| 名称 | 3.3幂函数课件-2021--2022学年高一上学期数学人教A版必修一(共18张PPT) | 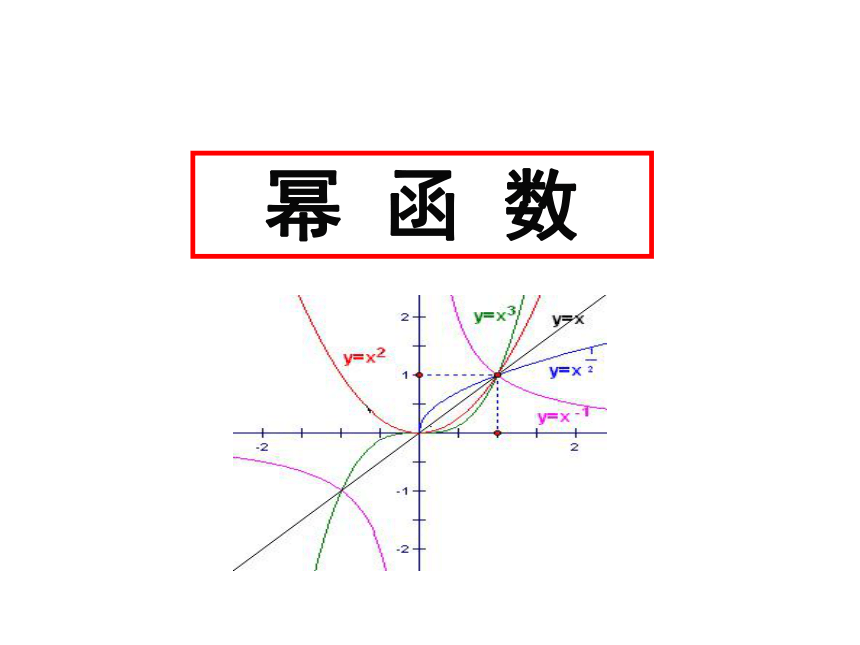 | |
| 格式 | ppt | ||
| 文件大小 | 544.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:57:12 | ||
图片预览






文档简介
(共18张PPT)
幂
函
数
问题引入:
1、如果张红购买了每千克1元的蔬菜x千克,
则所需的钱数
=____元.
2、如果正方形的边长为x,则面积
=_____.
3、如果正方体的边长为x,体积为y,
那么
=
4、如果一个正方形场地的面积为x,边长为y那么
=______.
5、如果某人x
秒内骑车行进了1公里,骑车的速度为y公里/秒,那么
=______
以上问题中的函数具有什么共同特征?
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。
新课
一、幂函数的概念
探究1:你能举几个学过的幂函数的例子吗?
一般地,函数
叫做幂函数,其中
是自变量,
是常数。
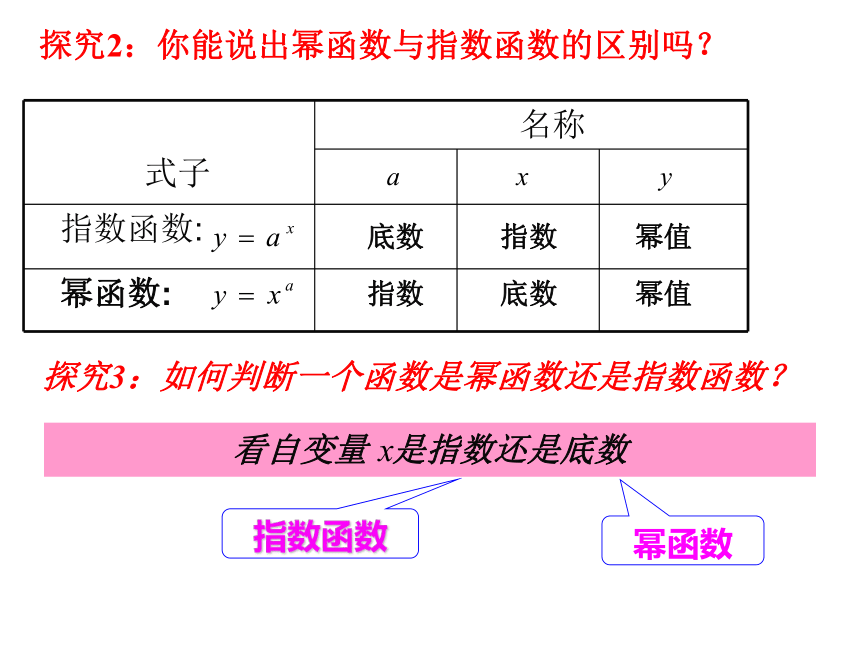
式子
名称
指数函数:
幂函数:
底数
指数
指数
底数
幂值
幂值
探究3:如何判断一个函数是幂函数还是指数函数?
幂函数
指数函数
探究2:你能说出幂函数与指数函数的区别吗?
看自变量
是指数还是底数
1、下面几个函数中,哪几个函数是幂函数?
答案(1)(4)(6)
练习
二、幂函数性质的探究:
探究4:结合前面指数函数与对数函数的方法,我们应如何研究幂函数呢?
作具体幂函数的图象→观察图象特征→总结函数性质
探究5:在同一坐标系中作出幂函数
的图象。
对于幂函数,我们只讨论
=1,2,3,
,–1
时的情形。
对于幂函数,我们只讨论
=1,2,3,
,–1
时的情形。
二.幂函数的图象及性质
探究6:
(探究性质)请同学们结合幂函数图象,将你发现的结论填在下面的表格内:
定义域
值
域
单调性
公共点
R
R
R
[0,+∞)
{x|
x
≠
0}
R
[0,+∞)
R
[0,+∞)
{y|
y≠
0}
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
R上是
增函数
在(-∞,0]上是减函数,在[0,
+∞)上是增函数
R上是增函数
在[0,+∞)上是增函数
在(
-∞,0)和(0,
+∞)上是减函数
(1,1)
奇偶性
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1);
三、幂函数的性质
(3)一般地,幂函数的图象在直线
的右侧,指数大的在上,指数小的在下,在
轴与直线
之间正好相反;
幂函数在第一象限内的性质
(1)-(3)
(2)如果
,则幂函数的图像都过
和
,并且在区间
上是增函数;
如果
,则幂函数的图像在区间
上是减函数,在第一
象限内,图像向上无限地逼近
轴,向右无限地逼近
轴;
如果
,则幂函数
是一条不包含(0,1)的直线
(4)幂函数图像不过第四象限。
(5)幂函数的奇偶性:
是奇函数;
是偶函数;
是非奇非偶函数。
例1:
已知幂函数的图象过点
,试求出此函数的解析式.
解:设
由题意得
总结:
(1)
理解并掌握形如
的形式就是幂函数的定义
(2)
充分理解并掌握幂函数的性质和特征
四、例题讲解
例2、下列结论中,正确的是(
)
C
A幂函数的图像都通过点(0,0),(1,1)
B幂函数的图像可以出现在第四象限
C当幂指数
取
时,幂函数
是增函数
D当幂指数
时,幂函数
在定义域上是减函数
例3、已知幂函数
的图象过点
,则
的
值(
)
A
A
B
C
D
A
B
C
D
例4、如果幂函数
的图像不过原
点,则m的取值是(
)
B
A
B
C
D
五、小
结
(1)
幂函数的定义;
(2)
5个具体幂函数的图像及性质;
(3)
幂函数的5条性质;
(4)
掌握幂函数中指数的变化对图像影响。
思考题:根据幂函数的性质画出以下函数的图像
六、作
业
1、必做:课本79页习题2.3;《优化设计》2.3幂函数95页至97页;
2、选做:《优化设计》98页能力提升第8题。
幂
函
数
问题引入:
1、如果张红购买了每千克1元的蔬菜x千克,
则所需的钱数
=____元.
2、如果正方形的边长为x,则面积
=_____.
3、如果正方体的边长为x,体积为y,
那么
=
4、如果一个正方形场地的面积为x,边长为y那么
=______.
5、如果某人x
秒内骑车行进了1公里,骑车的速度为y公里/秒,那么
=______
以上问题中的函数具有什么共同特征?
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。
新课
一、幂函数的概念
探究1:你能举几个学过的幂函数的例子吗?
一般地,函数
叫做幂函数,其中
是自变量,
是常数。
式子
名称
指数函数:
幂函数:
底数
指数
指数
底数
幂值
幂值
探究3:如何判断一个函数是幂函数还是指数函数?
幂函数
指数函数
探究2:你能说出幂函数与指数函数的区别吗?
看自变量
是指数还是底数
1、下面几个函数中,哪几个函数是幂函数?
答案(1)(4)(6)
练习
二、幂函数性质的探究:
探究4:结合前面指数函数与对数函数的方法,我们应如何研究幂函数呢?
作具体幂函数的图象→观察图象特征→总结函数性质
探究5:在同一坐标系中作出幂函数
的图象。
对于幂函数,我们只讨论
=1,2,3,
,–1
时的情形。
对于幂函数,我们只讨论
=1,2,3,
,–1
时的情形。
二.幂函数的图象及性质
探究6:
(探究性质)请同学们结合幂函数图象,将你发现的结论填在下面的表格内:
定义域
值
域
单调性
公共点
R
R
R
[0,+∞)
{x|
x
≠
0}
R
[0,+∞)
R
[0,+∞)
{y|
y≠
0}
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
R上是
增函数
在(-∞,0]上是减函数,在[0,
+∞)上是增函数
R上是增函数
在[0,+∞)上是增函数
在(
-∞,0)和(0,
+∞)上是减函数
(1,1)
奇偶性
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1);
三、幂函数的性质
(3)一般地,幂函数的图象在直线
的右侧,指数大的在上,指数小的在下,在
轴与直线
之间正好相反;
幂函数在第一象限内的性质
(1)-(3)
(2)如果
,则幂函数的图像都过
和
,并且在区间
上是增函数;
如果
,则幂函数的图像在区间
上是减函数,在第一
象限内,图像向上无限地逼近
轴,向右无限地逼近
轴;
如果
,则幂函数
是一条不包含(0,1)的直线
(4)幂函数图像不过第四象限。
(5)幂函数的奇偶性:
是奇函数;
是偶函数;
是非奇非偶函数。
例1:
已知幂函数的图象过点
,试求出此函数的解析式.
解:设
由题意得
总结:
(1)
理解并掌握形如
的形式就是幂函数的定义
(2)
充分理解并掌握幂函数的性质和特征
四、例题讲解
例2、下列结论中,正确的是(
)
C
A幂函数的图像都通过点(0,0),(1,1)
B幂函数的图像可以出现在第四象限
C当幂指数
取
时,幂函数
是增函数
D当幂指数
时,幂函数
在定义域上是减函数
例3、已知幂函数
的图象过点
,则
的
值(
)
A
A
B
C
D
A
B
C
D
例4、如果幂函数
的图像不过原
点,则m的取值是(
)
B
A
B
C
D
五、小
结
(1)
幂函数的定义;
(2)
5个具体幂函数的图像及性质;
(3)
幂函数的5条性质;
(4)
掌握幂函数中指数的变化对图像影响。
思考题:根据幂函数的性质画出以下函数的图像
六、作
业
1、必做:课本79页习题2.3;《优化设计》2.3幂函数95页至97页;
2、选做:《优化设计》98页能力提升第8题。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
