2021——2022学 年人教版八年级数学上册12.2三角形全等的判定 同步练习(ASA AAS)(word含答案)
文档属性
| 名称 | 2021——2022学 年人教版八年级数学上册12.2三角形全等的判定 同步练习(ASA AAS)(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:58:06 | ||
图片预览




文档简介
2021——2022学年度人教版八年级数学上册
第十二章全等三角形
12.2三角形全等的判定
同步练习3(ASA
AAS)
一、选择题
1.如图,一块三角形玻璃裂成①、②、③三块,现需要划一块同样大小的三角形玻璃,为了方便只需带上一块,号码和依据是( )
A.①SAS
B.②ASA
C.③AAS
D.③ASA
2.如图,在四边形ABCD中,AB∥DC,AD∥BC,AC与BD相交于点O,M、A、O、C、N五点在一条直线上,MB⊥BC,ND⊥DA,则图中的全等三角形共有(
)对.
A.5
B.6
C.7
D.8
3.如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是(
)
A.AAS
B.SAS
C.HL
D.SSS
4.如图,点在同一条直线上,//,//,且,若,,则EF为(
)
A.8
B.6
C.5
D.4
5.如图,如果∠A=∠D,∠1=∠2,则可判定ABC≌DCB,这是根据(
)
A.SSS
B.ASA
C.AAS
D.SAS
6.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到MBC≌ABC,所以测得MB的长就是A,B两点间的距离,这里判定MBC≌ABC的理由是(
)
A.SAS
B.AAA
C.SSS
D.ASA
7.如图,四边形ABCD中,AD∥BC,AB⊥BC,AD=6,BC=10.
DC=DE,∠CDE=90°,则△ADE的面积是( )
A.4
B.8
C.12
D.16
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,若AC=4BE,则下面结论正确的是( )
A.S△ABC=6S△BDE
B.S△ABC=7S△BDE
C.S△ABC=8S△BDE
D.S△ABC=9S△BDE
9.如图,中,垂直的平分线于点D.若的面积为a,且的面积是面积的,则的面积为(
)
A.
B.
C.
D.
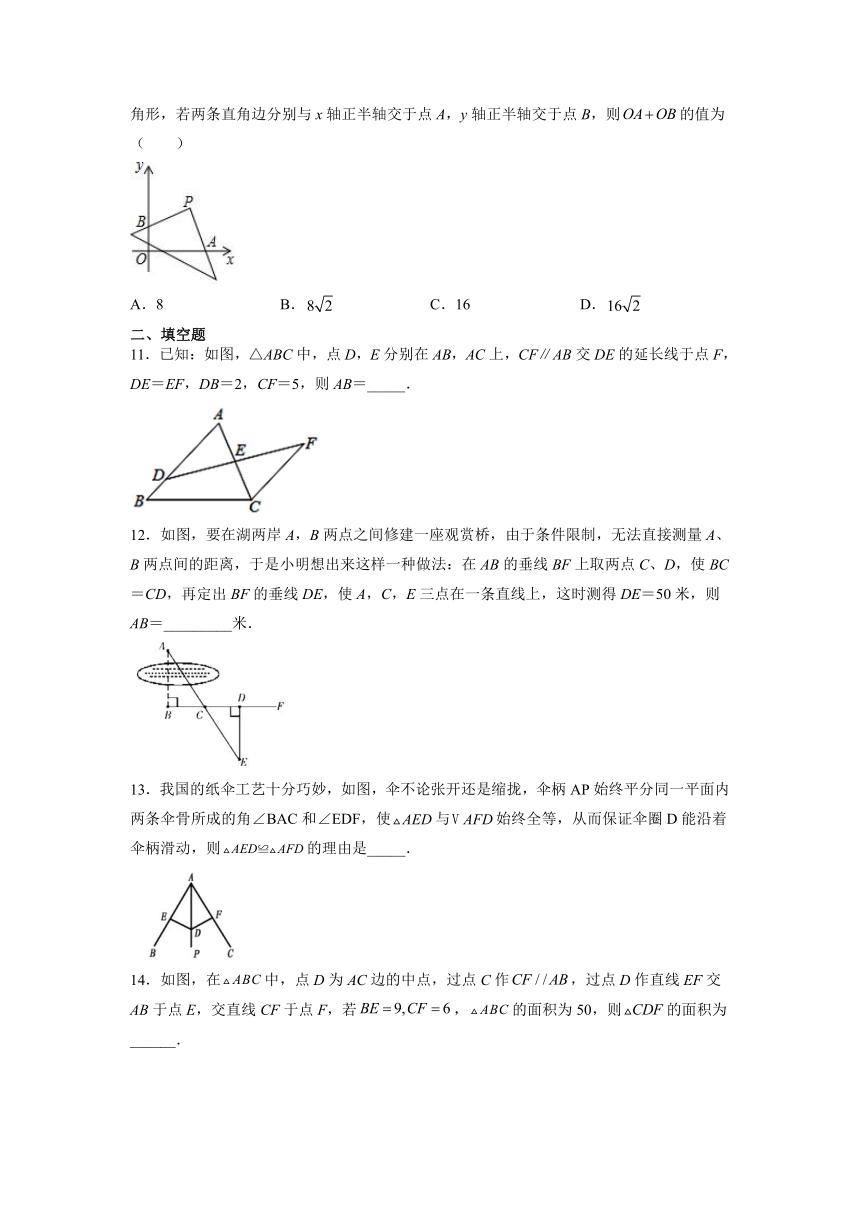
10.如图,在平面直角坐标系中,将直角三角形的直角顶点固定在点处,转动直角三角形,若两条直角边分别与x轴正半轴交于点A,y轴正半轴交于点B,则的值为(
)
A.8
B.
C.16
D.
二、填空题
11.已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=2,CF=5,则AB=_____.
12.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB=_________米.
13.我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC和∠EDF,使与始终全等,从而保证伞圈D能沿着伞柄滑动,则的理由是_____.
14.如图,在中,点D为AC边的中点,过点C作,过点D作直线EF交AB于点E,交直线CF于点F,若,的面积为50,则的面积为______.
15.为迎接全国第十四届运动会,我校举行“缓堵保畅,安全出行,小手拉大手活动”每天值班老师和部分学生在校门两边站岗执勤(线段所在区域)。如图,,与相交于,于点,,已知米,请根据上述信息求出执勤区域的长度是______.
三、解答题
16.如图是某产品商标的示意图,已知AB=CD,∠A=∠D,有人认为ABC≌DCB,他的思考过程是:
∵AB=CD,∠A=∠D,BC=CB,
∴ABC≌DCB.
你认为这个思考过程对吗?
如果正确,指出他用的是判别三角形全等的哪个条件?
如果不正确,写出你的思考过程.
17.如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=120°时,∠EDC= ;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
18.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证∶DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
19.如图,∠B=∠E,∠1=∠2,BC=EC.
求证:AB=DE.
20.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE
21.十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间的距离.
22.如图1所示,已知中,,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,求证:;
(2)若直线m绕点C旋转到图2所示的位置时(),其余条件不变,猜想与,有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时()其余条件不变,问与,的关系如何?直接写出猜想结论,不需证明.
23.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼的高度,首先他们在两栋单元楼之间选定一点,然后小华在自己家阳台处测得处的俯角为,小明站在处测得眼睛到楼端点的仰角为,发现与互余,已知米,米,米,试求单元楼的高.
【参考答案】
1.D
2.C
3.A
4.B
5.C
6.D
7.C
8.D
9.A
10.C
11.7
12.50
13.ASA
14.10
15.300m
16.解:他的思考过程不正确,
理由是:在和中,
,
,
,,
,
在和中,
,
.
17.解:(1)∠EDC=180°﹣∠BDA﹣∠ADE=180°﹣120°﹣50°=10°;
点D从B向C运动时,∠BDA逐渐变小;
故答案为10°,小;
(2)当DC等于4时,△ABD≌△DCE.
理由如下:
∵∠ADC=∠B+∠BAD,
即∠ADE+∠CDE=∠B+∠BAD,
而∠B=∠ADE=50°,
∴∠CDE=∠BAD,
在△ABD和△DCE中,
,
∴△ABD≌△DCE(ASA).
18.(1:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中
∴,
∴DE=DF;
(2解:∵
∴∠C=∠B=,
∴∠BAC=
19.证明:∵∠1=∠2
,
∴∠ACB=∠DCE,
在△ABC和△DCE中,
∴△ABC≌△DEC(AAS),
∴AB=DE.
20.证明:在△ABE和△ACD中,
∵,
△ABE≌△ACD
(ASA),
∴AE=AD,
∴BD=AB–AD=AC-AE=CE.
21.(1)证明:由题意得:,,
∴,
∴,
∴
在和中
,
∴;
(2)解:由题意得:,
∵,
∴,
∴,
答:两堵木墙之间的距离为.
22.(1)证明:,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(2)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(3)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴.
23.解:过点F作FG⊥AB于点G,则FG=BE=20(米),
∵BE=CD,
∴FG=CD,
∵+=90°,
又∵∠1+∠ECD=90°,
∴∠2=∠ECD,
在和中,
∴(AAS),
∴AG=DE=BD-GF=58-20=38(米),
又∵BG=EF=1(米),
∴AB=AG+BG=38+1=39(米).
答:单元楼的高为39米.
第十二章全等三角形
12.2三角形全等的判定
同步练习3(ASA
AAS)
一、选择题
1.如图,一块三角形玻璃裂成①、②、③三块,现需要划一块同样大小的三角形玻璃,为了方便只需带上一块,号码和依据是( )
A.①SAS
B.②ASA
C.③AAS
D.③ASA
2.如图,在四边形ABCD中,AB∥DC,AD∥BC,AC与BD相交于点O,M、A、O、C、N五点在一条直线上,MB⊥BC,ND⊥DA,则图中的全等三角形共有(
)对.
A.5
B.6
C.7
D.8
3.如图,在△ABC中,∠B=∠C,D为BC中点,若由点D分别向AB、AC作垂线段DE、DF,则能说明△BDE≌△CDF的理由是(
)
A.AAS
B.SAS
C.HL
D.SSS
4.如图,点在同一条直线上,//,//,且,若,,则EF为(
)
A.8
B.6
C.5
D.4
5.如图,如果∠A=∠D,∠1=∠2,则可判定ABC≌DCB,这是根据(
)
A.SSS
B.ASA
C.AAS
D.SAS
6.如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=75°,∠ACB=35°,然后在M处立了标杆,使∠CBM=75°,∠MCB=35°,得到MBC≌ABC,所以测得MB的长就是A,B两点间的距离,这里判定MBC≌ABC的理由是(
)
A.SAS
B.AAA
C.SSS
D.ASA
7.如图,四边形ABCD中,AD∥BC,AB⊥BC,AD=6,BC=10.
DC=DE,∠CDE=90°,则△ADE的面积是( )
A.4
B.8
C.12
D.16
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,若AC=4BE,则下面结论正确的是( )
A.S△ABC=6S△BDE
B.S△ABC=7S△BDE
C.S△ABC=8S△BDE
D.S△ABC=9S△BDE
9.如图,中,垂直的平分线于点D.若的面积为a,且的面积是面积的,则的面积为(
)
A.
B.
C.
D.
10.如图,在平面直角坐标系中,将直角三角形的直角顶点固定在点处,转动直角三角形,若两条直角边分别与x轴正半轴交于点A,y轴正半轴交于点B,则的值为(
)
A.8
B.
C.16
D.
二、填空题
11.已知:如图,△ABC中,点D,E分别在AB,AC上,CF∥AB交DE的延长线于点F,DE=EF,DB=2,CF=5,则AB=_____.
12.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB=_________米.
13.我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC和∠EDF,使与始终全等,从而保证伞圈D能沿着伞柄滑动,则的理由是_____.
14.如图,在中,点D为AC边的中点,过点C作,过点D作直线EF交AB于点E,交直线CF于点F,若,的面积为50,则的面积为______.
15.为迎接全国第十四届运动会,我校举行“缓堵保畅,安全出行,小手拉大手活动”每天值班老师和部分学生在校门两边站岗执勤(线段所在区域)。如图,,与相交于,于点,,已知米,请根据上述信息求出执勤区域的长度是______.
三、解答题
16.如图是某产品商标的示意图,已知AB=CD,∠A=∠D,有人认为ABC≌DCB,他的思考过程是:
∵AB=CD,∠A=∠D,BC=CB,
∴ABC≌DCB.
你认为这个思考过程对吗?
如果正确,指出他用的是判别三角形全等的哪个条件?
如果不正确,写出你的思考过程.
17.如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=120°时,∠EDC= ;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由.
18.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证∶DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
19.如图,∠B=∠E,∠1=∠2,BC=EC.
求证:AB=DE.
20.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE
21.十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间的距离.
22.如图1所示,已知中,,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,求证:;
(2)若直线m绕点C旋转到图2所示的位置时(),其余条件不变,猜想与,有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时()其余条件不变,问与,的关系如何?直接写出猜想结论,不需证明.
23.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼的高度,首先他们在两栋单元楼之间选定一点,然后小华在自己家阳台处测得处的俯角为,小明站在处测得眼睛到楼端点的仰角为,发现与互余,已知米,米,米,试求单元楼的高.
【参考答案】
1.D
2.C
3.A
4.B
5.C
6.D
7.C
8.D
9.A
10.C
11.7
12.50
13.ASA
14.10
15.300m
16.解:他的思考过程不正确,
理由是:在和中,
,
,
,,
,
在和中,
,
.
17.解:(1)∠EDC=180°﹣∠BDA﹣∠ADE=180°﹣120°﹣50°=10°;
点D从B向C运动时,∠BDA逐渐变小;
故答案为10°,小;
(2)当DC等于4时,△ABD≌△DCE.
理由如下:
∵∠ADC=∠B+∠BAD,
即∠ADE+∠CDE=∠B+∠BAD,
而∠B=∠ADE=50°,
∴∠CDE=∠BAD,
在△ABD和△DCE中,
,
∴△ABD≌△DCE(ASA).
18.(1:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中
∴,
∴DE=DF;
(2解:∵
∴∠C=∠B=,
∴∠BAC=
19.证明:∵∠1=∠2
,
∴∠ACB=∠DCE,
在△ABC和△DCE中,
∴△ABC≌△DEC(AAS),
∴AB=DE.
20.证明:在△ABE和△ACD中,
∵,
△ABE≌△ACD
(ASA),
∴AE=AD,
∴BD=AB–AD=AC-AE=CE.
21.(1)证明:由题意得:,,
∴,
∴,
∴
在和中
,
∴;
(2)解:由题意得:,
∵,
∴,
∴,
答:两堵木墙之间的距离为.
22.(1)证明:,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(2)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴;
(3)解:,理由如下:
,,,
,
,,
,
在和中,
,
,
,,
∵,
∴.
23.解:过点F作FG⊥AB于点G,则FG=BE=20(米),
∵BE=CD,
∴FG=CD,
∵+=90°,
又∵∠1+∠ECD=90°,
∴∠2=∠ECD,
在和中,
∴(AAS),
∴AG=DE=BD-GF=58-20=38(米),
又∵BG=EF=1(米),
∴AB=AG+BG=38+1=39(米).
答:单元楼的高为39米.
