陕西省渭南市韩城市象山高级中学校2020-2021学年高二下学期期中考试理科数学试题(Word版含答案)
文档属性
| 名称 | 陕西省渭南市韩城市象山高级中学校2020-2021学年高二下学期期中考试理科数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 508.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 12:47:26 | ||
图片预览




文档简介
象山中学2020-2021学年度第二学期期中试题
高二理数试卷
一、选择题:(本大题共12小题,每题5分,共60分)
1.
中,可表示为(
)
A.
B.
C.
D.
2.
在复平面内,复数与分别对应向量和,其中O坐标原点,则=(
)
A.
B.
C.
2
D.
4
3.
曲线在点处切线方程为
A.
B.
C.
D.
4.
某学生解选择题出错的概率为0.1,该生解三道选择题至少有一道出错的概率是(
)
A.
B.
C.
D.
5.
随机变量的概率分布列规律为其中为常数,则
的值为
.
A.
B.
C.
D.
6.
A.
B.
C.
D.
7.
如图所示,函数的图象在点处的切线方程是则(
)
A.
B.
1
C.
2
D.
0
8.
我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有(
)
A.
58
B.
59
C.
60
D.
61
9.
令为的展开式中含项的系数,则数列的前n项和为(
)
A.
B.
C.
D.
10.
从6名团员中选出4人分别担任书记、副书记、宣传委员、组织委员四项职务,若其中甲、乙不能担任书记,则不同的任职方案种数是( )
A.
280
B.
240
C.
180
D.
96
11.
已知函数.若的最小值为,且对任意的恒成立,则实数m的取值围是(
)
A.
B.
C.
D.
12.
已知对任意实数都有,,若不等式(其中)的解集中恰有两个整数,则的取值范围是(
)
A.
B.
C.
D.
二、填空题:(本大题共4小题,每小题5分,共20分)
13.
设随机变量,且,则____________.
14.
函数在区间上的最大值是_____.
15.
10名同学合影,站成了前排3人,后排7人,现摄影师要从后排7人中抽2人站前排,其他人的相对顺序不变,则不同的调整方法的种数为_______(用数字作答).
16.
利用证明“”时,从假设推证成立时,可以在时左边的表达式上再乘一个因式,多乘的这个因式为_______.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知二项式展开式中各项系数之和比各二项式系数之和大240,
(1)求展开式中含x项的系数;
(2)求展开式中所有含x的有理项.
18.
3名男生,4名女生,按照不同的要求排队.求不同的排队方案的方法种数.(列式并算出答案)
(1)选其中5人排成一排:
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,甲不站排头也不站排尾.
19.
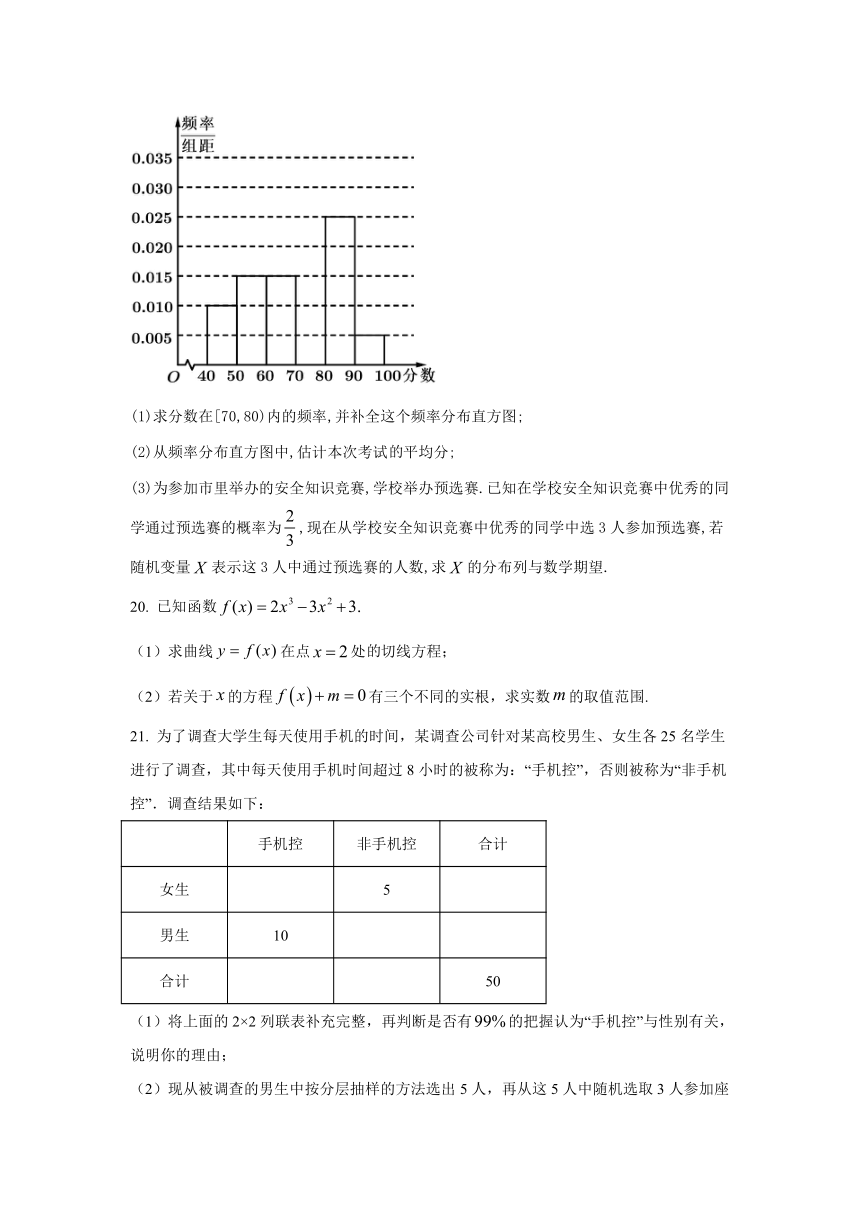
学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量表示这3人中通过预选赛的人数,求的分布列与数学期望.
20.
已知函数
(1)求曲线在点处切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
21.
为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的2×2列联表补充完整,再判断是否有的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.
参考公式:,其中
参考数据:
0.10
0.05
0.010
0.001
2.706
3.841
6635
10.828
22.
已知函数.
(1)求函数的单调区间;
(2)若,求证:
.(为自然对数的底数)
象山中学2020-2021学年度第二学期期中试题
高二理数试卷
答案版
一、选择题:(本大题共12小题,每题5分,共60分)
1.
中,可表示为(
)
A.
B.
C.
D.
答案:B
2.
在复平面内,复数与分别对应向量和,其中O坐标原点,则=(
)
A.
B.
C.
2
D.
4
答案:C
3.
曲线在点处切线方程为
A.
B.
C.
D.
答案:A
4.
某学生解选择题出错的概率为0.1,该生解三道选择题至少有一道出错的概率是(
)
A.
B.
C.
D.
答案:C
5.
随机变量的概率分布列规律为其中为常数,则的值为
.
A.
B.
C.
D.
答案:D
6.
A.
B.
C.
D.
答案:D
7.
如图所示,函数的图象在点处的切线方程是则(
)
A.
B.
1
C.
2
D.
0
答案:B
8.
我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有(
)
A.
58
B.
59
C.
60
D.
61
答案:C
9.
令为的展开式中含项的系数,则数列的前n项和为(
)
A.
B.
C.
D.
答案:D
10.
从6名团员中选出4人分别担任书记、副书记、宣传委员、组织委员四项职务,若其中甲、乙不能担任书记,则不同的任职方案种数是( )
A.
280
B.
240
C.
180
D.
96
答案:B
11.
已知函数.若的最小值为,且对任意的恒成立,则实数m的取值围是(
)
A.
B.
C.
D.
答案:C
12.
已知对任意实数都有,,若不等式(其中)的解集中恰有两个整数,则的取值范围是(
)
A.
B.
C.
D.
答案:C
二、填空题:(本大题共4小题,每小题5分,共20分)
13.
设随机变量,且,则____________.
答案:0.3
14.
函数在区间上的最大值是_____.
答案:
15.
10名同学合影,站成了前排3人,后排7人,现摄影师要从后排7人中抽2人站前排,其他人的相对顺序不变,则不同的调整方法的种数为_______(用数字作答).
答案:420
16.
利用证明“”时,从假设推证成立时,可以在时左边的表达式上再乘一个因式,多乘的这个因式为_______.
答案:.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知二项式展开式中各项系数之和比各二项式系数之和大240,
(1)求展开式中含x项的系数;
(2)求展开式中所有含x的有理项.
答案:(1)150;(2),,.
18.
3名男生,4名女生,按照不同的要求排队.求不同的排队方案的方法种数.(列式并算出答案)
(1)选其中5人排成一排:
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,甲不站排头也不站排尾.
答案:(1)2520;(2)288;(3)1440;(4)3600.
19.
学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量表示这3人中通过预选赛的人数,求的分布列与数学期望.
答案:(1)
0.3;(2);(3)
分布列见解析,.
20.
已知函数
(1)求曲线在点处切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
答案:(1)12x﹣y﹣17=0(2)(﹣3,﹣2)
21.
为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的2×2列联表补充完整,再判断是否有的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.
参考公式:,其中
参考数据:
0.10
0.05
0.010
0.001
2.706
3.841
6635
10.828
答案:(1)列联表详见解析,有的把握认为“手机控”与性别有关;
(2)
分布列详见解析,;
22.
已知函数.
(1)求函数的单调区间;
(2)若,求证:
.(为自然对数的底数)
答案:(1)当时,
只有增区间为,当时,
的增区间为,减区间为;(2)证明见解析.
高二理数试卷
一、选择题:(本大题共12小题,每题5分,共60分)
1.
中,可表示为(
)
A.
B.
C.
D.
2.
在复平面内,复数与分别对应向量和,其中O坐标原点,则=(
)
A.
B.
C.
2
D.
4
3.
曲线在点处切线方程为
A.
B.
C.
D.
4.
某学生解选择题出错的概率为0.1,该生解三道选择题至少有一道出错的概率是(
)
A.
B.
C.
D.
5.
随机变量的概率分布列规律为其中为常数,则
的值为
.
A.
B.
C.
D.
6.
A.
B.
C.
D.
7.
如图所示,函数的图象在点处的切线方程是则(
)
A.
B.
1
C.
2
D.
0
8.
我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有(
)
A.
58
B.
59
C.
60
D.
61
9.
令为的展开式中含项的系数,则数列的前n项和为(
)
A.
B.
C.
D.
10.
从6名团员中选出4人分别担任书记、副书记、宣传委员、组织委员四项职务,若其中甲、乙不能担任书记,则不同的任职方案种数是( )
A.
280
B.
240
C.
180
D.
96
11.
已知函数.若的最小值为,且对任意的恒成立,则实数m的取值围是(
)
A.
B.
C.
D.
12.
已知对任意实数都有,,若不等式(其中)的解集中恰有两个整数,则的取值范围是(
)
A.
B.
C.
D.
二、填空题:(本大题共4小题,每小题5分,共20分)
13.
设随机变量,且,则____________.
14.
函数在区间上的最大值是_____.
15.
10名同学合影,站成了前排3人,后排7人,现摄影师要从后排7人中抽2人站前排,其他人的相对顺序不变,则不同的调整方法的种数为_______(用数字作答).
16.
利用证明“”时,从假设推证成立时,可以在时左边的表达式上再乘一个因式,多乘的这个因式为_______.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知二项式展开式中各项系数之和比各二项式系数之和大240,
(1)求展开式中含x项的系数;
(2)求展开式中所有含x的有理项.
18.
3名男生,4名女生,按照不同的要求排队.求不同的排队方案的方法种数.(列式并算出答案)
(1)选其中5人排成一排:
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,甲不站排头也不站排尾.
19.
学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量表示这3人中通过预选赛的人数,求的分布列与数学期望.
20.
已知函数
(1)求曲线在点处切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
21.
为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的2×2列联表补充完整,再判断是否有的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.
参考公式:,其中
参考数据:
0.10
0.05
0.010
0.001
2.706
3.841
6635
10.828
22.
已知函数.
(1)求函数的单调区间;
(2)若,求证:
.(为自然对数的底数)
象山中学2020-2021学年度第二学期期中试题
高二理数试卷
答案版
一、选择题:(本大题共12小题,每题5分,共60分)
1.
中,可表示为(
)
A.
B.
C.
D.
答案:B
2.
在复平面内,复数与分别对应向量和,其中O坐标原点,则=(
)
A.
B.
C.
2
D.
4
答案:C
3.
曲线在点处切线方程为
A.
B.
C.
D.
答案:A
4.
某学生解选择题出错的概率为0.1,该生解三道选择题至少有一道出错的概率是(
)
A.
B.
C.
D.
答案:C
5.
随机变量的概率分布列规律为其中为常数,则的值为
.
A.
B.
C.
D.
答案:D
6.
A.
B.
C.
D.
答案:D
7.
如图所示,函数的图象在点处的切线方程是则(
)
A.
B.
1
C.
2
D.
0
答案:B
8.
我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有(
)
A.
58
B.
59
C.
60
D.
61
答案:C
9.
令为的展开式中含项的系数,则数列的前n项和为(
)
A.
B.
C.
D.
答案:D
10.
从6名团员中选出4人分别担任书记、副书记、宣传委员、组织委员四项职务,若其中甲、乙不能担任书记,则不同的任职方案种数是( )
A.
280
B.
240
C.
180
D.
96
答案:B
11.
已知函数.若的最小值为,且对任意的恒成立,则实数m的取值围是(
)
A.
B.
C.
D.
答案:C
12.
已知对任意实数都有,,若不等式(其中)的解集中恰有两个整数,则的取值范围是(
)
A.
B.
C.
D.
答案:C
二、填空题:(本大题共4小题,每小题5分,共20分)
13.
设随机变量,且,则____________.
答案:0.3
14.
函数在区间上的最大值是_____.
答案:
15.
10名同学合影,站成了前排3人,后排7人,现摄影师要从后排7人中抽2人站前排,其他人的相对顺序不变,则不同的调整方法的种数为_______(用数字作答).
答案:420
16.
利用证明“”时,从假设推证成立时,可以在时左边的表达式上再乘一个因式,多乘的这个因式为_______.
答案:.
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.
已知二项式展开式中各项系数之和比各二项式系数之和大240,
(1)求展开式中含x项的系数;
(2)求展开式中所有含x的有理项.
答案:(1)150;(2),,.
18.
3名男生,4名女生,按照不同的要求排队.求不同的排队方案的方法种数.(列式并算出答案)
(1)选其中5人排成一排:
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,甲不站排头也不站排尾.
答案:(1)2520;(2)288;(3)1440;(4)3600.
19.
学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量表示这3人中通过预选赛的人数,求的分布列与数学期望.
答案:(1)
0.3;(2);(3)
分布列见解析,.
20.
已知函数
(1)求曲线在点处切线方程;
(2)若关于的方程有三个不同的实根,求实数的取值范围.
答案:(1)12x﹣y﹣17=0(2)(﹣3,﹣2)
21.
为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的2×2列联表补充完整,再判断是否有的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为X,试求X的分布列与数学期望.
参考公式:,其中
参考数据:
0.10
0.05
0.010
0.001
2.706
3.841
6635
10.828
答案:(1)列联表详见解析,有的把握认为“手机控”与性别有关;
(2)
分布列详见解析,;
22.
已知函数.
(1)求函数的单调区间;
(2)若,求证:
.(为自然对数的底数)
答案:(1)当时,
只有增区间为,当时,
的增区间为,减区间为;(2)证明见解析.
同课章节目录
