2021-2022学年北师大版九年级数学上册4.4.4黄金分割 同步练习题(word含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4.4黄金分割 同步练习题(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 78.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 18:52:15 | ||
图片预览


文档简介
4.4.4黄金分割同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为______米.
2.大自然巧夺天工,一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8
cm,那么AB的长度为______.
3.如图,C,D是线段AB的两个黄金分割点,则的值为______.
二、选择题
4.已知点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是(
)
A.如果=,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
5.已知点P是线段AB的黄金分割点,且AP>BP,则下列各式不正确的是(
)
A.AP∶BP=AB∶AP02
B.AP=AB
C.BP=AB
D.AP≈0.618AB
6.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是(
)
A.=
B.=
C.=
D.=
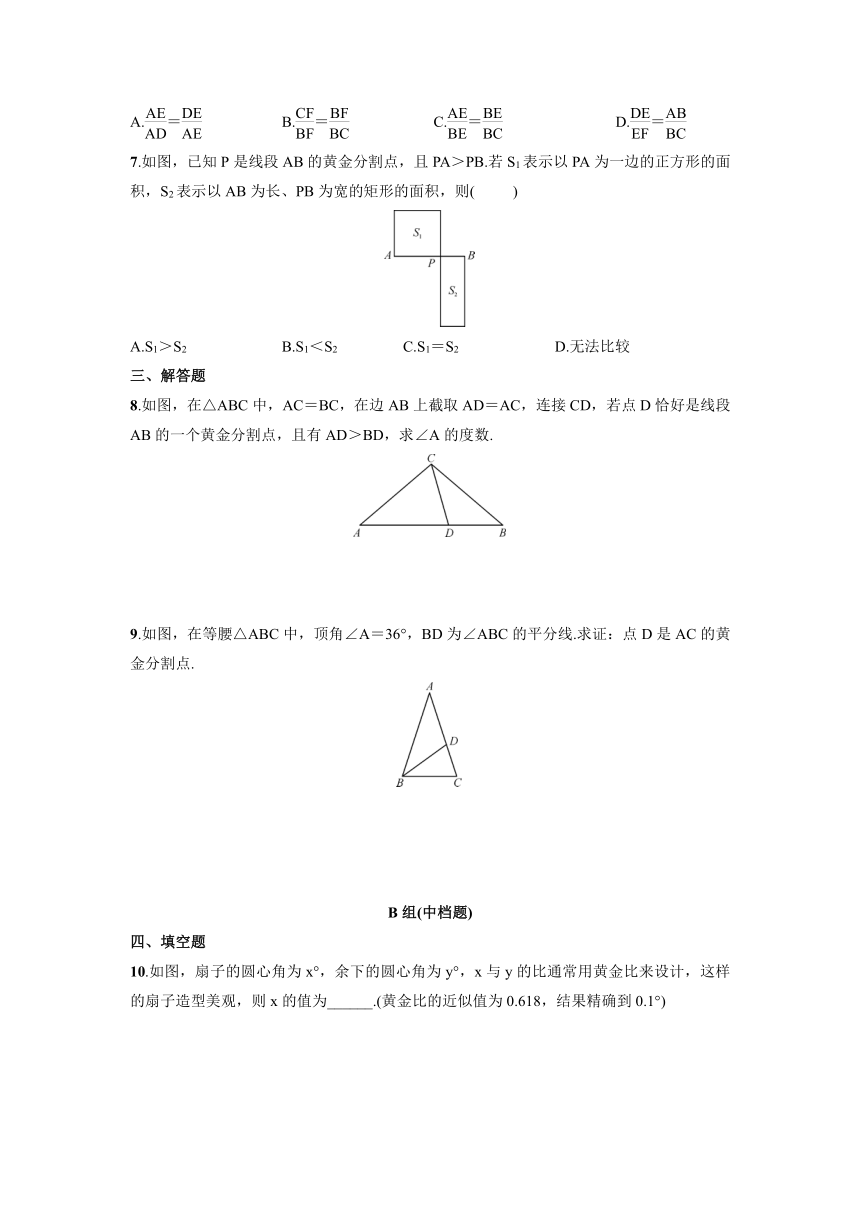
7.如图,已知P是线段AB的黄金分割点,且PA>PB.若S1表示以PA为一边的正方形的面积,S2表示以AB为长、PB为宽的矩形的面积,则(
)
A.S1>S2
B.S1<S2
C.S1=S2
D.无法比较
三、解答题
8.如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,且有AD>BD,求∠A的度数.
9.如图,在等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线.求证:点D是AC的黄金分割点.
B组(中档题)
四、填空题
10.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为______.(黄金比的近似值为0.618,结果精确到0.1°)
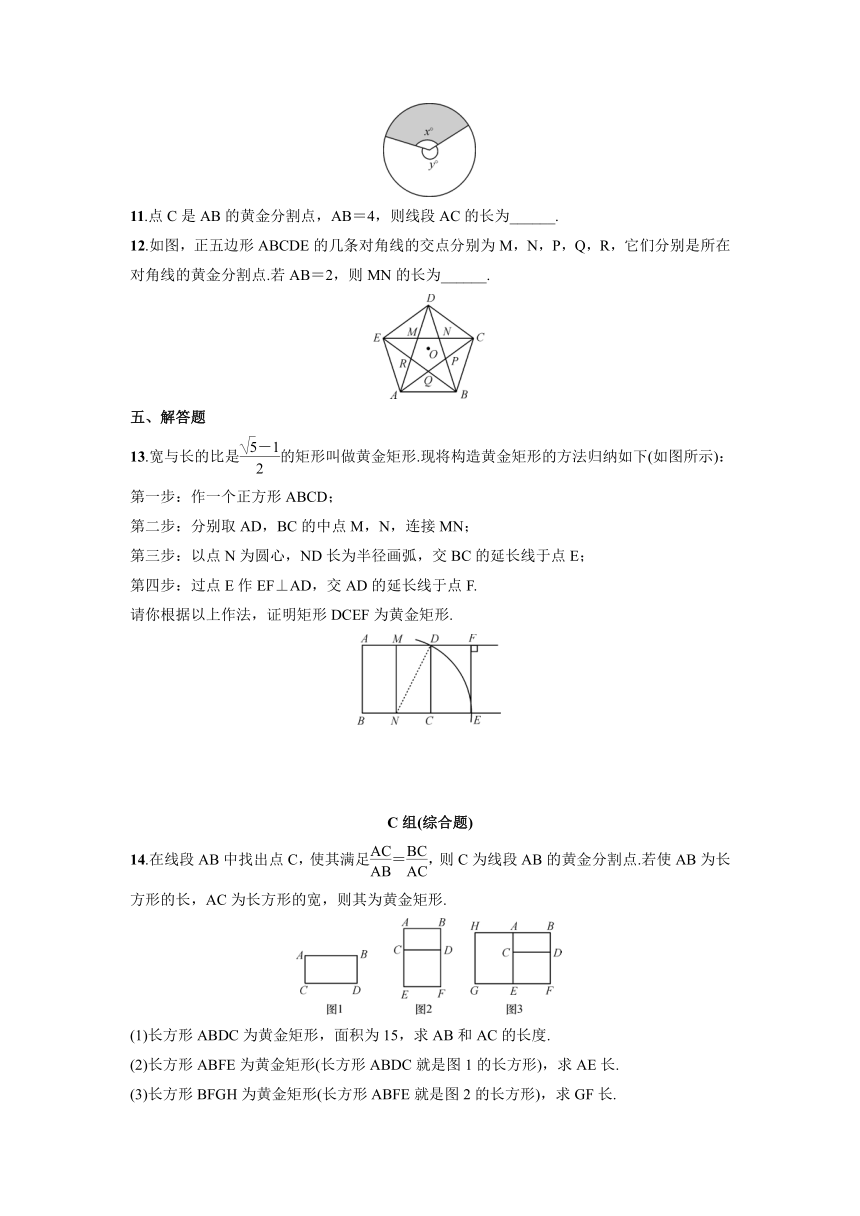
11.点C是AB的黄金分割点,AB=4,则线段AC的长为______.
12.如图,正五边形ABCDE的几条对角线的交点分别为M,N,P,Q,R,它们分别是所在对角线的黄金分割点.若AB=2,则MN的长为______.
五、解答题
13.宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
C组(综合题)
14.在线段AB中找出点C,使其满足=,则C为线段AB的黄金分割点.若使AB为长方形的长,AC为长方形的宽,则其为黄金矩形.
(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度.
(2)长方形ABFE为黄金矩形(长方形ABDC就是图1的长方形),求AE长.
(3)长方形BFGH为黄金矩形(长方形ABFE就是图2的长方形),求GF长.
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个……则求第十个这样的黄金矩形的长为______.
参考答案
4.4.4黄金分割同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为1.24米.
2.大自然巧夺天工,一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8
cm,那么AB的长度为(4+4)cm.
3.如图,C,D是线段AB的两个黄金分割点,则的值为-2.
二、选择题
4.已知点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是(
C
)
A.如果=,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
5.已知点P是线段AB的黄金分割点,且AP>BP,则下列各式不正确的是(
C
)
A.AP∶BP=AB∶AP02
B.AP=AB
C.BP=AB
D.AP≈0.618AB
6.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是(
C
)
A.=
B.=
C.=
D.=
7.如图,已知P是线段AB的黄金分割点,且PA>PB.若S1表示以PA为一边的正方形的面积,S2表示以AB为长、PB为宽的矩形的面积,则(
C
)
A.S1>S2
B.S1<S2
C.S1=S2
D.无法比较
三、解答题
8.如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,且有AD>BD,求∠A的度数.
解:∵点D是线段AB的一个黄金分割点,且AD>BD,
∴AD2=BD·AB.
∵AD=AC=BC,
∴BC2=BD·AB,即BC∶BD=AB∶BC.
∵∠CBD=∠ABC,
∴△BCD∽△BAC.∴∠A=∠BCD.
∵AC=BC,∴∠A=∠B.
设∠A=x°,则∠B=x°,∠BCD=x°,
∴∠ADC=∠BCD+∠B=2x°.
∵AC=AD,∴∠ACD=∠ADC=2x°.
在△ABC中,x+(2x+x)+x=180,
解得x=36,∴∠A=36°.
9.如图,在等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线.求证:点D是AC的黄金分割点.
解:在等腰△ABC中,顶角∠A=36°,
∴∠ABC=∠C=72°.
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°.
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD.
∴AC∶BC=BC∶DC.
∵∠A=∠ABD,∴AD=BD.
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°.∴BD=BC.
∴AD=BC.
∴AC∶AD=AD∶DC,即点D是AC的黄金分割点.
B组(中档题)
四、填空题
10.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为138°.(黄金比的近似值为0.618,结果精确到0.1°)
11.点C是AB的黄金分割点,AB=4,则线段AC的长为2-2或6-2.
12.如图,正五边形ABCDE的几条对角线的交点分别为M,N,P,Q,R,它们分别是所在对角线的黄金分割点.若AB=2,则MN的长为3-.
五、解答题
13.宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
证明:在正方形ABCD中,设AB=2a.
∵N为BC的中点,
∴NC=BC=a.
在Rt△DNC中,
ND===a.
又∵NE=ND,∴CE=NE-NC=(-1)a.
∴==,即矩形DCEF为黄金矩形.
C组(综合题)
14.在线段AB中找出点C,使其满足=,则C为线段AB的黄金分割点.若使AB为长方形的长,AC为长方形的宽,则其为黄金矩形.
(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度.
(2)长方形ABFE为黄金矩形(长方形ABDC就是图1的长方形),求AE长.
(3)长方形BFGH为黄金矩形(长方形ABFE就是图2的长方形),求GF长.
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个……则求第十个这样的黄金矩形的长为()9×.
解:(1)设AB=x,则AC=x,
x·x=15,解得x=±(负值舍去).
∴AB=,AC=×=.
(2)由题意,得=,又由(1)得AB=,
∴AE==×=.
(3)由题意,得=,由(2)得BF=AE=,
∴GF=BF=×=.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为______米.
2.大自然巧夺天工,一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8
cm,那么AB的长度为______.
3.如图,C,D是线段AB的两个黄金分割点,则的值为______.
二、选择题
4.已知点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是(
)
A.如果=,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
5.已知点P是线段AB的黄金分割点,且AP>BP,则下列各式不正确的是(
)
A.AP∶BP=AB∶AP02
B.AP=AB
C.BP=AB
D.AP≈0.618AB
6.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是(
)
A.=
B.=
C.=
D.=
7.如图,已知P是线段AB的黄金分割点,且PA>PB.若S1表示以PA为一边的正方形的面积,S2表示以AB为长、PB为宽的矩形的面积,则(
)
A.S1>S2
B.S1<S2
C.S1=S2
D.无法比较
三、解答题
8.如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,且有AD>BD,求∠A的度数.
9.如图,在等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线.求证:点D是AC的黄金分割点.
B组(中档题)
四、填空题
10.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为______.(黄金比的近似值为0.618,结果精确到0.1°)
11.点C是AB的黄金分割点,AB=4,则线段AC的长为______.
12.如图,正五边形ABCDE的几条对角线的交点分别为M,N,P,Q,R,它们分别是所在对角线的黄金分割点.若AB=2,则MN的长为______.
五、解答题
13.宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
C组(综合题)
14.在线段AB中找出点C,使其满足=,则C为线段AB的黄金分割点.若使AB为长方形的长,AC为长方形的宽,则其为黄金矩形.
(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度.
(2)长方形ABFE为黄金矩形(长方形ABDC就是图1的长方形),求AE长.
(3)长方形BFGH为黄金矩形(长方形ABFE就是图2的长方形),求GF长.
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个……则求第十个这样的黄金矩形的长为______.
参考答案
4.4.4黄金分割同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为1.24米.
2.大自然巧夺天工,一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8
cm,那么AB的长度为(4+4)cm.
3.如图,C,D是线段AB的两个黄金分割点,则的值为-2.
二、选择题
4.已知点C把线段AB分成两条线段AC,BC,且AC>BC,下列说法错误的是(
C
)
A.如果=,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
5.已知点P是线段AB的黄金分割点,且AP>BP,则下列各式不正确的是(
C
)
A.AP∶BP=AB∶AP02
B.AP=AB
C.BP=AB
D.AP≈0.618AB
6.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是(
C
)
A.=
B.=
C.=
D.=
7.如图,已知P是线段AB的黄金分割点,且PA>PB.若S1表示以PA为一边的正方形的面积,S2表示以AB为长、PB为宽的矩形的面积,则(
C
)
A.S1>S2
B.S1<S2
C.S1=S2
D.无法比较
三、解答题
8.如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,且有AD>BD,求∠A的度数.
解:∵点D是线段AB的一个黄金分割点,且AD>BD,
∴AD2=BD·AB.
∵AD=AC=BC,
∴BC2=BD·AB,即BC∶BD=AB∶BC.
∵∠CBD=∠ABC,
∴△BCD∽△BAC.∴∠A=∠BCD.
∵AC=BC,∴∠A=∠B.
设∠A=x°,则∠B=x°,∠BCD=x°,
∴∠ADC=∠BCD+∠B=2x°.
∵AC=AD,∴∠ACD=∠ADC=2x°.
在△ABC中,x+(2x+x)+x=180,
解得x=36,∴∠A=36°.
9.如图,在等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线.求证:点D是AC的黄金分割点.
解:在等腰△ABC中,顶角∠A=36°,
∴∠ABC=∠C=72°.
∵BD为∠ABC的平分线,
∴∠ABD=∠DBC=36°.
∵∠C=∠C,∠A=∠CBD=36°,
∴△ACB∽△BCD.
∴AC∶BC=BC∶DC.
∵∠A=∠ABD,∴AD=BD.
∵∠DBC=36°,∠C=72°,
∴∠BDC=72°.∴BD=BC.
∴AD=BC.
∴AC∶AD=AD∶DC,即点D是AC的黄金分割点.
B组(中档题)
四、填空题
10.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为138°.(黄金比的近似值为0.618,结果精确到0.1°)
11.点C是AB的黄金分割点,AB=4,则线段AC的长为2-2或6-2.
12.如图,正五边形ABCDE的几条对角线的交点分别为M,N,P,Q,R,它们分别是所在对角线的黄金分割点.若AB=2,则MN的长为3-.
五、解答题
13.宽与长的比是的矩形叫做黄金矩形.现将构造黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于点F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
证明:在正方形ABCD中,设AB=2a.
∵N为BC的中点,
∴NC=BC=a.
在Rt△DNC中,
ND===a.
又∵NE=ND,∴CE=NE-NC=(-1)a.
∴==,即矩形DCEF为黄金矩形.
C组(综合题)
14.在线段AB中找出点C,使其满足=,则C为线段AB的黄金分割点.若使AB为长方形的长,AC为长方形的宽,则其为黄金矩形.
(1)长方形ABDC为黄金矩形,面积为15,求AB和AC的长度.
(2)长方形ABFE为黄金矩形(长方形ABDC就是图1的长方形),求AE长.
(3)长方形BFGH为黄金矩形(长方形ABFE就是图2的长方形),求GF长.
(4)若继续按下面的方法画下去,可以得到第四个、第五个、第六个……则求第十个这样的黄金矩形的长为()9×.
解:(1)设AB=x,则AC=x,
x·x=15,解得x=±(负值舍去).
∴AB=,AC=×=.
(2)由题意,得=,又由(1)得AB=,
∴AE==×=.
(3)由题意,得=,由(2)得BF=AE=,
∴GF=BF=×=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
