2021-2022学年北师大版八年级数学上册第1章 勾股定理 单元训练 (word含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第1章 勾股定理 单元训练 (word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 320.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 18:56:41 | ||
图片预览


文档简介
2021-2022北师大版八年级数学上册《第1章勾股定理》同步优生辅导训练(附答案)
1.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5
B.7
C.13
D.15
2.下列各组数中是勾股数的是( )
A.5,12,13
B.7,23,25
C.2,2,3
D.
3.以下列各组数的长度围成的三角形中,不是直角三角形的一组是( )
A.6,8,11
B.5,12,13
C.25,7,24
D.3,4,5
4.下列条件中不能判断△ABC是直角三角形的是( )
A.a:b:c=7:24:25
B.∠B﹣∠C=∠A
C.∠A:∠B:∠C=6:8:10
D.a2=(b+c)(b﹣c)
5.如图,一块三角形木板,测得AB=13,BC=5,AC=12,则三角形木板ABC的面积为( )
A.60
B.30
C.65
D.不能确定
6.直角三角形的边长分别为a,b,c,若a2=9,b2=16,那么c2的值是( )
A.25
B.49
C.25或7
D.25或49
7.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2
B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2
D.x2+92=(20﹣x)2
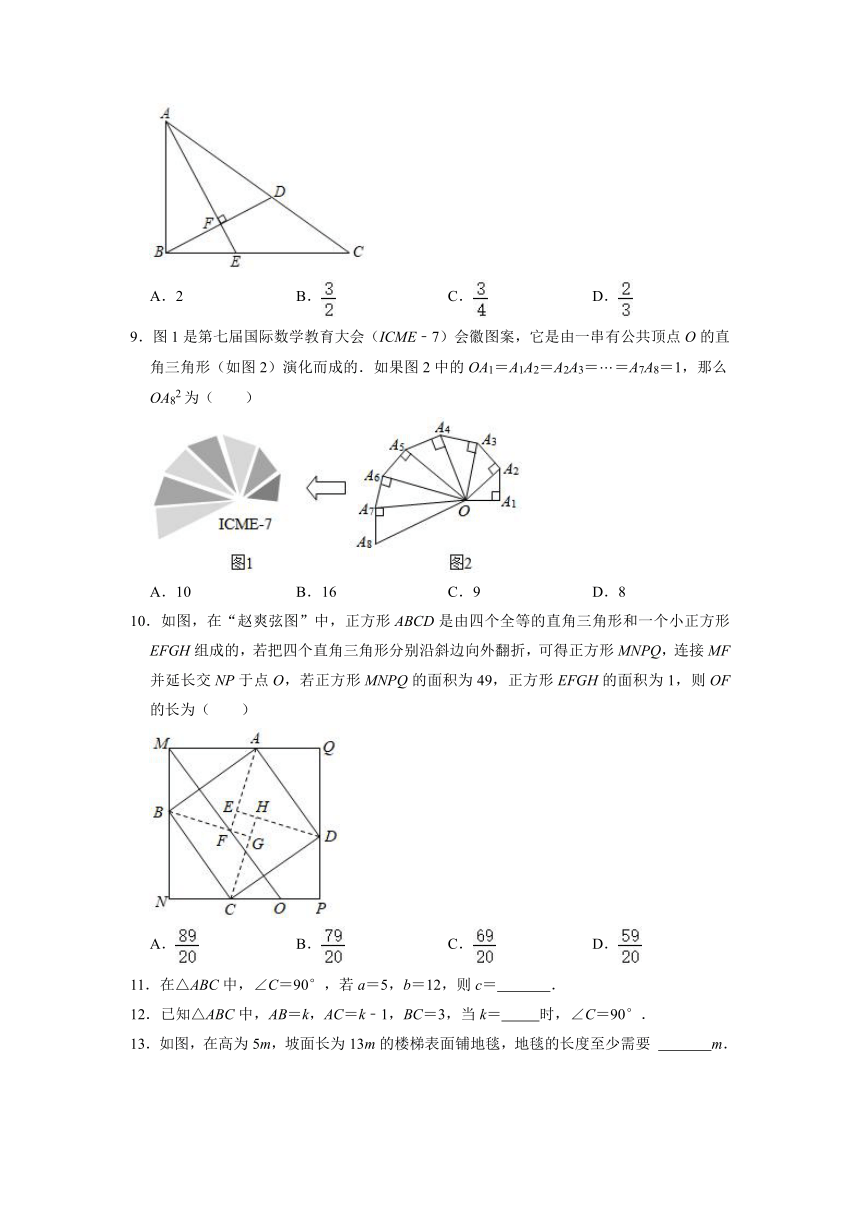
8.如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点D在边AC上,AD=AB,AE⊥BD,垂足为点F,交BC于点E,则BE的长为( )
A.2
B.
C.
D.
9.图1是第七届国际数学教育大会(ICME﹣7)会徽图案,它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的OA1=A1A2=A2A3=?=A7A8=1,那么OA82为( )
A.10
B.16
C.9
D.8
10.如图,在“赵爽弦图”中,正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成的,若把四个直角三角形分别沿斜边向外翻折,可得正方形MNPQ,连接MF并延长交NP于点O,若正方形MNPQ的面积为49,正方形EFGH的面积为1,则OF的长为( )
A.
B.
C.
D.
11.在△ABC中,∠C=90°,若a=5,b=12,则c=
.
12.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k=
时,∠C=90°.
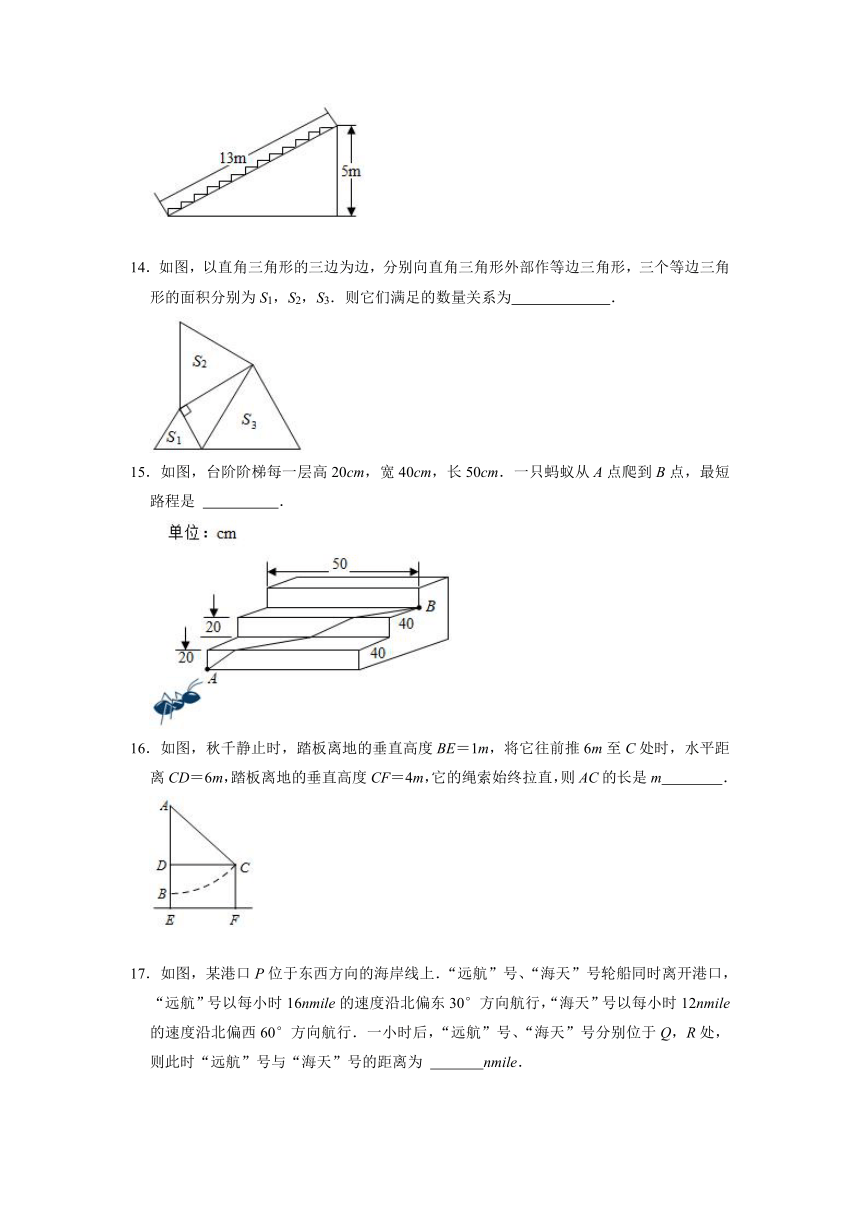
13.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
m.
14.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为
.
15.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是
.
16.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m
.
17.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,“远航”号以每小时16nmile的速度沿北偏东30°方向航行,“海天”号以每小时12nmile的速度沿北偏西60°方向航行.一小时后,“远航”号、“海天”号分别位于Q,R处,则此时“远航”号与“海天”号的距离为
nmile.
18.如图,小磊将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,测得MA=a,梯子的底端P保持不动,将梯子的顶端靠在对面墙上,此时∠MPN=90°,梯子的顶端距离地面的垂直距离记作NB,测得NB=b,求A、B之间的距离.
19.勾股定理是毕达哥拉斯定理的中国称谓,它揭示了直角三角形三边的数量关系:直角三角形两直角边的平方和等于斜边的平方,中国是发现、研究和运用勾股定理最古老的国家之一,我国古代称直角三角形的直角边为“勾”或“股”,斜边为“弦”,因而将这条定理称为勾股定理.请你从以下图形中,任意选择一个来证明这个定理.
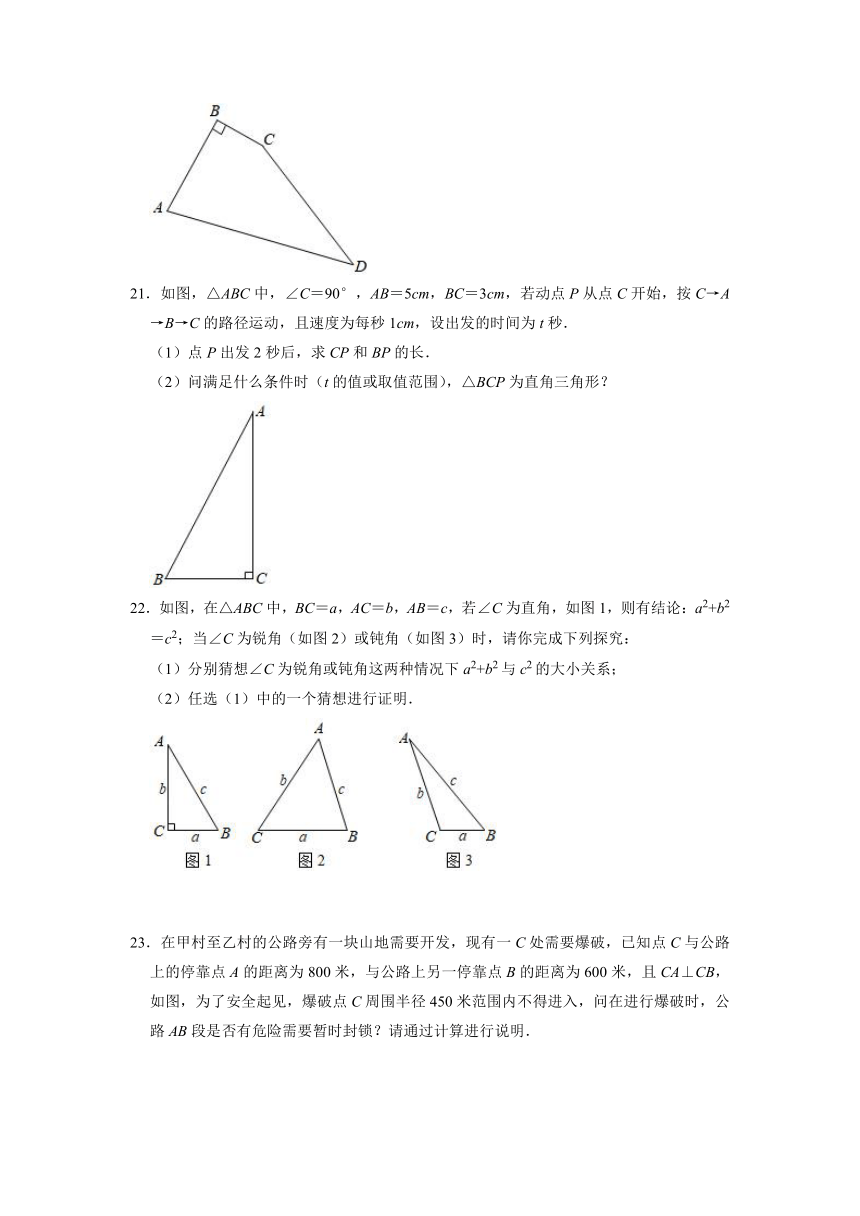
20.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
21.如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)点P出发2秒后,求CP和BP的长.
(2)问满足什么条件时(t的值或取值范围),△BCP为直角三角形?
22.如图,在△ABC中,BC=a,AC=b,AB=c,若∠C为直角,如图1,则有结论:a2+b2=c2;当∠C为锐角(如图2)或钝角(如图3)时,请你完成下列探究:
(1)分别猜想∠C为锐角或钝角这两种情况下a2+b2与c2的大小关系;
(2)任选(1)中的一个猜想进行证明.
23.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.
24.课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股数的勾都是奇数,且从3起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、
、
;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?聪明的小明发现每组第二个数有这样的规律4=,12=,24=…,于是他很快表示了第二数为,则用含a的代数式表示第三个数为
;
(3)用所学知识加以说明.
参考答案
1.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
2.解:A、52+122=132,且都是正整数,是勾股数,故此选项符合题意;
B、不是勾股数,故此选项不合题意;
C、22+22≠32,不是勾股数,故此选项不合题意;
D、,,不是正整数,不是勾股数,故此选项不合题意;
故选:A.
3.解:A、62+82≠112,不符合勾股定理的逆定理,不是直角三角形,故符合题意;
B、52+122=132,符合勾股定理的逆定理,是直角三角形,故不符合题意;
C、72+242=252,符合勾股定理的逆定理,是直角三角形,故不符合题意;
D、32+42=52,符合勾股定理的逆定理,是直角三角形,故不符合题意;
故选:A.
4.解:A、72+242=252,能判断△ABC是直角三角形,不符合题意;
B、∠B﹣∠C=∠A,∴∠B=90°,能判断△ABC是直角三角形,不符合题意;
C、∠A:∠B:∠C=6:8:10,∠C=,不能判断△ABC是直角三角形,符合题意;
D、a2=(b+c)(b﹣c),∴a2+c2=b2,能判断△ABC是直角三角形,不符合题意;
故选:C.
5.解:∵AB2=132=169,
BC2+AC2=52+122=169,
∴AB2=BC2+AC2,
即△ABC是直角三角形,
∴S△ABC=BC×AC
=×5×12
=30,
故选:B.
6.解:当b为直角边时,c2=a2+b2=25,
∴c=5,
当b为斜边时,c2=b2﹣a2=7,
∴c=,
综上所述,c的值是5或,
故选:C.
7.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
8.解:连接DE,
∵AD=AB,AE⊥BD,
∴AE是BD的垂直平分线,
∴DE=BE,
∴∠EBD=∠EDB,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADE=∠ABE=90°,
在△ABC中,∠ABC=90°,
由勾股定理得:AC=5,
∴CD=AC﹣AD=5﹣3=2,
设BE=x,则CE=4﹣x,
在Rt△CDE中,由勾股定理得:
x2+22=(4﹣x)2,
解得x=,
∴BE=.
故选:B.
9.解:∵OA12=1,
∴由勾股定理可得OA22=2,
OA32=3,
…,
∴OAn2=n,
∴OA82=8.
故选:D.
10.解:设MF与AB交于点K,
∵正方形EFGH的面积为1,
∴EF=FG=EH=HG=1,
又∵正方形MNPQ的面积为49,
∴MN=NP=PQ=MQ=7,
设所有全等三角形的较长直角边为a,另一直角边为b,斜边为c,
则,
解得:a=4,b=3,
∴斜边c==5,
∴MO=,
又∵S△ABF==,
即=,
∴FK=,
∵△ABM是由△ABF沿边AB翻折所得,
∴△ABM≌△ABF,
∴MK=KF=,
∴MF=2KF=,
∴OF=MO﹣MF==,
故选:B.
11.解:在△ABC中,∠C=90°,a=5,b=12,
∴c-13,
故答案为:13.
12.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
13.解:由勾股定理得:
楼梯的水平宽度=12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
14.解:设AC=a,BC=b,AB=c,
∵△ABC是直角三角形,
∴a2+b2=c2,
∴S1+S2=S3,
故答案是:S1+S2=S3.
15.解:如图所示,
∵它的每一级的长宽高为20cm,宽40cm,长50cm,
∴AB=130(cm).
答:蚂蚁沿着台阶面爬行到点B的最短路程是130cm.
故答案为:130cm.
16.解:设秋千绳索AB的长度为xm,
由题意可得AC=AB=xm,
四边形DCFE为矩形,BE=1m,DC=6m,CF=4m,DE=CF=4m,
∴DB=DE﹣BE=3m,AD=AB﹣BD=(x﹣3)m,
在Rt△ADC中,AD2+DC2=AC2,
即(x﹣3)2+62=x2,
解得x=7.5,
即AC的长度为7.5m,
故答案为:7.5.
17.解:由题意可得,∠RPQ=60°+30°=90°,
PQ=16×1=16,PR=12×1=12,
∴RQ=20nmile,
故答案为:20.
18.解:∵∠MPN=90°,
∴∠APM+∠BPN=90°,
∵∠APM+∠AMP=90°,
∴∠AMP=∠BPN.
在△AMP与△BPN中,
,
∴△AMP≌△BPN(AAS),
∴MA=PB=a,PA=NB=b,
∴AB=PA+PB=a+b.
19.证明:方法一:由(1)图可知:S正方形ABCD=(a+b)2=a2+b2+2ab,
又∵S正方形ABCD=,
∴a2+b2+2ab=2ab+c2,
∴a2+b2=c2,
方法二:由(2)图可知:S正方形ABCD=c2,
又∵S正方形ABCD==2ab+a2+b2﹣2ab=a2+b2,
∴a2+b2=c2,
方法三:由(3)图可知:S梯形ABCD==+ab,
又∵s梯形ABCD=,
∴,
∴a2+b2=c2.
20.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC?CD+AB?BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
21.(1)∵∠C=90°,AB=5cm,BC=3cm,
∴AC=4cm,
∵动点P从点C开始以每秒1cm的速度运动,
∴出发2秒后CP=1×2=2(cm),
∵∠C=90°,
∴BP==(cm),
(2)设运动时间为t秒,
∵AC=4cm,动点P从点C开始按C→A→B→C的路径运动,且速度为每秒1cm,
∴当P在AC上运动时,△BCP为直角三角形,
∴0<t≤4,
如图,当P在AB上时,CP⊥AB时,△BCP为直角三角形,
∵AB?CP=AC?BC,
∴×5CP=×3×4,
∴CP=cm,
∴AP=(cm),
∴AC+AP=4+=(cm),
∴t=÷1=(s),
综上所述,当0<t≤4或
t=时,△BCP为直角三角形.
22.解:(1)猜想:若∠C为锐角时,a2+b2>c2,若∠C为钝角时,a2+b2<c2;
(2)当∠C为锐角时,a2+b2>c2,证明如下:
如图,过点A作AD⊥CB于点D,设CD=x,则BD=a﹣x,
在直角三角形ACD中,AD2=b2﹣x2,
在直角三角形ABD中,AD2=c2﹣(a﹣x)2,
∴b2﹣x2=c2﹣(a﹣x)2,即a2+b2=c2+2ax,
∵a>0,x>0,
∴a2+b2>c2,
当∠C为钝角时,a2+b2<c2,证明如下:
如图,过点A作BC的垂线交BC的延长线于点M,CM=y,则BM=a+y,
在直角三角形ACM中,AM2=b2﹣y2,
在直角三角形ABM中,AM2=c2﹣(a+y)2,
∴b2﹣y2=c2﹣(a+y)2,即a2+b2=c2﹣2ay,
∵a>0,y>0,
∴a2+b2<c2.
23.解:公路AB不需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
∵CA⊥CB,
∴∠ACB=90°,
因为BC=800米,AC=600米,
所以,根据勾股定理有AB=1000(米).
因为S△ABC=AB?CD=BC?AC
所以CD===480(米).
由于400米<480米,故没有危险,
因此AB段公路不需要暂时封锁.
24.解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,
∴11,60,61;
故答案为:60,61;
(2)第一个数用字母a(a为奇数,且a≥3)表示,第二数为,
则用含a的代数式表示第三个数为,
故答案为:;
(3)∵a2+()2=,
()2=,
∴a2+()2=()2
又∵a为奇数,且a≥3,
∴由a,,三个数组成的数是勾股数
1.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5
B.7
C.13
D.15
2.下列各组数中是勾股数的是( )
A.5,12,13
B.7,23,25
C.2,2,3
D.
3.以下列各组数的长度围成的三角形中,不是直角三角形的一组是( )
A.6,8,11
B.5,12,13
C.25,7,24
D.3,4,5
4.下列条件中不能判断△ABC是直角三角形的是( )
A.a:b:c=7:24:25
B.∠B﹣∠C=∠A
C.∠A:∠B:∠C=6:8:10
D.a2=(b+c)(b﹣c)
5.如图,一块三角形木板,测得AB=13,BC=5,AC=12,则三角形木板ABC的面积为( )
A.60
B.30
C.65
D.不能确定
6.直角三角形的边长分别为a,b,c,若a2=9,b2=16,那么c2的值是( )
A.25
B.49
C.25或7
D.25或49
7.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2
B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2
D.x2+92=(20﹣x)2
8.如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点D在边AC上,AD=AB,AE⊥BD,垂足为点F,交BC于点E,则BE的长为( )
A.2
B.
C.
D.
9.图1是第七届国际数学教育大会(ICME﹣7)会徽图案,它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如果图2中的OA1=A1A2=A2A3=?=A7A8=1,那么OA82为( )
A.10
B.16
C.9
D.8
10.如图,在“赵爽弦图”中,正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成的,若把四个直角三角形分别沿斜边向外翻折,可得正方形MNPQ,连接MF并延长交NP于点O,若正方形MNPQ的面积为49,正方形EFGH的面积为1,则OF的长为( )
A.
B.
C.
D.
11.在△ABC中,∠C=90°,若a=5,b=12,则c=
.
12.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k=
时,∠C=90°.
13.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
m.
14.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为
.
15.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是
.
16.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m
.
17.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,“远航”号以每小时16nmile的速度沿北偏东30°方向航行,“海天”号以每小时12nmile的速度沿北偏西60°方向航行.一小时后,“远航”号、“海天”号分别位于Q,R处,则此时“远航”号与“海天”号的距离为
nmile.
18.如图,小磊将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,测得MA=a,梯子的底端P保持不动,将梯子的顶端靠在对面墙上,此时∠MPN=90°,梯子的顶端距离地面的垂直距离记作NB,测得NB=b,求A、B之间的距离.
19.勾股定理是毕达哥拉斯定理的中国称谓,它揭示了直角三角形三边的数量关系:直角三角形两直角边的平方和等于斜边的平方,中国是发现、研究和运用勾股定理最古老的国家之一,我国古代称直角三角形的直角边为“勾”或“股”,斜边为“弦”,因而将这条定理称为勾股定理.请你从以下图形中,任意选择一个来证明这个定理.
20.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
21.如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)点P出发2秒后,求CP和BP的长.
(2)问满足什么条件时(t的值或取值范围),△BCP为直角三角形?
22.如图,在△ABC中,BC=a,AC=b,AB=c,若∠C为直角,如图1,则有结论:a2+b2=c2;当∠C为锐角(如图2)或钝角(如图3)时,请你完成下列探究:
(1)分别猜想∠C为锐角或钝角这两种情况下a2+b2与c2的大小关系;
(2)任选(1)中的一个猜想进行证明.
23.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.
24.课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股数的勾都是奇数,且从3起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、
、
;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?聪明的小明发现每组第二个数有这样的规律4=,12=,24=…,于是他很快表示了第二数为,则用含a的代数式表示第三个数为
;
(3)用所学知识加以说明.
参考答案
1.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
2.解:A、52+122=132,且都是正整数,是勾股数,故此选项符合题意;
B、不是勾股数,故此选项不合题意;
C、22+22≠32,不是勾股数,故此选项不合题意;
D、,,不是正整数,不是勾股数,故此选项不合题意;
故选:A.
3.解:A、62+82≠112,不符合勾股定理的逆定理,不是直角三角形,故符合题意;
B、52+122=132,符合勾股定理的逆定理,是直角三角形,故不符合题意;
C、72+242=252,符合勾股定理的逆定理,是直角三角形,故不符合题意;
D、32+42=52,符合勾股定理的逆定理,是直角三角形,故不符合题意;
故选:A.
4.解:A、72+242=252,能判断△ABC是直角三角形,不符合题意;
B、∠B﹣∠C=∠A,∴∠B=90°,能判断△ABC是直角三角形,不符合题意;
C、∠A:∠B:∠C=6:8:10,∠C=,不能判断△ABC是直角三角形,符合题意;
D、a2=(b+c)(b﹣c),∴a2+c2=b2,能判断△ABC是直角三角形,不符合题意;
故选:C.
5.解:∵AB2=132=169,
BC2+AC2=52+122=169,
∴AB2=BC2+AC2,
即△ABC是直角三角形,
∴S△ABC=BC×AC
=×5×12
=30,
故选:B.
6.解:当b为直角边时,c2=a2+b2=25,
∴c=5,
当b为斜边时,c2=b2﹣a2=7,
∴c=,
综上所述,c的值是5或,
故选:C.
7.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
8.解:连接DE,
∵AD=AB,AE⊥BD,
∴AE是BD的垂直平分线,
∴DE=BE,
∴∠EBD=∠EDB,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADE=∠ABE=90°,
在△ABC中,∠ABC=90°,
由勾股定理得:AC=5,
∴CD=AC﹣AD=5﹣3=2,
设BE=x,则CE=4﹣x,
在Rt△CDE中,由勾股定理得:
x2+22=(4﹣x)2,
解得x=,
∴BE=.
故选:B.
9.解:∵OA12=1,
∴由勾股定理可得OA22=2,
OA32=3,
…,
∴OAn2=n,
∴OA82=8.
故选:D.
10.解:设MF与AB交于点K,
∵正方形EFGH的面积为1,
∴EF=FG=EH=HG=1,
又∵正方形MNPQ的面积为49,
∴MN=NP=PQ=MQ=7,
设所有全等三角形的较长直角边为a,另一直角边为b,斜边为c,
则,
解得:a=4,b=3,
∴斜边c==5,
∴MO=,
又∵S△ABF==,
即=,
∴FK=,
∵△ABM是由△ABF沿边AB翻折所得,
∴△ABM≌△ABF,
∴MK=KF=,
∴MF=2KF=,
∴OF=MO﹣MF==,
故选:B.
11.解:在△ABC中,∠C=90°,a=5,b=12,
∴c-13,
故答案为:13.
12.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
13.解:由勾股定理得:
楼梯的水平宽度=12,
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
∴地毯的长度至少是12+5=17(米).
故答案为:17.
14.解:设AC=a,BC=b,AB=c,
∵△ABC是直角三角形,
∴a2+b2=c2,
∴S1+S2=S3,
故答案是:S1+S2=S3.
15.解:如图所示,
∵它的每一级的长宽高为20cm,宽40cm,长50cm,
∴AB=130(cm).
答:蚂蚁沿着台阶面爬行到点B的最短路程是130cm.
故答案为:130cm.
16.解:设秋千绳索AB的长度为xm,
由题意可得AC=AB=xm,
四边形DCFE为矩形,BE=1m,DC=6m,CF=4m,DE=CF=4m,
∴DB=DE﹣BE=3m,AD=AB﹣BD=(x﹣3)m,
在Rt△ADC中,AD2+DC2=AC2,
即(x﹣3)2+62=x2,
解得x=7.5,
即AC的长度为7.5m,
故答案为:7.5.
17.解:由题意可得,∠RPQ=60°+30°=90°,
PQ=16×1=16,PR=12×1=12,
∴RQ=20nmile,
故答案为:20.
18.解:∵∠MPN=90°,
∴∠APM+∠BPN=90°,
∵∠APM+∠AMP=90°,
∴∠AMP=∠BPN.
在△AMP与△BPN中,
,
∴△AMP≌△BPN(AAS),
∴MA=PB=a,PA=NB=b,
∴AB=PA+PB=a+b.
19.证明:方法一:由(1)图可知:S正方形ABCD=(a+b)2=a2+b2+2ab,
又∵S正方形ABCD=,
∴a2+b2+2ab=2ab+c2,
∴a2+b2=c2,
方法二:由(2)图可知:S正方形ABCD=c2,
又∵S正方形ABCD==2ab+a2+b2﹣2ab=a2+b2,
∴a2+b2=c2,
方法三:由(3)图可知:S梯形ABCD==+ab,
又∵s梯形ABCD=,
∴,
∴a2+b2=c2.
20.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC?CD+AB?BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
21.(1)∵∠C=90°,AB=5cm,BC=3cm,
∴AC=4cm,
∵动点P从点C开始以每秒1cm的速度运动,
∴出发2秒后CP=1×2=2(cm),
∵∠C=90°,
∴BP==(cm),
(2)设运动时间为t秒,
∵AC=4cm,动点P从点C开始按C→A→B→C的路径运动,且速度为每秒1cm,
∴当P在AC上运动时,△BCP为直角三角形,
∴0<t≤4,
如图,当P在AB上时,CP⊥AB时,△BCP为直角三角形,
∵AB?CP=AC?BC,
∴×5CP=×3×4,
∴CP=cm,
∴AP=(cm),
∴AC+AP=4+=(cm),
∴t=÷1=(s),
综上所述,当0<t≤4或
t=时,△BCP为直角三角形.
22.解:(1)猜想:若∠C为锐角时,a2+b2>c2,若∠C为钝角时,a2+b2<c2;
(2)当∠C为锐角时,a2+b2>c2,证明如下:
如图,过点A作AD⊥CB于点D,设CD=x,则BD=a﹣x,
在直角三角形ACD中,AD2=b2﹣x2,
在直角三角形ABD中,AD2=c2﹣(a﹣x)2,
∴b2﹣x2=c2﹣(a﹣x)2,即a2+b2=c2+2ax,
∵a>0,x>0,
∴a2+b2>c2,
当∠C为钝角时,a2+b2<c2,证明如下:
如图,过点A作BC的垂线交BC的延长线于点M,CM=y,则BM=a+y,
在直角三角形ACM中,AM2=b2﹣y2,
在直角三角形ABM中,AM2=c2﹣(a+y)2,
∴b2﹣y2=c2﹣(a+y)2,即a2+b2=c2﹣2ay,
∵a>0,y>0,
∴a2+b2<c2.
23.解:公路AB不需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
∵CA⊥CB,
∴∠ACB=90°,
因为BC=800米,AC=600米,
所以,根据勾股定理有AB=1000(米).
因为S△ABC=AB?CD=BC?AC
所以CD===480(米).
由于400米<480米,故没有危险,
因此AB段公路不需要暂时封锁.
24.解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,
∴11,60,61;
故答案为:60,61;
(2)第一个数用字母a(a为奇数,且a≥3)表示,第二数为,
则用含a的代数式表示第三个数为,
故答案为:;
(3)∵a2+()2=,
()2=,
∴a2+()2=()2
又∵a为奇数,且a≥3,
∴由a,,三个数组成的数是勾股数
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
