2021—2022学年北师大版数学九年级上册1.2 矩形的性质与判定(第3课时) 课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级上册1.2 矩形的性质与判定(第3课时) 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 06:46:53 | ||
图片预览





文档简介
(共17张PPT)
1.2
矩形的性质与判定(第3课时)
学习目标
1.
能够运用综合法和严密的数学语言证明矩形的性质和判定定理以及其他相关结论;
2.
学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.
让学生感受合作学习的成功
新课导入
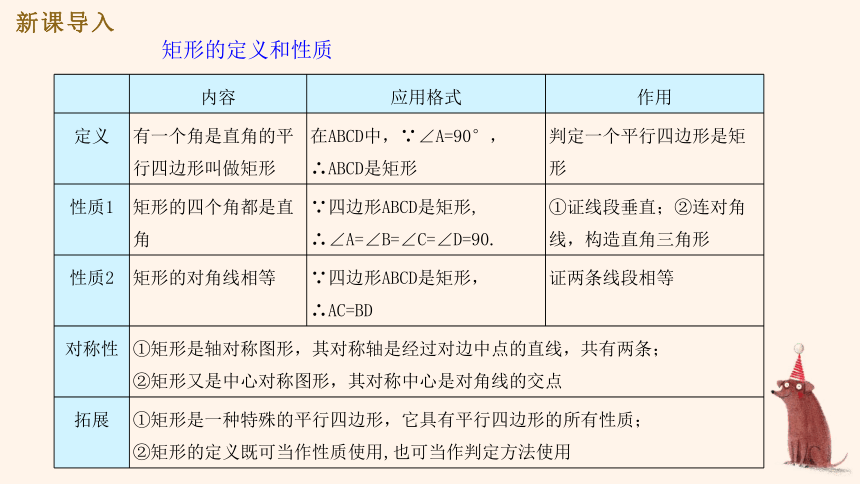
?矩形的定义和性质
内容
应用格式
作用
定义
有一个角是直角的平行四边形叫做矩形
在ABCD中,∵∠A=90°,
∴ABCD是矩形
判定一个平行四边形是矩形
性质1
矩形的四个角都是直角
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90.
①证线段垂直;②连对角线,构造直角三角形
性质2
矩形的对角线相等
∵四边形ABCD是矩形,
∴AC=BD
证两条线段相等
对称性
①矩形是轴对称图形,其对称轴是经过对边中点的直线,共有两条;
②矩形又是中心对称图形,其对称中心是对角线的交点
拓展
①矩形是一种特殊的平行四边形,它具有平行四边形的所有性质;
②矩形的定义既可当作性质使用,也可当作判定方法使用
新课导入
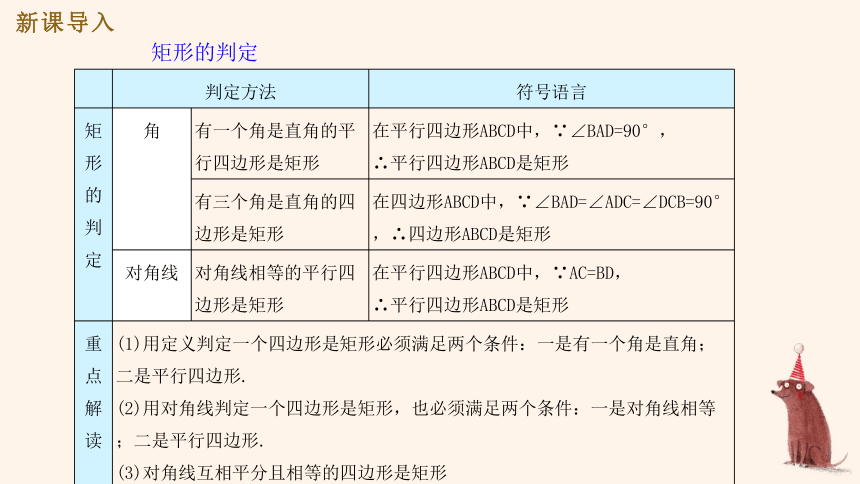
矩形的判定
判定方法
符号语言
矩形的判定
角
有一个角是直角的平行四边形是矩形
在平行四边形ABCD中,∵∠BAD=90°,
∴平行四边形ABCD是矩形
有三个角是直角的四边形是矩形
在四边形ABCD中,∵∠BAD=∠ADC=∠DCB=90°,∴四边形ABCD是矩形
对角线
对角线相等的平行四边形是矩形
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形
重点
解读
(1)用定义判定一个四边形是矩形必须满足两个条件:一是有一个角是直角;二是平行四边形.
(2)用对角线判定一个四边形是矩形,也必须满足两个条件:一是对角线相等;二是平行四边形.
(3)对角线互相平分且相等的四边形是矩形
典例精析
例1、如图是四根木棒搭成的平行四边形框架,AB=8
cm,AD=6
cm,使AB固定,转动AD,当∠DAB=_________时,ABCD的面积最大,此时ABCD是_________形,面积为__________.
解析 当AB、CD间的距离最大时,?ABCD的面积最大,此时它是矩形,
即∠DAB=90°,面积为48
cm2.
A
B
C
D
90°
矩
48
cm2
典例精析
例2、如图,已知在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.
求证:EF=AD.
证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形.
又∵∠BAC=90°,
∴平行四边形AEDF是矩形.
∴EF=AD.
典例精析
例3、在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为多少?
解:设AC与BD交于点O.
连接OP,∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,OA=OC,OB=OD,
∴OA=OD=
BD,S△AOD=S△AOB,
∵AB=3,AD=4,
∴S矩形ABCD=3×4=12,BD==5,
∴S△AOD=
S矩形ABCD=3,OA=OC=
?,
∵S△AOD=S△AOP+S△DOP=
OA·PE+
OD·PF=
××PE+
×
×PF=
(PE+PF)=3,
∴PE+PF=
.
O
典例精析
例4、如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4
cm,BC=6
cm,AE=CG=3
cm,BF=DH=4
cm,四边形AEPH的面积为5
cm2,则四边形PFCG的面积为多少?
解:连接AP,CP,
设△AHP中AH边上的高为x
cm,△AEP中AE边上的高为y
cm,则△CFP中CF边上的高为(4-x)cm,△CGP中CG边上的高为(6-y)cm.
由已知得AH=CF=2
cm,又AE=CG=3
cm,
∴S四边形AEPH=S△AHP+S△AEP=AH·x·?+AE·y·=2x·+3y·=5
cm2,
∴2x+3y=10,
∴S四边形PFCG=S△CFP+S△CGP=CF·(4-x)+CG·(6-y)
=2(4-x)·?+3(6-y)·?=(26-2x-3y)·?=(26-10)×=8(cm2).
典例精析
例5、在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设∠BCA的平分线交MN于点E,△BCA的外角∠ACD的平分线交MN于点F.
(1)证明:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?简要说明理由.
(1)证明:∵MN∥BC,
∴∠CEO=∠ECB,∠CFO=∠FCD.
∵CE,CF分别是∠BCA,∠ACD的平分线,
∴∠ECO=∠ECB,∠FCO=∠FCD,
∴∠CEO=∠ECO,∠CFO=∠FCO,
∴EO=OC,FO=OC,∴EO=FO.
典例精析
例5、在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设∠BCA的平分线交MN于点E,△BCA的外角∠ACD的平分线交MN于点F.
(1)证明:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?简要说明理由.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:由(1)知EO=FO.
又∵AO=CO,
∴四边形AECF是平行四边形.
∵OE=OC,∴EF=AC,
∴平行四边形AECF是矩形.
随堂练习
1.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=
( )
A.5 ???
?B.4 ????
C.3.5 ?
???D.3
B
A
B
C
D
O
随堂练习
2.在Rt△ABC中,∠C=90°,∠B=30°,最短边长为5
cm,则最长边上的中线长是?( )
A.5
cm
B.15
cm
C.10
cm
D.2.5
cm
A
随堂练习
3.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12厘米,EF=16厘米,则边AD的长是
( )
A.12厘米 ????
B.16厘米 ????
C.20厘米 ???
?D.28厘米
C
随堂练习
4.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( )
A.3 ????
B.
????
C.5 ??
??D.
?
B
随堂练习
5、工人师傅做铝合金窗框分下面三个步骤进行:
(1)如图①,先截出两对符合规格的铝合金窗料,使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是__________形,根据
的数学原理是____________________;
(3)如图③,将直角尺靠紧窗框的一个角,调整窗框的边框,当直角尺
的两条直角边与窗框无缝隙时说明窗框合格,这时窗框是________形,
根据的数学原理是_______________________.
A
B
C
D
E
F
G
H
①
②
③
平行四边
两组对边分别相等的四边形是平行四边形
矩
有一个角是直角的平行四边形是矩形
随堂练习
6、如图,已知菱形ABCD的对角线AC,BD相交于点O,点E是菱形外一点,且DE∥AC,CE∥BD,连接OE.求证:OE=CD.
证明:∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴ODEC是矩形,
∴OE=CD.
课堂小结
矩形的性质和判定的综合应用
运用矩形的性质可以证明线段相等或线段之间的倍分关系,以及直线的位置关系、角的等量关系,常常与直角三角形的有关知识综合运用.
1.2
矩形的性质与判定(第3课时)
学习目标
1.
能够运用综合法和严密的数学语言证明矩形的性质和判定定理以及其他相关结论;
2.
学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.
让学生感受合作学习的成功
新课导入
?矩形的定义和性质
内容
应用格式
作用
定义
有一个角是直角的平行四边形叫做矩形
在ABCD中,∵∠A=90°,
∴ABCD是矩形
判定一个平行四边形是矩形
性质1
矩形的四个角都是直角
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90.
①证线段垂直;②连对角线,构造直角三角形
性质2
矩形的对角线相等
∵四边形ABCD是矩形,
∴AC=BD
证两条线段相等
对称性
①矩形是轴对称图形,其对称轴是经过对边中点的直线,共有两条;
②矩形又是中心对称图形,其对称中心是对角线的交点
拓展
①矩形是一种特殊的平行四边形,它具有平行四边形的所有性质;
②矩形的定义既可当作性质使用,也可当作判定方法使用
新课导入
矩形的判定
判定方法
符号语言
矩形的判定
角
有一个角是直角的平行四边形是矩形
在平行四边形ABCD中,∵∠BAD=90°,
∴平行四边形ABCD是矩形
有三个角是直角的四边形是矩形
在四边形ABCD中,∵∠BAD=∠ADC=∠DCB=90°,∴四边形ABCD是矩形
对角线
对角线相等的平行四边形是矩形
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形
重点
解读
(1)用定义判定一个四边形是矩形必须满足两个条件:一是有一个角是直角;二是平行四边形.
(2)用对角线判定一个四边形是矩形,也必须满足两个条件:一是对角线相等;二是平行四边形.
(3)对角线互相平分且相等的四边形是矩形
典例精析
例1、如图是四根木棒搭成的平行四边形框架,AB=8
cm,AD=6
cm,使AB固定,转动AD,当∠DAB=_________时,ABCD的面积最大,此时ABCD是_________形,面积为__________.
解析 当AB、CD间的距离最大时,?ABCD的面积最大,此时它是矩形,
即∠DAB=90°,面积为48
cm2.
A
B
C
D
90°
矩
48
cm2
典例精析
例2、如图,已知在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.
求证:EF=AD.
证明:∵DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形.
又∵∠BAC=90°,
∴平行四边形AEDF是矩形.
∴EF=AD.
典例精析
例3、在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为多少?
解:设AC与BD交于点O.
连接OP,∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,OA=OC,OB=OD,
∴OA=OD=
BD,S△AOD=S△AOB,
∵AB=3,AD=4,
∴S矩形ABCD=3×4=12,BD==5,
∴S△AOD=
S矩形ABCD=3,OA=OC=
?,
∵S△AOD=S△AOP+S△DOP=
OA·PE+
OD·PF=
××PE+
×
×PF=
(PE+PF)=3,
∴PE+PF=
.
O
典例精析
例4、如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4
cm,BC=6
cm,AE=CG=3
cm,BF=DH=4
cm,四边形AEPH的面积为5
cm2,则四边形PFCG的面积为多少?
解:连接AP,CP,
设△AHP中AH边上的高为x
cm,△AEP中AE边上的高为y
cm,则△CFP中CF边上的高为(4-x)cm,△CGP中CG边上的高为(6-y)cm.
由已知得AH=CF=2
cm,又AE=CG=3
cm,
∴S四边形AEPH=S△AHP+S△AEP=AH·x·?+AE·y·=2x·+3y·=5
cm2,
∴2x+3y=10,
∴S四边形PFCG=S△CFP+S△CGP=CF·(4-x)+CG·(6-y)
=2(4-x)·?+3(6-y)·?=(26-2x-3y)·?=(26-10)×=8(cm2).
典例精析
例5、在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设∠BCA的平分线交MN于点E,△BCA的外角∠ACD的平分线交MN于点F.
(1)证明:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?简要说明理由.
(1)证明:∵MN∥BC,
∴∠CEO=∠ECB,∠CFO=∠FCD.
∵CE,CF分别是∠BCA,∠ACD的平分线,
∴∠ECO=∠ECB,∠FCO=∠FCD,
∴∠CEO=∠ECO,∠CFO=∠FCO,
∴EO=OC,FO=OC,∴EO=FO.
典例精析
例5、在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设∠BCA的平分线交MN于点E,△BCA的外角∠ACD的平分线交MN于点F.
(1)证明:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?简要说明理由.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:由(1)知EO=FO.
又∵AO=CO,
∴四边形AECF是平行四边形.
∵OE=OC,∴EF=AC,
∴平行四边形AECF是矩形.
随堂练习
1.如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=4,则OC=
( )
A.5 ???
?B.4 ????
C.3.5 ?
???D.3
B
A
B
C
D
O
随堂练习
2.在Rt△ABC中,∠C=90°,∠B=30°,最短边长为5
cm,则最长边上的中线长是?( )
A.5
cm
B.15
cm
C.10
cm
D.2.5
cm
A
随堂练习
3.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12厘米,EF=16厘米,则边AD的长是
( )
A.12厘米 ????
B.16厘米 ????
C.20厘米 ???
?D.28厘米
C
随堂练习
4.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( )
A.3 ????
B.
????
C.5 ??
??D.
?
B
随堂练习
5、工人师傅做铝合金窗框分下面三个步骤进行:
(1)如图①,先截出两对符合规格的铝合金窗料,使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是__________形,根据
的数学原理是____________________;
(3)如图③,将直角尺靠紧窗框的一个角,调整窗框的边框,当直角尺
的两条直角边与窗框无缝隙时说明窗框合格,这时窗框是________形,
根据的数学原理是_______________________.
A
B
C
D
E
F
G
H
①
②
③
平行四边
两组对边分别相等的四边形是平行四边形
矩
有一个角是直角的平行四边形是矩形
随堂练习
6、如图,已知菱形ABCD的对角线AC,BD相交于点O,点E是菱形外一点,且DE∥AC,CE∥BD,连接OE.求证:OE=CD.
证明:∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴ODEC是矩形,
∴OE=CD.
课堂小结
矩形的性质和判定的综合应用
运用矩形的性质可以证明线段相等或线段之间的倍分关系,以及直线的位置关系、角的等量关系,常常与直角三角形的有关知识综合运用.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
