2021--2022学年沪科版七年级数学上册 _1.5 有理数的乘除 第二课时 课件(word版含答案)
文档属性
| 名称 | 2021--2022学年沪科版七年级数学上册 _1.5 有理数的乘除 第二课时 课件(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 07:43:30 | ||
图片预览






文档简介
(共16张PPT)
1.5
有理数的乘除
沪科版七年级数学(上)
第二课时
多个有理数相乘
知识回顾
有理数乘法的法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
倒
数
如果两个数a,b满足ab=1,那么a,b互为倒数
倒数的性质:
(1)如果a,b互为倒数,那么ab=1;
(2)0没有倒数(因为0与任何数相乘都不为1)
(3)正数的倒数是正数,负数的倒数是负数
(4)倒数等于它本身的数是±1
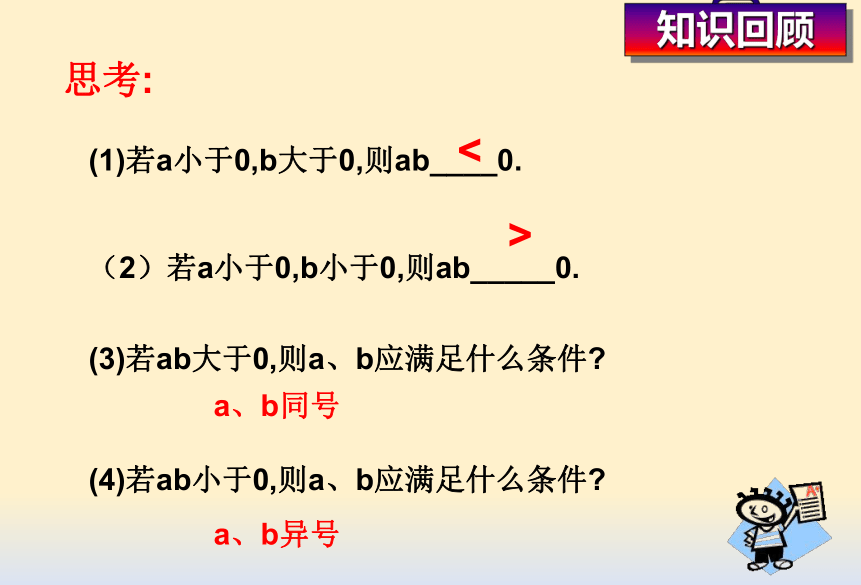
思考:
若a小于0,b大于0,则ab____0.
(2)若a小于0,b小于0,则ab_____0.
(3)若ab大于0,则a、b应满足什么条件?
(4)若ab小于0,则a、b应满足什么条件?
>
<
a、b同号
a、b异号
知识回顾
计算:
(1)(-6)×(+5);
练一练
解:(1)(-6)×(+5)=-6×5=-30.
你做对了吗?
计算下面各式
(1)4×5×(-5)×6
(2)
4×3×(-4)×2×(-3)
(3)
(-3)×3×7×(-6)×(-2)
(4)
(-4)×5×(-2)×0×(-7)
(5)
4×0×6×7
新知探究
积的符号与各因数的符号之间有什么关系?
解:(1)4×5×(-5)×6
=20×(-5)×6
=-100
×6
=-600
(2)
4×3×(-4)×2×(-3)
=12×(-4)×2×(-3)
=-48×2×(-3)
=-96
×(-3)
=+288
(3)
(-3)×3×7×(-6)×(-2)
=
-9×7×(-6)×(-2)
=-63×(-6)×(-2)
=+378×(-2)
=-756
(4)
(-4)×5×(-2)×0×(-7)
=-20
×(-2)×0×(-7)
=40×0×(-7)
=
0×(-7)
=0
(5)
4×0×6×7
=
0×6×7
=0×7
=0
我发现
多个有理数连乘,积的符号规律是什么?
新知探究
讨
论:
(3)几个数相乘,如果其中有因数为0,那么积等于0.
(1)负因数的个数为偶数,结果为正数.
(2)负因数的个数为奇数,结果为负数.
判断下列积的符号
正
负
负
正
0
负
新知验证
归纳:
当负因数的个数为奇数时,积为____;
当负因数的个数为偶数时,积为____。
结论1:几个不等于0的数相乘,积的符号由______________决定;
结论2:有一个因数为0,则积为____;
负因数的个数
负
正
0
几个不是0的数相乘时,积的符号由负因数的个数决定:负因数的个数是偶数时,积是正数,负因数的个数为奇数时,积是负数.
几个数相乘,如果其中有因数为0,积等于0.
多个有理数相乘法则
法则总结
例1、计算:
例题精讲
(3)(-4)×5×(-0.25);
先说一说多个有理数相乘计算步骤
1、是否有因数0
2、确定积的符号,奇负偶正
3、把绝对值相乘
解:
(3)
(-4)×5×(-0.25)
=
[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=5;
计算:
(1)(-5)×(-4)×(-2)×(-2);
(2)
(3)
课堂练习
1.若a、b、c为有理数,且│a+1│+│b+2│
+│c+3│=0.求(a-1)×(b+2)×(c-3)
2.已知x、y为有理数,如果规定一种新运算※,定义x※y=xy+1.根据运算符号的意义完成下列各题.
(1)2※4
(2)求1※4※0
(3)(-5)※(-3)
※(-2)
(4)3
※
=13,你能求出
的值吗
?
a
a
提升练习
几个有理数相乘,因数都不为
0
时,
积的符号由
确定:
负因数的个数
奇数个为负,偶数个为正。
0
课堂小结
多个有理数相乘
有一因数为
0
时,积是
1.5
有理数的乘除
沪科版七年级数学(上)
第二课时
多个有理数相乘
知识回顾
有理数乘法的法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
倒
数
如果两个数a,b满足ab=1,那么a,b互为倒数
倒数的性质:
(1)如果a,b互为倒数,那么ab=1;
(2)0没有倒数(因为0与任何数相乘都不为1)
(3)正数的倒数是正数,负数的倒数是负数
(4)倒数等于它本身的数是±1
思考:
若a小于0,b大于0,则ab____0.
(2)若a小于0,b小于0,则ab_____0.
(3)若ab大于0,则a、b应满足什么条件?
(4)若ab小于0,则a、b应满足什么条件?
>
<
a、b同号
a、b异号
知识回顾
计算:
(1)(-6)×(+5);
练一练
解:(1)(-6)×(+5)=-6×5=-30.
你做对了吗?
计算下面各式
(1)4×5×(-5)×6
(2)
4×3×(-4)×2×(-3)
(3)
(-3)×3×7×(-6)×(-2)
(4)
(-4)×5×(-2)×0×(-7)
(5)
4×0×6×7
新知探究
积的符号与各因数的符号之间有什么关系?
解:(1)4×5×(-5)×6
=20×(-5)×6
=-100
×6
=-600
(2)
4×3×(-4)×2×(-3)
=12×(-4)×2×(-3)
=-48×2×(-3)
=-96
×(-3)
=+288
(3)
(-3)×3×7×(-6)×(-2)
=
-9×7×(-6)×(-2)
=-63×(-6)×(-2)
=+378×(-2)
=-756
(4)
(-4)×5×(-2)×0×(-7)
=-20
×(-2)×0×(-7)
=40×0×(-7)
=
0×(-7)
=0
(5)
4×0×6×7
=
0×6×7
=0×7
=0
我发现
多个有理数连乘,积的符号规律是什么?
新知探究
讨
论:
(3)几个数相乘,如果其中有因数为0,那么积等于0.
(1)负因数的个数为偶数,结果为正数.
(2)负因数的个数为奇数,结果为负数.
判断下列积的符号
正
负
负
正
0
负
新知验证
归纳:
当负因数的个数为奇数时,积为____;
当负因数的个数为偶数时,积为____。
结论1:几个不等于0的数相乘,积的符号由______________决定;
结论2:有一个因数为0,则积为____;
负因数的个数
负
正
0
几个不是0的数相乘时,积的符号由负因数的个数决定:负因数的个数是偶数时,积是正数,负因数的个数为奇数时,积是负数.
几个数相乘,如果其中有因数为0,积等于0.
多个有理数相乘法则
法则总结
例1、计算:
例题精讲
(3)(-4)×5×(-0.25);
先说一说多个有理数相乘计算步骤
1、是否有因数0
2、确定积的符号,奇负偶正
3、把绝对值相乘
解:
(3)
(-4)×5×(-0.25)
=
[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=5;
计算:
(1)(-5)×(-4)×(-2)×(-2);
(2)
(3)
课堂练习
1.若a、b、c为有理数,且│a+1│+│b+2│
+│c+3│=0.求(a-1)×(b+2)×(c-3)
2.已知x、y为有理数,如果规定一种新运算※,定义x※y=xy+1.根据运算符号的意义完成下列各题.
(1)2※4
(2)求1※4※0
(3)(-5)※(-3)
※(-2)
(4)3
※
=13,你能求出
的值吗
?
a
a
提升练习
几个有理数相乘,因数都不为
0
时,
积的符号由
确定:
负因数的个数
奇数个为负,偶数个为正。
0
课堂小结
多个有理数相乘
有一因数为
0
时,积是
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
