2021-2022学年华东师大版数学八年级上册12.3.2两数和(差)的平方课件(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册12.3.2两数和(差)的平方课件(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
标题
两数和的平方
标题
回顾与思考
公式的结构特征:
左边是
a2
?
b2;
两个二项式的乘积,
平方差公式
回顾
&
思考
?
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
两数的平方差.
2.计算下列各题:
=
=
=
m2+4m+4
完
全
平
方
公
式
一块边长为a米的正方形实验田,
做一做
图1—6
a
因需要将其边长增加
b
米。
形成四块实验田,以种植不同的新品种(如图1—6).
用不同的形式表示实验田的总面积,
并进行比较.
a
b
b
法一
直
接
求
总面积=
(a+b)
;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
你发现了什么?
探索:
2
公式:
完全平方公式
动脑筋
想一想
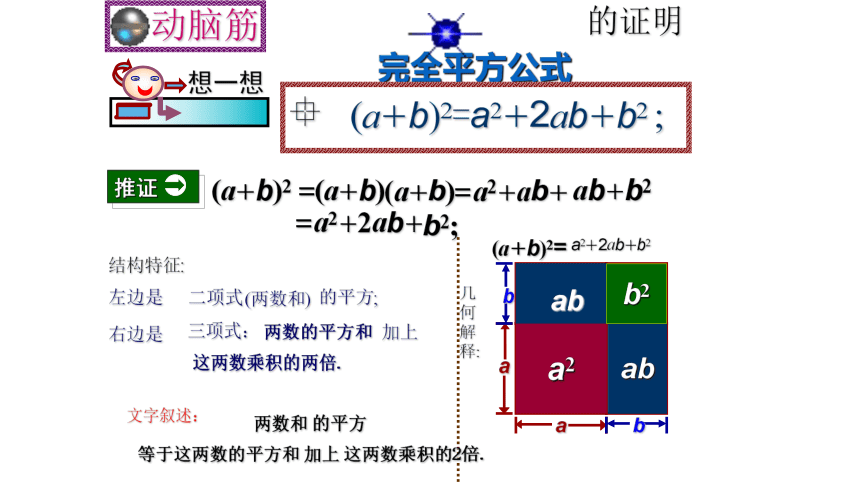
(a+b)2=a2+2ab+b2
;
(a+b)2
=
推证
?
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
?
的证明
几
何
解
释:
a
a
b
b
a2
ab
ab
b2
a2+2ab+b2
(a+b)2=
结构特征:
左边是
的平方;
二项式
(两数和)
右边是
两数的平方和
加上
这两数乘积的两倍.
三项式:
两数和
的平方
等于这两数的平方和
加上
这两数乘积的2倍.
文字叙述:
例1.计算:
(1)(2a+3b)2
解:原式=(2a)2+2·2a·3b+(3b)2
=4a2+12ab+9b2
(2)(2a+
)2
解:原式=(2a)2+2·2a·
+(
)2
=4a2+2ab+
例2.计算:
(1)(a-b)2
解:原式=【a+(-b)】2
=a2+2·a·(-b)+(-b)2
=a2-2ab+b2
(2)(2m-3n)2
解:原式=【2m+(-3n)】2
=(2m)2+2·2m·(-3n)+(-3n)2
=4m2-12mn+9n2
得出:两数差的平方公式(完全平方差公式)
(a-b)2=a2-2ab+b2
两数差的平方等于它们的平方和减去这两数积的2倍.
文字叙述:
例3.计算:
(1)(2x-y)2
解:原式=(2x)2-2·2x·y+y2
=4x2-4xy+y2
(2)(
a-2b)2
解:原式=(
a)2-2·
a·2b+(2b)2
=
a2-6ab+4b2
(a+b)2
=
a2+2ab+b2
.
(a?b)2
=
a2?2ab+b2
.
完全平方
公式
拓展例题:
已知
x-y=5
,xy=6.
求代数式x2+y2的值.
解法一:x2+y2=(x-y)2+2xy
=52+2×6=37
解法二:∵
x-y=5
∴两边同时平方,有:
(x-y)2=52
x2-2xy+y2=25
∵xy=6
∴x2-2×6+y2=25
解得:
x2+y2=25+12=37
四,练习:
1.计算:
(1)
(x+3)2
(2)
(3m-n)2
(3)(2x+y)2
(4)(
a-
b)2
解:(1)原式=x2+6x+9
(2)原式=9m2-6mn+n2
(3)原式=4x2+4xy+y2
(4)原式=
a2-
ab+
b2
2.(能力提升)
若︱x+y-5︱+(xy-6)2=0
求代数式x2+y2的值.
解:
∵︱x+y-5︱+(xy-6)2=0
∴
x+y-5=0
xy-6=0
解得:
x+y=5
xy=6
方法一:∴
x2+y2=(x+y)2-2xy
=52-6×2=13
方法二:把x+y=5
两边同时平方:
(x+y)2=52
x2+2xy+y2=25
∴x2+y2=25-2xy
=25-2×6
=13
五.小结:
1.两数和的平方(完全平方和公式)
(a+b)2=a2+2ab+b2
2.两数差的平方(完全平方差公式)
(a-b)2=a2-2ab+b2
3.公式的运用,关键在于找到两个数,哪一个数
相当于公式中的a,哪一个相当于公式中的b
六,作业:
1.计算:
(1)
(3a+b)2
(2)
(2a-4b)2
(3)
(2x+
y)2
(4)
(
x-
y)2
答案:
(1)
9a2+6ab+b2
(2)
4a2-16ab+16b2
(3)
4x2+
xy+
y2
(4)
x2-
xy+
y2
2.填空:
(1)
a2+6a+_______=(a+____)2
(2)
4x2-20x+_______=(2x-____)2
(3)
a2+b2=(a-b)2+__________
(4)
(x-y)2+________=(x+y)2
答案:
(1)9
,
3
(2)
25
,
5
(3)
2ab
(4)4xy
3.(能力提升)
(1)
如果
a2+b2-6a+10b+34=0
求
a+b
的值.
(2)若代数式
x2+kx+121是一个完全平方式,则常数项k为_______
(3)多项式9x2+1加上一个单项式后,使它能成为一个整式的完全平方,请写出所有可能的单项式.
答案:
(1)
-2
(2)±22
(3)
6x
-6x
,
-1
,
x4
,
-9x2
本节课你的收获是什么?
小结
本节课你学到了什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果
是三项,
即
(a
?b)2=a2
?2ab+b2;
平方差公式的结果
是两项,
即
(a+b)(a?b)=a2?b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边,
做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号,
是运用完全平方公式进行多项式乘法的关键
拓展:
1.计算:
2.已知 求下列各式的值.
(1).
(2).
标题
两数和的平方
标题
回顾与思考
公式的结构特征:
左边是
a2
?
b2;
两个二项式的乘积,
平方差公式
回顾
&
思考
?
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
两数的平方差.
2.计算下列各题:
=
=
=
m2+4m+4
完
全
平
方
公
式
一块边长为a米的正方形实验田,
做一做
图1—6
a
因需要将其边长增加
b
米。
形成四块实验田,以种植不同的新品种(如图1—6).
用不同的形式表示实验田的总面积,
并进行比较.
a
b
b
法一
直
接
求
总面积=
(a+b)
;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
你发现了什么?
探索:
2
公式:
完全平方公式
动脑筋
想一想
(a+b)2=a2+2ab+b2
;
(a+b)2
=
推证
?
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
?
的证明
几
何
解
释:
a
a
b
b
a2
ab
ab
b2
a2+2ab+b2
(a+b)2=
结构特征:
左边是
的平方;
二项式
(两数和)
右边是
两数的平方和
加上
这两数乘积的两倍.
三项式:
两数和
的平方
等于这两数的平方和
加上
这两数乘积的2倍.
文字叙述:
例1.计算:
(1)(2a+3b)2
解:原式=(2a)2+2·2a·3b+(3b)2
=4a2+12ab+9b2
(2)(2a+
)2
解:原式=(2a)2+2·2a·
+(
)2
=4a2+2ab+
例2.计算:
(1)(a-b)2
解:原式=【a+(-b)】2
=a2+2·a·(-b)+(-b)2
=a2-2ab+b2
(2)(2m-3n)2
解:原式=【2m+(-3n)】2
=(2m)2+2·2m·(-3n)+(-3n)2
=4m2-12mn+9n2
得出:两数差的平方公式(完全平方差公式)
(a-b)2=a2-2ab+b2
两数差的平方等于它们的平方和减去这两数积的2倍.
文字叙述:
例3.计算:
(1)(2x-y)2
解:原式=(2x)2-2·2x·y+y2
=4x2-4xy+y2
(2)(
a-2b)2
解:原式=(
a)2-2·
a·2b+(2b)2
=
a2-6ab+4b2
(a+b)2
=
a2+2ab+b2
.
(a?b)2
=
a2?2ab+b2
.
完全平方
公式
拓展例题:
已知
x-y=5
,xy=6.
求代数式x2+y2的值.
解法一:x2+y2=(x-y)2+2xy
=52+2×6=37
解法二:∵
x-y=5
∴两边同时平方,有:
(x-y)2=52
x2-2xy+y2=25
∵xy=6
∴x2-2×6+y2=25
解得:
x2+y2=25+12=37
四,练习:
1.计算:
(1)
(x+3)2
(2)
(3m-n)2
(3)(2x+y)2
(4)(
a-
b)2
解:(1)原式=x2+6x+9
(2)原式=9m2-6mn+n2
(3)原式=4x2+4xy+y2
(4)原式=
a2-
ab+
b2
2.(能力提升)
若︱x+y-5︱+(xy-6)2=0
求代数式x2+y2的值.
解:
∵︱x+y-5︱+(xy-6)2=0
∴
x+y-5=0
xy-6=0
解得:
x+y=5
xy=6
方法一:∴
x2+y2=(x+y)2-2xy
=52-6×2=13
方法二:把x+y=5
两边同时平方:
(x+y)2=52
x2+2xy+y2=25
∴x2+y2=25-2xy
=25-2×6
=13
五.小结:
1.两数和的平方(完全平方和公式)
(a+b)2=a2+2ab+b2
2.两数差的平方(完全平方差公式)
(a-b)2=a2-2ab+b2
3.公式的运用,关键在于找到两个数,哪一个数
相当于公式中的a,哪一个相当于公式中的b
六,作业:
1.计算:
(1)
(3a+b)2
(2)
(2a-4b)2
(3)
(2x+
y)2
(4)
(
x-
y)2
答案:
(1)
9a2+6ab+b2
(2)
4a2-16ab+16b2
(3)
4x2+
xy+
y2
(4)
x2-
xy+
y2
2.填空:
(1)
a2+6a+_______=(a+____)2
(2)
4x2-20x+_______=(2x-____)2
(3)
a2+b2=(a-b)2+__________
(4)
(x-y)2+________=(x+y)2
答案:
(1)9
,
3
(2)
25
,
5
(3)
2ab
(4)4xy
3.(能力提升)
(1)
如果
a2+b2-6a+10b+34=0
求
a+b
的值.
(2)若代数式
x2+kx+121是一个完全平方式,则常数项k为_______
(3)多项式9x2+1加上一个单项式后,使它能成为一个整式的完全平方,请写出所有可能的单项式.
答案:
(1)
-2
(2)±22
(3)
6x
-6x
,
-1
,
x4
,
-9x2
本节课你的收获是什么?
小结
本节课你学到了什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果
是三项,
即
(a
?b)2=a2
?2ab+b2;
平方差公式的结果
是两项,
即
(a+b)(a?b)=a2?b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边,
做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号,
是运用完全平方公式进行多项式乘法的关键
拓展:
1.计算:
2.已知 求下列各式的值.
(1).
(2).
