【人教七上数学教学课件】2.1.1 用字母表示数 课件(共23张PPT)
文档属性
| 名称 | 【人教七上数学教学课件】2.1.1 用字母表示数 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 21:03:42 | ||
图片预览








文档简介
(共23张PPT)
第二章
整式的加减
2.1
第1课时
用字母表示数
随堂演练
课堂小结
获取新知
例题讲解
知识回顾
情景导入
我们小学学过了各种公式,你还能记得多少?
三角形面积公式
长方形面积公式
正方形面积公式
圆的面积公式
梯形面积公式
圆柱体的体积公式
行程问题
知识回顾
s=vt
科学家爱因斯坦上小学时,在一次数学课中,发现
了下列的等式:
1+2=2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把
这个规律告诉了他的老师和同学,得到了大家的赞赏.
情景导入
a+b=b+a
例题讲解
例1
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a
cm,高是h
cm,用式子表示它的
体积;
(4)用式子表示数n的相反数.
0.8p
mn
a2h
-n
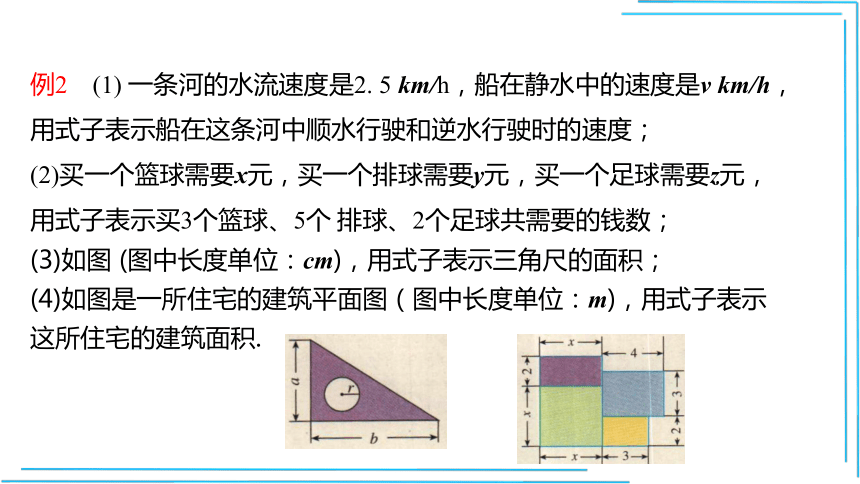
例2
(1)
一条河的水流速度是2.
5
km/h,船在静水中的速度是v
km/h,
用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,
用式子表示买3个篮球、5个
排球、2个足球共需要的钱数;
(3)如图
(图中长度单位:cm),用式子表示三角尺的面积;
(4)如图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
分析:(1)船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中
的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是(
v+2.
5)
km/h,
逆水行驶的速度是
(v-2.
5)
km/h.
(2)买3个篮球、5个排球、2个足球共需(
3x+5y+2z)元.
三角尺的面积等于三角形的面积减去圆的面积.根据图中的
数据,得三角形的面积是积是πr2
cm2.因此三角尺的面积
(cm2)
(4)住宅的建筑面积等于四个长方形面积的和.根据图中标出的尺寸,可得这所住宅的建筑面积是(x2+2x+18)(m2)
备注:用字母表示数,字母和数一样可以参与运算,还可以把数量关系简明的表示出来.
把文字“翻译”成含字母的式子时,首先要根据有关数学知识理解题目的含义,要找出各个量之间的关系,抓住关键词语,明确它们之间的意义及联系,如和、差、积、商、多、少等,注意数量关系的运算顺序,正确使用运算符号和括号.
同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
(1)全校学生总数是x,其中女生占总数52%,
则女生人数是
,男生人数是
;
(2)一个数比a的2倍小5,则这个数为
;
(3)5箱苹果重m
kg,每箱重
kg
;
(4)某班有a名学生,现把一批图书分给全班
学生阅读,如果每人分4本,还缺25本,
则这批图书共
本;
(5)小红出生时爸爸28岁,小红a岁时,
爸爸
岁.
例3
填空:
数与字母相乘时,
数字通常写在字母的左边,乘号通常省略不写或写成“·”
遇到除法时,一般用分数的形式来写;
在实际问题中含有单位时,若式子含有和或差关系则用括号括起来
(a+28)
用字母表示数的书写规则:
(1)字母与字母相乘时,“×”号通常省略不写或写成“·”;
(2)字母与数相乘时,数通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式.
(5)在实际问题中含有单位时,若式子含有和或差关系则用括号括起来.
例4
用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子
枚(用含n的代数式表示).
方法一:除第一个图形有4枚棋子外,每多一个图形,多3枚棋子.
4+3(n-1)=3
n+1
第1个图
第2个图
第3个图
…
第1个图
第2个图
第3个图
…
方法二:每个图形,可看成是序列数与3的倍数又多1枚棋子:3n+1
第1个图
第2个图
第3个图
…
方法三:
2n+(n+1)=3n+1
随堂演练
1.下列含有字母的式子符合书写规范的是( )
A.1a
B.
b
C.0.5xy
D.(x+y)÷z
C
2.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为(
)
A.(a+b)元
B.3(a+b)元
C.(3a+b)元
D.(a+3b)元
D
3.如图,是两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A.πR2
B.πr2
C.πR2+πr2
D.πR2-πr2
D
A
4.
“比a
的
倍大1的数”用式子表示为( )
5.填空:
(1)买单价为6元的钢笔a支,共需________元;
(2)一台电视机的标价为a元,则打八折后的售价为
________
元;
(3)温度由30
℃下降t
℃后是________℃.
6a
0.8a
(30-t)
6.
如图,用火柴棒拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棒?
第一个正方形可以看成是1根火柴棒加3根火柴棒搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要
根
7.观察下列各式:
9-1=8,
16-4=12,25-9=16,36-16=20…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n
的等式表示这个规律.
32-12=4×2,
42-22=4×3,
52-32=4×4,
62-42=4×5…
(n+2)2-n2=4(n+1),
解:
课堂小结
用字母表示数
书写规则
(1)字母与字母相乘时,“×”号通常省略不写或写成“·”;
(2)字母与数相乘时,数通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式.
(5)在实际问题中含有单位时,若式子含有和或差关系则用括号括起来.
一般性、限制性、普遍性
特点
https://www.21cnjy.com/help/help_extract.php
第二章
整式的加减
2.1
第1课时
用字母表示数
随堂演练
课堂小结
获取新知
例题讲解
知识回顾
情景导入
我们小学学过了各种公式,你还能记得多少?
三角形面积公式
长方形面积公式
正方形面积公式
圆的面积公式
梯形面积公式
圆柱体的体积公式
行程问题
知识回顾
s=vt
科学家爱因斯坦上小学时,在一次数学课中,发现
了下列的等式:
1+2=2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把
这个规律告诉了他的老师和同学,得到了大家的赞赏.
情景导入
a+b=b+a
例题讲解
例1
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a
cm,高是h
cm,用式子表示它的
体积;
(4)用式子表示数n的相反数.
0.8p
mn
a2h
-n
例2
(1)
一条河的水流速度是2.
5
km/h,船在静水中的速度是v
km/h,
用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,
用式子表示买3个篮球、5个
排球、2个足球共需要的钱数;
(3)如图
(图中长度单位:cm),用式子表示三角尺的面积;
(4)如图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
分析:(1)船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中
的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是(
v+2.
5)
km/h,
逆水行驶的速度是
(v-2.
5)
km/h.
(2)买3个篮球、5个排球、2个足球共需(
3x+5y+2z)元.
三角尺的面积等于三角形的面积减去圆的面积.根据图中的
数据,得三角形的面积是积是πr2
cm2.因此三角尺的面积
(cm2)
(4)住宅的建筑面积等于四个长方形面积的和.根据图中标出的尺寸,可得这所住宅的建筑面积是(x2+2x+18)(m2)
备注:用字母表示数,字母和数一样可以参与运算,还可以把数量关系简明的表示出来.
把文字“翻译”成含字母的式子时,首先要根据有关数学知识理解题目的含义,要找出各个量之间的关系,抓住关键词语,明确它们之间的意义及联系,如和、差、积、商、多、少等,注意数量关系的运算顺序,正确使用运算符号和括号.
同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
(1)全校学生总数是x,其中女生占总数52%,
则女生人数是
,男生人数是
;
(2)一个数比a的2倍小5,则这个数为
;
(3)5箱苹果重m
kg,每箱重
kg
;
(4)某班有a名学生,现把一批图书分给全班
学生阅读,如果每人分4本,还缺25本,
则这批图书共
本;
(5)小红出生时爸爸28岁,小红a岁时,
爸爸
岁.
例3
填空:
数与字母相乘时,
数字通常写在字母的左边,乘号通常省略不写或写成“·”
遇到除法时,一般用分数的形式来写;
在实际问题中含有单位时,若式子含有和或差关系则用括号括起来
(a+28)
用字母表示数的书写规则:
(1)字母与字母相乘时,“×”号通常省略不写或写成“·”;
(2)字母与数相乘时,数通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式.
(5)在实际问题中含有单位时,若式子含有和或差关系则用括号括起来.
例4
用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子
枚(用含n的代数式表示).
方法一:除第一个图形有4枚棋子外,每多一个图形,多3枚棋子.
4+3(n-1)=3
n+1
第1个图
第2个图
第3个图
…
第1个图
第2个图
第3个图
…
方法二:每个图形,可看成是序列数与3的倍数又多1枚棋子:3n+1
第1个图
第2个图
第3个图
…
方法三:
2n+(n+1)=3n+1
随堂演练
1.下列含有字母的式子符合书写规范的是( )
A.1a
B.
b
C.0.5xy
D.(x+y)÷z
C
2.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为(
)
A.(a+b)元
B.3(a+b)元
C.(3a+b)元
D.(a+3b)元
D
3.如图,是两同心圆,大圆半径为R,小圆半径为r,则阴影部分的面积为( )
A.πR2
B.πr2
C.πR2+πr2
D.πR2-πr2
D
A
4.
“比a
的
倍大1的数”用式子表示为( )
5.填空:
(1)买单价为6元的钢笔a支,共需________元;
(2)一台电视机的标价为a元,则打八折后的售价为
________
元;
(3)温度由30
℃下降t
℃后是________℃.
6a
0.8a
(30-t)
6.
如图,用火柴棒拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棒?
第一个正方形可以看成是1根火柴棒加3根火柴棒搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要
根
7.观察下列各式:
9-1=8,
16-4=12,25-9=16,36-16=20…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n
的等式表示这个规律.
32-12=4×2,
42-22=4×3,
52-32=4×4,
62-42=4×5…
(n+2)2-n2=4(n+1),
解:
课堂小结
用字母表示数
书写规则
(1)字母与字母相乘时,“×”号通常省略不写或写成“·”;
(2)字母与数相乘时,数通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式.
(5)在实际问题中含有单位时,若式子含有和或差关系则用括号括起来.
一般性、限制性、普遍性
特点
https://www.21cnjy.com/help/help_extract.php
