【人教七上数学教学课件】2.1.2 单项式 课件(共19张PPT)
文档属性
| 名称 | 【人教七上数学教学课件】2.1.2 单项式 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 21:02:50 | ||
图片预览




文档简介
(共19张PPT)
第二章
整式的加减
2.1
第2课时
单项式
随堂演练
课堂小结
获取新知
例题讲解
情景导入
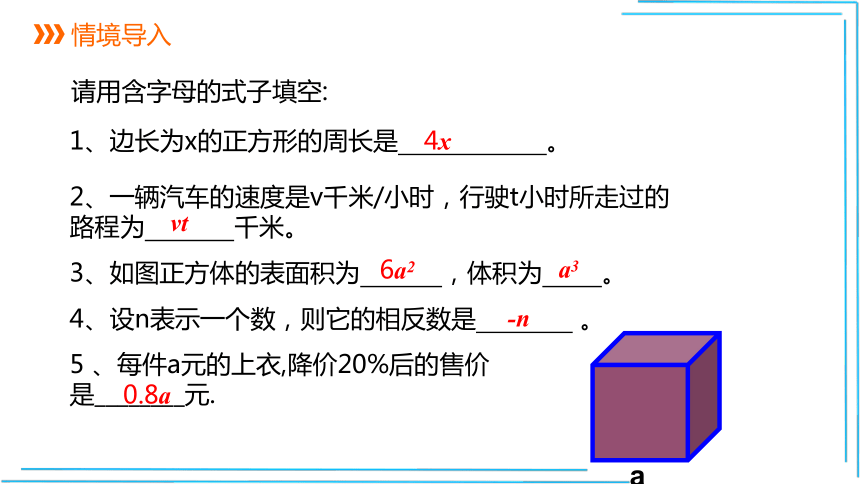
请用含字母的式子填空:
1、边长为x的正方形的周长是
。
2、一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为
千米。
3、如图正方体的表面积为
,体积为
。
4、设n表示一个数,则它的相反数是
。
4x
vt
6a2
a3
-n
5
、每件a元的上衣,降价20%后的售价是________元.
0.8a
a
情境导入
获取新知
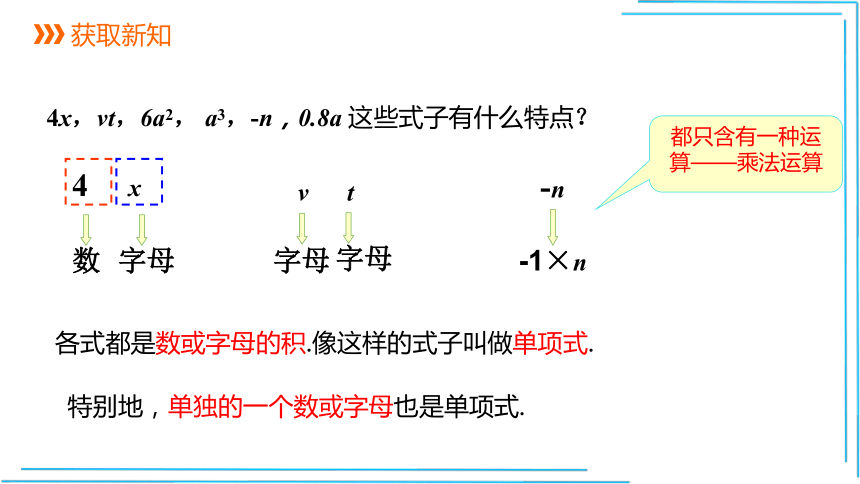
4x,vt,6a2,
a3,-n,0.8a
这些式子有什么特点?
各式都是数或字母的积.像这样的式子叫做单项式.
特别地,单独的一个数或字母也是单项式.
v
t
-n
数
字母
字母
-1×n
都只含有一种运算——乘法运算
4
x
字母
判断单项式的方法
例1
下列式子中,单项式有哪些?
(1)-3;
(2)
x2y;
(3)
;
(4)
;
(5)-
ab2;
(6)
;
(7)
n2;
(8)
π+2.
解:单项式有(1)(2)(4)(5)(7)(8).
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.可以含有除以数的运算,不能含有除以字母的运算.
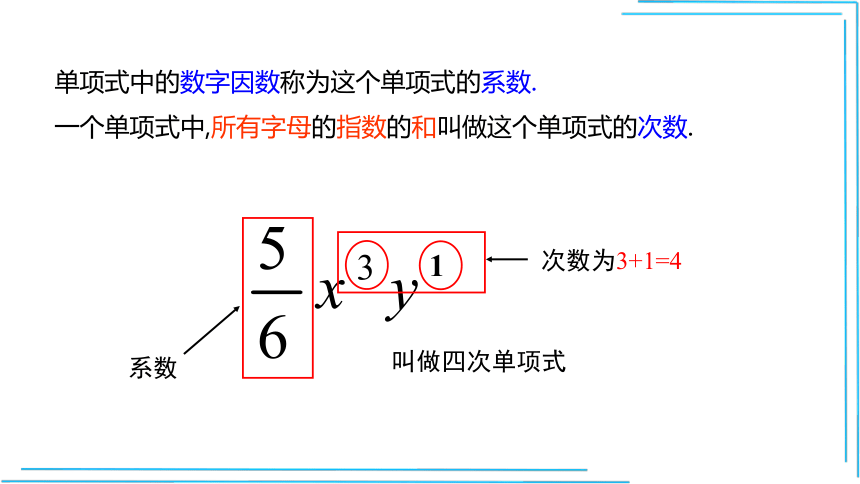
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
叫做四次单项式
次数为3+1=4
例题讲解
例2
用单项式填空,并指出它们的次数:
(1)每包书有12册,n包书有
册;
(2)底边长为a
cm,高为hcm的三角形的面积是
cm2;
(3)棱长为a
cm的正方体的体积是
cm3
;
(4)一台电视机原价b元,现按原价的9折出售,
这台电视机现在的售价是
元;
(5)一个长方形的长是0.9m,宽是b
m,这个长方形的面积是
m2.
12n
a3
0.9b
0.9b
解:
(1)12n,它的系数是12,次数是1;
(2)
,
它的系数是
,次数是2;
(3)a3,
它的系数是1,次数是3;
(4)
0.9b,它的系数是0.9,次数是1;
(5)
0.9b,它的系数是0.9,次数是1.
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③系数包括它前面的符号
④当单项式的系数是带分数时要写成假分数的形式
⑤省略1的字母指数别漏掉;
⑥单项式次数只与字母指数有关.
⑦单独的数字不含字母,所以它的次数是零次.
系数
次数
例3
5x4-my
与6xmy3的次数相同,求m的值.
解:由题意可得:
4-m+1=m+3
m=1
备注:根据单项式的系数与次数的概念建立与要求字母有关的简易方程即可求出要求字母的值,体现了转化思想和方程思想.
2.下列说法中,正确的是( )
A.
的系数是
B.
的系数是
C.3ab2的系数是3a
D.
的系数是
A
D
1.单项式2a的系数是( )
A.2
B.2a
C.1
D.a
随堂演练
D
3.下列说法中,正确的是( )
A.单项式一定是含字母的式子
B.单项式a没有系数
C.-y的次数为0
D.单项式-π2x2y的系数是-π2,次数是3
4.下列说法中正确的是(
)
A.单项式
的系数是-2,次数是4
B.单项式
的系数是0,次数是0
C.单项式
的系数是-5,次数是6
D.单项式
的系数是
,次数是6
D
5.已知2kx2yn是关于x,y的一个单项式,且系数是7,次数是5,那么k=____,n=_____.
3
6.
单项式
5
R?
的系数是
,次数是
;
5π
2
7.
说出下列各单项式的系数和次数:
(1)
;
(2)-3ab;
(3)
;
(4)-22a3b5;
(5)-x.
解:(1)
的系数是
,次数是6.
(2)-3ab的系数是-3,次数是2.
(3)
的系数是
,次数是3.
(4)-22a3b5的系数是-22,即-4,次数是8.
(5)-x的系数是-1,次数是1.
8.若
是关于
x,y
的一个四次单项式,
m,n应满足的条件?
所以m≠
2,n=2.
2+n=4,
m-2
≠
0,
解:由题意知m,n要满足
课堂小结
单项式
定义
系数
次数
数或字母的积,单独的一个数或字母也是单项式
单项式中的数字因数
所有字母的指数的和
https://www.21cnjy.com/help/help_extract.php
第二章
整式的加减
2.1
第2课时
单项式
随堂演练
课堂小结
获取新知
例题讲解
情景导入
请用含字母的式子填空:
1、边长为x的正方形的周长是
。
2、一辆汽车的速度是v千米/小时,行驶t小时所走过的路程为
千米。
3、如图正方体的表面积为
,体积为
。
4、设n表示一个数,则它的相反数是
。
4x
vt
6a2
a3
-n
5
、每件a元的上衣,降价20%后的售价是________元.
0.8a
a
情境导入
获取新知
4x,vt,6a2,
a3,-n,0.8a
这些式子有什么特点?
各式都是数或字母的积.像这样的式子叫做单项式.
特别地,单独的一个数或字母也是单项式.
v
t
-n
数
字母
字母
-1×n
都只含有一种运算——乘法运算
4
x
字母
判断单项式的方法
例1
下列式子中,单项式有哪些?
(1)-3;
(2)
x2y;
(3)
;
(4)
;
(5)-
ab2;
(6)
;
(7)
n2;
(8)
π+2.
解:单项式有(1)(2)(4)(5)(7)(8).
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.可以含有除以数的运算,不能含有除以字母的运算.
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
叫做四次单项式
次数为3+1=4
例题讲解
例2
用单项式填空,并指出它们的次数:
(1)每包书有12册,n包书有
册;
(2)底边长为a
cm,高为hcm的三角形的面积是
cm2;
(3)棱长为a
cm的正方体的体积是
cm3
;
(4)一台电视机原价b元,现按原价的9折出售,
这台电视机现在的售价是
元;
(5)一个长方形的长是0.9m,宽是b
m,这个长方形的面积是
m2.
12n
a3
0.9b
0.9b
解:
(1)12n,它的系数是12,次数是1;
(2)
,
它的系数是
,次数是2;
(3)a3,
它的系数是1,次数是3;
(4)
0.9b,它的系数是0.9,次数是1;
(5)
0.9b,它的系数是0.9,次数是1.
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③系数包括它前面的符号
④当单项式的系数是带分数时要写成假分数的形式
⑤省略1的字母指数别漏掉;
⑥单项式次数只与字母指数有关.
⑦单独的数字不含字母,所以它的次数是零次.
系数
次数
例3
5x4-my
与6xmy3的次数相同,求m的值.
解:由题意可得:
4-m+1=m+3
m=1
备注:根据单项式的系数与次数的概念建立与要求字母有关的简易方程即可求出要求字母的值,体现了转化思想和方程思想.
2.下列说法中,正确的是( )
A.
的系数是
B.
的系数是
C.3ab2的系数是3a
D.
的系数是
A
D
1.单项式2a的系数是( )
A.2
B.2a
C.1
D.a
随堂演练
D
3.下列说法中,正确的是( )
A.单项式一定是含字母的式子
B.单项式a没有系数
C.-y的次数为0
D.单项式-π2x2y的系数是-π2,次数是3
4.下列说法中正确的是(
)
A.单项式
的系数是-2,次数是4
B.单项式
的系数是0,次数是0
C.单项式
的系数是-5,次数是6
D.单项式
的系数是
,次数是6
D
5.已知2kx2yn是关于x,y的一个单项式,且系数是7,次数是5,那么k=____,n=_____.
3
6.
单项式
5
R?
的系数是
,次数是
;
5π
2
7.
说出下列各单项式的系数和次数:
(1)
;
(2)-3ab;
(3)
;
(4)-22a3b5;
(5)-x.
解:(1)
的系数是
,次数是6.
(2)-3ab的系数是-3,次数是2.
(3)
的系数是
,次数是3.
(4)-22a3b5的系数是-22,即-4,次数是8.
(5)-x的系数是-1,次数是1.
8.若
是关于
x,y
的一个四次单项式,
m,n应满足的条件?
所以m≠
2,n=2.
2+n=4,
m-2
≠
0,
解:由题意知m,n要满足
课堂小结
单项式
定义
系数
次数
数或字母的积,单独的一个数或字母也是单项式
单项式中的数字因数
所有字母的指数的和
https://www.21cnjy.com/help/help_extract.php
