【人教八上数学教学课件】13.1.1轴对称 课件(共30张PPT)
文档属性
| 名称 | 【人教八上数学教学课件】13.1.1轴对称 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 20:59:54 | ||
图片预览







文档简介
(共30张PPT)
第十三章
轴对称
13.1 轴对称
随堂演练
获取新知
情境导入
例题讲解
课堂小结
13.1.1
轴对称
情境导入
生活中,从自然景观到艺术作品,对称现象无处不在
获取新知
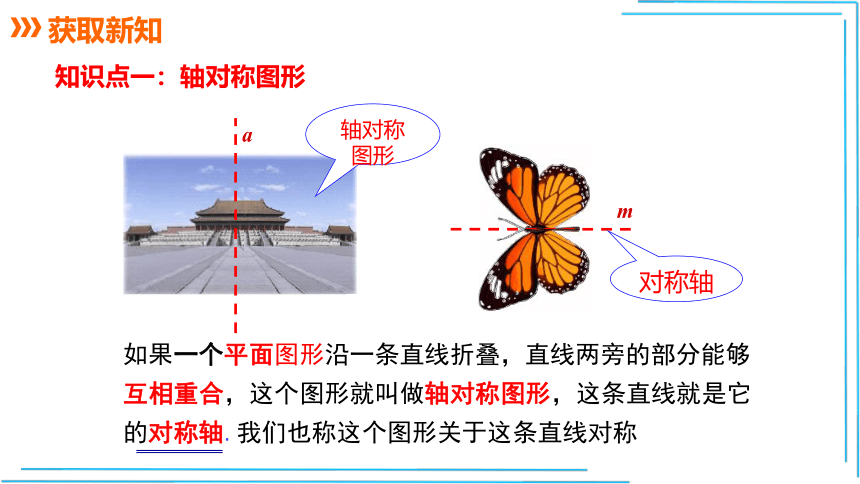
知识点一:轴对称图形
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.我们也称这个图形关于这条直线对称
轴对称图形
对称轴
a
m
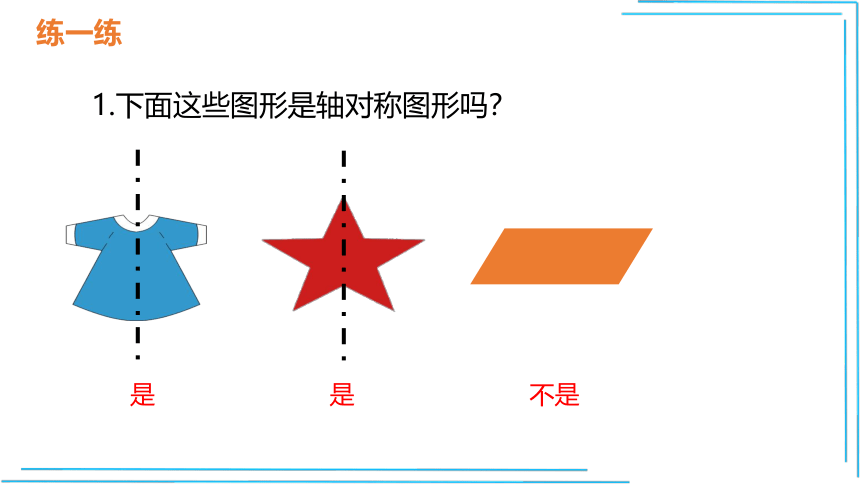
是
是
不是
1.下面这些图形是轴对称图形吗?
练一练
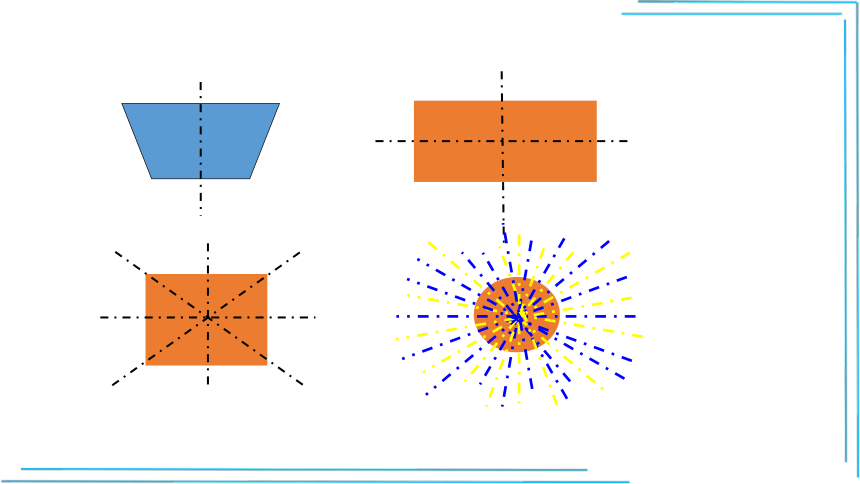
2.下面这些图形是轴对称图形吗?如果是,有几条对称轴?
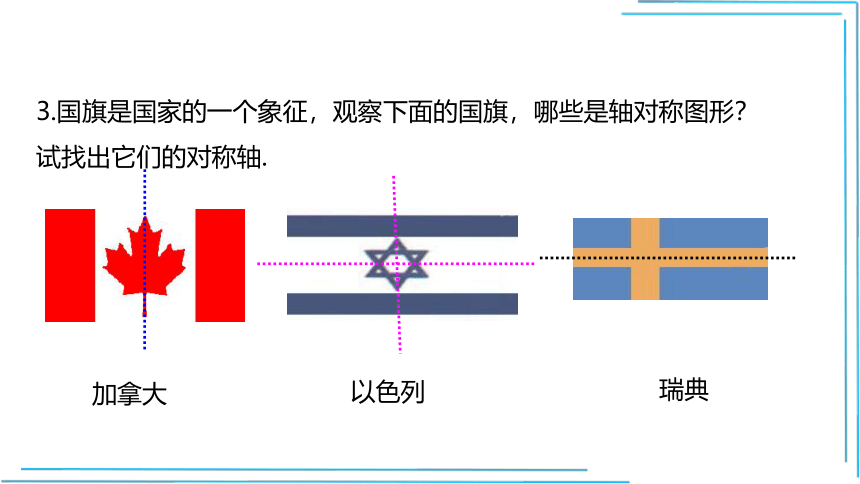
3.国旗是国家的一个象征,观察下面的国旗,哪些是轴对称图形?试找出它们的对称轴.
加拿大
瑞典
以色列
1、有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
2、对称轴通常画成虚线,是直线,不能画成线段.
总
结
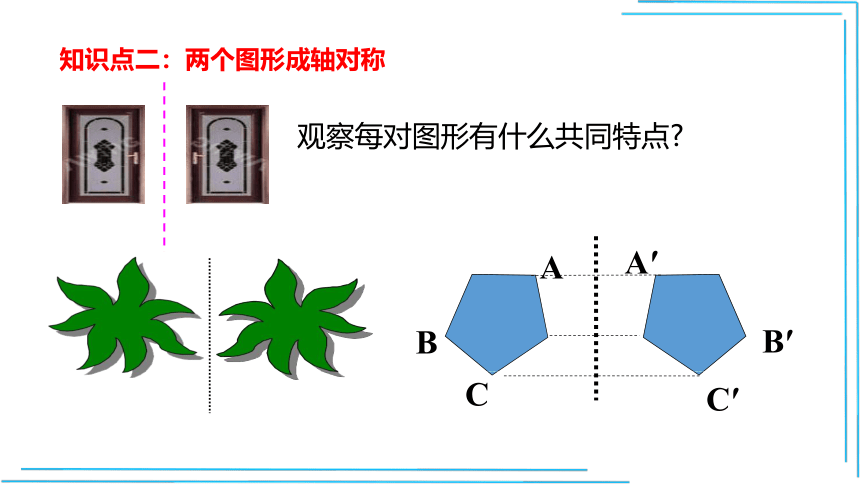
知识点二:两个图形成轴对称
A′
A
B
C
B′
C′
观察每对图形有什么共同特点?
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.折叠后重合的点是对应点,叫做对称点
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
____的对称点是点E
点D
点A的对称点是点F
能重合的点叫_________.
对称点
点B
m
A
B
C
D
F
E
点C的对称点是_____
练
习
例题讲解
例
下列四组图片中有哪几组图形成轴对称?
B
D
C
A
轴对称与轴对称图形的区别与联系
名称
关系
轴对称
轴对称图形
区别
意义不同
两个图形之间的对称关系
具有特殊位置关系的图形
对象不同
两个图形
一个图形
对称轴的位置不同
在两个图形之间
过图形的某条直线
联系
(1)如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形;(2)如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两个图形就成轴对称
归纳
知识点三:轴对称的性质
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)对称轴分成的两部分全等吗?
(1)
(2)
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
思
考
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
线段垂直平分线的定义
图形轴对称的性质
知识要点
一个轴对称图形的对称轴是否也具有上述性质呢?
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称图形的性质
A
B
A
′
B
′
M
N
如图,MN垂直平分AA
′,
MN垂直平分BB
′.
知识要点
例题讲解
例1
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
A
例2
如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).故选B.
B
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
随堂演练
C
1.下列图形中,是轴对称图形的是( )
图D-16-1
2.下列“数字”图形中,有且仅有一条对称轴的是( )
图D-16-2
A
3.如图D-16-4所示,如果直线m是五边形ABCDE的对称轴,其中∠A=115°,∠ABC=120°,那么∠BCD的度数为________,连接BD交直线m于点F,则BF________DF(填“=”“>”或“<”),BD________m(填“垂直于”或“不垂直于”).
图D-16-4
70°
=
垂直于
课堂小结
轴对称
轴对称
轴对称图形
性质
定义
性质
轴对称与
轴对称图形
联系
区别
线段的垂直平分线
定义
https://www.21cnjy.com/help/help_extract.php
第十三章
轴对称
13.1 轴对称
随堂演练
获取新知
情境导入
例题讲解
课堂小结
13.1.1
轴对称
情境导入
生活中,从自然景观到艺术作品,对称现象无处不在
获取新知
知识点一:轴对称图形
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.我们也称这个图形关于这条直线对称
轴对称图形
对称轴
a
m
是
是
不是
1.下面这些图形是轴对称图形吗?
练一练
2.下面这些图形是轴对称图形吗?如果是,有几条对称轴?
3.国旗是国家的一个象征,观察下面的国旗,哪些是轴对称图形?试找出它们的对称轴.
加拿大
瑞典
以色列
1、有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条.
2、对称轴通常画成虚线,是直线,不能画成线段.
总
结
知识点二:两个图形成轴对称
A′
A
B
C
B′
C′
观察每对图形有什么共同特点?
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.折叠后重合的点是对应点,叫做对称点
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
____的对称点是点E
点D
点A的对称点是点F
能重合的点叫_________.
对称点
点B
m
A
B
C
D
F
E
点C的对称点是_____
练
习
例题讲解
例
下列四组图片中有哪几组图形成轴对称?
B
D
C
A
轴对称与轴对称图形的区别与联系
名称
关系
轴对称
轴对称图形
区别
意义不同
两个图形之间的对称关系
具有特殊位置关系的图形
对象不同
两个图形
一个图形
对称轴的位置不同
在两个图形之间
过图形的某条直线
联系
(1)如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形;(2)如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两个图形就成轴对称
归纳
知识点三:轴对称的性质
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)对称轴分成的两部分全等吗?
(1)
(2)
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
思
考
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
线段垂直平分线的定义
图形轴对称的性质
知识要点
一个轴对称图形的对称轴是否也具有上述性质呢?
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称图形的性质
A
B
A
′
B
′
M
N
如图,MN垂直平分AA
′,
MN垂直平分BB
′.
知识要点
例题讲解
例1
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
A
例2
如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).故选B.
B
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
随堂演练
C
1.下列图形中,是轴对称图形的是( )
图D-16-1
2.下列“数字”图形中,有且仅有一条对称轴的是( )
图D-16-2
A
3.如图D-16-4所示,如果直线m是五边形ABCDE的对称轴,其中∠A=115°,∠ABC=120°,那么∠BCD的度数为________,连接BD交直线m于点F,则BF________DF(填“=”“>”或“<”),BD________m(填“垂直于”或“不垂直于”).
图D-16-4
70°
=
垂直于
课堂小结
轴对称
轴对称
轴对称图形
性质
定义
性质
轴对称与
轴对称图形
联系
区别
线段的垂直平分线
定义
https://www.21cnjy.com/help/help_extract.php
