2.4 线段、角的轴对称性课件 2021—2022学年苏科版八年级数学上册(19张)
文档属性
| 名称 | 2.4 线段、角的轴对称性课件 2021—2022学年苏科版八年级数学上册(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 112.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 08:36:40 | ||
图片预览





文档简介
(共19张PPT)
2.4
线段、角的轴对称性(4)
复习回顾
1.线段是
图形,它有
,
分别为:
和
.
轴对称
两条对称轴
线段的垂直平分线
线段本身所在直线
2.角是
图形,对称轴是
.
轴对称
角平分线所在的直线
知识点回顾
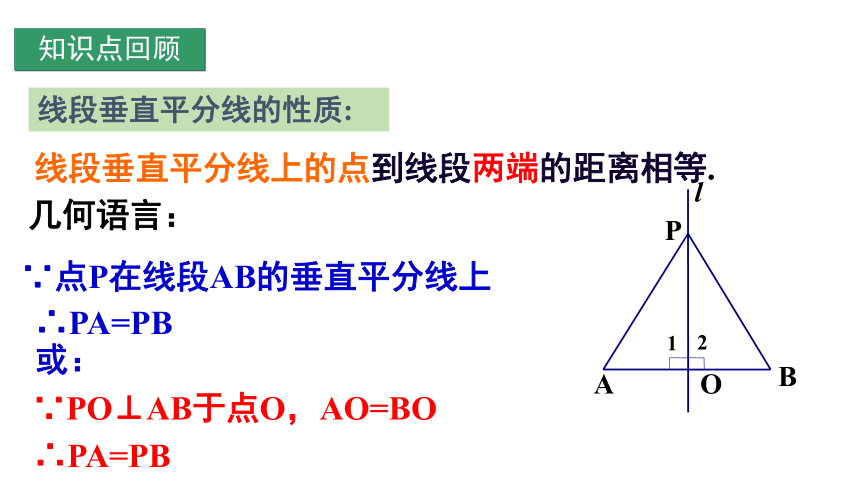
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
∵点P在线段AB的垂直平分线上
∴PA=PB
∵PO⊥AB于点O,AO=BO
∴PA=PB
2
1
l
P
O
B
A
或:
几何语言:
知识点回顾
定理
到线段两端点距离相等的点在线段的垂直平分线上。
∵PA=PB
∴P是线段AB的垂直平分线上的点
几何语言:
P
O
知识点回顾
例1.
如图,AB=AC,EB=EC,点D在AE上,你有几种方法证明DB=DC?
A
B
C
D
E
例题讲解
C
B
O
A
练习:如图,△ABC中,
AB、AC的垂直平分线l1和l2相交于点O。
求证:点O在BC的垂直平分线上。
线段垂直平分线,常向两端把线连。
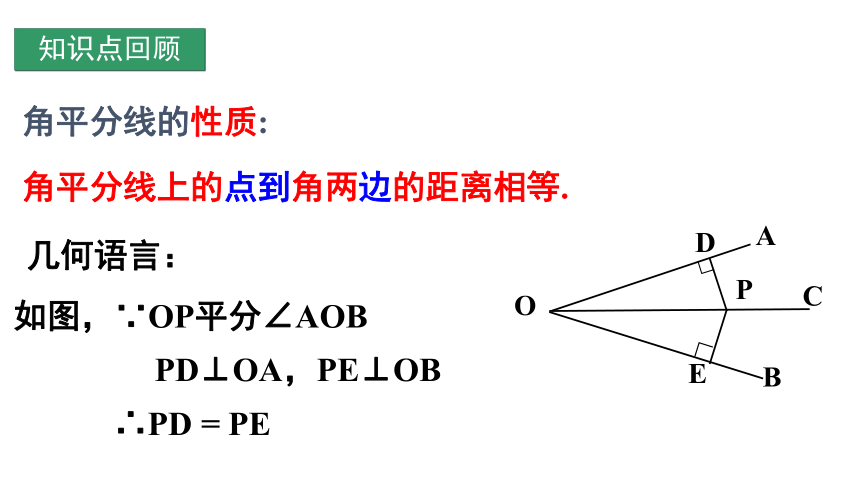
角平分线的性质:
角平分线上的点到角两边的距离相等.
PD⊥OA,PE⊥OB
几何语言:
如图,∵OP平分∠AOB
∴PD
=
PE
O
A
B
C
P
D
E
∟
∟
知识点回顾
角平分线的判定:
角的内部到角两边距离相等的点在角的平分线上.
如图,∵
QD⊥OA,
QE⊥OB
几何语言:
QD
=
QE
∴OQ平分∠AOB
O
A
B
Q
D
E
∟
∟
知识点回顾
例2
如图,△ABC的角平分线AD、BE相交于点P.
求证:点P在∠C的角平分线上.
P
A
C
B
E
D
N
M
H
∟
∟
∟
结论:
三角形的三个内角的角平分线相交于一点,该点到三角形的三边距离相等.
图中有角平分线,可向两边作垂线。
例题讲解
1、已知:
如图,
在△ABC中,
点O是∠ABC、∠ACB的外角的平分线的交点,
求证:
点O在∠A的平分线上.
O
A
C
B
E
F
N
M
H
∟
∟
∟
练一练
2.到三角形的三个顶点距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
3.到三角形的三条边距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
D
A
练一练
1、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
2、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
3、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
4、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
想想还有没有其它位置?
5、已知∠AOB和C、D两点,请在图中标出一点E,使得点E到OA、OB的距离相等,且点E到C、D的距离也相等.
O
B
A
C
D
·
·
E
画一画
∟
解:如图,
连接C、D,作线段CD的垂直平分线和∠AOB的角平分线,它们相交于点E.
则点E即为所求.
例3
已知:
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足为E、F.求证:AD垂直平分EF.
A
F
E
C
B
D
例题讲解
∟
∟
如图,在△ABC中,
D是BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB,垂足为F,EG⊥AC,交AC延长线于点G,试说明:BF=CG.
拓展练习
A
B
C
D
E
F
G
图中有角平分线,可向两边作垂线.
线段垂直平分线,常向两端把线连.
小结小结
2.4
线段、角的轴对称性(4)
复习回顾
1.线段是
图形,它有
,
分别为:
和
.
轴对称
两条对称轴
线段的垂直平分线
线段本身所在直线
2.角是
图形,对称轴是
.
轴对称
角平分线所在的直线
知识点回顾
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
∵点P在线段AB的垂直平分线上
∴PA=PB
∵PO⊥AB于点O,AO=BO
∴PA=PB
2
1
l
P
O
B
A
或:
几何语言:
知识点回顾
定理
到线段两端点距离相等的点在线段的垂直平分线上。
∵PA=PB
∴P是线段AB的垂直平分线上的点
几何语言:
P
O
知识点回顾
例1.
如图,AB=AC,EB=EC,点D在AE上,你有几种方法证明DB=DC?
A
B
C
D
E
例题讲解
C
B
O
A
练习:如图,△ABC中,
AB、AC的垂直平分线l1和l2相交于点O。
求证:点O在BC的垂直平分线上。
线段垂直平分线,常向两端把线连。
角平分线的性质:
角平分线上的点到角两边的距离相等.
PD⊥OA,PE⊥OB
几何语言:
如图,∵OP平分∠AOB
∴PD
=
PE
O
A
B
C
P
D
E
∟
∟
知识点回顾
角平分线的判定:
角的内部到角两边距离相等的点在角的平分线上.
如图,∵
QD⊥OA,
QE⊥OB
几何语言:
QD
=
QE
∴OQ平分∠AOB
O
A
B
Q
D
E
∟
∟
知识点回顾
例2
如图,△ABC的角平分线AD、BE相交于点P.
求证:点P在∠C的角平分线上.
P
A
C
B
E
D
N
M
H
∟
∟
∟
结论:
三角形的三个内角的角平分线相交于一点,该点到三角形的三边距离相等.
图中有角平分线,可向两边作垂线。
例题讲解
1、已知:
如图,
在△ABC中,
点O是∠ABC、∠ACB的外角的平分线的交点,
求证:
点O在∠A的平分线上.
O
A
C
B
E
F
N
M
H
∟
∟
∟
练一练
2.到三角形的三个顶点距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
3.到三角形的三条边距离相等的点是(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
D
A
练一练
1、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
2、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
3、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
4、如图,直线a、b、c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
c
a
b
画一画
想想还有没有其它位置?
5、已知∠AOB和C、D两点,请在图中标出一点E,使得点E到OA、OB的距离相等,且点E到C、D的距离也相等.
O
B
A
C
D
·
·
E
画一画
∟
解:如图,
连接C、D,作线段CD的垂直平分线和∠AOB的角平分线,它们相交于点E.
则点E即为所求.
例3
已知:
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足为E、F.求证:AD垂直平分EF.
A
F
E
C
B
D
例题讲解
∟
∟
如图,在△ABC中,
D是BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB,垂足为F,EG⊥AC,交AC延长线于点G,试说明:BF=CG.
拓展练习
A
B
C
D
E
F
G
图中有角平分线,可向两边作垂线.
线段垂直平分线,常向两端把线连.
小结小结
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
