12.3.2两数和(差)的平方同步练习2021—2022学年华东师大版数学八年级上册(Word版含答案)
文档属性
| 名称 | 12.3.2两数和(差)的平方同步练习2021—2022学年华东师大版数学八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 262.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览




文档简介
两数和(差)的平方
一、单选题
1.计算(a﹣2)2的结果是( )
A.a2﹣2a+4
B.a2+2a+4
C.a2﹣4a+2
D.a2﹣4a+4
2.如果二次三项式是一个完全平方式,那么m的值是(
)
A.
B.
C.4
D.
3.下列各式计算正确的是(
)
A.(a+b)(a-b)=a2+b2
B.(-a-b)(a-b)=a2-b2
C.(-n)2=-n+n2
D.(-m+n)2=m2+2mn+n2
4.已知,,,那么的值等于(
)
A.0
B.1
C.2
D.3
5.整式的最小值为(
)
A.
B.
C.
D.
6.比较与的大小,叙述正确的是(
)
A.
B.
C.由的大小确定
D.由的大小确定
7.将变形正确的是(
)
A.
B.
C.
D.
8.若,,则的值是(
)
A.-11
B.11
C.22
D.-22
9.有两个正方形A,B,现将B放在A的内部如图甲,若图甲和图乙中阴影部分面积分别为和,则正方形A,B的面积之和为( )
A.3
B.3.5
C.4
D.4.5
10.1921年伟大的中国共产党成立,2021年中国共产党迎来了百年华诞,若,则的值为(
)
A.11040
B.10520
C.8960
D.620
11.小明做了以下5道题:①(x﹣1)(x+4)=x2﹣4;②(﹣3+x)(3+x)=x2﹣9;③(﹣5x+7y)(﹣5x﹣7y)=25x2﹣49y2;④(xy﹣6)2=x2y2﹣12xy+36;⑤(﹣x﹣y)2=x2+2xy+y2,你认为小明一共做对了(
)
A.5道
B.4道
C.3道
D.2道
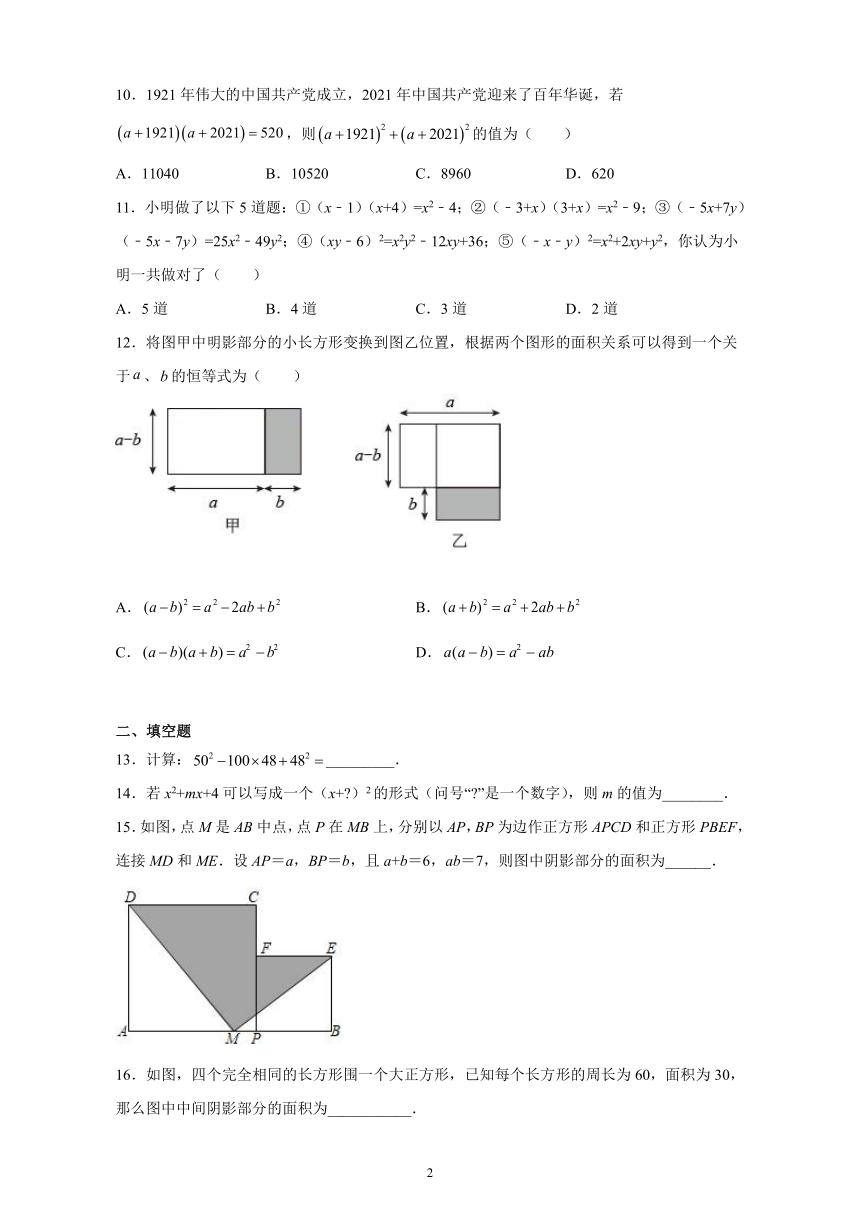
12.将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于、的恒等式为(
)
A.
B.
C.
D.
二、填空题
13.计算:_________.
14.若x2+mx+4可以写成一个(x+?)2的形式(问号“?”是一个数字),则m的值为________.
15.如图,点M是AB中点,点P在MB上,分别以AP,BP为边作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=6,ab=7,则图中阴影部分的面积为______.
16.如图,四个完全相同的长方形围一个大正方形,已知每个长方形的周长为60,面积为30,那么图中中间阴影部分的面积为___________.
17.已知,则代数式=_____________________
三、解答题
18.已知,,求下列各式的值
;
19.化简
(1)先化简,再求值:,其中.
(2)已知,,求的值.
20.如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)自主探究:如果用两种不同的方法表示图2中阴影部分的面积,从而发现一个等量关系是
;
(2)知识运用:若x﹣y=5,xy=6,则(x+y)2=
;
(3)知识迁移:设A=,B=x+2y﹣3,化简(A﹣B)2﹣(A+B)2的结果;
(4)知识延伸:若(2019﹣m)2+(m﹣2021)2=9,代数式(2019﹣m)(m﹣2021)=
.
参考答案
1.D
解:(a-2)2=a2-4a+4,
故选:D.
2.B
解:∵-8x=-2×4?x,
∴m=42=16,
解得m=16.
故选:B.
3.C
解:A、原式=a2-b2,所以A选项错误;
B、原式=-(a+b)(a-b)=-a2+b2,所以B选项错误;
C、原式=-n+n2,所以C选项正确;
D、原式=m2-2mn+n2,所以D选项错误.
故选:C.
4.D
解:∵,,,
∴
故选D.
5.C
解:
即整式的最小值为.
故选C.
6.A
解:,
.
故选A.
7.C
解:
故选择:C
8.C
解:∵
∴两边平方得:,
即:,
又∵,
∴,
∴
故选:C.
9.B
解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是、,可得:
,
将②化简得③,
由①得,将③代入可知.
故选:B.
10.A
解:设,
∴,
∴
=
=
=
=10000+1040
=11040
故选:A
11.B
解:①(x﹣1)(x+4)=x2+3x﹣4,不符合题意;
②(﹣3+x)(3+x)=x2﹣9,符合题意;
③(﹣5x+7y)(﹣5x﹣7y)=25x2﹣49y2,
符合题意;
④(xy﹣6)2=x2y2﹣12xy+36,符合题意;
⑤(﹣x﹣y)2=x2+2xy+y2,符合题意.
故选B.
12.C
解:图甲中图形的面积为:,
图乙中图形的面积为:,
∴,
故选:C.
13.4
解:,
故答案为:4.
14.±4
解:设问号“?”为n,
根据题意得:x2+mx+4=(x+n)2,
整理得:x2+mx+4=x2+2nx+n2,
∴m=2n,n2=4,
解得:n=±2,
∴m=2n=±4.
故答案为:±4.
15.13
解:,,.
.
故答案为:13.
16.780
解:设小长方形的长为a,宽为b,
则2(a+?b)=?60,?ab=?30,
a+b=?30,
图中阴影部分的面积
=(a+b)2-?4ab=?302-?4×30?=?780.
故答案为:780.
17.14
解:把,两边平方得:
故答案为:14.
18.(1)25;(2)37
解:(1)
(2)
19.(1),;(2)16.
解:(1)
=
,
当时,原式.
(2)
.
20.(1)(a
-
b)2=(a+b)2-4ab;(2)(x+y)2=49;(3)﹣x2+6x﹣9+4y2;(4)
解:(1)图2中的阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
图2的阴影部分也可以看作边长为(a+b)的大正方形面积减去4个长为a,宽为b的长方形的面积,即为(a+b)2﹣4ab,
所以有:(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(2)由(1)得(x+y)2=(x﹣y)2+4xy,
当x﹣y=5,xy=6,
则(x+y)2=52+4×6=49,
故答案为:49;
(3)∵A=,B=x+2y﹣3,
∴原式=A2﹣2AB+B2﹣(A2+2AB+B2)
=﹣4AB
=﹣4??(x+2y﹣3)
=﹣(x﹣3﹣2y)(x﹣3+2y)
=﹣[(x﹣3)2﹣(2y)2]
=﹣(x2﹣6x+9﹣4y2)
=﹣x2+6x﹣9+4y2;
(4)设A=2019﹣m,B=m﹣2021,
则A+B=2019﹣m+m﹣2021=﹣2,
A2+B2=9,
∵(A+B)2=A2+B2+2AB,
∴4=9+4AB,
∴AB=﹣,
即(2019﹣m)(m﹣2021)=﹣,
故答案为:﹣.
一、单选题
1.计算(a﹣2)2的结果是( )
A.a2﹣2a+4
B.a2+2a+4
C.a2﹣4a+2
D.a2﹣4a+4
2.如果二次三项式是一个完全平方式,那么m的值是(
)
A.
B.
C.4
D.
3.下列各式计算正确的是(
)
A.(a+b)(a-b)=a2+b2
B.(-a-b)(a-b)=a2-b2
C.(-n)2=-n+n2
D.(-m+n)2=m2+2mn+n2
4.已知,,,那么的值等于(
)
A.0
B.1
C.2
D.3
5.整式的最小值为(
)
A.
B.
C.
D.
6.比较与的大小,叙述正确的是(
)
A.
B.
C.由的大小确定
D.由的大小确定
7.将变形正确的是(
)
A.
B.
C.
D.
8.若,,则的值是(
)
A.-11
B.11
C.22
D.-22
9.有两个正方形A,B,现将B放在A的内部如图甲,若图甲和图乙中阴影部分面积分别为和,则正方形A,B的面积之和为( )
A.3
B.3.5
C.4
D.4.5
10.1921年伟大的中国共产党成立,2021年中国共产党迎来了百年华诞,若,则的值为(
)
A.11040
B.10520
C.8960
D.620
11.小明做了以下5道题:①(x﹣1)(x+4)=x2﹣4;②(﹣3+x)(3+x)=x2﹣9;③(﹣5x+7y)(﹣5x﹣7y)=25x2﹣49y2;④(xy﹣6)2=x2y2﹣12xy+36;⑤(﹣x﹣y)2=x2+2xy+y2,你认为小明一共做对了(
)
A.5道
B.4道
C.3道
D.2道
12.将图甲中明影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于、的恒等式为(
)
A.
B.
C.
D.
二、填空题
13.计算:_________.
14.若x2+mx+4可以写成一个(x+?)2的形式(问号“?”是一个数字),则m的值为________.
15.如图,点M是AB中点,点P在MB上,分别以AP,BP为边作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=6,ab=7,则图中阴影部分的面积为______.
16.如图,四个完全相同的长方形围一个大正方形,已知每个长方形的周长为60,面积为30,那么图中中间阴影部分的面积为___________.
17.已知,则代数式=_____________________
三、解答题
18.已知,,求下列各式的值
;
19.化简
(1)先化简,再求值:,其中.
(2)已知,,求的值.
20.如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)自主探究:如果用两种不同的方法表示图2中阴影部分的面积,从而发现一个等量关系是
;
(2)知识运用:若x﹣y=5,xy=6,则(x+y)2=
;
(3)知识迁移:设A=,B=x+2y﹣3,化简(A﹣B)2﹣(A+B)2的结果;
(4)知识延伸:若(2019﹣m)2+(m﹣2021)2=9,代数式(2019﹣m)(m﹣2021)=
.
参考答案
1.D
解:(a-2)2=a2-4a+4,
故选:D.
2.B
解:∵-8x=-2×4?x,
∴m=42=16,
解得m=16.
故选:B.
3.C
解:A、原式=a2-b2,所以A选项错误;
B、原式=-(a+b)(a-b)=-a2+b2,所以B选项错误;
C、原式=-n+n2,所以C选项正确;
D、原式=m2-2mn+n2,所以D选项错误.
故选:C.
4.D
解:∵,,,
∴
故选D.
5.C
解:
即整式的最小值为.
故选C.
6.A
解:,
.
故选A.
7.C
解:
故选择:C
8.C
解:∵
∴两边平方得:,
即:,
又∵,
∴,
∴
故选:C.
9.B
解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是、,可得:
,
将②化简得③,
由①得,将③代入可知.
故选:B.
10.A
解:设,
∴,
∴
=
=
=
=10000+1040
=11040
故选:A
11.B
解:①(x﹣1)(x+4)=x2+3x﹣4,不符合题意;
②(﹣3+x)(3+x)=x2﹣9,符合题意;
③(﹣5x+7y)(﹣5x﹣7y)=25x2﹣49y2,
符合题意;
④(xy﹣6)2=x2y2﹣12xy+36,符合题意;
⑤(﹣x﹣y)2=x2+2xy+y2,符合题意.
故选B.
12.C
解:图甲中图形的面积为:,
图乙中图形的面积为:,
∴,
故选:C.
13.4
解:,
故答案为:4.
14.±4
解:设问号“?”为n,
根据题意得:x2+mx+4=(x+n)2,
整理得:x2+mx+4=x2+2nx+n2,
∴m=2n,n2=4,
解得:n=±2,
∴m=2n=±4.
故答案为:±4.
15.13
解:,,.
.
故答案为:13.
16.780
解:设小长方形的长为a,宽为b,
则2(a+?b)=?60,?ab=?30,
a+b=?30,
图中阴影部分的面积
=(a+b)2-?4ab=?302-?4×30?=?780.
故答案为:780.
17.14
解:把,两边平方得:
故答案为:14.
18.(1)25;(2)37
解:(1)
(2)
19.(1),;(2)16.
解:(1)
=
,
当时,原式.
(2)
.
20.(1)(a
-
b)2=(a+b)2-4ab;(2)(x+y)2=49;(3)﹣x2+6x﹣9+4y2;(4)
解:(1)图2中的阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
图2的阴影部分也可以看作边长为(a+b)的大正方形面积减去4个长为a,宽为b的长方形的面积,即为(a+b)2﹣4ab,
所以有:(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(2)由(1)得(x+y)2=(x﹣y)2+4xy,
当x﹣y=5,xy=6,
则(x+y)2=52+4×6=49,
故答案为:49;
(3)∵A=,B=x+2y﹣3,
∴原式=A2﹣2AB+B2﹣(A2+2AB+B2)
=﹣4AB
=﹣4??(x+2y﹣3)
=﹣(x﹣3﹣2y)(x﹣3+2y)
=﹣[(x﹣3)2﹣(2y)2]
=﹣(x2﹣6x+9﹣4y2)
=﹣x2+6x﹣9+4y2;
(4)设A=2019﹣m,B=m﹣2021,
则A+B=2019﹣m+m﹣2021=﹣2,
A2+B2=9,
∵(A+B)2=A2+B2+2AB,
∴4=9+4AB,
∴AB=﹣,
即(2019﹣m)(m﹣2021)=﹣,
故答案为:﹣.
