五年级上册数学教案-★掷一掷 人教版(4)
文档属性
| 名称 | 五年级上册数学教案-★掷一掷 人教版(4) |  | |
| 格式 | zip | ||
| 文件大小 | 35.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 08:55:19 | ||
图片预览




文档简介
掷一掷
实验目的
1.
通过讨论、猜想、实验、验证的实验过程,巩固可能性的有关知识,知道同时掷两颗骰子出现的点数之和以及可能性情况,初步积累数学实验的活动经验。
2.
通过数学实验的过程,培养学生发现问题、提出问题、分析问题、解决问题的思维能力,加强学生的合作探究意识和动手实践能力。
3.
通过同时掷两颗骰子的实验,培养学生的随机思维,让学生学会用概率的眼光去观察生活,懂得看问题不绝对化,一切皆有可能。
4.
在统计过程中渗透用数据说话的科学精神;在实验过程中享受数学实验带来的快乐,体会数学的趣味性。
重点难点
重点:探索掷两颗骰子点数之和分别是2、3、4、5、6、7、8、9、10、11、12的可能性。
难点:让学生在数学实验中获得数学经验,用可能的眼光看世界,学会用数据说话。
实验准备
数学实验报告,骰子,PPT,平板电脑
课前准备:每两人为一组,每组有2颗骰子,一张数学实验报告、一台pad。
实验过程
一、直入主题,引出新课。
1.
一颗骰子。
出示:骰子动态图。
师:同学们,见过它吗?
生:骰子。
师:任意掷一颗骰子,向上的面可能是几?
生:1、2、3、4、5、6。
师:1、2、3、4、5、6出现的可能性怎么样?为什么?
生:可能性相等。
总结:骰子有六个面,每个面上的数字分别是1、2、3、4、5、6。无论怎么掷,都只有一个面向上,所以出现1、2、3、4、5、6的可能性相等。
2.
两颗骰子。
师:如果同时掷两颗骰子,结果会怎样呢?今天,我们就来探究两颗骰子相遇时会出现什么结果?(板书课题:两颗骰子的相遇)
二、初步猜想,开展实验。
1.
讨论1:同时掷两颗骰子,掷出的点数之和可能是(
)。
师:如果同时掷两颗骰子,把向上两个面的点数加起来,和可能是几呢?
生:2、3、4、5、6、7、8、9、10、11、12……
(生回答出现1,两颗骰子叠在一起。师说明,这是一个很少发生的事件,暂时不考虑。)
2.
讨论2:同时掷两颗骰子,掷出的点数之和最小是(
),最大是(
)。
师:同时掷两颗骰子,掷出的点数之和最小是多少,最大是多少呢?为什么?
生:2(一颗骰子最小掷到1,两颗骰子最小掷到1+1=2);12(一颗骰子最大掷到6,两颗骰子最大掷到6+6=12)
师:5有没有可能被掷到?8呢?2和12之间的数呢?
小结:同时掷两颗骰子,掷出的点数之和最小是2,最大是12;掷出的点数之和可能是2、3、4、5、6、7、8、9、10、11、12这11种情况。
3.
我猜想:点数之和是(
)的可能性比较大。
师:我们知道2、3、4、5、6、7、8、9、10、11、12这11个数都有可能出现,那这些数出现的可能性怎么样?(找三到四人回答。)
学生小组内讨论,填写猜想。
4.
实验探究点数之和出现的可能性。
师:我们学习数学大胆的猜想虽然重要,但最重要的还是要敢于实践,下面让我们一起开始骰子实验。看看实验结果是否和我们的猜想一样?
(1)确定实验工具:
师:需要什么实验工具?
生:骰子。
师:一颗够不够?要几颗?
生:两颗骰子。
(2)确定实验方法:
师:实验方法是什么?
生:掷骰子。
师:只是掷,行不行?
生:不行。掷骰子,记录点数之和。
师:掷一次,够不够?
生:不够,要掷很多次。
师总结:多次同时掷两颗骰子,记录出现次数。
(3)填写实验记录表:
点数之和
出现次数
(用画“正”字的方法记录)
出现次数
实验记录表第一行:表示点数之和的出现情况。点数之和从小到大填好2、3、4、5、6、7、8、9、10、11、12。
第二行:表示用画“正”字的方法记录点数之和出现的次数。
第三行:表示点数之和出现次数的汇总。
(4)实验建议:①同时掷两颗骰子,用画“正”字的方法记录。限时8分钟。
②一人负责掷,一人负责记录。
③全班鸦雀无声,专心实验。
我建议:掷的时候(拿起用手盖住的水杯),将水杯上下使劲晃动三次(师边说,边动手演示),然后看一下向上的点数之和是几,相应记录。
(5)开展实验。(计时器8分钟准备)
(6)实验结束,填写出现次数汇总和实验结果。部分同学汇报实验结果。
师:来汇报一下你们小组的实验结果。
(7)大数据汇总,分析交流。
师:我们的实验结果太丰富、太多了。看来,我们遇到了一个困难,通过不同的实验可以得到不同的实验结果。所以,准确地说,最终的实验结果只能说是“可能”出现这个最多,也“可能”出现那个最多,实验结果“不确定”。通过每个小组8分钟的实验,全班都没有得出统一的结果,我们应该怎样做呢?
生:把全班点数之和的出现次数合计一下,出现2的次数一共是多少,出现3的次数一共是多少,……,出现12的次数一共是多少,合计起来看哪一个数出现的次数最多,哪一个数出现的次数最少,就能得出结果了。
结论:当实验时间比较短、实验次数比较少的时候,偶然性就比较大。
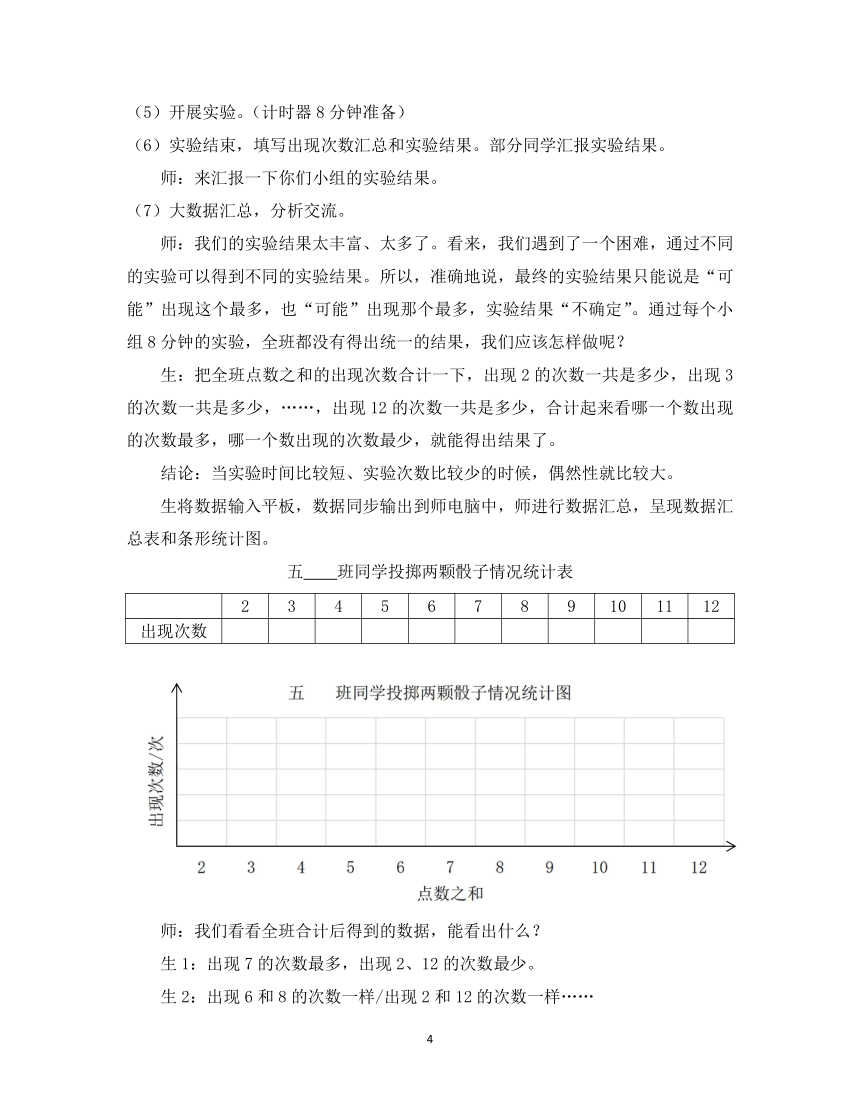
生将数据输入平板,数据同步输出到师电脑中,师进行数据汇总,呈现数据汇总表和条形统计图。
五
班同学投掷两颗骰子情况统计表
2
3
4
5
6
7
8
9
10
11
12
出现次数
师:我们看看全班合计后得到的数据,能看出什么?
生1:出现7的次数最多,出现2、12的次数最少。
生2:出现6和8的次数一样/出现2和12的次数一样……
总结:当实验的时间比较短、实验的次数比较少的时候,偶然性就比较大。实验的次数较多的时候,实验的结果就更接近真实,我们就能看出一定的规律。将全班的数据汇总,大数据量的统计,让实验的结果更加具有真实性、更有研究的价值。
三、验证猜想,经历数学化。
谈话:虽说实践是检验真理的唯一标准,但今天我们发现“眼见未必真实”“实验结果未必正确”,这是为什么呢?咱们一起来思考,一起推理推理。
1.
填写表格1。
(1)“2”的组成
师:首先来看2。怎样掷两颗骰子才能出现2呢?
生:1+1。
师:有没有其他的方法?
生:没有了。
小结:要掷出2,两颗骰子只能都是1的那一面向上。只有一种方法。
(2)“3”的组成
师:再来看3,怎样才能让点数之和出现3呢?
生:一颗骰子出现1,一颗骰子出现2。(1+2)
师:如果老师手里有一颗红骰子和一颗蓝骰子,现在红骰子出现1、蓝骰子出现2,点数之和是3;那有没有可能红骰子出现2,蓝骰子出现1呢?点数之和也是3。这两种情况是一种吗?
生:不是。
师:就用1+2和2+1的方式呈现。
(3)“4”的组成
师:4呢?(4=1+3=2+2=3+1)
(4)“8”的组成
师:8呢?
生:1+7、2+6……
师:1+7对吗?为什么?(如学生没有出现1+7,师问:为什么不是1+7?)
生:不对。骰子上的点数只有1、2、3、4、5、6,不可能掷到7。
师:所以8的组成只能是2+6、3+5、4+4、5+3、6+2。
(5)“9”的组成
生:3+6、4+5、5+4、6+3。
师:为什么不能是1+8?2+7?
生:骰子上没有7和8这两个点数。
(6)“10”“11”“12”的组成。
……
学生汇报,完善表格。
点数之和
2
3
4
5
6
7
8
9
10
11
12
组合方式
1+1
1+2
2+1
1+3
2+2
3+1
1+4
2+3
3+2
4+1
1+5
2+4
3+3
4+2
5+1
1+6
2+5
3+4
4+3
5+2
6+1
2+6
3+5
4+4
5+3
6+2
3+6
4+5
5+4
6+3
4+6
5+5
6+4
5+6
6+5
6+6
组合数
1
2
3
4
5
6
5
4
3
2
1
2.
验证猜想:
谈话:同学们,回顾实验前的猜想,结合实验的结论,通过刚才的思考和推理,你发现了什么?心中还有什么疑问?
现在我们发现:为什么出现6、7、8的次数较多,出现2、12的次数较少了吗?
生:因为7的组合方式最多,组合数最大,所以出现7的次数比较多;而2和12的组合方式最少,组合数最小,出现2和12的次数比较少。
师:从表格中,可以看出出现2的方法只有一种(1+1),出现3的方法有两种(1+2和2+1)……出现7的方法有六种(1+6=2+5=3+4=4+3=5+2=6+1)……出现12的方法只有一种(6+6)。所以,出现7的次数最多,出现2、12的次数最少,出现6和8、5和9、4和10、3和11、2和12的次数相等。
3.
呈现表格2。
师:老师有一个想法,我们来看,第一行这边都是1+几,到这里变成了2+6,能不能把2+6挪个位置,让它变得更有序些?
生:把2+6挪到下面一行,这样下面一行就都变成了2+几。
同理:3+几,4+几,5+几,6+几。
点数之和
2
3
4
5
6
7
8
9
10
11
12
组合方式
1+1
1+2
2+1
1+3
2+2
3+1
1+4
2+3
3+2
4+1
1+5
2+4
3+3
4+2
5+1
1+6
2+5
3+4
4+3
5+2
6+1
2+6
3+5
4+4
5+3
6+2
3+6
4+5
5+4
6+3
4+6
5+5
6+4
5+6
6+5
6+6
组合数
1
2
3
4
5
6
5
4
3
2
1
4.
再次梳理表格,体现简洁和有序。
谈话:同学们,从表格1到表格2,经历了实验到理论的探索历程,你们真了不起!不过,还有更加简洁的呈现方式,我们一起来研究,好吗?
(1)1和1、2、3、4、5、6
师:看看这几个1有没有共同点呢?(用红色圆圈圈出来)能不能把它们都看作是红色骰子掷出来的1,而这些1、2、3、4、5、6看作是蓝色骰子掷出来的呢?可以。如果用这样的表格呢?这里的1表示红色骰子掷到的1,第一行的1、2、3、4、5、6表示蓝色骰子掷到的数。中间的这些格子表示它们一一对应的和。1+1、1+2、1+3、1+4、1+5、1+6。
1
2
3
4
5
6
1
1+1
1+2
1+3
1+4
1+5
1+6
师:然后,1+1=2,1+2=3,1+3=4,1+4=5,1+5=6,1+6=7。
1
2
3
4
5
6
1
2
3
4
5
6
7
(2)
2和1、2、3、4、5、6
师:同理,第二行是否也可以这样呢?这个2表示红色骰子掷到的2,第一行的1、2、3、4、5、6表示蓝色骰子掷到的数。中间的这些格子表示它们一一对应的和。
1
2
3
4
5
6
2
3
4
5
6
7
8
(3)
1、2和1、2、3、4、5、6
师:老师觉得这两张表格还有些繁琐,你有什么更好的方法吗?
生:这两张表格第一行是一样的,可以做一下汇总。
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
(4)
3、4、5、6和1、2、3、4、5、6
师:这里蓝色骰子能掷到1、2、3、4、5、6,红色骰子只能掷到1和2,可能吗?红色骰子还可能掷到?
生:3。(同步ppt出现)
师:结果是?
生:4、5、6、7、8、9。
师:同样的道理,红色骰子还可能掷到4、5、6。把这些点数都加进来,就可以形成这样一张表格:最上面一行表示的是蓝色骰子的点数,最左边一列表示的是红色骰子的点数,中间的各个数据表示掷得的两个骰子之和。
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
师:这个表格比刚才那张简单多了吧?
生:是的。
师:如果把红色骰子和蓝色骰子掷到的点数隐去,那点数之和是不是更清楚了?
生:是的。
师:如果给相同的数字标上相同的颜色呢?
生:更清楚了。
师:点数之和出现什么的可能性最大?出现什么的可能性最小?出现什么和什么的可能性相等呢?
四、总结反思,出乎意料。
1.
总结反思。
(1)撰写反思
同学们,咱们从实验前的猜想开始,经历了实验、数据汇总,并进行反复思考,现在心中有什么想法?有什么心得体会和感想感触?拿起你的神奇笔,写出你的总结或反思吧。(PPT播放轻音乐)
同伴分享
分享是最高阶的学习!让我们一起来分享同学们的学习、思考的成果吧!
意料之外,情理之中。
数学课堂也可以是这样的:讨论、猜想、实验、结论、反思,数学学习也可以是这样的:“实践出真理”也会有片面性,“理论来提升”是理想化的世界。今天的学习,让我们发现“一切皆有可能”的数学世界!
实验目的
1.
通过讨论、猜想、实验、验证的实验过程,巩固可能性的有关知识,知道同时掷两颗骰子出现的点数之和以及可能性情况,初步积累数学实验的活动经验。
2.
通过数学实验的过程,培养学生发现问题、提出问题、分析问题、解决问题的思维能力,加强学生的合作探究意识和动手实践能力。
3.
通过同时掷两颗骰子的实验,培养学生的随机思维,让学生学会用概率的眼光去观察生活,懂得看问题不绝对化,一切皆有可能。
4.
在统计过程中渗透用数据说话的科学精神;在实验过程中享受数学实验带来的快乐,体会数学的趣味性。
重点难点
重点:探索掷两颗骰子点数之和分别是2、3、4、5、6、7、8、9、10、11、12的可能性。
难点:让学生在数学实验中获得数学经验,用可能的眼光看世界,学会用数据说话。
实验准备
数学实验报告,骰子,PPT,平板电脑
课前准备:每两人为一组,每组有2颗骰子,一张数学实验报告、一台pad。
实验过程
一、直入主题,引出新课。
1.
一颗骰子。
出示:骰子动态图。
师:同学们,见过它吗?
生:骰子。
师:任意掷一颗骰子,向上的面可能是几?
生:1、2、3、4、5、6。
师:1、2、3、4、5、6出现的可能性怎么样?为什么?
生:可能性相等。
总结:骰子有六个面,每个面上的数字分别是1、2、3、4、5、6。无论怎么掷,都只有一个面向上,所以出现1、2、3、4、5、6的可能性相等。
2.
两颗骰子。
师:如果同时掷两颗骰子,结果会怎样呢?今天,我们就来探究两颗骰子相遇时会出现什么结果?(板书课题:两颗骰子的相遇)
二、初步猜想,开展实验。
1.
讨论1:同时掷两颗骰子,掷出的点数之和可能是(
)。
师:如果同时掷两颗骰子,把向上两个面的点数加起来,和可能是几呢?
生:2、3、4、5、6、7、8、9、10、11、12……
(生回答出现1,两颗骰子叠在一起。师说明,这是一个很少发生的事件,暂时不考虑。)
2.
讨论2:同时掷两颗骰子,掷出的点数之和最小是(
),最大是(
)。
师:同时掷两颗骰子,掷出的点数之和最小是多少,最大是多少呢?为什么?
生:2(一颗骰子最小掷到1,两颗骰子最小掷到1+1=2);12(一颗骰子最大掷到6,两颗骰子最大掷到6+6=12)
师:5有没有可能被掷到?8呢?2和12之间的数呢?
小结:同时掷两颗骰子,掷出的点数之和最小是2,最大是12;掷出的点数之和可能是2、3、4、5、6、7、8、9、10、11、12这11种情况。
3.
我猜想:点数之和是(
)的可能性比较大。
师:我们知道2、3、4、5、6、7、8、9、10、11、12这11个数都有可能出现,那这些数出现的可能性怎么样?(找三到四人回答。)
学生小组内讨论,填写猜想。
4.
实验探究点数之和出现的可能性。
师:我们学习数学大胆的猜想虽然重要,但最重要的还是要敢于实践,下面让我们一起开始骰子实验。看看实验结果是否和我们的猜想一样?
(1)确定实验工具:
师:需要什么实验工具?
生:骰子。
师:一颗够不够?要几颗?
生:两颗骰子。
(2)确定实验方法:
师:实验方法是什么?
生:掷骰子。
师:只是掷,行不行?
生:不行。掷骰子,记录点数之和。
师:掷一次,够不够?
生:不够,要掷很多次。
师总结:多次同时掷两颗骰子,记录出现次数。
(3)填写实验记录表:
点数之和
出现次数
(用画“正”字的方法记录)
出现次数
实验记录表第一行:表示点数之和的出现情况。点数之和从小到大填好2、3、4、5、6、7、8、9、10、11、12。
第二行:表示用画“正”字的方法记录点数之和出现的次数。
第三行:表示点数之和出现次数的汇总。
(4)实验建议:①同时掷两颗骰子,用画“正”字的方法记录。限时8分钟。
②一人负责掷,一人负责记录。
③全班鸦雀无声,专心实验。
我建议:掷的时候(拿起用手盖住的水杯),将水杯上下使劲晃动三次(师边说,边动手演示),然后看一下向上的点数之和是几,相应记录。
(5)开展实验。(计时器8分钟准备)
(6)实验结束,填写出现次数汇总和实验结果。部分同学汇报实验结果。
师:来汇报一下你们小组的实验结果。
(7)大数据汇总,分析交流。
师:我们的实验结果太丰富、太多了。看来,我们遇到了一个困难,通过不同的实验可以得到不同的实验结果。所以,准确地说,最终的实验结果只能说是“可能”出现这个最多,也“可能”出现那个最多,实验结果“不确定”。通过每个小组8分钟的实验,全班都没有得出统一的结果,我们应该怎样做呢?
生:把全班点数之和的出现次数合计一下,出现2的次数一共是多少,出现3的次数一共是多少,……,出现12的次数一共是多少,合计起来看哪一个数出现的次数最多,哪一个数出现的次数最少,就能得出结果了。
结论:当实验时间比较短、实验次数比较少的时候,偶然性就比较大。
生将数据输入平板,数据同步输出到师电脑中,师进行数据汇总,呈现数据汇总表和条形统计图。
五
班同学投掷两颗骰子情况统计表
2
3
4
5
6
7
8
9
10
11
12
出现次数
师:我们看看全班合计后得到的数据,能看出什么?
生1:出现7的次数最多,出现2、12的次数最少。
生2:出现6和8的次数一样/出现2和12的次数一样……
总结:当实验的时间比较短、实验的次数比较少的时候,偶然性就比较大。实验的次数较多的时候,实验的结果就更接近真实,我们就能看出一定的规律。将全班的数据汇总,大数据量的统计,让实验的结果更加具有真实性、更有研究的价值。
三、验证猜想,经历数学化。
谈话:虽说实践是检验真理的唯一标准,但今天我们发现“眼见未必真实”“实验结果未必正确”,这是为什么呢?咱们一起来思考,一起推理推理。
1.
填写表格1。
(1)“2”的组成
师:首先来看2。怎样掷两颗骰子才能出现2呢?
生:1+1。
师:有没有其他的方法?
生:没有了。
小结:要掷出2,两颗骰子只能都是1的那一面向上。只有一种方法。
(2)“3”的组成
师:再来看3,怎样才能让点数之和出现3呢?
生:一颗骰子出现1,一颗骰子出现2。(1+2)
师:如果老师手里有一颗红骰子和一颗蓝骰子,现在红骰子出现1、蓝骰子出现2,点数之和是3;那有没有可能红骰子出现2,蓝骰子出现1呢?点数之和也是3。这两种情况是一种吗?
生:不是。
师:就用1+2和2+1的方式呈现。
(3)“4”的组成
师:4呢?(4=1+3=2+2=3+1)
(4)“8”的组成
师:8呢?
生:1+7、2+6……
师:1+7对吗?为什么?(如学生没有出现1+7,师问:为什么不是1+7?)
生:不对。骰子上的点数只有1、2、3、4、5、6,不可能掷到7。
师:所以8的组成只能是2+6、3+5、4+4、5+3、6+2。
(5)“9”的组成
生:3+6、4+5、5+4、6+3。
师:为什么不能是1+8?2+7?
生:骰子上没有7和8这两个点数。
(6)“10”“11”“12”的组成。
……
学生汇报,完善表格。
点数之和
2
3
4
5
6
7
8
9
10
11
12
组合方式
1+1
1+2
2+1
1+3
2+2
3+1
1+4
2+3
3+2
4+1
1+5
2+4
3+3
4+2
5+1
1+6
2+5
3+4
4+3
5+2
6+1
2+6
3+5
4+4
5+3
6+2
3+6
4+5
5+4
6+3
4+6
5+5
6+4
5+6
6+5
6+6
组合数
1
2
3
4
5
6
5
4
3
2
1
2.
验证猜想:
谈话:同学们,回顾实验前的猜想,结合实验的结论,通过刚才的思考和推理,你发现了什么?心中还有什么疑问?
现在我们发现:为什么出现6、7、8的次数较多,出现2、12的次数较少了吗?
生:因为7的组合方式最多,组合数最大,所以出现7的次数比较多;而2和12的组合方式最少,组合数最小,出现2和12的次数比较少。
师:从表格中,可以看出出现2的方法只有一种(1+1),出现3的方法有两种(1+2和2+1)……出现7的方法有六种(1+6=2+5=3+4=4+3=5+2=6+1)……出现12的方法只有一种(6+6)。所以,出现7的次数最多,出现2、12的次数最少,出现6和8、5和9、4和10、3和11、2和12的次数相等。
3.
呈现表格2。
师:老师有一个想法,我们来看,第一行这边都是1+几,到这里变成了2+6,能不能把2+6挪个位置,让它变得更有序些?
生:把2+6挪到下面一行,这样下面一行就都变成了2+几。
同理:3+几,4+几,5+几,6+几。
点数之和
2
3
4
5
6
7
8
9
10
11
12
组合方式
1+1
1+2
2+1
1+3
2+2
3+1
1+4
2+3
3+2
4+1
1+5
2+4
3+3
4+2
5+1
1+6
2+5
3+4
4+3
5+2
6+1
2+6
3+5
4+4
5+3
6+2
3+6
4+5
5+4
6+3
4+6
5+5
6+4
5+6
6+5
6+6
组合数
1
2
3
4
5
6
5
4
3
2
1
4.
再次梳理表格,体现简洁和有序。
谈话:同学们,从表格1到表格2,经历了实验到理论的探索历程,你们真了不起!不过,还有更加简洁的呈现方式,我们一起来研究,好吗?
(1)1和1、2、3、4、5、6
师:看看这几个1有没有共同点呢?(用红色圆圈圈出来)能不能把它们都看作是红色骰子掷出来的1,而这些1、2、3、4、5、6看作是蓝色骰子掷出来的呢?可以。如果用这样的表格呢?这里的1表示红色骰子掷到的1,第一行的1、2、3、4、5、6表示蓝色骰子掷到的数。中间的这些格子表示它们一一对应的和。1+1、1+2、1+3、1+4、1+5、1+6。
1
2
3
4
5
6
1
1+1
1+2
1+3
1+4
1+5
1+6
师:然后,1+1=2,1+2=3,1+3=4,1+4=5,1+5=6,1+6=7。
1
2
3
4
5
6
1
2
3
4
5
6
7
(2)
2和1、2、3、4、5、6
师:同理,第二行是否也可以这样呢?这个2表示红色骰子掷到的2,第一行的1、2、3、4、5、6表示蓝色骰子掷到的数。中间的这些格子表示它们一一对应的和。
1
2
3
4
5
6
2
3
4
5
6
7
8
(3)
1、2和1、2、3、4、5、6
师:老师觉得这两张表格还有些繁琐,你有什么更好的方法吗?
生:这两张表格第一行是一样的,可以做一下汇总。
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
(4)
3、4、5、6和1、2、3、4、5、6
师:这里蓝色骰子能掷到1、2、3、4、5、6,红色骰子只能掷到1和2,可能吗?红色骰子还可能掷到?
生:3。(同步ppt出现)
师:结果是?
生:4、5、6、7、8、9。
师:同样的道理,红色骰子还可能掷到4、5、6。把这些点数都加进来,就可以形成这样一张表格:最上面一行表示的是蓝色骰子的点数,最左边一列表示的是红色骰子的点数,中间的各个数据表示掷得的两个骰子之和。
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
师:这个表格比刚才那张简单多了吧?
生:是的。
师:如果把红色骰子和蓝色骰子掷到的点数隐去,那点数之和是不是更清楚了?
生:是的。
师:如果给相同的数字标上相同的颜色呢?
生:更清楚了。
师:点数之和出现什么的可能性最大?出现什么的可能性最小?出现什么和什么的可能性相等呢?
四、总结反思,出乎意料。
1.
总结反思。
(1)撰写反思
同学们,咱们从实验前的猜想开始,经历了实验、数据汇总,并进行反复思考,现在心中有什么想法?有什么心得体会和感想感触?拿起你的神奇笔,写出你的总结或反思吧。(PPT播放轻音乐)
同伴分享
分享是最高阶的学习!让我们一起来分享同学们的学习、思考的成果吧!
意料之外,情理之中。
数学课堂也可以是这样的:讨论、猜想、实验、结论、反思,数学学习也可以是这样的:“实践出真理”也会有片面性,“理论来提升”是理想化的世界。今天的学习,让我们发现“一切皆有可能”的数学世界!
