【人教九上数学学霸听课笔记】23.1 图形的旋转 第2课时 旋转作图 课件(共21张PPT)
文档属性
| 名称 | 【人教九上数学学霸听课笔记】23.1 图形的旋转 第2课时 旋转作图 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-18 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第2课时 旋转作图
探究与应用
随堂小检测
第二十三章 旋转
目标一 会分析基本图案的旋转
探究
以图23-1-12为基本图形进行旋转构图,当旋转中心与旋转角不同的时候,旋转后产生的图案一样吗?观察下列操作,并填空.
图23-1-12
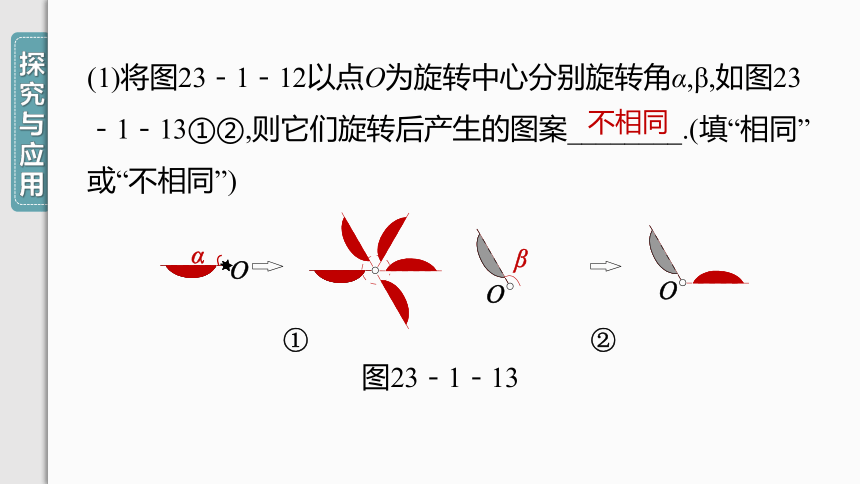
(1)将图23-1-12以点O为旋转中心分别旋转角α,β,如图23-1-13①②,则它们旋转后产生的图案________.(填“相同”或“不相同”)
图23-1-13
不相同
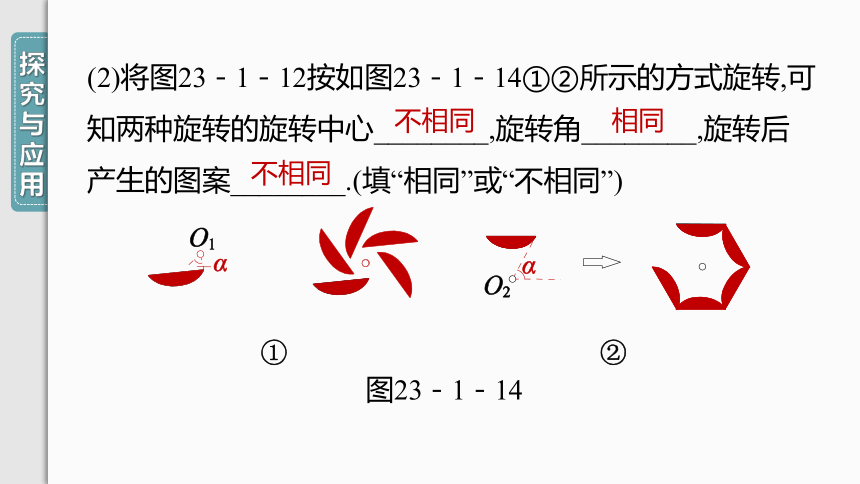
(2)将图23-1-12按如图23-1-14①②所示的方式旋转,可知两种旋转的旋转中心________,旋转角________,旋转后产生的图案________.(填“相同”或“不相同”)
图23-1-14
不相同
相同
不相同
归纳
决定基本图形旋转后的图案效果的因素
将一个基本图形旋转,产生的图案效果跟____________和
____________有关.
旋转中心
旋转角度
例1
如图23-1-15是一个风车的轮廓,它可以看作是一个风叶经过几次旋转得到的?每次旋转了多少度?这个风车的形成还有哪些旋转方式?
图23-1-15
[解析]
寻找“基本图案”,可以把一个风叶作为“基本图案”,还可以把几个风叶为一组作为“基本图案”.
解:它可以看作是一个风叶经过五次旋转得到的,每次旋转了60°.还可以把连续的两个或三个或相对的两个风叶看成一个“基本图案”,分别经过两次或一次或两次旋转得到,每次的旋转角度分别为120°或180°或60°.
目标二 会旋转作图
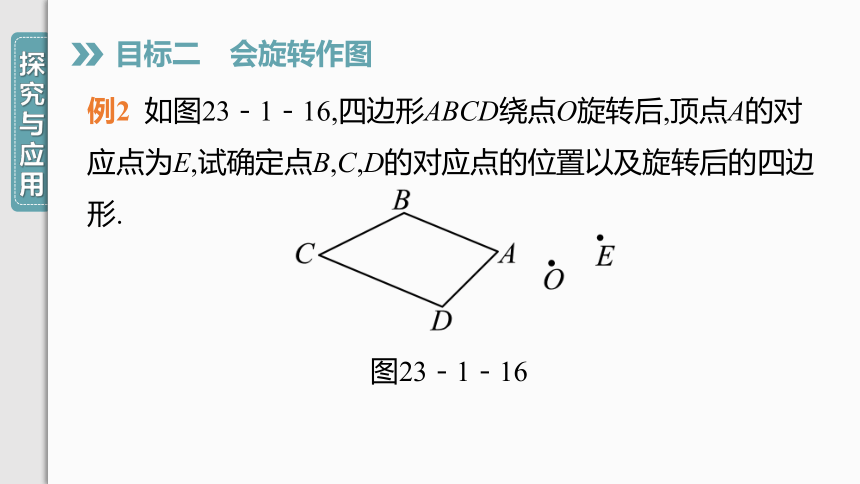
例2
如图23-1-16,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置以及旋转后的四边形.
图23-1-16
[解析]
连接OA,OE,OB,OC,OD,顺时针方向作∠BOF=∠AOE,且使OF=OB,则点F为点B的对应点,利用同样的方法作出点C的对应点G,点D的对应点H,于是得到旋转后的四边形EFGH.
解:如图,点B,C,D的对应点分别为F,G,H,四边形EFGH为所作.
例3
如图23-1-17,正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.
(1)画出△OAB关于y轴对称的△OA1B1,
并写出点A1的坐标;
(2)画出△OAB绕原点O顺时针旋转90°
后得到的△OA2B2,并写出点A2的坐标.
图23-1-17
解:(1)△OA1B1如图所示,A1(-4,1).
(2)△OA2B2如图所示,A2(1,-4).
归纳
作旋转图形的一般步骤
一连:连接已知图形上的关键点与旋转中心;
二定:确定旋转的方向和旋转的角度;
三画:画出旋转角;
归纳
四截:在旋转角的另一条边上截取一点,使其到旋转中心的
距离等于所取关键点到旋转中心的距离,得到关键点的对应
点;
五连:顺次连接所得的对应点,从而作出旋转后的图形.
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是
( )
图23-1-18
D
2.如图23-1-19,P是等边三角形ABC内的一点,以点A为旋转中心,把△PAC逆时针旋转60°,画出旋转后的图形.
解:如图,△P′AB即为所画的三角形.
图23-1-19
3.如图23-1-20,正方形网格中,每个小正方形的边长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点A(5,2),
B(5,5),C(1,1)均在格点上.
(1)画出将△ABC向左平移5个单位长度
得到的△A1B1C1,并写出点A1的坐标;
(2)画出△A1B1C1绕点C1顺时针旋转90°后
得到的△A2B2C1,并写出点A2的坐标.
图23-1-20
解:(1)如图所示,△A1B1C1即为所求,点A1的坐标为(0,2).
(2)如图所示,△A2B2C1即为所求,点A2的坐标为(-3,-3).
https://www.21cnjy.com/help/help_extract.php
第2课时 旋转作图
探究与应用
随堂小检测
第二十三章 旋转
目标一 会分析基本图案的旋转
探究
以图23-1-12为基本图形进行旋转构图,当旋转中心与旋转角不同的时候,旋转后产生的图案一样吗?观察下列操作,并填空.
图23-1-12
(1)将图23-1-12以点O为旋转中心分别旋转角α,β,如图23-1-13①②,则它们旋转后产生的图案________.(填“相同”或“不相同”)
图23-1-13
不相同
(2)将图23-1-12按如图23-1-14①②所示的方式旋转,可知两种旋转的旋转中心________,旋转角________,旋转后产生的图案________.(填“相同”或“不相同”)
图23-1-14
不相同
相同
不相同
归纳
决定基本图形旋转后的图案效果的因素
将一个基本图形旋转,产生的图案效果跟____________和
____________有关.
旋转中心
旋转角度
例1
如图23-1-15是一个风车的轮廓,它可以看作是一个风叶经过几次旋转得到的?每次旋转了多少度?这个风车的形成还有哪些旋转方式?
图23-1-15
[解析]
寻找“基本图案”,可以把一个风叶作为“基本图案”,还可以把几个风叶为一组作为“基本图案”.
解:它可以看作是一个风叶经过五次旋转得到的,每次旋转了60°.还可以把连续的两个或三个或相对的两个风叶看成一个“基本图案”,分别经过两次或一次或两次旋转得到,每次的旋转角度分别为120°或180°或60°.
目标二 会旋转作图
例2
如图23-1-16,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置以及旋转后的四边形.
图23-1-16
[解析]
连接OA,OE,OB,OC,OD,顺时针方向作∠BOF=∠AOE,且使OF=OB,则点F为点B的对应点,利用同样的方法作出点C的对应点G,点D的对应点H,于是得到旋转后的四边形EFGH.
解:如图,点B,C,D的对应点分别为F,G,H,四边形EFGH为所作.
例3
如图23-1-17,正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.
(1)画出△OAB关于y轴对称的△OA1B1,
并写出点A1的坐标;
(2)画出△OAB绕原点O顺时针旋转90°
后得到的△OA2B2,并写出点A2的坐标.
图23-1-17
解:(1)△OA1B1如图所示,A1(-4,1).
(2)△OA2B2如图所示,A2(1,-4).
归纳
作旋转图形的一般步骤
一连:连接已知图形上的关键点与旋转中心;
二定:确定旋转的方向和旋转的角度;
三画:画出旋转角;
归纳
四截:在旋转角的另一条边上截取一点,使其到旋转中心的
距离等于所取关键点到旋转中心的距离,得到关键点的对应
点;
五连:顺次连接所得的对应点,从而作出旋转后的图形.
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是
( )
图23-1-18
D
2.如图23-1-19,P是等边三角形ABC内的一点,以点A为旋转中心,把△PAC逆时针旋转60°,画出旋转后的图形.
解:如图,△P′AB即为所画的三角形.
图23-1-19
3.如图23-1-20,正方形网格中,每个小正方形的边长都是1个单位长度.在平面直角坐标系中,△ABC的三个顶点A(5,2),
B(5,5),C(1,1)均在格点上.
(1)画出将△ABC向左平移5个单位长度
得到的△A1B1C1,并写出点A1的坐标;
(2)画出△A1B1C1绕点C1顺时针旋转90°后
得到的△A2B2C1,并写出点A2的坐标.
图23-1-20
解:(1)如图所示,△A1B1C1即为所求,点A1的坐标为(0,2).
(2)如图所示,△A2B2C1即为所求,点A2的坐标为(-3,-3).
https://www.21cnjy.com/help/help_extract.php
同课章节目录
